n Find the distance between points A1 4

n Find the distance between points A(1, 4) and B(-3, 9)

Objective n SW recall area and perimeter formulas so that they can find the area and perimeter of irregular regions.

Compare: n Regular polygons vs. polygons

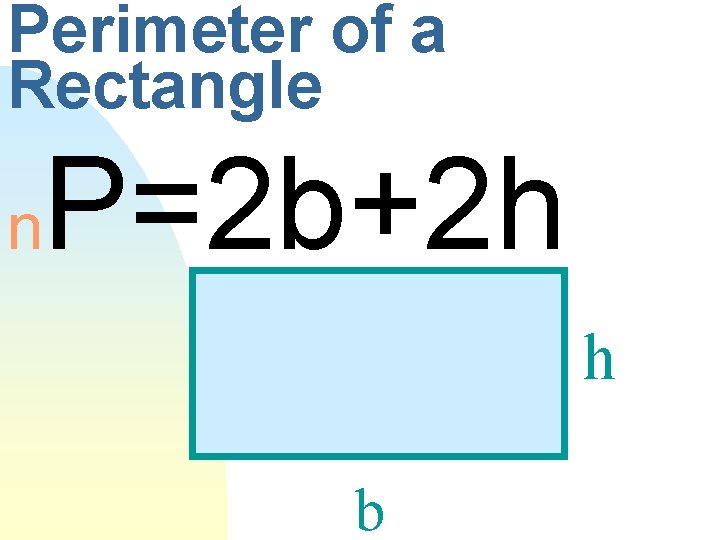
Perimeter of a Rectangle n P=2 b+2 h h b

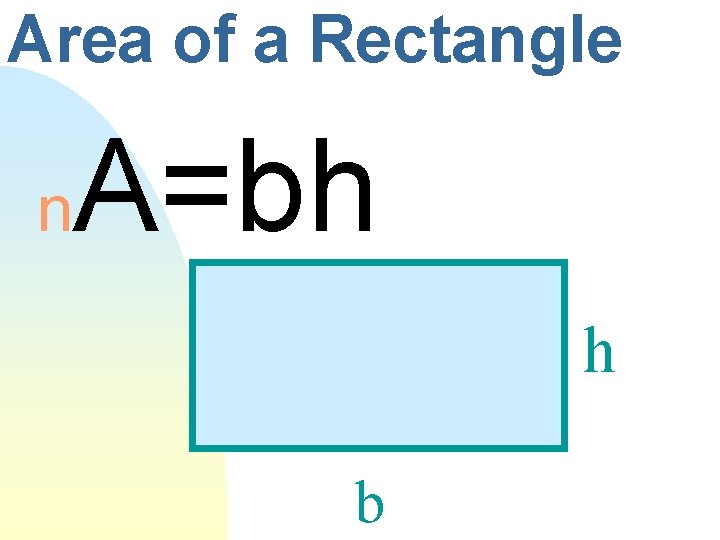
Area of a Rectangle n A=bh h b

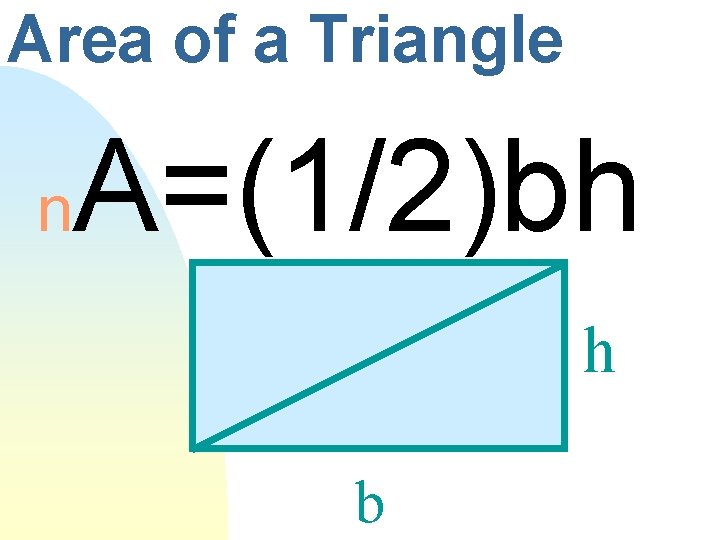
Area of a Triangle n A=(1/2)bh h b

Irregular Region n A region(shape) composed of many smaller regions(shapes)

Area of an Irregular Region n The sum of the areas of all the nonoverlapping parts of the region

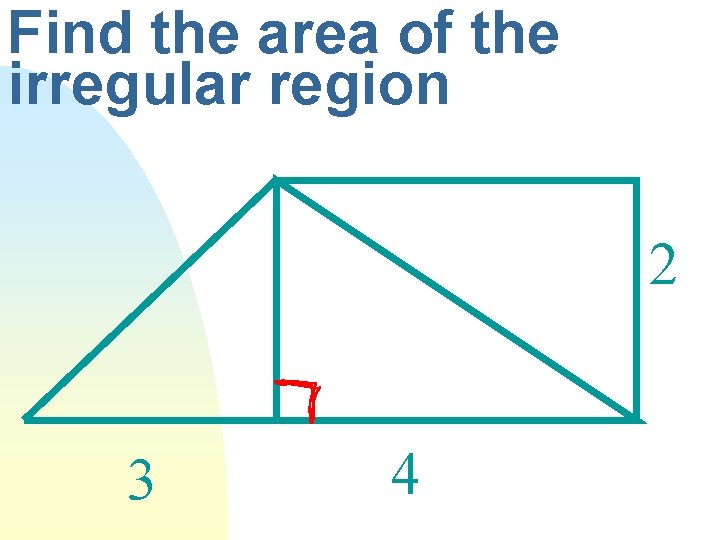
Find the area of the irregular region 2 3 4

Perimeter of an Irregular Region n The distance around the region.

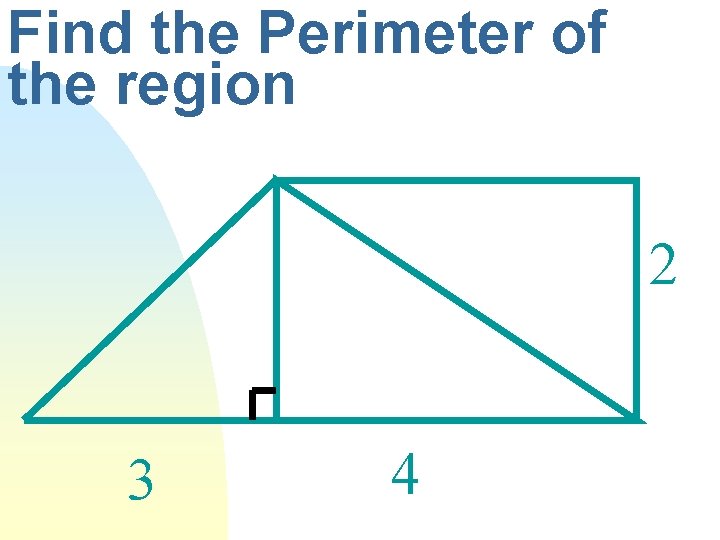
Find the Perimeter of the region 2 3 4

Conclusions n 1) To find the area of an irregular region, find the areas of its smaller _____ and find their _____.

Conclusions n 1) To find the area of an irregular region, find the areas of its smaller parts and find their _____. sum

Conclusions n 2) To find the perimeter of an irregular region, find the ____ around the region.

Conclusions n 2) To find the perimeter of an irregular region, find the ____ distance around the region.

CW/HW n Practice 5 -1 odd problems

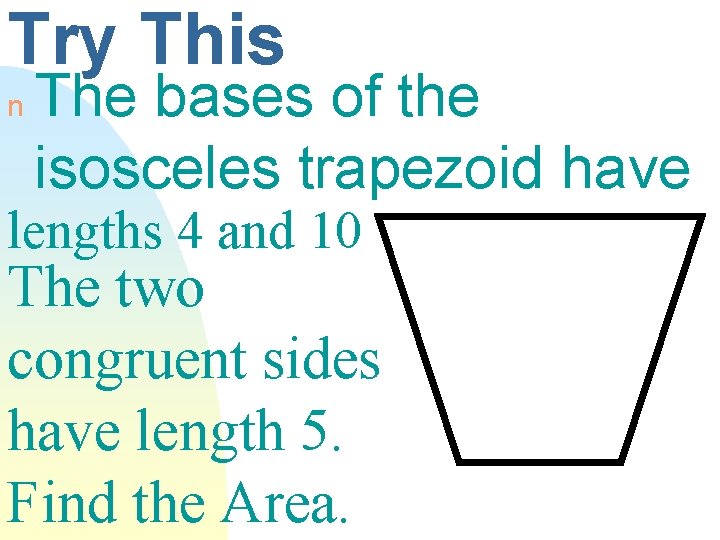
Try This n The bases of the isosceles trapezoid have lengths 4 and 10 The two congruent sides have length 5. Find the Area.

Objective n SW define and apply the Pythagorean Theorem so that they can find the dimensions of geometric figures.

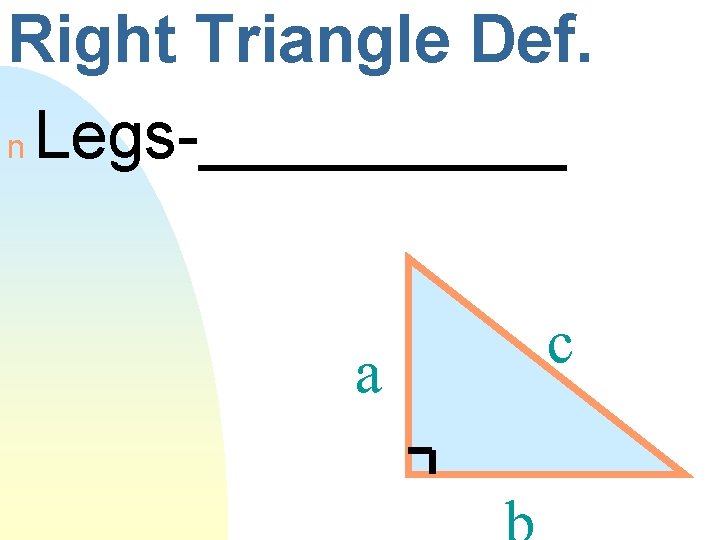
Right Triangle Def. n Legs-_____ a c

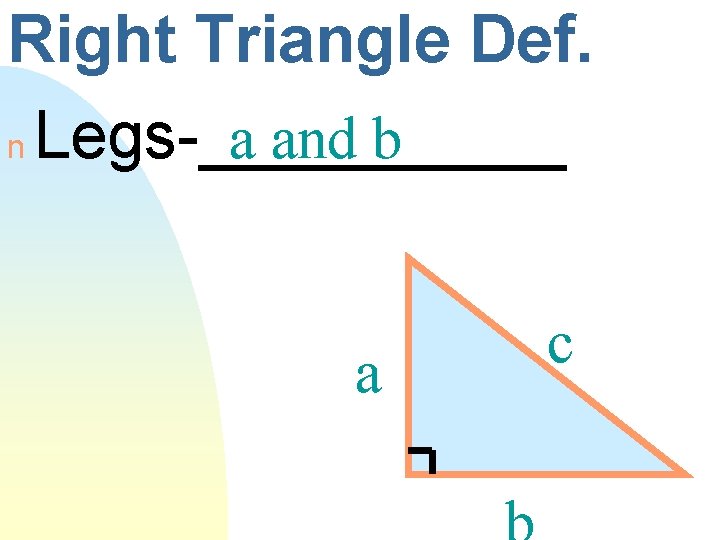
Right Triangle Def. a and b n Legs-_____ a c

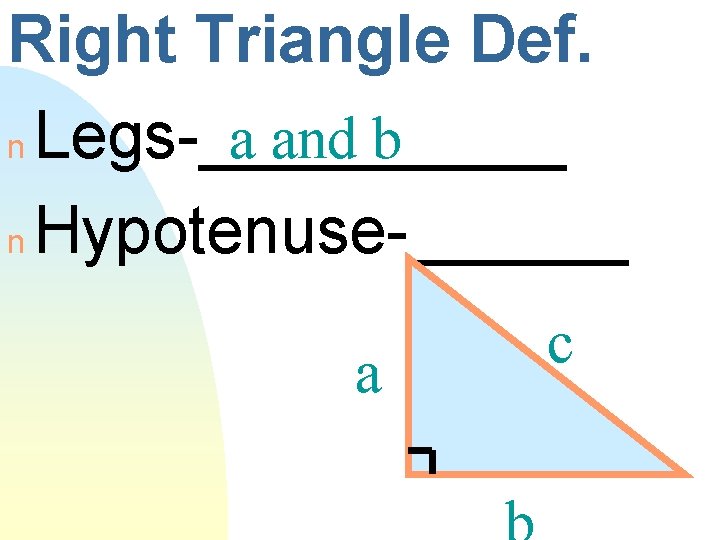
Right Triangle Def. a and b n Legs-_____ n Hypotenuse-______ a c

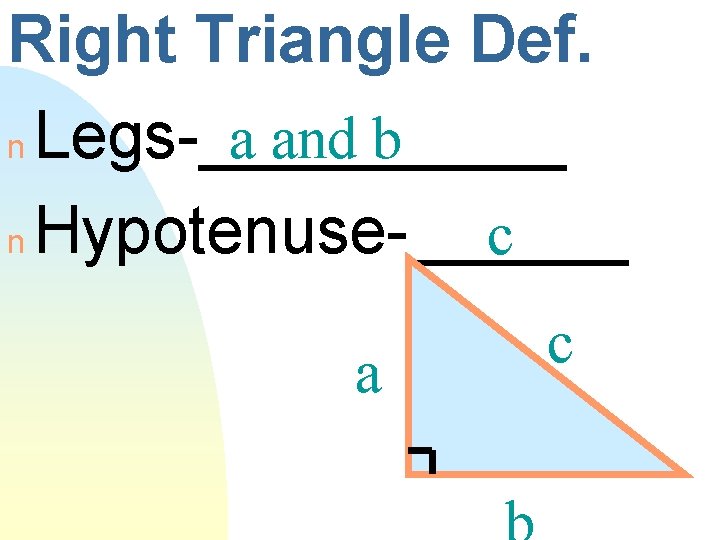
Right Triangle Def. a and b n Legs-_____ n Hypotenuse-______ c a c

Hypotenuse n The ____ side of a right triangle across from the ____ angle.

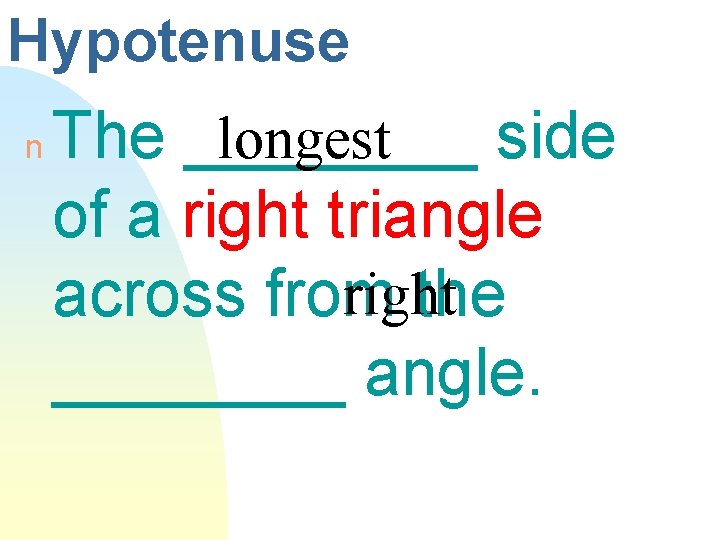
Hypotenuse n longest The ____ side of a right triangle right across from the ____ angle.

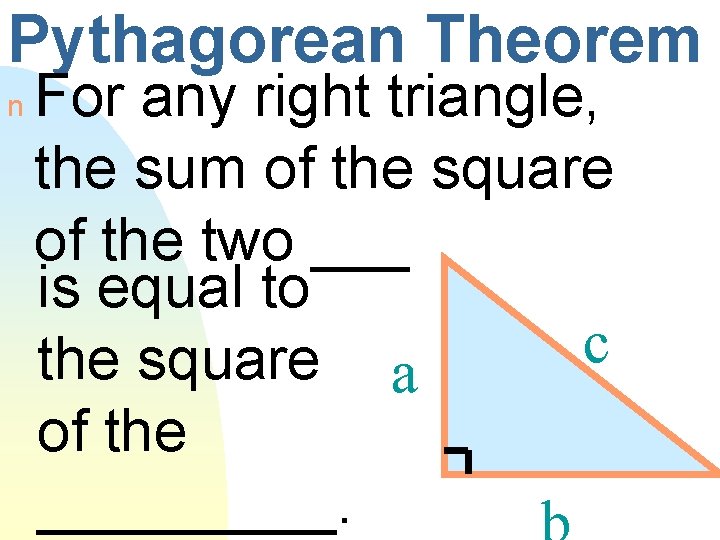
Pythagorean Theorem n For any right triangle, the sum of the square of the two ___ is equal to c the square a of the _____.

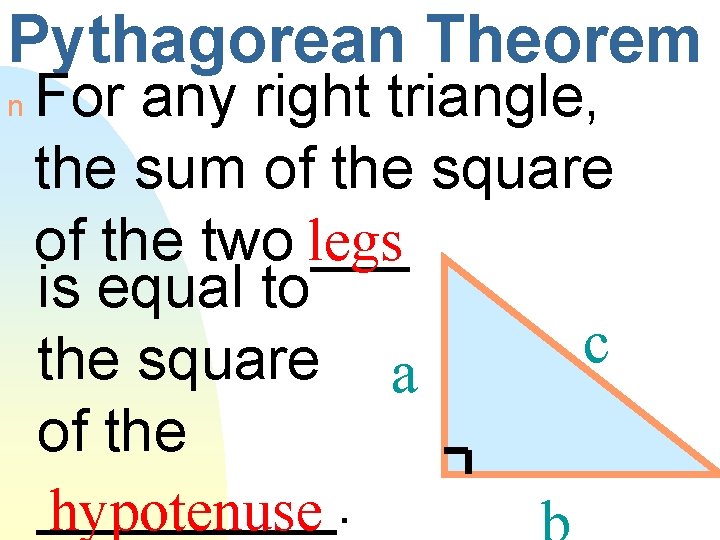
Pythagorean Theorem n For any right triangle, the sum of the square of the two legs ___ is equal to c the square a of the _____. hypotenuse

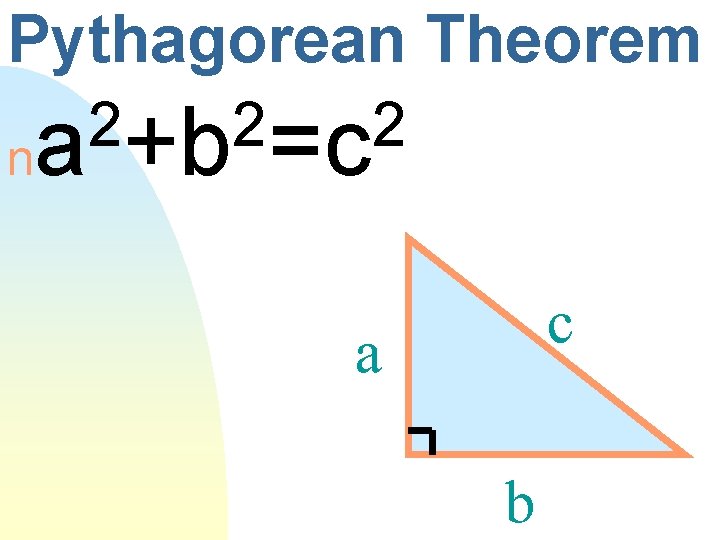
Pythagorean Theorem 2 2 2 na +b =c c a b

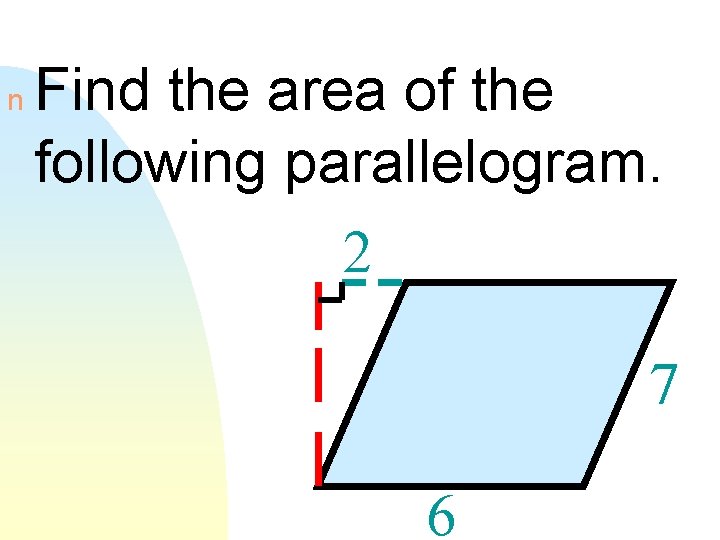
n Find the area of the following parallelogram. 2 7 6

How do I determine if a triangle is acute, obtuse or right, given its side lengths?

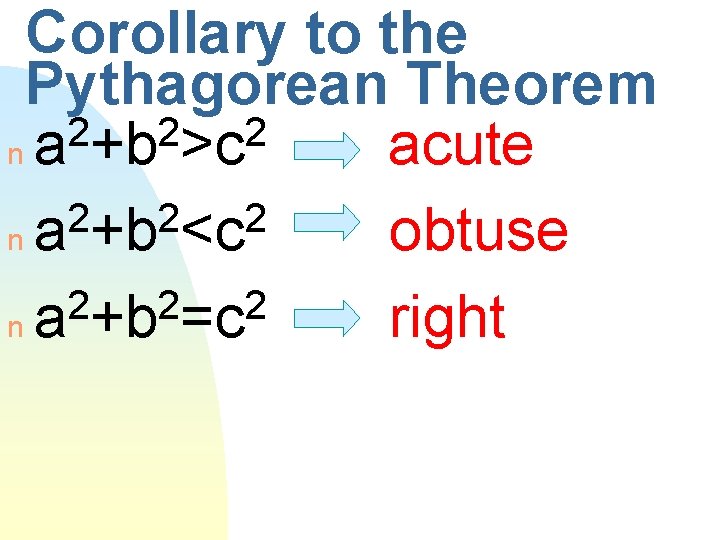
Corollary to the Pythagorean Theorem n If the sum of the squares of the two shorter sides of a triangle is less than the square of the longest side, then the triangle is

Corollary to the Pythagorean Theorem n If the sum of the squares of the two shorter sides of a triangle is less than the square of the longest obtusethen the triangle is side,

Corollary to the Pythagorean Theorem n If the sum of the squares of the two shorter sides of a triangle is greater than the square of the longest side, then the triangle is

Corollary to the Pythagorean Theorem n If the sum of the squares of the two shorter sides of a triangle is greater than the square of the longest acute side, then the triangle is

Corollary to the Pythagorean Theorem n If the sum of the squares of the two shorter sides of a triangle is equal to the square of the longest side, then the triangle is

Corollary to the Pythagorean Theorem n If the sum of the squares of the two shorter sides of a triangle is equal to the square of the longest right then the triangle is side,

Corollary to the Pythagorean Theorem 2 2 2 n a +b >c acute 2 2 2 n a +b <c obtuse 2 2 2 n a +b =c right

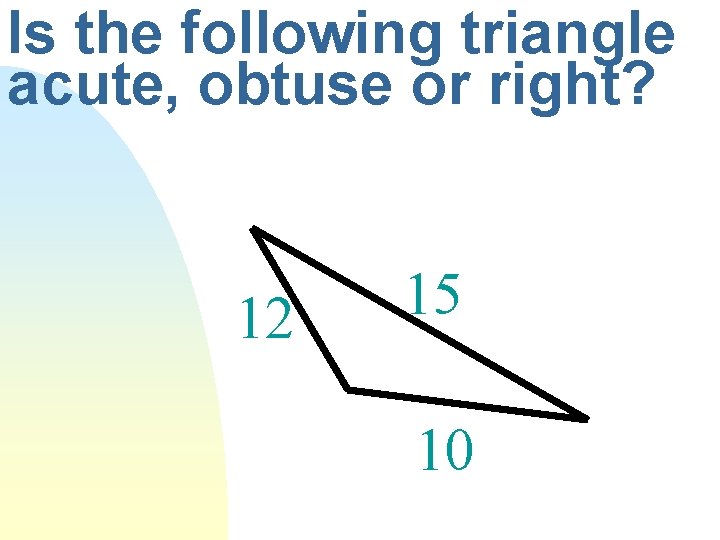
Is the following triangle acute, obtuse or right? 12 15 10

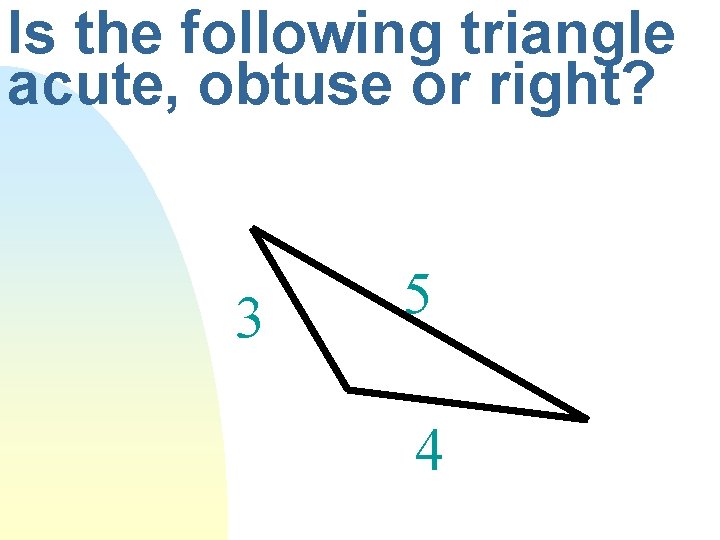
Is the following triangle acute, obtuse or right? 3 5 4

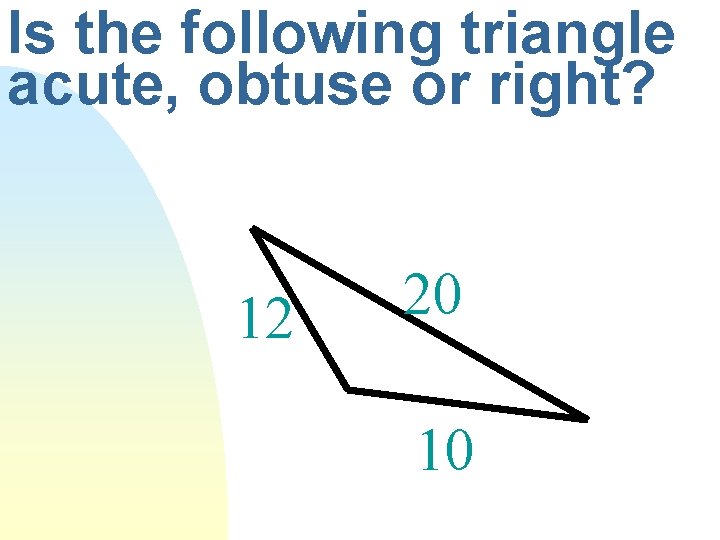
Is the following triangle acute, obtuse or right? 12 20 10

Try These n P 259 #’s 1 -10; 11 -21 odd, 25 -29 odd; 33 -36 all