Myriorama cards were invented in France around 1823

Myriorama cards were invented in France around 1823 by Jean -Pierre Brès and further developed in England by John Clark. Early myrioramas were decorated with people, buildings, and scenery that could be laid out in any order to create a variety of landscapes. One 24 -card set is sold as “The Endless Landscape. ” How many different landscapes could be created? Math 30 -1 1

11. 3 The Binomial Theorem Student Activity Race Expand (x + y)0 (x + y)3 (x + y)1 (x + y)2 (x + y)4 (x + y)5 Math 30 -1 2

Pascal’s Triangle and the Binomial Theorem (x + y)n, n ∈ N (x + y)0 = 1 (x + y)1 = 1 x + 1 y (x + y)2 = 1 x 2 + 2 xy + 1 y 2 (x + y)3 = 1 x 3 + 3 x 2 y + 3 xy 2 +1 y 3 (x + y)4 = 1 x 4 + 4 x 3 y + 6 x 2 y 2 + 4 xy 3 + 1 y 4 (x + y)5 = 1 x 5 + 5 x 4 y + 10 x 3 y 2 + 10 x 2 y 3 + 5 xy 4 + 1 y 5 (x + y)6 = 1 x 6 + 6 x 5 y 1 + 15 x 4 y 2 + 20 x 3 y 3 + 15 x 2 y 4 + 6 xy 5 + 1 y 6 What is the relationship between the value of n and the number of terms in the expansion? Math 30 -1 3

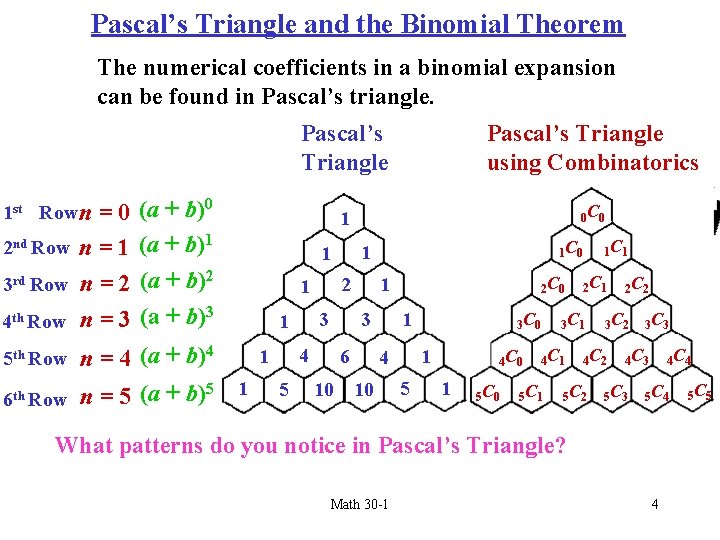
Pascal’s Triangle and the Binomial Theorem The numerical coefficients in a binomial expansion can be found in Pascal’s triangle. 1 st Row n =0 2 nd Row n = 1 3 rd Row n = 2 4 th Row n = 3 (a + b)0 (a + b)1 (a + b)2 (a + b)3 n = 4 (a + b)4 5 6 th Row n = 5 (a + b) Pascal’s Triangle using Combinatorics 1 0 C 0 2 1 3 1 1 5 6 10 2 C 0 1 3 4 1 5 th Row 1 C 1 1 C 0 1 1 4 10 3 C 0 5 4 C 0 1 5 C 0 2 C 1 3 C 1 4 C 1 5 C 1 3 C 2 4 C 2 5 C 2 2 C 2 3 C 3 4 C 3 5 C 3 4 C 4 5 C 4 What patterns do you notice in Pascal’s Triangle? Math 30 -1 4 5 C 5

The Binomial Theorem is a formula used for expanding powers of binomials. (a + b)3 = (a + b)(a + b) = a 3 + 3 a 2 b + 3 ab 2 + b 3 • The first term has no b. It is like choosing no b from three b’s. The combination 3 C 0 is the coefficient of the first term. • The second term has one b. It is like choosing one b from three b’s. • The combination 3 C 1 is the coefficient of the second term. • The third term has two b’s. It is like choosing two b’s from three b’s. The combination 3 C 2 is the coefficient of the third term. • The fourth term has three b’s. It is like choosing three b’s from three b’s. The combination 3 C 3 is the coefficient of the fourth term. 2 b 1 + C ab 2 + C b 3 (a + b)3 = 3 C 0 a 3 b 0 + 3 CMath 1 a 30 -1 3 2 3 3 5

Binomial Expansion - the General Term (a + b)3 = a 3 + 3 a 2 b + 3 ab 2 + b 3 The degree of each term is 3. For the variable a, the degree descends from 3 to 0. For the variable b, the degree ascends from 0 to 3. (a + b)3 = 3 C 0 a 3 - 0 b 0 + 3 C 1 a 3 - 1 b 1 + 3 C 2 a 3 - 2 b 2 + 3 C 3 a 3 - 3 b 3 (a + b)n = n. C 0 an - 0 b 0 + n. C 1 an - 1 b 1 + n. C 2 an - 2 b 2 + …. . + n. Ck an - kbk The general term is the (k + 1)th term: tk + 1 = n. Ck xn - k yk The number of terms in the expansion of (a + b)n is n+1 Math 30 -1 6

How many terms are in the expansion of each binomial? If there are 17 terms in the expansion of the given binomial, what is the value of k? Math 30 -1 7

Binomial Expansion - Practice n=4 x = 3 x y=2 Expand the following. a) (3 x + 2)4 = 4 C 0 (3 x)4 (2)0 + 4 C 1 (3 x)3 (2)1 + 4 C 2 (3 x)2 (2)2+ 4 C 3 (3 x)1(2)3 + 4 C 4 (3 x)0(2)4 = 1(81 x 4) + 4 (27 x 3)(2) + 6 (9 x 2)(4) + 4(3 x)(8) + 1(16) = 81 x 4 + 216 x 3 + 216 x 2 + 96 x + 16 b) (2 x - 3 y)3 n=4 x = 2 x y = -3 y = 3 C 0(2 x)3(-3 y)0 + 3 C 1(2 x)2(-3 y)1 + 3 C 2(2 x)1(-3 y)2 + 3 C 3(2 x)0(-3 y)3 = 1(8 x 3)(1) + 3(4 x 2)(-3 y) + 3(2 x)(9 y 2) + 1(1)(-27 y 3) = 8 x 3 - 36 x 2 y + 24 x 1 y 2 - 2 y 3 Math 30 -1 8

Binomial Expansion - Practice c) (2 x - 3 x -1)5 = 5 C 0(2 x)5(-3 x -1)0 + 5 C 1(2 x)4(-3 x -1)1 + 5 C 2(2 x)3(-3 x -1)2 n=5 x = 2 x y = -3 x -1 + 5 C 3(2 x)2(-3 x -1)3 + 5 C 4(2 x)1(-3 x -1)4 + 5 C 5(2 x)0(-3 x -1)5 = 1(32 x 5) + 5(16 x 4)(-3 x -1) + 10(8 x 3)(9 x -2) + 10(4 x 2)(-27 x -3) + 5(2 x)(81 x -4) + 1(-243 x -5) = 32 x 5 - 240 x 3 + 720 x 1 - 1080 x -1 + 810 x -3 - 243 x -5 Math 30 -1 9

Finding a Particular Term in a Binomial Expansion a) Determine an expression for the eighth term in the expansion of (3 x - 2)11. t 8 = t 7 + 1 so k = 7 tk + 1 = n. Ck xn - k yk n = 11 x = 3 x y = -2 k=7 t 7 + 1 = 11 C 7 (3 x)11 - 7 (-2)7 t 8 = 11 C 7 (3 x)4 (-2)7 = 330(81 x 4)(-128) = -3 421 440 x 4 b) Determine the coefficient of the term containing Ax 2 y 5 in the expansion of(x - 3 y)7. tk + 1 = n. Ck xn - k yk n=7 k=5 Ax 2 y 5 = 7 C 5 (x)2(-3 y)5 = 21 (x 2)(-243 y 5) = -5103 x 2 y 5 Math 30 -1 10

Determine an expression for the term containing x 3 in the expansion of (2 x - 3)6. tk + 1 = n. Ck xn - k yk When the exponent on x is 3, and the value of n is 6, the value of k must be 3. t 3 + 1 = 6 C 3 (2 x)6 - 3 (-3)3 Math 30 -1 11

Determine the value of the constant term of the expansion of n = 18 x = 2 x y = -x -2 k=? tk + 1 = n. Ck xn - k yk tk + 1 = 18 Ck (2 x)18 - k (-x -2)k tk + 1 = 18 Ck 218 - k x 18 - k (-1)k x -2 k tk + 1 = 18 Ck 218 - k (-1)k x 18 - 3 k = x 0 18 - 3 k = 0 -3 k = -18 k=6 Substitute k = 6: t 6 + 1 = 18 C 6 218 - 6 (-1)6 x 18 - 3(6) t 7 = 18 C 6 212 (-1)6 Therefore, the constant term is 76 038 144. t 7 = 76 038 144 Math 30 -1 12

Determine a Particular Term in the Binomial One term in the expansion of (2 x - m)7 is -15 120 x 4 y 3. Determine an expression to represent m. tk + 1 = n. Ck an - k bk n=7 a = 2 x b = -m k=3 tk + 1 = 7 C 3 (2 x)4 (-m)3 tk + 1 = (35) (16 x 4) (-m)3 -15 120 x 4 y 3 = (560 x 4) (-m)3 Therefore, m is 3 y. 3 y = m Math 30 -1 13

Math 30 -1 14

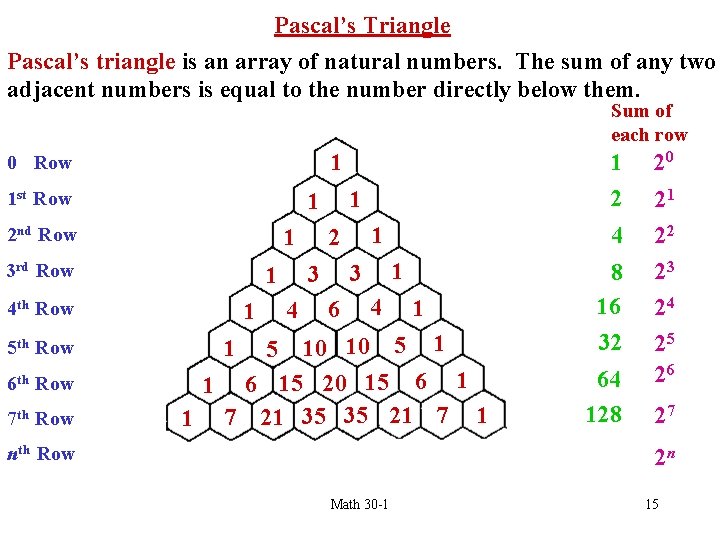
Pascal’s Triangle Pascal’s triangle is an array of natural numbers. The sum of any two adjacent numbers is equal to the number directly below them. Sum of each row 1 0 Row 1 st Row 1 3 rd Row 6 th Row 7 th Row 4 1 1 3 6 4 1 2 3 1 4 th Row 5 th Row 1 1 2 nd Row 1 2 4 1 10 10 5 1 1 6 15 20 15 6 1 1 7 21 35 35 21 7 1 1 5 nth Row 8 16 32 64 128 20 21 22 23 24 25 26 27 2 n Math 30 -1 15