Mx n n A programming language for scientific

Mx? n n A programming language for scientific computation. Related Languages: Matlab IDL Maple, Mathcad, Mathematica

Goals n n n Portability - interpreted and executed by a java interpreter. Efficiency - greatly improves programming efficiency. Program involving many matrix and vector operations are very short in Mx. Ease of use - very simple and quick to start

What can the language do? n n n Basic matrix operations – addition, multiplication… Advanced operations – matrix slicing and masking. Internal functions – Print, input, load, save, plot, paint

Operations and Relations Arithmetic Operations *, /, %, /’, ‘, +, - Logical Operations not and or Relational Operations >, >=, <, <=, ==, !=

Array and Range Specifier Array Constructor : i. e. . A[1: 10, 1: 2] : : i. e. . A[1: : 2] [1, 2; 3, 4]

Statements Block Statement {} iteration for (n = 1: 100); loop = if (exp) <stat>; if (exp) <stat> else <stat> break; continue; Assignments Conditional Statements Break and Continue

Functions and Function call Self Defined Functions func <id> (para-list) = exp; func <id> (paralist){} Function Call id(para-list); Note: can either be stand-lone or right value depends on if it has returned value

Internal functions • Console output print() print arguments to the standard output one by one. • Picture drawing paint() draws a matrix in a new window as an image plot() takes a matrix and plots it as a graph • Color color() sets the current color (in RGB) colormap() take a matrix with rows as RGB, and sets a colormap. • File I/O functions load( file, type, m, n ) save( matrix, file, type ) • Matrix generator zeros( m, n ) random( m, n ) • matrix operator inv( matrix ) flip( matrix )

Example 1: Mr. Potato A = load( "potato. dat", "byte", 128 ); colormap(1); paint( [ A, flip(A), mirror(A), flip(mirror(A)); A', flip(A'), mirror(A'), flip(mirror(A'))] ); return 0;

Overview of the interpreter n. Currently the Mx programming language is implemented interpretively. n. The interpreter parses and executes the user input or programs in files, and generates printed output and/or pictures. n. The parser of the interpreter is written in Antlr, and the rest routines are in Java. n. For a small portion of our code, we tried macro expansion in Java. n. Adequate functionalities made our project quite large, luckily most of the functions are tested and work well (maybe we have forgotten the existences of some functions? )

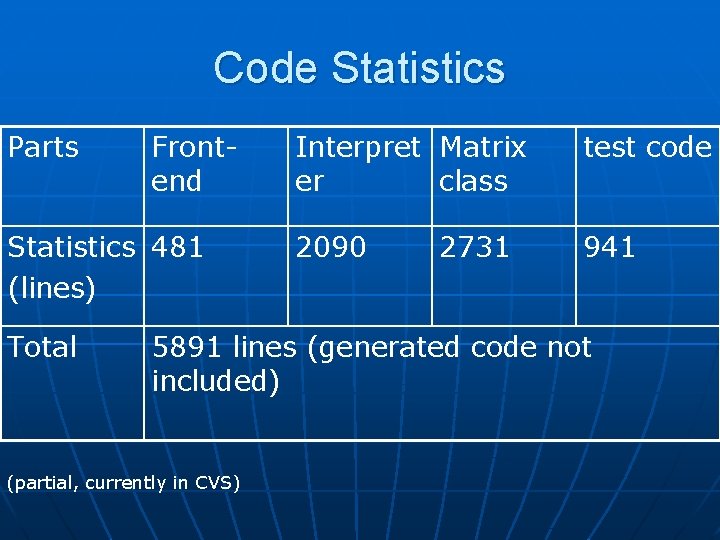
Code Statistics Parts Frontend Statistics 481 (lines) Total Interpret Matrix er class test code 2090 941 2731 5891 lines (generated code not included) (partial, currently in CVS)

Why another matrix class? • The Mx programming language has important functionalities: in-place matrix slicing and masking • Existing Java matrix classes do not support these

What can we do in Mx with slicing and masking? n A = zeros(256, 256); n A[10: 40, : ] = 1; n A[25: : 50, 60: : 50] = random(50, 50); n A[A>=0. 75 or A<=0. 25] = 0. 5; n A[100: 199, 100: 199] = random(100, 100) + A[0: : 100, 0: : 100]*A[0: : 100, 100: : 100] ;

An example of masking: paint selected entries n n n n A = load( "mri-anat. sdt", "short", 256 ); B = load( "mri-func. fdt", "float", 256 ); A = flip(A'); B = flip(B'); paint( A ); colormap(4); opaint( B, B>0. 7, 0, 0, 0. 7, 1. 0 );

The features of our matrix class n n n n Arithmetic operations: + - * /. . . Sharing data between matrices Matrix slicing and masking Inversion and solving linear equations Comparing matrices Painting and plotting Transpose, flipping and mirroring And more. . .

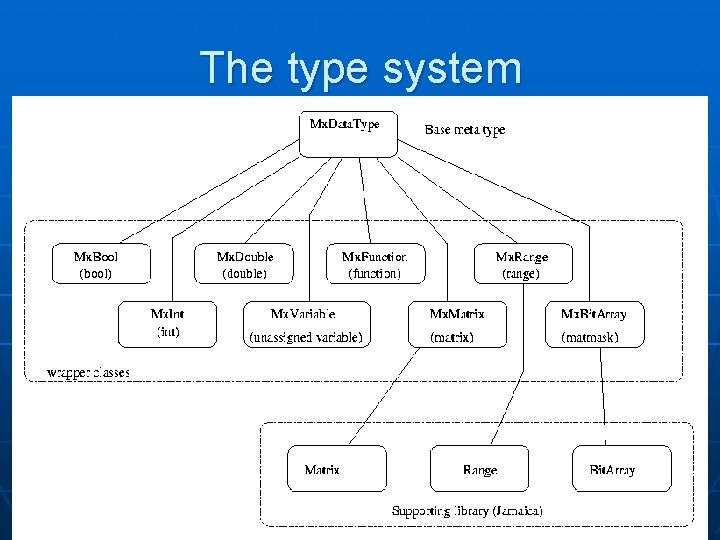
The type system

Testing Plan • 3 Stages: • Unit Testing n Creation of our own library using Matlab as guidance. n Library contains its own unit testing program. • Regressive Testing n Creation of a script to automate regressive testing written in tcl n Takes a database of one or more *. mx programs n See example

Example of the Testing Database ; ; ; samples. tdb: a sample of testing ; ; ; database for the Mx ; ; assign 1 2 3 4 { a = [1, 2; 3. 4]; return a; } ; ; transpose 1 3 2 4 { a = [1. 2; 3, 4]’ ; return a; } ; ; transpose 1 2 3 4 { a = [1, 2; 3, 4]’’ ; return a; } ; ; triple transposes 1 2 4 { return [1; 2; 4]’’’ ; } ; ; matrix add 1 2 3 4 { return [1, 1; 1, 1] + [0, 1; 2, 3]; }

Testing Plan • Advanced Testing n Necessity for larger testing programs n Integrated all the examples from the tutorial and used them as our advanced testing examples.

Lessons Learned 1. Fully investigate the feasibility of the supporting tools n Original Matrix classes lacked many functions n Plotting, painting, masking, etc. 2. Get advice from experienced 3. When an easier method of implementing classes of function exists, use it