MustKnow ROOT Class IOTGraphTntupleTtree 1 IO Saving Objects

Must-Know ROOT Class I/O/TGraph/Tntuple/Ttree/…. 1

I/O : Saving Objects in ROOT • Use the TFile class –we need first to create the class, which opens the file TFile* f = TFile: : Open("file. root", "NEW"); • • Write an object deriving from TObject: object->Write("optional. Name") For any other object (but with dictionary) f->Write. Object(object, "name"); 2

TFile Class • ROOT stores objects in TFiles: – TFile* f = TFile: : Open("file. root", "NEW"); • TFile behaves like file system: – f->mkdir("dir"); • TFile has a current directory: – f->cd("dir"); • You can browse the content: – f->ls(); TFile**! ! file. root! TFile*! ! file. root! TDirectory. File*! dir KEY: TDirectory. File! dir; 1!dir • Tbrowser b; 3

TGraph. Errors() TGraph. Errors(Int_t n) TGraph. Errors(const TGraph. Errors& gr) TGraph. Errors(const TH 1* h) TGraph. Errors(const char* filename, const char* format = "%lg %lg %lg", Option_t* option = "") TGraph. Errors(Int_t n, const Double_t* x, const Double_t* y, const Double_t* ex = 0, const Double_t* ey = 0) 4

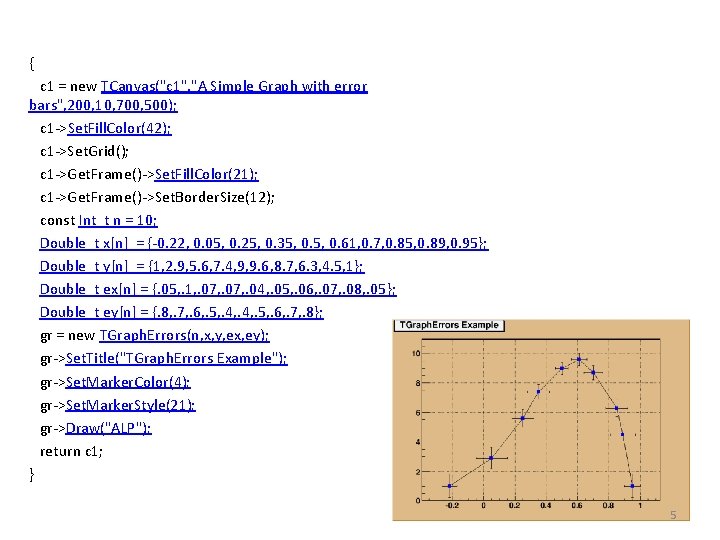
{ c 1 = new TCanvas("c 1", "A Simple Graph with error bars", 200, 10, 700, 500); c 1 ->Set. Fill. Color(42); c 1 ->Set. Grid(); c 1 ->Get. Frame()->Set. Fill. Color(21); c 1 ->Get. Frame()->Set. Border. Size(12); const Int_t n = 10; Double_t x[n] = {-0. 22, 0. 05, 0. 25, 0. 35, 0. 61, 0. 7, 0. 85, 0. 89, 0. 95}; Double_t y[n] = {1, 2. 9, 5. 6, 7. 4, 9, 9. 6, 8. 7, 6. 3, 4. 5, 1}; Double_t ex[n] = {. 05, . 1, . 07, . 04, . 05, . 06, . 07, . 08, . 05}; Double_t ey[n] = {. 8, . 7, . 6, . 5, . 4, . 5, . 6, . 7, . 8}; gr = new TGraph. Errors(n, x, y, ex, ey); gr->Set. Title("TGraph. Errors Example"); gr->Set. Marker. Color(4); gr->Set. Marker. Style(21); gr->Draw("ALP"); return c 1; } 5

Ntuple/TTree • Ntuple class – Tntuple • For storing tabular data • Eg. Excel talbe with numbers • Tree class – Ttree • For storing complex data types • E. g Database tables 6

Building ROOT Ntuple • Creating and Storing N-tuples –The ROOT class TNtuple can store only floating entries – each raw (record) must be composed only of floating types • Specify the name (label) of the type when creating the object TNtuple data(“ntuple”, ”Example N-tuple”, ”x: y: z: t”); // fill it with random data for (int i = 0; i<10000; ++i) { float x = g. Random->Uniform(-10, 10); float y = g. Random->Uniform(-10, 10); float z = g. Random->Gaus(0, 5); float t = g. Random->Exp(10); data. Fill(x, y, z, t); } // write in a file TFile f(“ntuple_data. root”, ”RECREATE”); data. Write(); f. Close(); 7

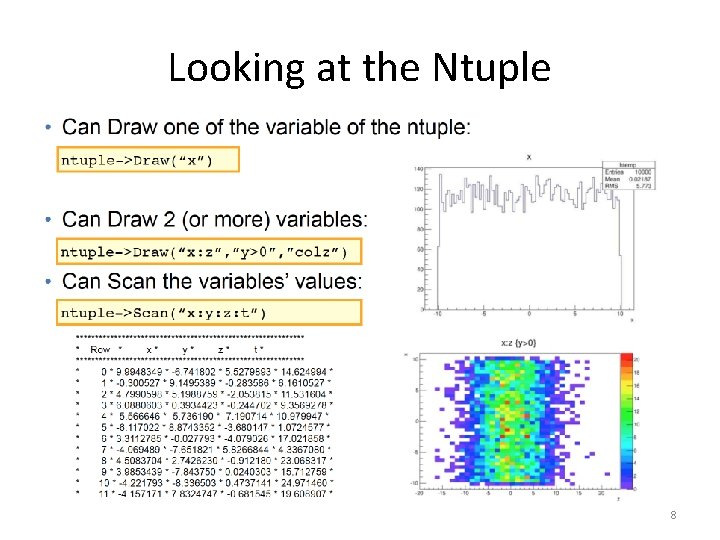
Looking at the Ntuple 8

Getting The Entries • Entries of a ROOT N-tuple can be retrieved using • TNtuple: : Get. Entry(irow) TFile f("ntuple_data. root"); TNtuple *ntuple=0; f. Get. Object("ntuple", ntuple); // loop on the ntuple entries for (int i = 0; i < ntuple->Get. Entries(); ++i) { ntuple->Get. Entry(i); float * raw_content = ntuple->Get. Args(); float x = raw_content[0]; float y = raw_content[1]; float z = raw_content[2]; float t = raw_content[3]; // do something with the data. . } 9

TTree • ROOT N-tuple can store only floating point variables • For storing complex types, i. e. objects we can use the ROOT tree class, TTree – TNtuple is a special case of a TTree (a derived class) • The ROOT Tree is – extremely efficient write once, read many. – Designed to store >109 (HEP events) with same data structure. – Trees allow fast direct and random access to any entry (sequential access is the best). – Optimized for network access (read-ahead). 10

Why Ttrees ? • object. Write() is convenient for simple objects like histograms, but inappropriate for saving collections of events containing complex objects • Reading a collection: – read all elements (all events) • With trees: – only one element in memory, – or even only a part of it (less I/O) • Trees buffered to disk (TFile); – I/O is integral part of TTree concept 11

Tree Access • Databases have row wise access – Can only access the full object (e. g. full event) • ROOT trees have column wise access – Direct access to any event, any branch or any leaf even in the case of variable length structures – Designed to access only a subset of the object attributes (e. g. only particles’ energy) – Makes same members consecutive, e. g. for object with position in X, Y, Z, and energy E, all X are consecutive, then come Y, then Z, then E. A lot higher zip efficiency! 12

Building a ROOT Tree • Steps to build a Tree – Create a TFile class – Tree can be huge �need file for swapping filled entries TFile*hfile=TFile: : Open("AFile. root", "RECREATE"); – Create a TTree class • Add a Branch (TBranch) to the TTree • Fill the tree with the data • Write the tree to file 13

Examples • http: //root. cern. ch/root/htmldoc/TTree. html • http: //root. cern. ch/drupal/content/howtos#trees 14

Next Lecture on. . • A Simple MC code ( can be covered in Exercise session ) • Pythia Event Generator – http: //home. thep. lu. se/~torbjorn/Pythia. html – PYTHIA is a program for the generation of high-energy physics events, i. e. for the description of collisions at high energies between elementary particles such as e+, e-, p and pbar in various combinations. It contains theory and models for a number of physics aspects, including hard and soft interactions, parton distributions, initial- and final-state parton showers, multiple interactions, fragmentation and decay. It is largely based on original research, but also borrows many formulae and other knowledge from the literature. 15