Musical Sounds Physical Science 101 Chapter twenty Amanda

Exercise What is decibel level of a sound that is 1000 times louder than

What Exercise is decibel level of a sound that is 10, 000 times

it’s actually easy intensity 10 (101) louder 10 d. B higher intensity 100 (102)

What Exercise is decibel level of a sound that is 1000 times louder

Quality The quality of sound from a musical instrument depends on the number of

Fourier Any periodic signal can be made up from a sum of harmonic waves

Fourier (1, 0, -(1/9)) Any periodic signal can be made up from a sum

Fourier (1, 0, -(1/9), 0, +(1/25)) Any periodic signal can be made up from

Fourier (1, 0, -(1/9), 0, 1/25, 0, -(1/49), 0)

Fourier (1, 0) Any periodic signal can be made up from a sum of

Fourier (1, 0, (1/3)) Any periodic signal can be made up from a sum

Fourier (1, 0, 1/3, 0, 1/5) Any periodic signal can be made up from

Fourier (1, 0, 1/3, 0, 1/5, 0, 1/7) Any periodic signal can be made

Compact Discs binary numbers 00 01 10 11 100 101 10000 1111 0 1

Compact Discs Sample rate of 44, 100 bytes per second This gives 0 to

Slides: 29

Download presentation

Musical Sounds Physical Science 101 Chapter twenty Amanda Hyer

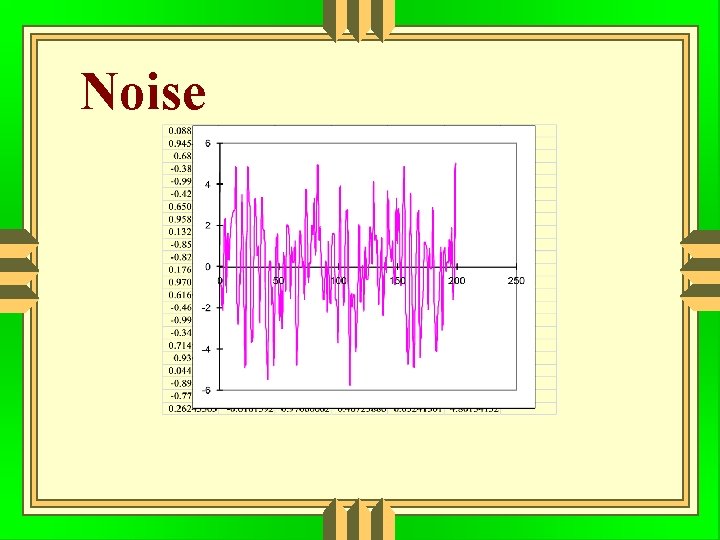
Noise

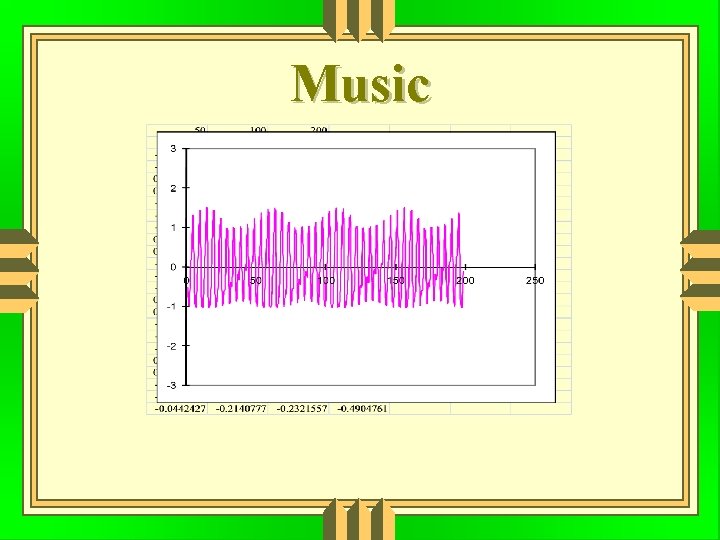
Music

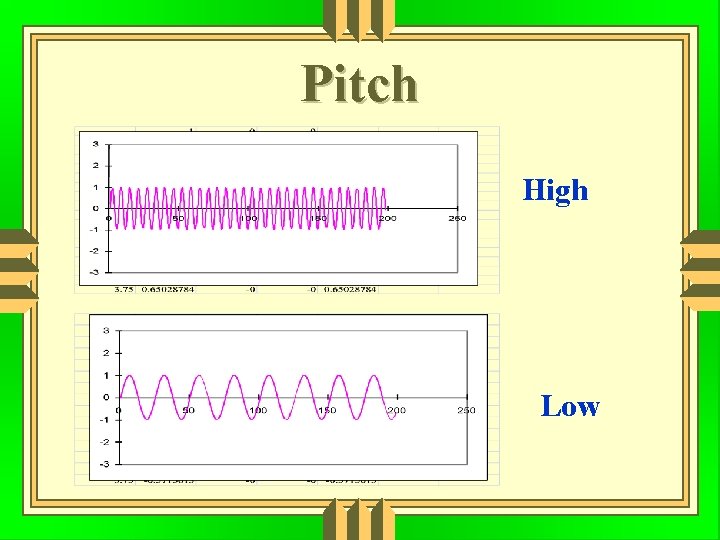
Pitch High Low

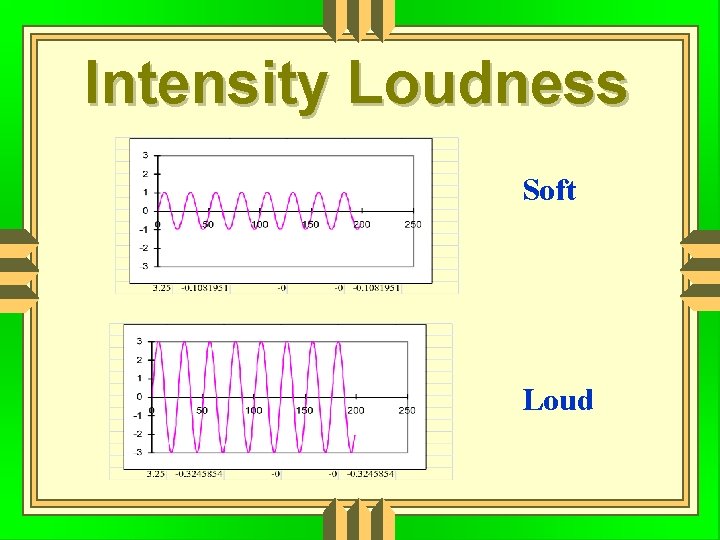
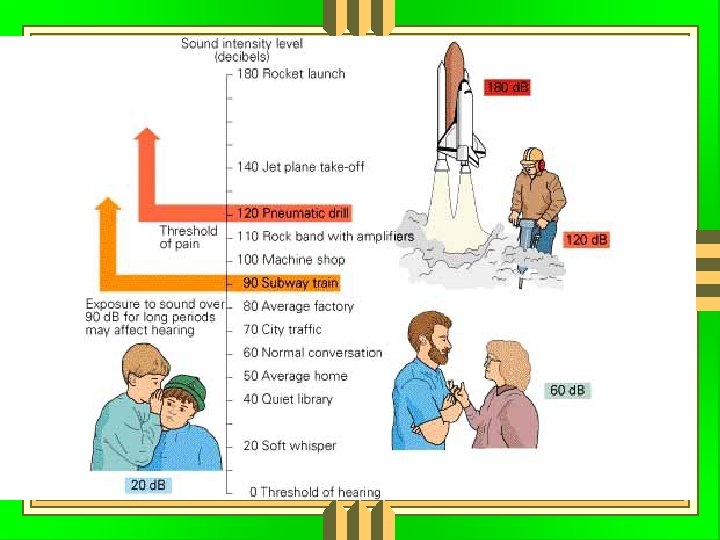
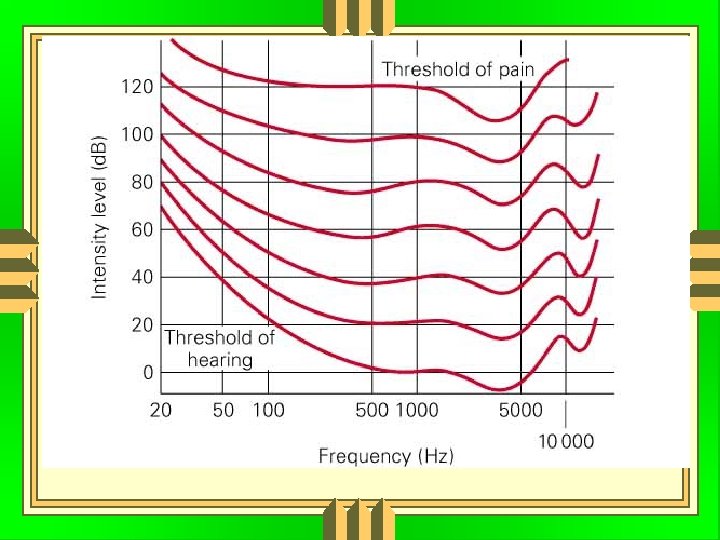
Intensity Loudness Soft Loud

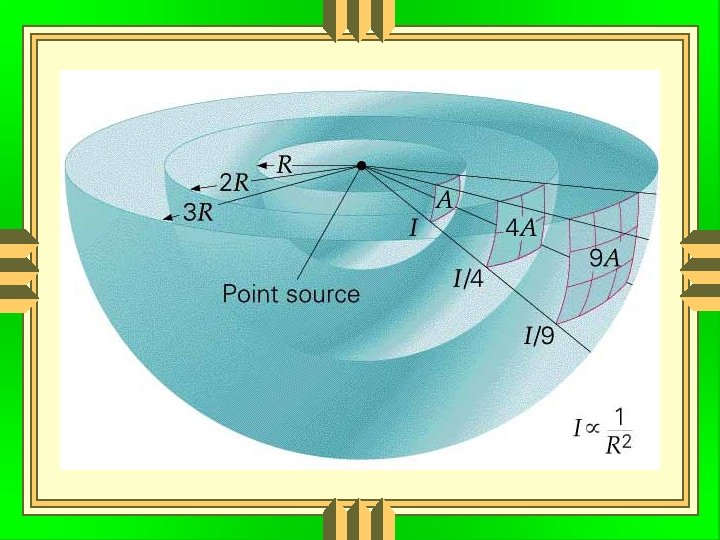
Sound Intensity

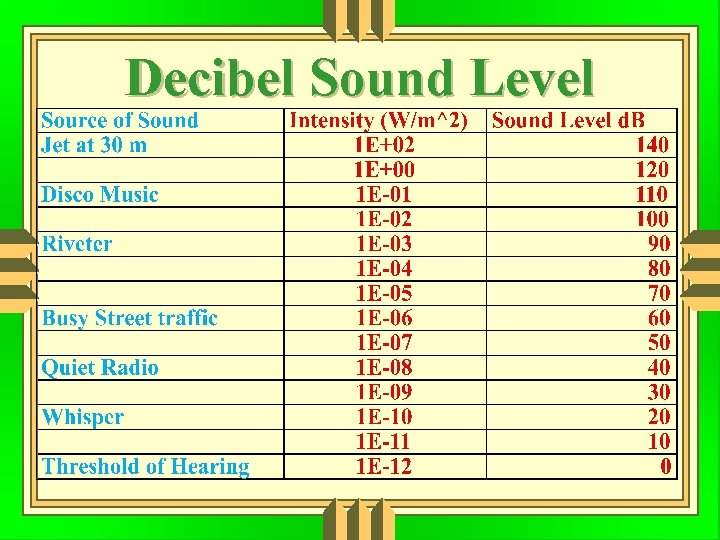
Decibel Sound Level

Exercise What is decibel level of a sound that is 1000 times louder than the threshold of human hearing? Given: Intensity/10 -12=1000=103 Wanted: decibel level Solution: d. B=10 log(Intensity/10 -12) d. B=10 log(103) = 30 d. B

What Exercise is decibel level of a sound that is 10, 000 times louder than a sound of 50 d. B? Given: 50 d. B=d. B 1 and Int 2 =10, 000 Int 1 Wanted: d. B 2 Solution: Int 1=100, 000 (10 -12) Int 2=10, 000*100, 000 (10 -12)= 109(10 -12) d. B 2=10 log(109) = 90 d. B

it’s actually easy intensity 10 (101) louder 10 d. B higher intensity 100 (102) louder 20 d. B higher intensity 1000 (103) louder 30 d. B higher intensity 10, 000 (104) louder 40 d. B higher intensity 1, 000 (106) louder 60 d. B higher

What Exercise is decibel level of a sound that is 1000 times louder than a sound of 70 d. B? Given: 70 d. B=d. B 1 and Int 2 =1000 Int 1 Wanted: d. B 2 Solution: d. B 2 is 30 d. B higher d. B 2=70+30 d. B=100 d. B

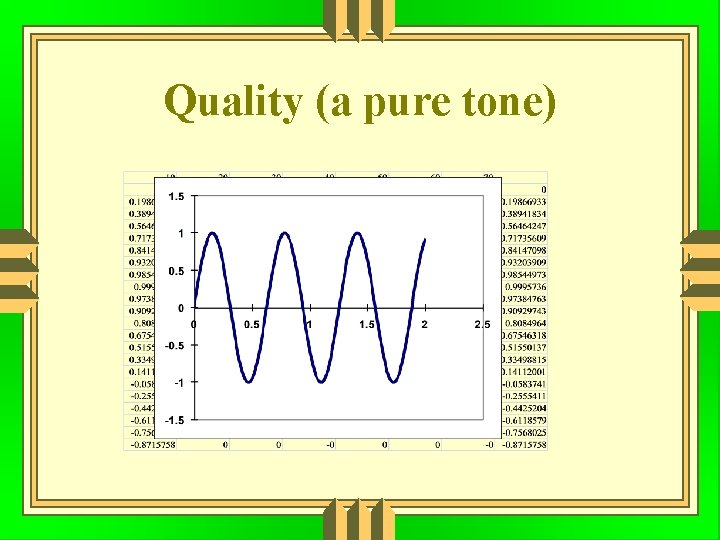
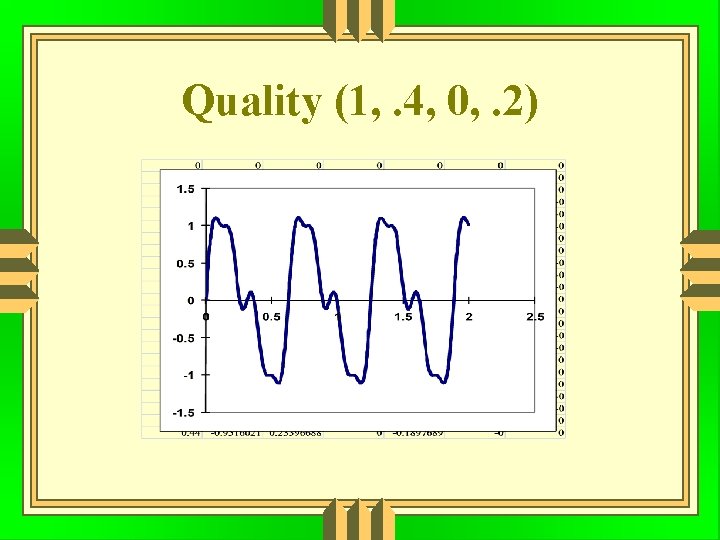
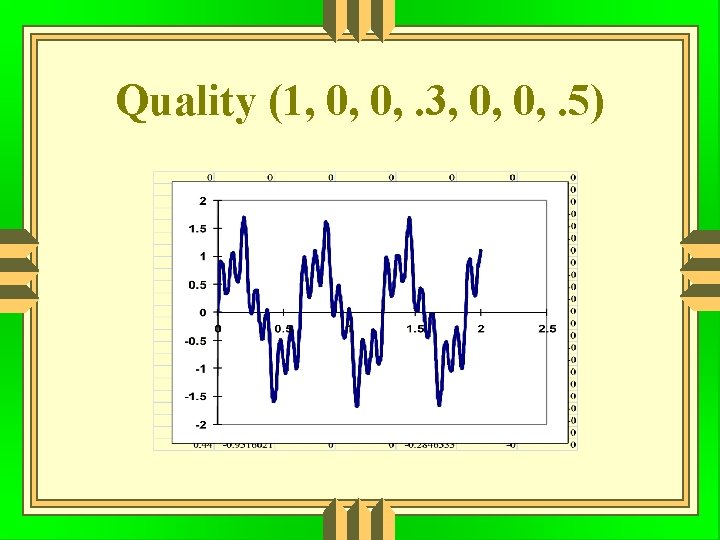
Quality The quality of sound from a musical instrument depends on the number of higher harmonics included with the fundamental frequency.

Quality (a pure tone)

Quality (1, . 4, 0, . 2)

Quality (1, 0, 0, . 3, 0, 0, . 5)

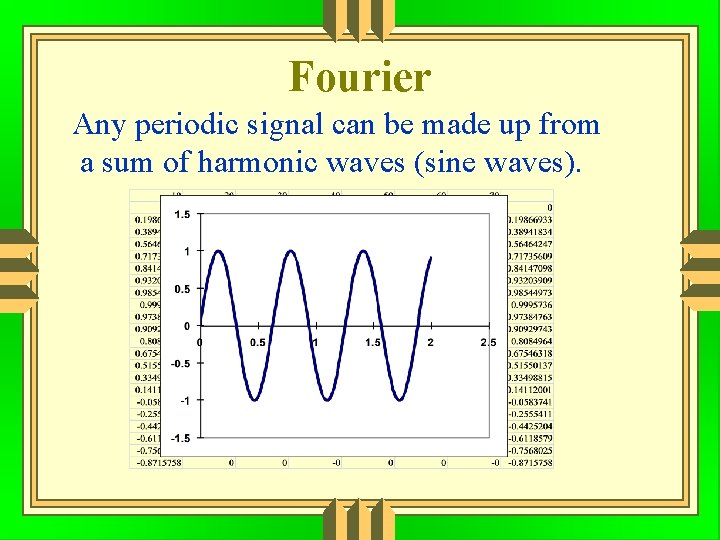
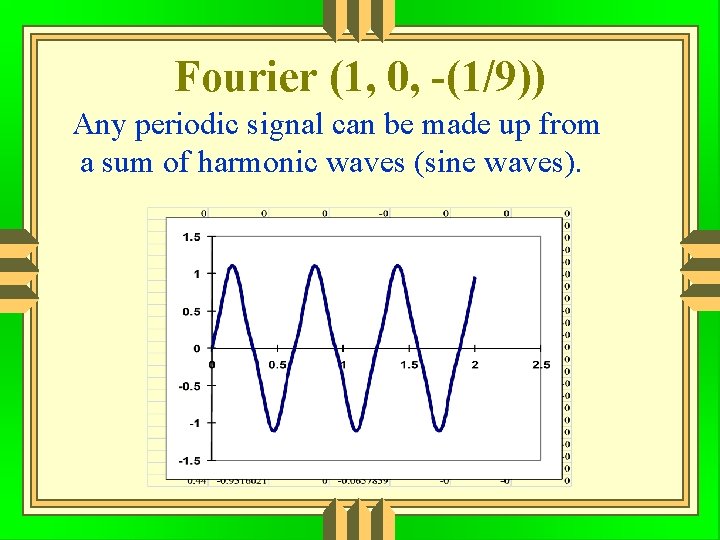
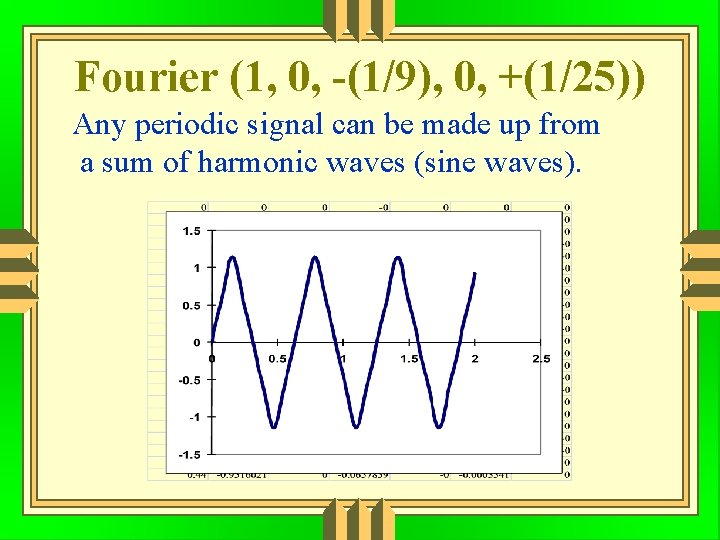
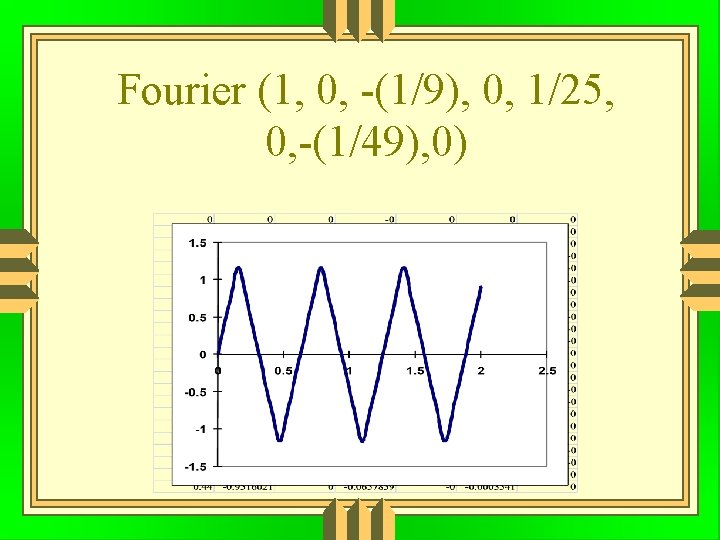
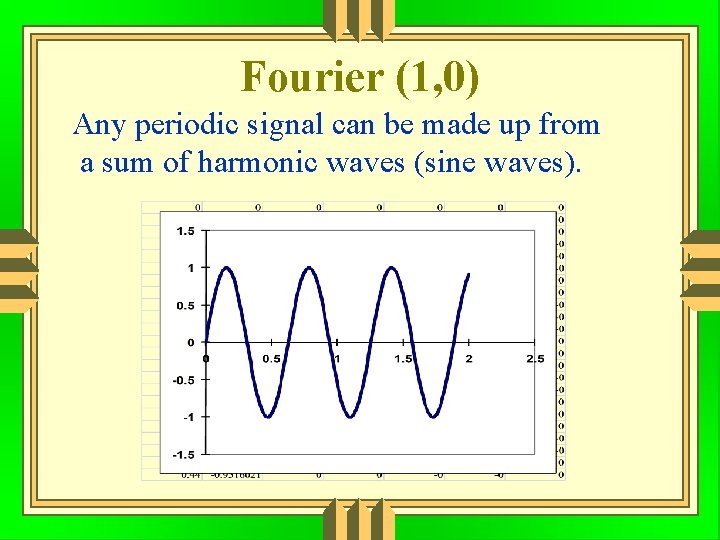
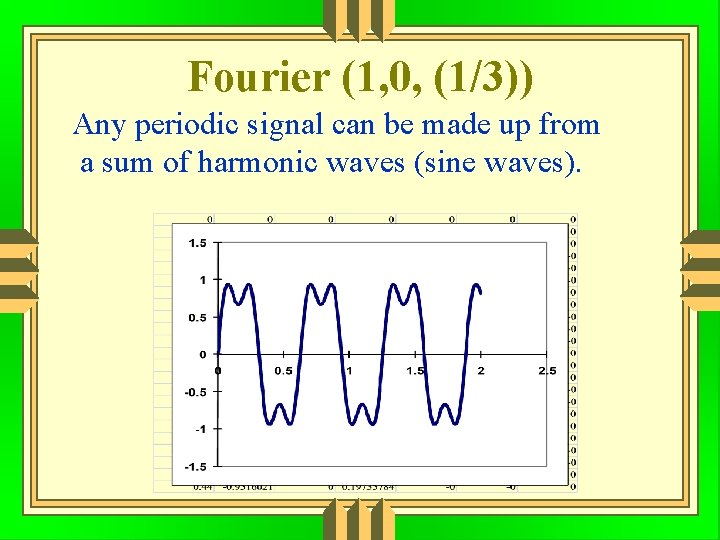
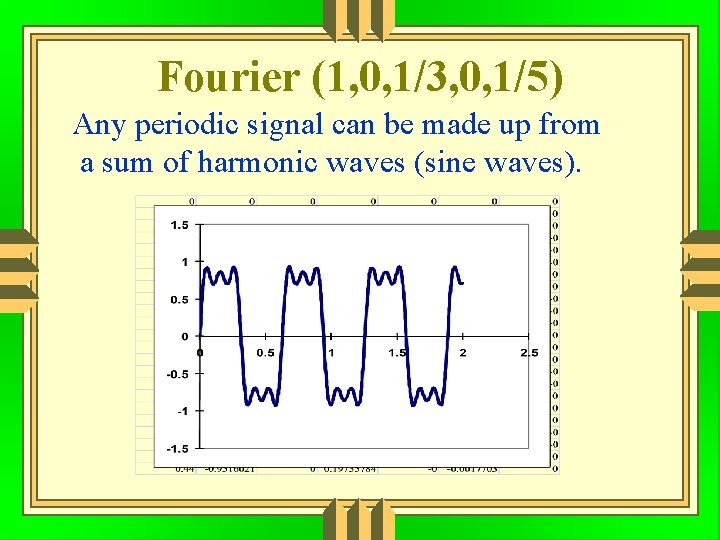
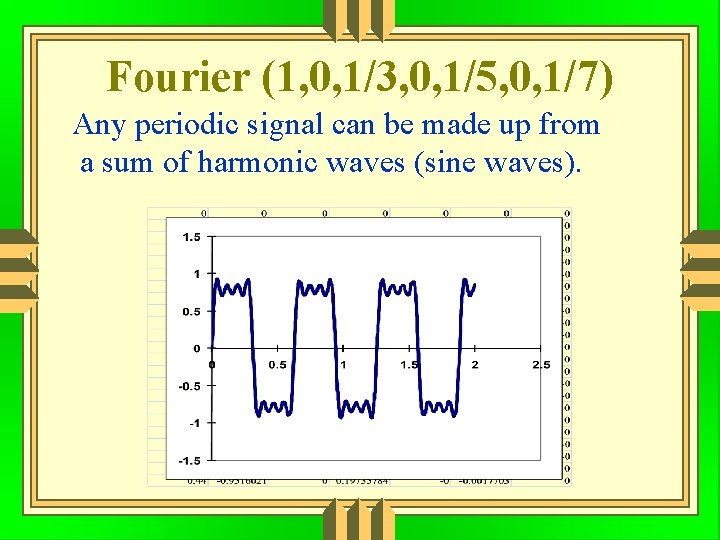
Fourier Any periodic signal can be made up from a sum of harmonic waves (sine waves).

Fourier (1, 0, -(1/9)) Any periodic signal can be made up from a sum of harmonic waves (sine waves).

Fourier (1, 0, -(1/9), 0, +(1/25)) Any periodic signal can be made up from a sum of harmonic waves (sine waves).

Fourier (1, 0, -(1/9), 0, 1/25, 0, -(1/49), 0)

Fourier (1, 0) Any periodic signal can be made up from a sum of harmonic waves (sine waves).

Fourier (1, 0, (1/3)) Any periodic signal can be made up from a sum of harmonic waves (sine waves).

Fourier (1, 0, 1/3, 0, 1/5) Any periodic signal can be made up from a sum of harmonic waves (sine waves).

Fourier (1, 0, 1/3, 0, 1/5, 0, 1/7) Any periodic signal can be made up from a sum of harmonic waves (sine waves).

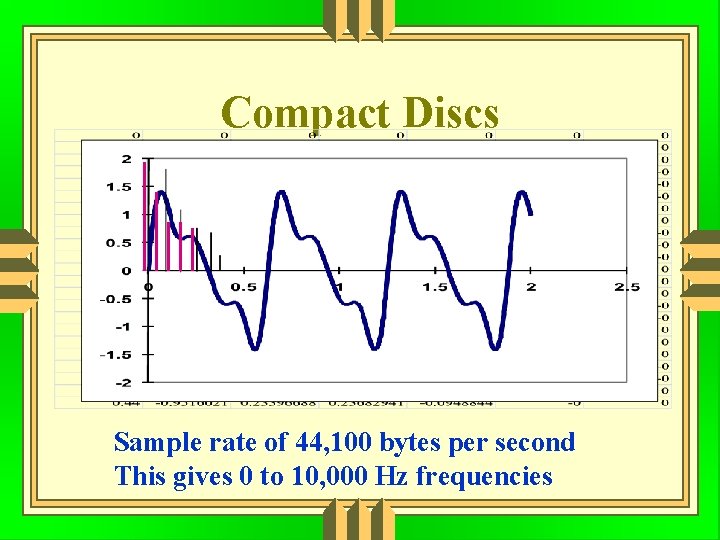
Compact Discs binary numbers 00 01 10 11 100 101 10000 1111 0 1 2 3 4=22 5 16=24 255

Compact Discs Sample rate of 44, 100 bytes per second This gives 0 to 10, 000 Hz frequencies