Muon Tomography for Detection of Nuclear Contraband with

Muon Tomography for Detection of Nuclear Contraband with High Performance Computing Infrastructure FAS - Mar. ‘ 08 J. Helsby, P. Ford, R. Hoch, K. Gnanvo, R. Pena, M. Hohlmann, D. Mitra Florida Tech Florida Academy of Sciences, Jacksonville University, Jacksonville, FL, Mar 14, 2008 3/14/2008 J. Helsby - Florida Academy of Sciences, Jacksonville University, FL

Introduction • Muon Tomography first used by Luis Alvarez to look for hidden chambers in the pyramids at Giza in the 1960 s. • Use GEANT 4/Cr. Y to simulate scenarios of shipping containers carrying nuclear contraband. • Use an algorithm to reconstruct the scattering angles and scatter positions associated with those angles. • Feasibility Study of possible detections (resolution required, ability to differentiate materials etc. ). 3/14/2008 J. Helsby - Florida Academy of Sciences, Jacksonville University, FL 2

Cosmic Ray Muons Mass =105. 7 Me. V Flux at Sea Level = 10, 000 muon/m 2/min Zenith angle distribution about 0º Average Energy at Sea Level = 4 Ge. V Why muons? Low radiation dose Noninvasive No source Penetrate through shielding 3/14/2008 J. Helsby - Florida Academy of Sciences, Jacksonville University, FL 3
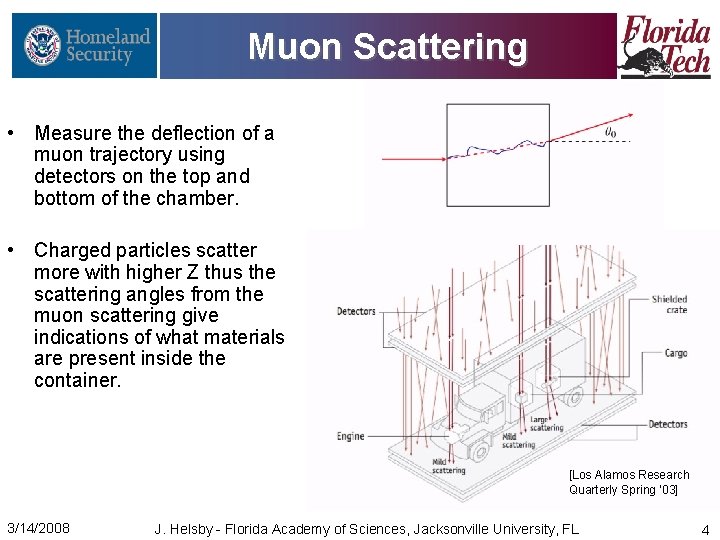
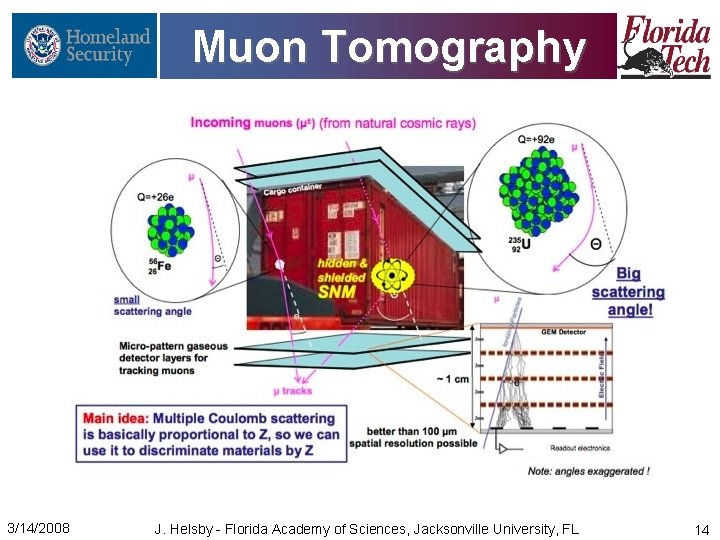
Muon Scattering • Measure the deflection of a muon trajectory using detectors on the top and bottom of the chamber. • Charged particles scatter more with higher Z thus the scattering angles from the muon scattering give indications of what materials are present inside the container. [Los Alamos Research Quarterly Spring ‘ 03] 3/14/2008 J. Helsby - Florida Academy of Sciences, Jacksonville University, FL 4
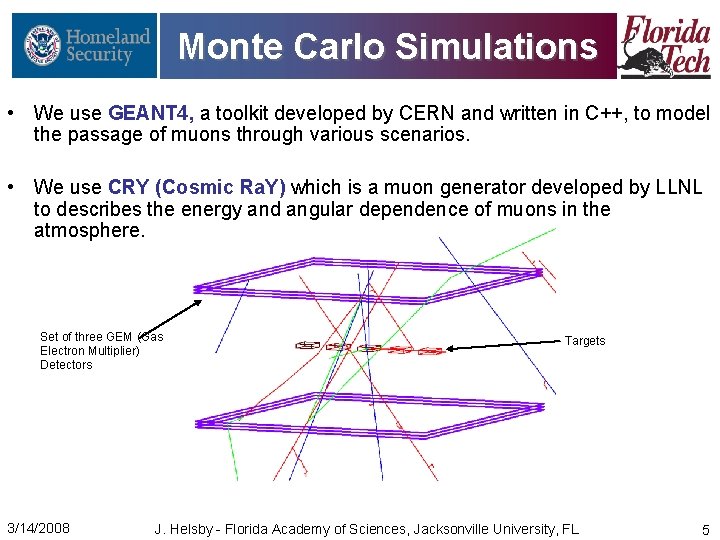
Monte Carlo Simulations • We use GEANT 4, a toolkit developed by CERN and written in C++, to model the passage of muons through various scenarios. • We use CRY (Cosmic Ra. Y) which is a muon generator developed by LLNL to describes the energy and angular dependence of muons in the atmosphere. Set of three GEM (Gas Electron Multiplier) Detectors 3/14/2008 Targets J. Helsby - Florida Academy of Sciences, Jacksonville University, FL 5

POCA • Point of Closest Approach (POCA) is the algorithm used to reconstruct the scatter points in the material. 3/14/2008 J. Helsby - Florida Academy of Sciences, Jacksonville University, FL 6
![Scenario: Low Z & High Z With GEM Detector Z [mm] “Perfect” Detector X Scenario: Low Z & High Z With GEM Detector Z [mm] “Perfect” Detector X](http://slidetodoc.com/presentation_image_h/efacfdd9a261829cf76a64a7ddf803e6/image-7.jpg)
Scenario: Low Z & High Z With GEM Detector Z [mm] “Perfect” Detector X [mm] Al Box: 20 cm x 20 cm U Box: 10 cm x 10 cm 2. 5 Million Events = 10 Min Exposure Time X [mm] 3/14/2008 J. Helsby - Florida Academy of Sciences, Jacksonville University, FL 7
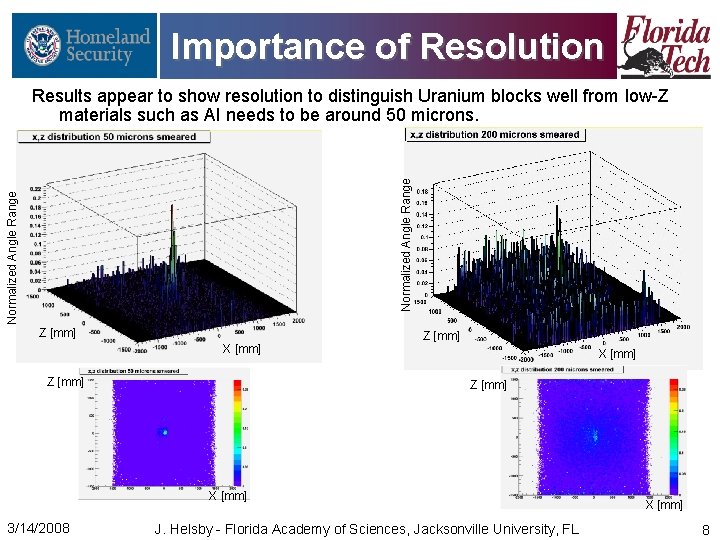
Importance of Resolution Normalized Angle Range Results appear to show resolution to distinguish Uranium blocks well from low-Z materials such as Al needs to be around 50 microns. Z [mm] X [mm] 3/14/2008 Z [mm] X [mm] J. Helsby - Florida Academy of Sciences, Jacksonville University, FL X [mm] 8
![Normalized Angle Range Scenario: High Z Z [mm] X [mm] As expected, when looking Normalized Angle Range Scenario: High Z Z [mm] X [mm] As expected, when looking](http://slidetodoc.com/presentation_image_h/efacfdd9a261829cf76a64a7ddf803e6/image-9.jpg)
Normalized Angle Range Scenario: High Z Z [mm] X [mm] As expected, when looking at similar Z materials next to one another, it is not apparent which is the Uranium. The dimensions of the boxes are visible in the 50 micron resolution only. 3/14/2008 J. Helsby - Florida Academy of Sciences, Jacksonville University, FL 9

Conclusion • Muon radiography is a highly promising method for detecting heavy materials in a low or medium Z background. • Detector resolution should be at or better than 50 microns in order to resolve 1 Liter objects well. • Future work: – Advanced analysis needs to be done to determine how well similar Z materials can be distinguished from one another. – Develop new reconstruction algorithm • Future challenge: – Developing large enough GEM detectors to achieve the 50 micron resolution. 3/14/2008 J. Helsby - Florida Academy of Sciences, Jacksonville University, FL 10

Extra Florida Academy of Sciences, Jacksonville University, Jacksonville, FL, Mar 14, 2008 3/14/2008 J. Helsby - Florida Academy of Sciences, Jacksonville University, FL

Mult. Coulomb Scattering 3/14/2008 J. Helsby - Florida Academy of Sciences, Jacksonville University, FL 12
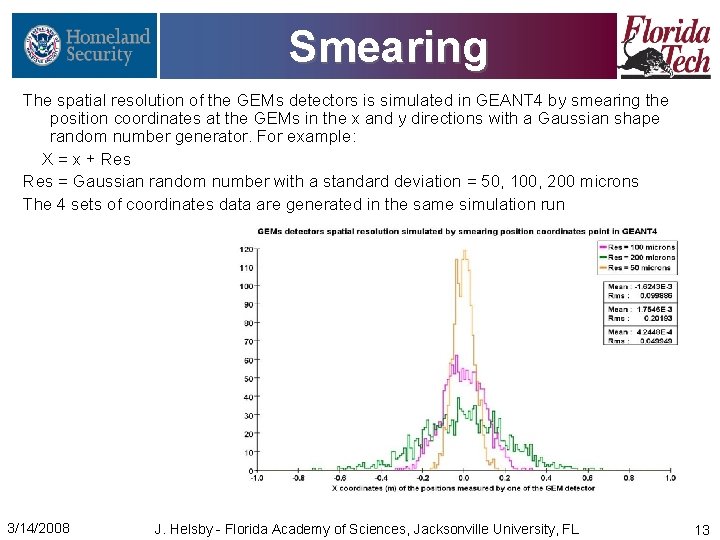
Smearing The spatial resolution of the GEMs detectors is simulated in GEANT 4 by smearing the position coordinates at the GEMs in the x and y directions with a Gaussian shape random number generator. For example: X = x + Res = Gaussian random number with a standard deviation = 50, 100, 200 microns The 4 sets of coordinates data are generated in the same simulation run 3/14/2008 J. Helsby - Florida Academy of Sciences, Jacksonville University, FL 13
Muon Tomography 3/14/2008 J. Helsby - Florida Academy of Sciences, Jacksonville University, FL 14
- Slides: 14