Multivariate Transformation Multivariate Transformations v Started in statistics

Multivariate Transformation

Multivariate Transformations v. Started in statistics of psychology and sociology. v. Also called multivariate analyses and multivariate statistics. v. Have been used by biological scientists since Fisher 1921. v. Different from all other forms of statistics. v. Explained in form of matrix algebra.

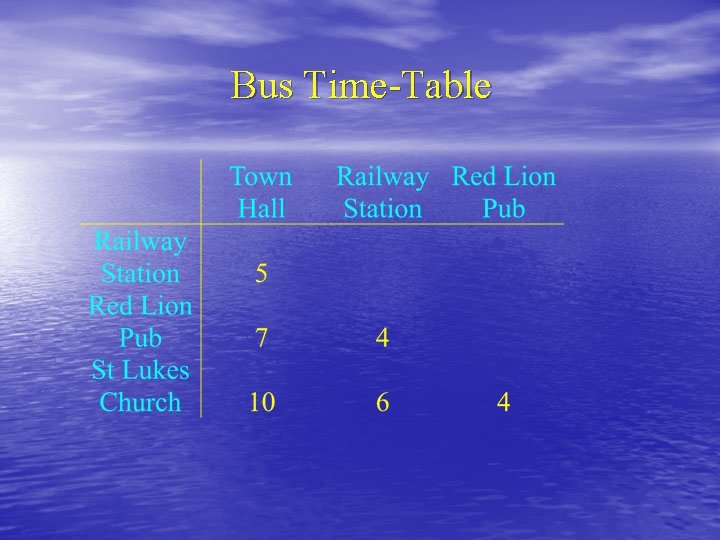
Bus Time-Table

Bus Time-Table

Bus Time-Table

Properties of Matrices Sum of leading diagonal is called the trace There is the possibility that a symmetrical matrix may be singular

Singular Matrices 4 7 -1 7 8 11 -1 11 -38 5 -3 -1 5 a -3 b -c = 0

Singular Matrices If A and B are symmetrical matrices, of size p x p then there are p values of A that make A - ΔB singular These values are called latentroots or eigen-values The multipliers (transformants) are called eigen-vectors

12 5 13 A= 5 13 4 21 1 B= 1 2 1 1 1 2 There should be 3 values of Δ that make A - ΔB singular One would be 21

12 5 13 A= 5 13 4 21 1 B= 1 2 1 1 1 2 There should be 3 values of Δ that make A - ΔB singular One would be 21 21 B= 21 21 21 -9 -16 -8 21 42 21 A- 21 B= -16 -29 -17 21 21 42 -8 -17 -21 Which has the eigen-vector [8 -5 1]

12 5 13 4 A= 13 4 21 1 B= 1 2 1 1 1 2 There should be 3 values of Δ that make A - ΔB singular Another one would be 6 6 B= 6 6 6 12 6 A- 6 B= -1 7 6 6 7 12 has the eigen-vector Which [1 -1 -1] -1 7 1 -2 -2 9

12 5 13 A= 5 13 4 21 1 B= 1 2 1 1 1 2 There should be 3 values of Δ that make A - ΔB singular Another one would be 7 7 B= 7 7 7 5 7 14 7 A- 6 B= -2 7 7 14 6 Which has the eigen-vector [4 1 -3] -2 6 -1 -3 -3 7

Eigen values and eigen vectors

Use of Singular Matrices v. Used in several multivariate transformations where A and B represent variability of sets of characters. v. Making A - ΔB singular may be regarded as subtracting B from A as often as possible, until the determinential value is zero.

What do plant scientists do? v. They test hypothesis: “Does this treatment affect the crop? ” v. They estimate a quantity in a hypothesis: “What is the expected yield increase resulting from adding 100 lbs of nitrogen? ” v. Multivariate transformations serve neither purpose, but rather they set hypothesis!

Why use multivariate Transformations Principal Components Canonical Analyses Reduce the dimensions of complex situations

Matrix of Interest XX’ = =A

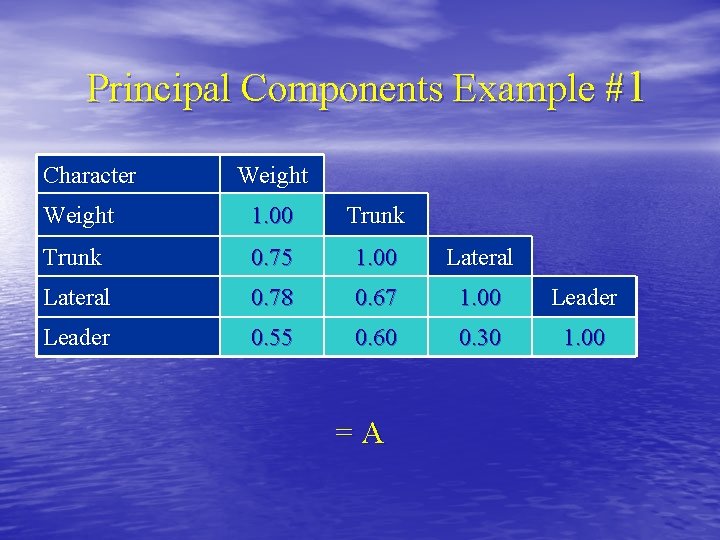
Principal Components Example #1 v. Extracted from the work of Moore. v. Concerned with the effect of size of apple trees at planting on future tree development v. Tree weight (w); trunk circumference squared (x); length of laterals (y) and length of central leader (z)

Principal Components Example #1 Character Weight 1. 00 Trunk 0. 75 1. 00 Lateral 0. 78 0. 67 1. 00 Leader 0. 55 0. 60 0. 30 1. 00 =A

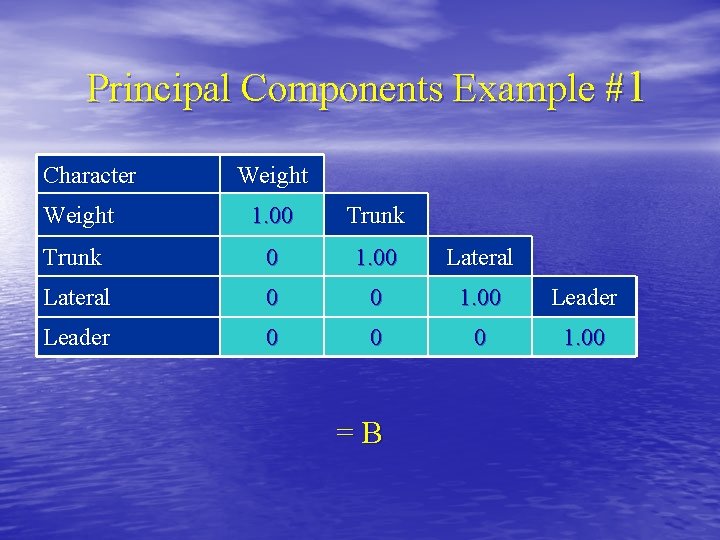
Principal Components Example #1 Character Weight 1. 00 Trunk 0 1. 00 Lateral 0 0 1. 00 Leader 0 0 0 1. 00 =B

Principal Components Example #1 v. The sum of the eigen values equals the trace of A (the original correlation matrix). v. The trace of A is the total variance of the four variables. v. The value of the eigen value indicates the proportion of the total variation that is accounted for by that transformation.

Principal Components Example #1

Principal Components Example #1

Principal Components Example #1

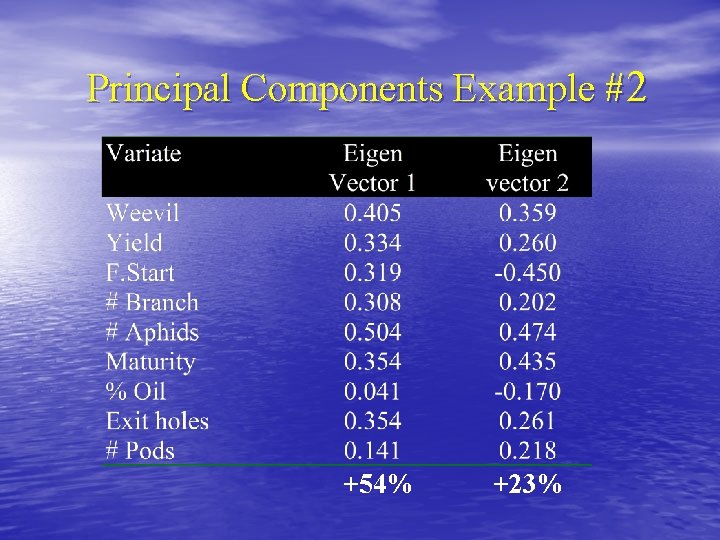
Principal Components Example #2 v. Twenty different Brassica cultivars. v. Effect of insect damage and plant morphology. v. Record 10 variables, three treatments.

Principal Components Example #2

Principal Components Example #2 +54% +23%

Principal Components Example #2

Principal Components Example #2 S. alba x B. napus

Problems for Statisticians ØIt should be noted that multivariate transformations are often speculative. ØAnalyses are laborious and require unique and specific computer software. ØThere are large dangers that we let the computer reduce the dimensions of a problem but in a non-biological manner.

Multivariate Transformations Applicable to multiple dimension problems Reduce the dimensions of complex problems Must be treated with knowledge of biological systems. Can be considered as a “try it and see” technique Can point researchers in the correct direction and indicates possible hypothesis that might be tested in future studies

Summary v. Association between characters. v. Simple linear regression model. v. Estimation of parameters. v. Analysis of variance of regression. v. Testing regression parameters (t tests).

Summary v. Prediction using regression. v. Outliers. v. Scatter diagrams. v. Making a curved line strait. v. Transformation, probit analysis. v. Optimal assent, where strait lines meet.

Summary v. Correlation. v. Bi-variate distribution. v. Testing correlation coefficients. v. Transforming to z. v. Use of correlation.

Summary v. Multiple regression. v. Analysis of variance. v. Forward step-wise regression. v. Polynomial regression. v. Multivariate transformation.

Multiple Experiments Genotype x Environment Interactions