Multivariate EMD Extension of time series analysis to

Multi-variate EMD Extension of time series analysis to multi-variable sets

Multivariate • Multivariate is not multi-dimension. • Multivariate variable could be a collection of totally different signals; it could be related ones too: for example, the three components of a velocity vector. • It is useful for image fusion as the three colors of a color picture.

History • Tanaka and Mandic first initiated complex, and Rilling et al bivariate EMD. – Tanaka, T. & Mandic, D. P. 2006 Complex empirical mode decomposition. IEEE Signal Process. Lett. 14, 101– 104. – Rilling, G. , P. Flandrin, P. Gonçalves, and J. M. Lilly, 2007: Bivariate Empirical Mode Decomposition, IEEE SIGNAL PROCESSING LETTERS, VOL. 14, 936 -939. • Mandic extended it to Tri- and Multi-variate. – N. Rehman, D. P. Mandic, 2009: Empirical Mode Decomposition for Trivariate Signals. IEEE TRANSACTIONS ON SIGNAL PROCESSING, VOL. 58, 1059 -1068. – N. Rehman, D. P. Mandic, 2009: Multivariate empirical mode decomposition. Proc. Roy. Soc. Lond. , doi: 10. 1098/rspa. 2009. 0502 N. – Rehman, D. P. Mandic, 2011: Filter Bank Property of Multivariate Empirical Mode Decomposition. IEEE TRANSACTIONS ON SIGNAL PROCESSING, VOL. 59, 2421 -2426.

Initial Example by Rilling et al. Free Matlab/C codes are available at http: //perso. ens-lyon. fr/patrick. flandrin.

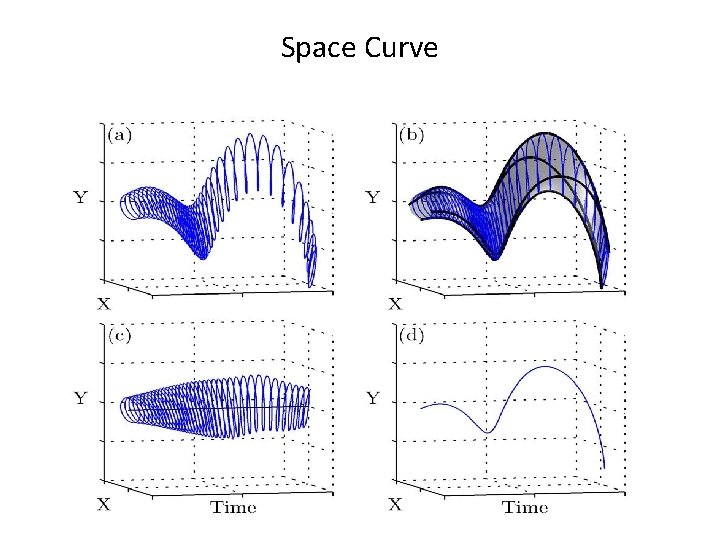
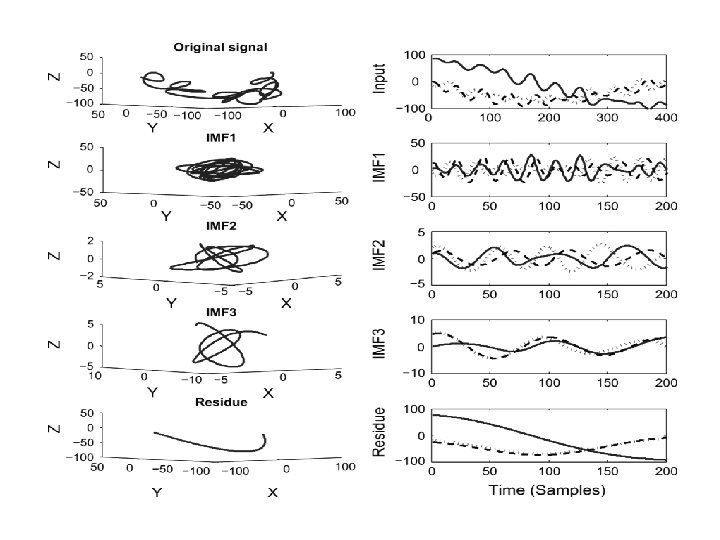
Space Curve

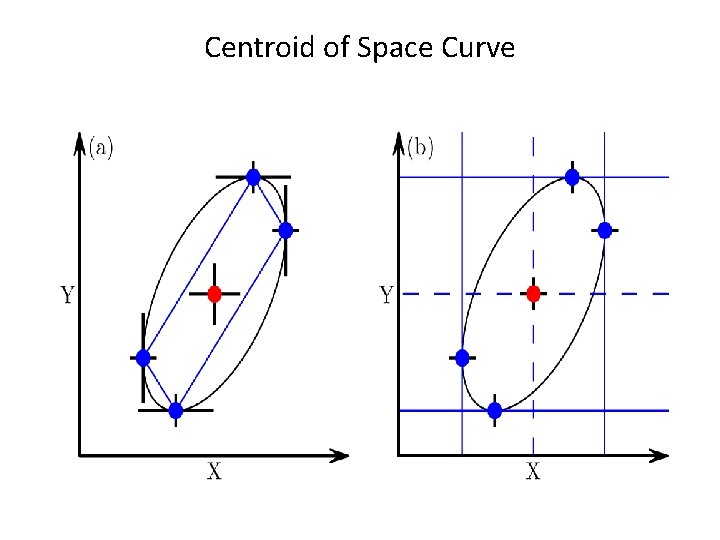
Centroid of Space Curve

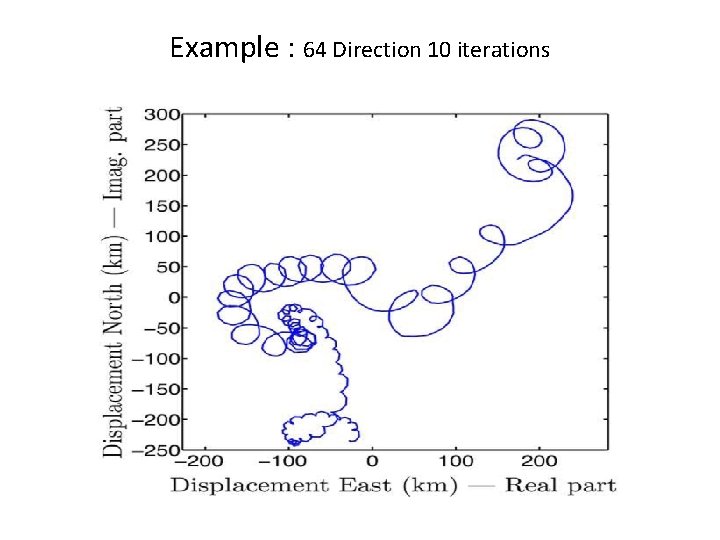
Example : 64 Direction 10 iterations

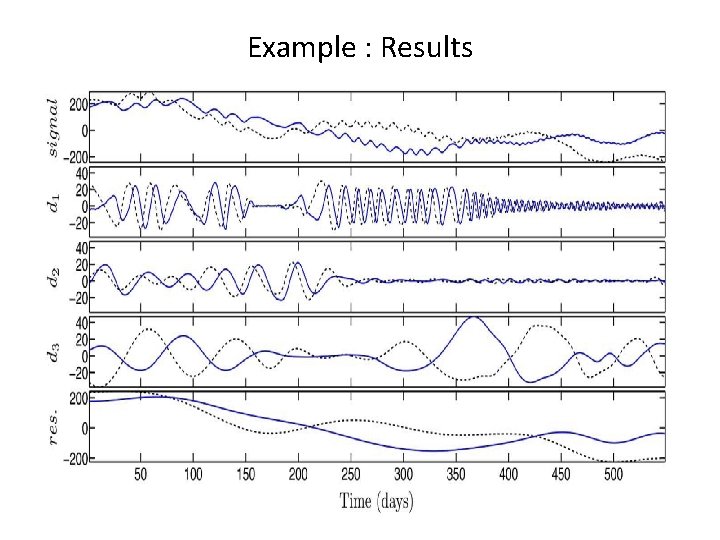
Example : Results

Extension from Bivariate to Tri- and Multivariate is non-trivial We need a new mathematical tool: Quaternion and beyond

Technical prerequisites • Defining the local extrema for multivariate signals is not straightforward; for instance, the complex and quaternion fields are not ordered : using multiple realvalued projections of the signal; the extrema of such projected signals are then interpolated componentwise to yield the multidimensional envelopes of the signal. • The computation of the local mean for multivariate signals: to use real-valued projections along multiple directions on hyperspheres (n-spheres) in order to calculate the envelopes and the local mean of multivariate signals. • To generate a suitable set of direction vectors, unit hyperspheres are sampled based on both uniform angular sampling methods and quasi-Monte Carlo-

3 D Data • For simple 3 D data plus time, we need the quaternion with algebra well developed. • The quaternions are a number system that extends the complex numbers to higher dimensions. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in 3 D space. To extend it to multi dimension is very complicated.

Quaternion Mathematics: Any number of the form q = a + bi + cj + dk where a, b, c, and d are real numbers, i 2 = j 2 =k 2 =-1, and ij =k= -ji, jk=i and ki=j; Under addition and multiplication, quaternions have all the properties of a field, except multiplication is not commutative.

Quaternion Memorial • Broom Bridge, also known as Brougham Bridge, is a bridge along Broombridge Road which crosses the Royal Canal in Cabra, Dublin, Ireland. • Here as he walked by on the 16 th of October 1843 Sir William Rowan Hamilton in a flash of genius discovered the fundamental formula for quaternion multiplication i² = j² = k² = ijk = − 1 & cut it on a stone of this bridge.

Quaternion Memorial

Quaternion Memorial

Rotation

Generalized to n-Dimension • For multivariate signals, the local maxima and minima may not be defined directly. • Moreover, the notion of ‘oscillatory modes’ defining an IMF is rather confusing for multivariate signals. • To deal with these problems, Rehman and Mandic (2009) proposed to generate multiple ndimensional envelopes by taking signal projections along different directions in ndimensional spaces; these are then averaged to obtain the local mean.

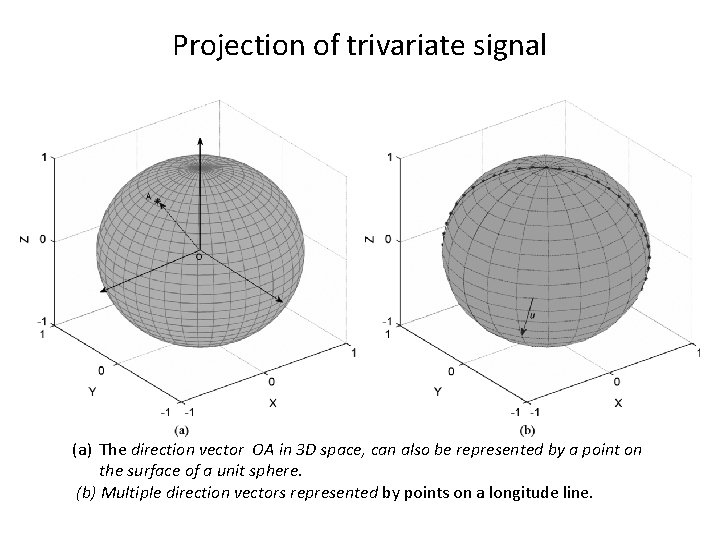
Projection of trivariate signal (a) The direction vector OA in 3 D space, can also be represented by a point on the surface of a unit sphere. (b) Multiple direction vectors represented by points on a longitude line.

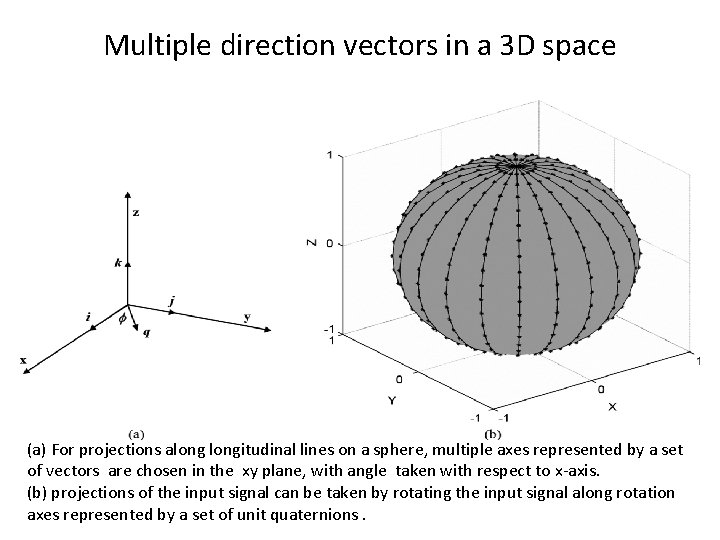
Multiple direction vectors in a 3 D space (a) For projections alongitudinal lines on a sphere, multiple axes represented by a set of vectors are chosen in the xy plane, with angle taken with respect to x-axis. (b) projections of the input signal can be taken by rotating the input signal along rotation axes represented by a set of unit quaternions.

n-Dimensional Case • A simple and practically convenient choice for a set of direction vectors is to employ uniform angular sampling of a unit sphere in an ndimensional hyperspherical coordinate system. The resulting set of direction vectors covers the whole (n − 1) sphere. • A coordinate system in an n-dimensional Euclidean space can then be defined to serve as a pointset (and the corresponding set of direction vectors) on an (n − 1) sphere.

Generalization to n-dimension case Let {θ 1, θ 2, . . . , θ(n− 1)} be the (n − 1) angular coordinates, then an n-dimensional coordinate system having as the n coordinates on a unit (n − 1) sphere is given by

Generalization to n-dimension case • The pointset corresponding to the n-dimensional coordinate system is now very convenient to generate; however, for n >1, it does not provide a uniform sampling distribution having a higher density of the points when approaching the poles. • • Proposed a quasi-Monte Carlo methods to generate a ‘low discrepancy pointset’, providing a more uniform distribution on the n sphere.

Low Discrepancy Sampling • By definition, the discrepancy of a sequence is low if the number of points in the sequence falling into an arbitrary set B and it is close to uniform distribution. • A low-discrepancy sequence is a sequence with the property that for all values of N, its subsequence x 1, . . . , x. N has a low discrepancy. • Low-discrepancy sequences are also called quasirandom or sub-random sequences, due to their common use as a replacement of uniformly distributed random numbers.

Low Discrepancy Sampling • The "quasi" modifier is used to denote more clearly that the values of a low-discrepancy sequence are neither random nor pseudorandom, but such sequences share some properties of random variables. • There are many ways to generate such sequence. In certain applications such as the quasi-Monte Carlo method their lower discrepancy is an important advantage. • Rehman and Mandic used Hammersley-Halton sequence (involved primary numbers etc) to generate the quasi-Monte Carlo sampling, which is almot uniformly distributed.

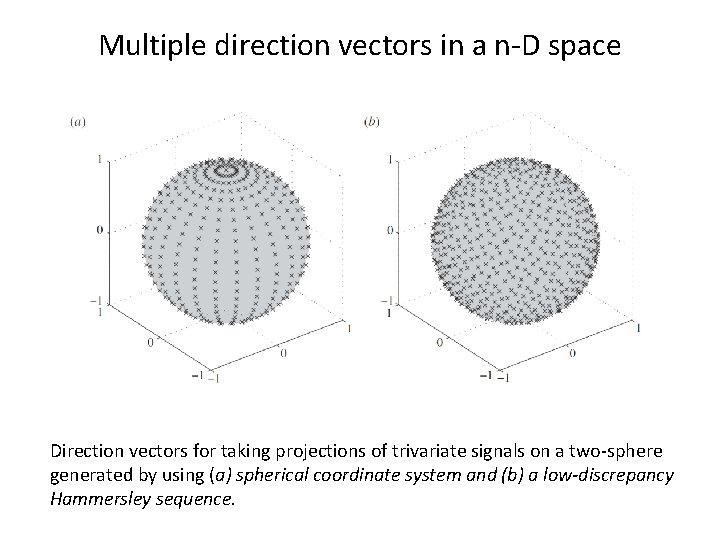
Multiple direction vectors in a n-D space Direction vectors for taking projections of trivariate signals on a two-sphere generated by using (a) spherical coordinate system and (b) a low-discrepancy Hammersley sequence.

Empirical Mode Decomposition, Multivariate EMD, Matlab and data See below for our recent contributions in this field. You can also download EEG Data used in some of the simulations in the work below. The EEG data contain EOG and EMG artifacts coming from eye blinks, eyebrow raising and eye rolling, and are used in our BSE, BSS, and EMD algorithms. The recordings also contain a 50 Hz power line noise. Enjoy! Matlab code: www. commsp. ee. ic. ac. uk/mandic

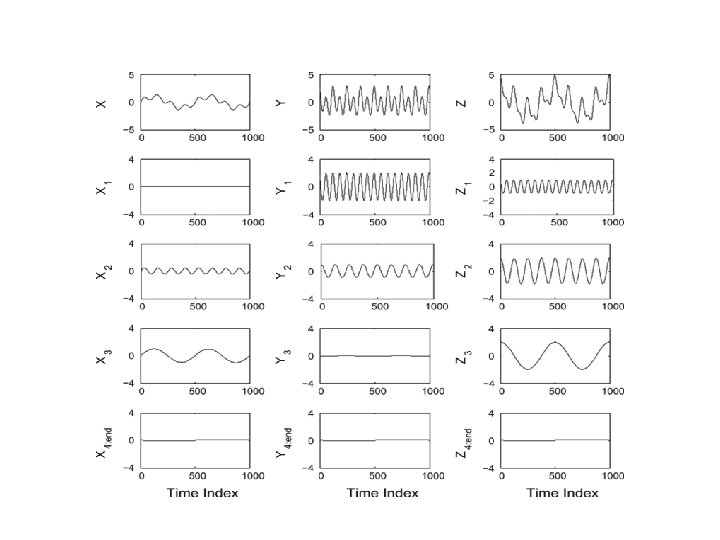
Some examples 3 -Dimensional

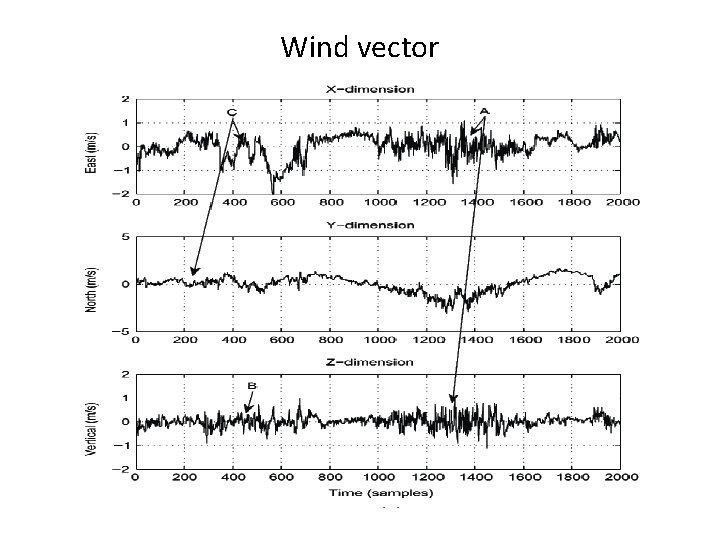
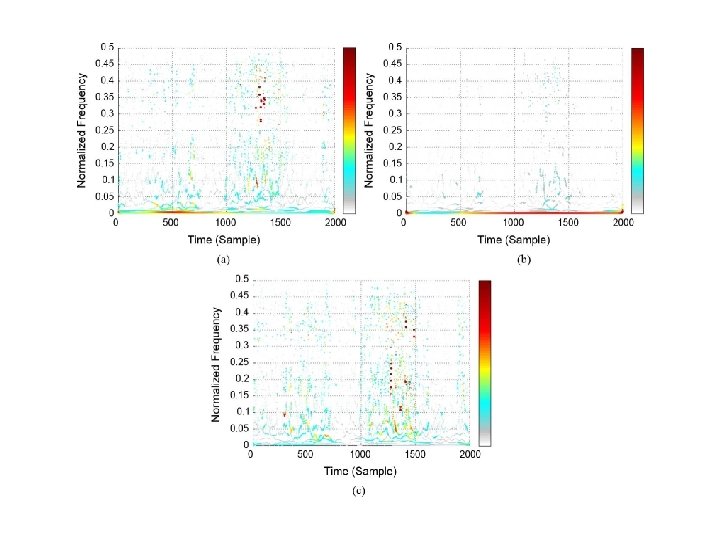
Wind vector

Wind vector

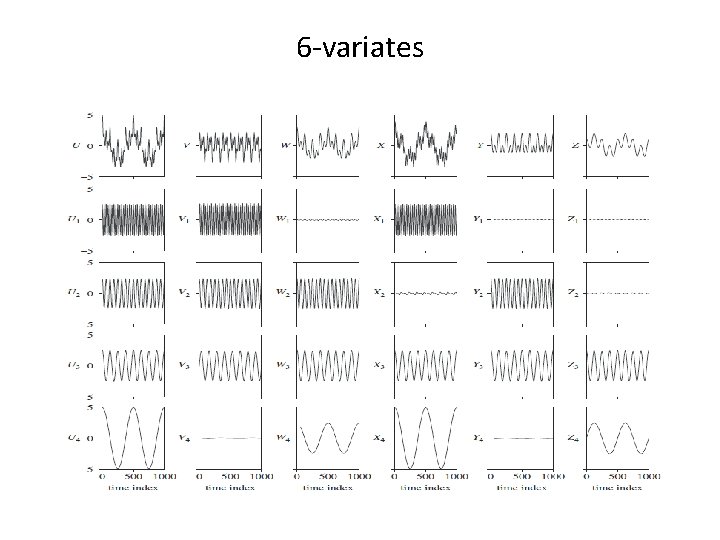
Multi-variate 6 -Dimensional

6 -variates

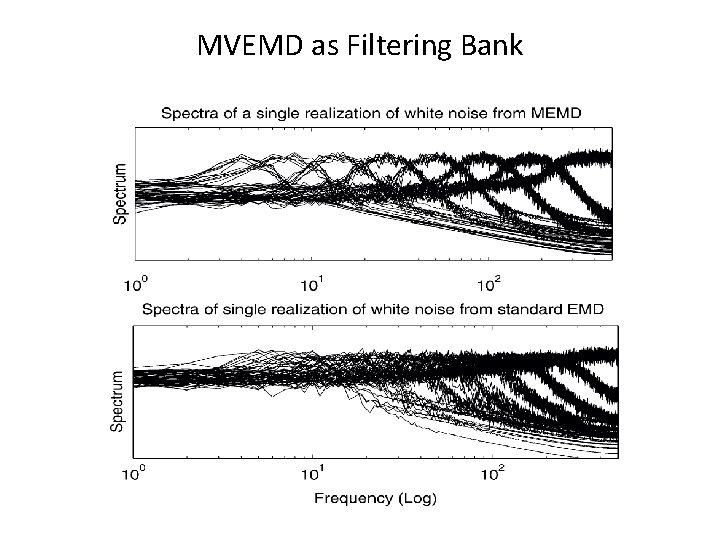
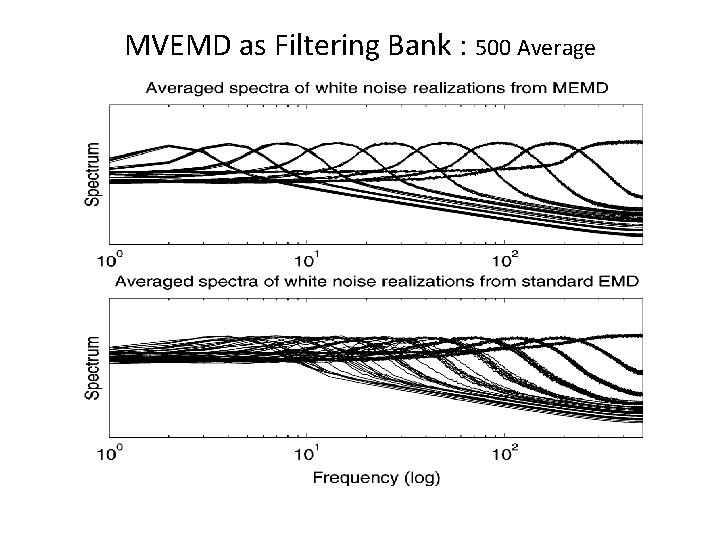
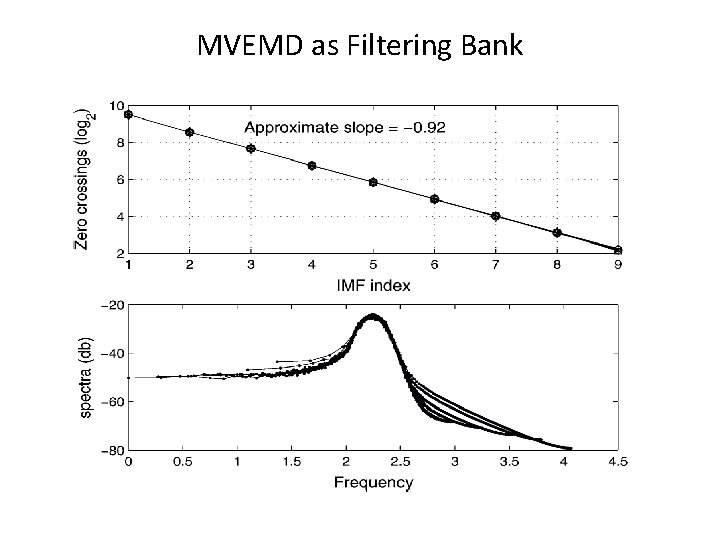
As a Filtering Bank Rehman, N and D. P. Mandic, 2011: Filter Bank Property of Multivariate Empirical Mode Decomposition. IEEE Transactions on Signal Processing, vol. 59, 24212426

MVEMD as Filtering Bank

MVEMD as Filtering Bank : 500 Average

MVEMD as Filtering Bank

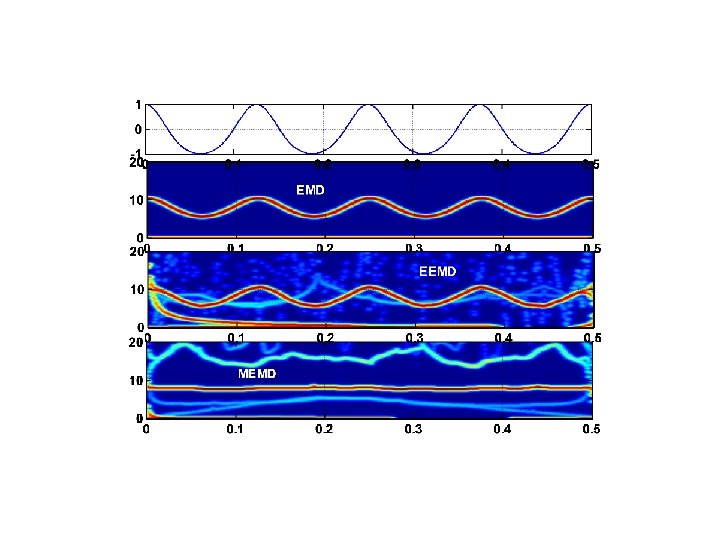
Observations • MVEMD indeed is a super-filter bank. • The filter is much sharper than EMD as shown. • Unfortunately, the sharpness of the filter bank has a fatal flaw: it could strip the harmonics off a nonlinear signal. See example.

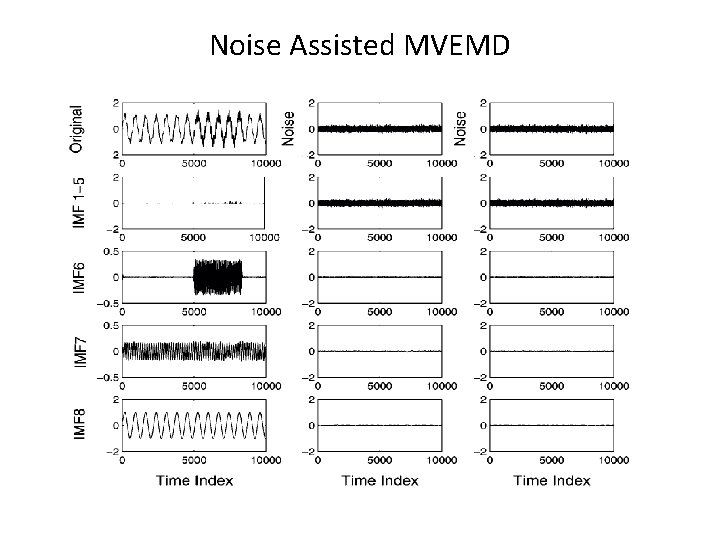
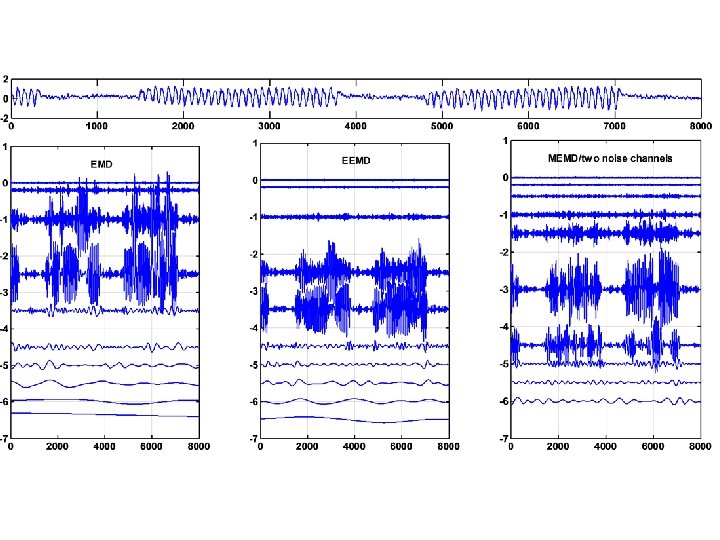
It is possible to implement Noise Assisted MVEMD Adding several noise signals as additional variates to the real data to form a multivariate data set. N. B. the data never mixed with the noises.

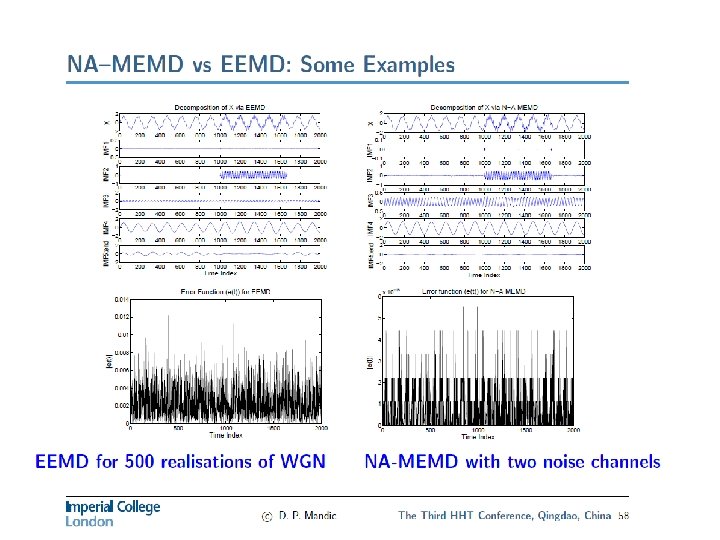
Noise Assisted MVEMD

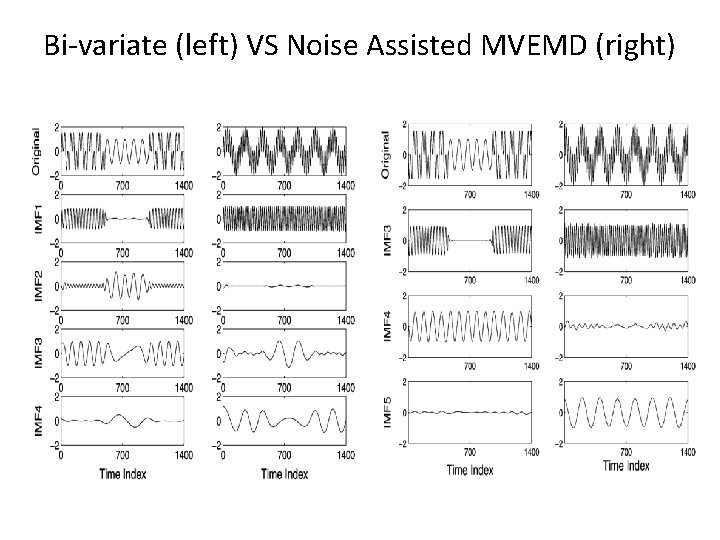
Bi-variate (left) VS Noise Assisted MVEMD (right)

Effects of noise level and sharpness of the filter

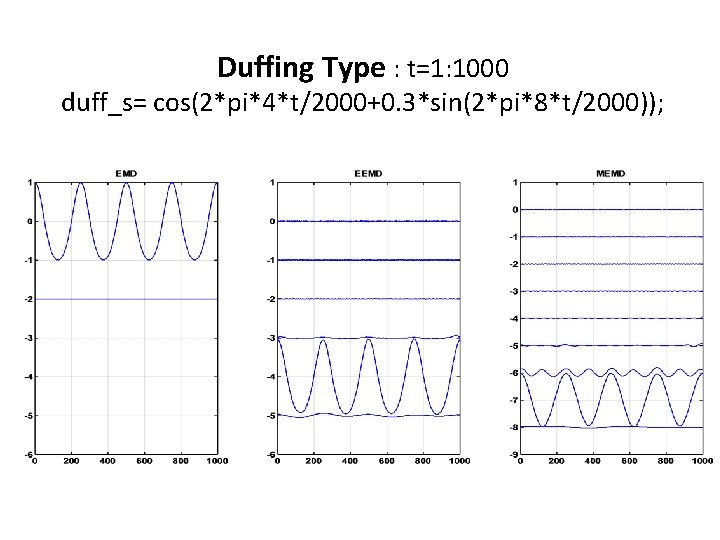
Duffing Type : t=1: 1000 duff_s= cos(2*pi*4*t/2000+0. 3*sin(2*pi*8*t/2000));

NA-MVEMD applied on a Duffy signal • MVEMD parameters used: n = 3 (2 extra noise channels) dir = 32; stopping_criteria=‘stop’ ; threshold=[0. 1 1 0. 1] • Power of Duffy signal was set to 1, and the power (variance) of two noise channels was varied to get a range of SNR = 10 log (P duffy/P noise) values. • NA-MVEMD has been shown to perform well for a range of SNR values but for lower SNR (higher noise power), the obtained decomposition for this input signal is not very accurate. • In NA-MVEMD, increase in the noise power tends to enforce filter bank structure on the input signal. In such cases NA-MVEMD will decompose a nonlinear signal with its harmonics across multiple IMFs.

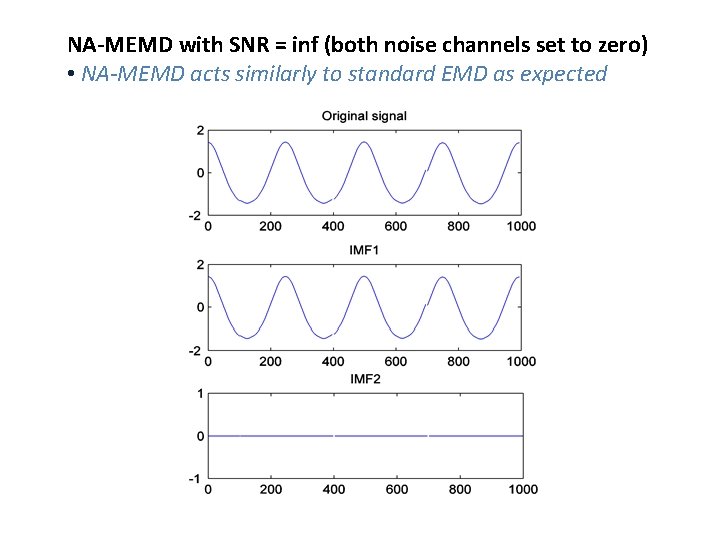
NA-MEMD with SNR = inf (both noise channels set to zero) • NA-MEMD acts similarly to standard EMD as expected

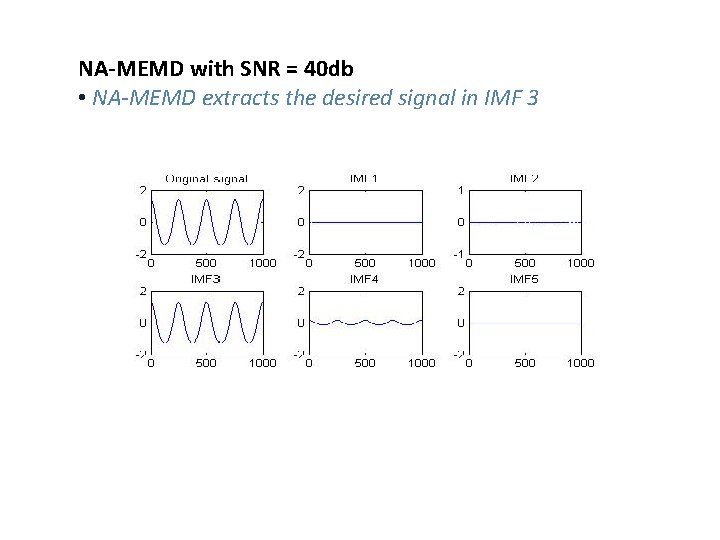
NA-MEMD with SNR = 40 db • NA-MEMD extracts the desired signal in IMF 3

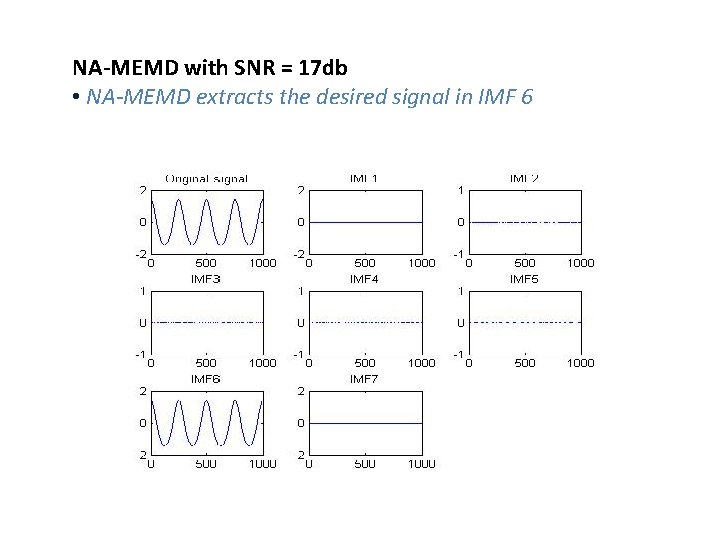
NA-MEMD with SNR = 17 db • NA-MEMD extracts the desired signal in IMF 6

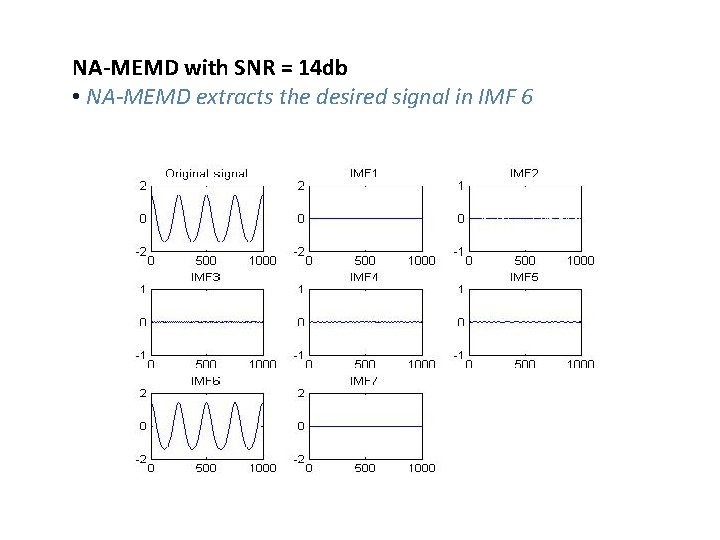
NA-MEMD with SNR = 14 db • NA-MEMD extracts the desired signal in IMF 6

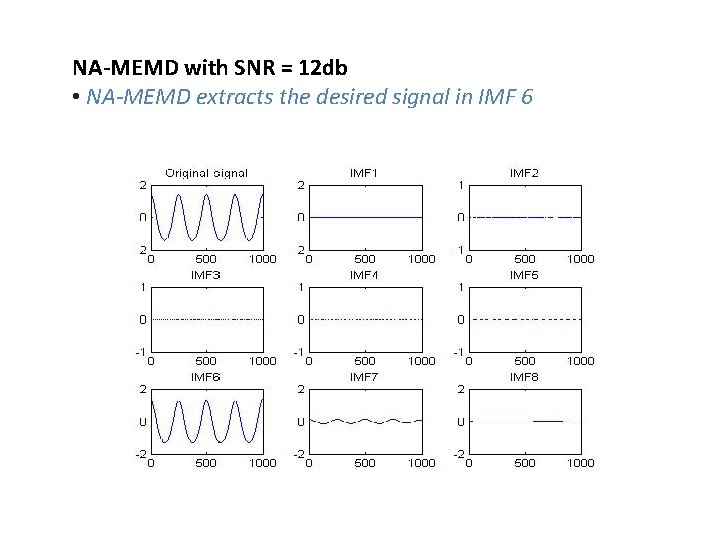
NA-MEMD with SNR = 12 db • NA-MEMD extracts the desired signal in IMF 6

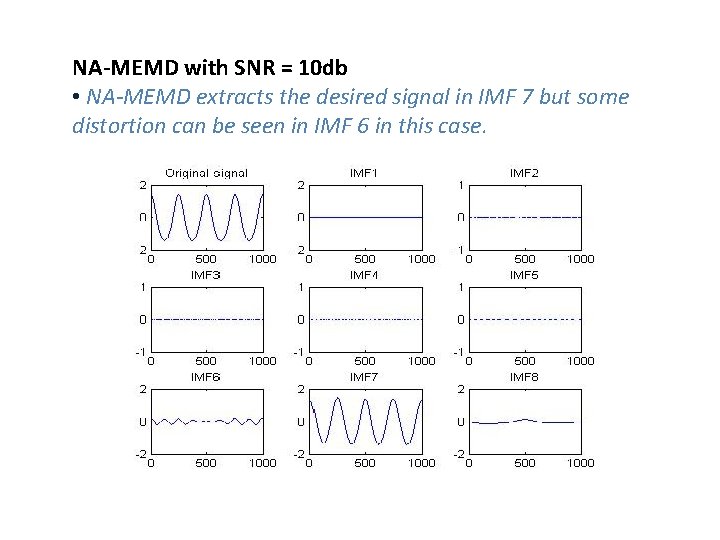
NA-MEMD with SNR = 10 db • NA-MEMD extracts the desired signal in IMF 7 but some distortion can be seen in IMF 6 in this case.

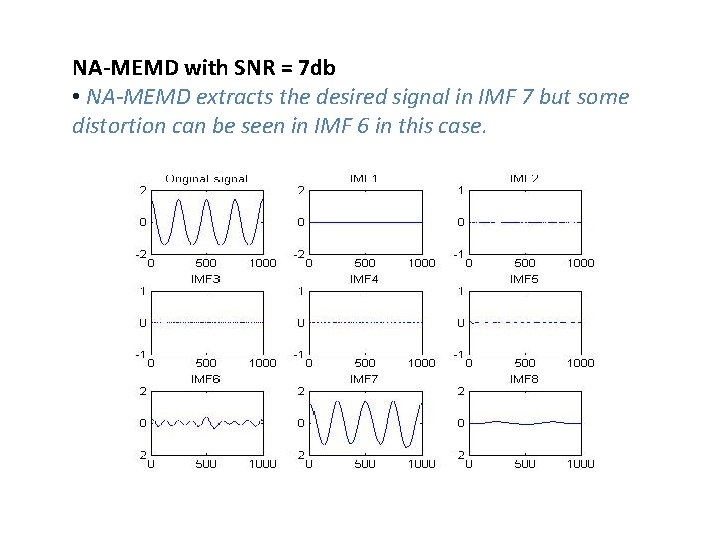
NA-MEMD with SNR = 7 db • NA-MEMD extracts the desired signal in IMF 7 but some distortion can be seen in IMF 6 in this case.

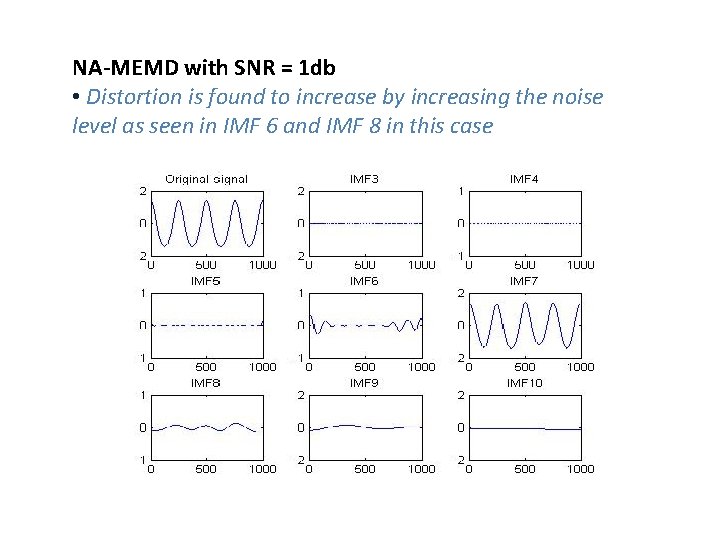
NA-MEMD with SNR = 1 db • Distortion is found to increase by increasing the noise level as seen in IMF 6 and IMF 8 in this case

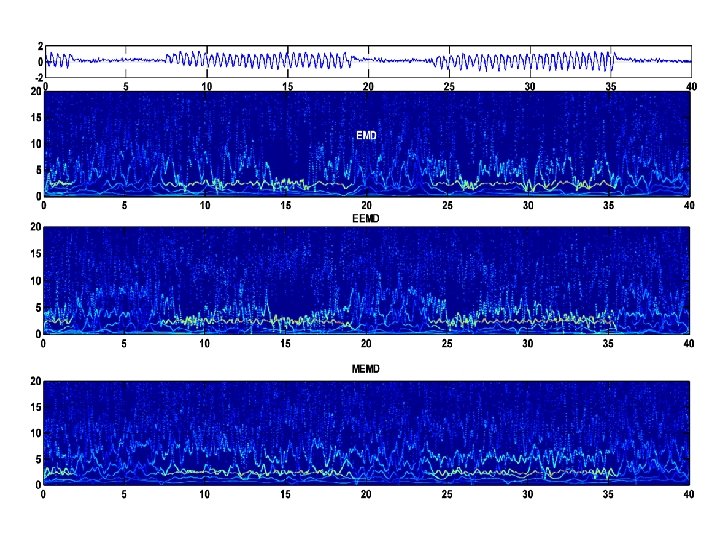
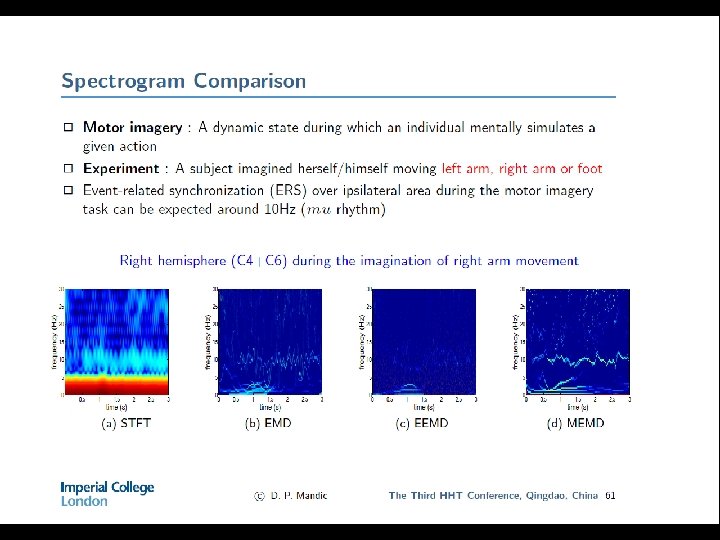
Application to EEG

Summary • MVEMD is a very useful and intriguing new development in EMD methodology. • It offers an uniformity (same scale and same number) to the IMF from the multivariate data set so that the results will be easier to interpret. • The NA-MVEMD is a beautiful idea. • The fatal flaw of MVEMD and NA-MVEMD is that the filter is too sharp, which leads to separation of harmonics from the fundamental and destroy the nonlinearity.