Multivariate Data Descriptive techniques for Multivariate data In













































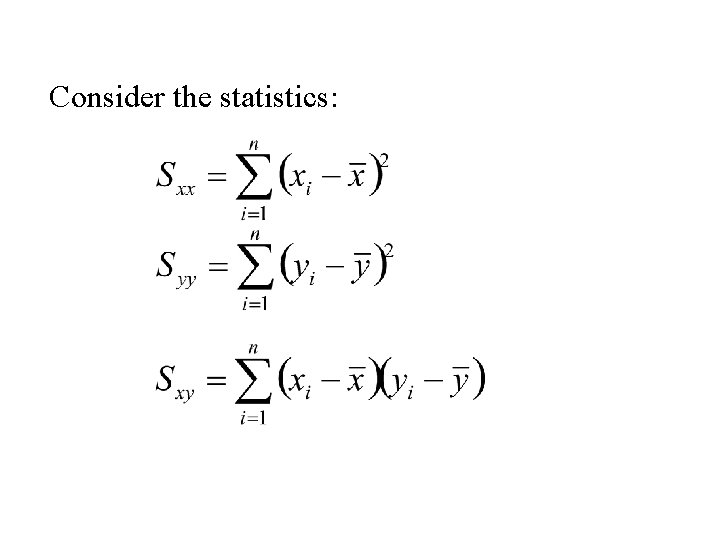

















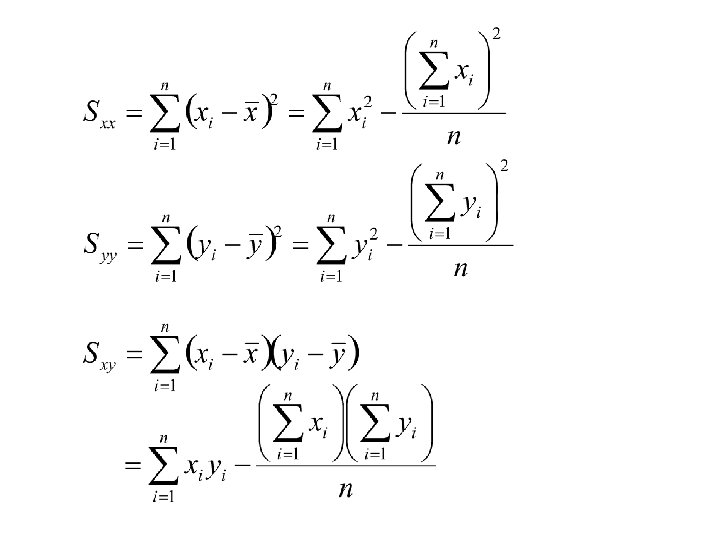




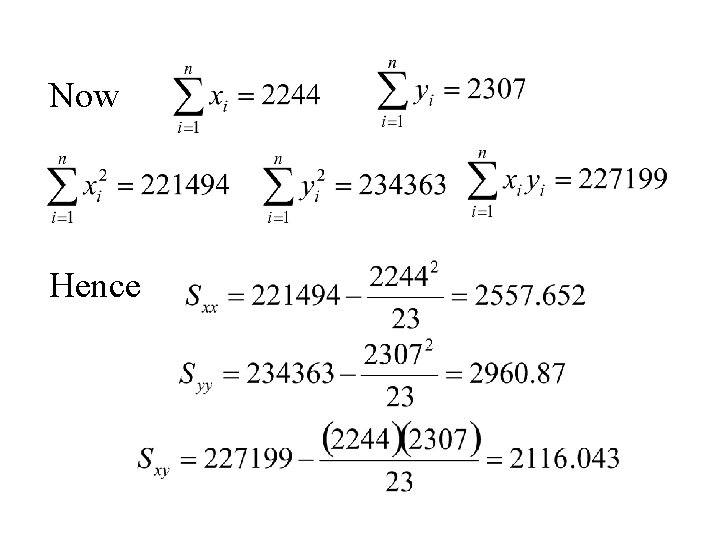















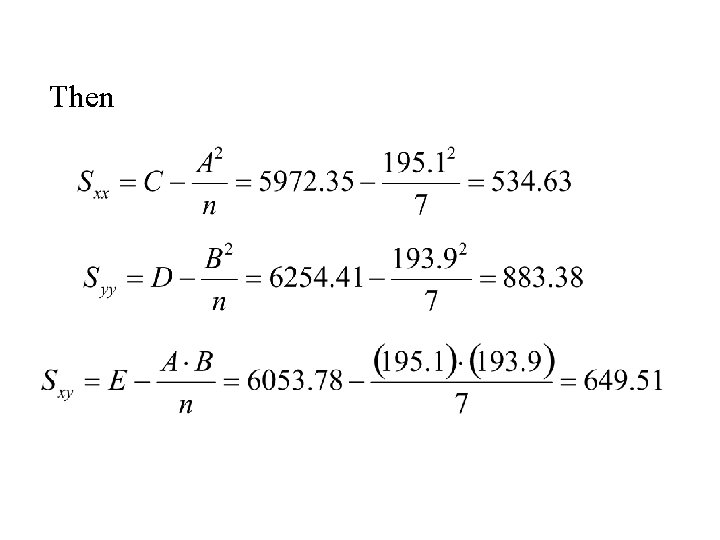

























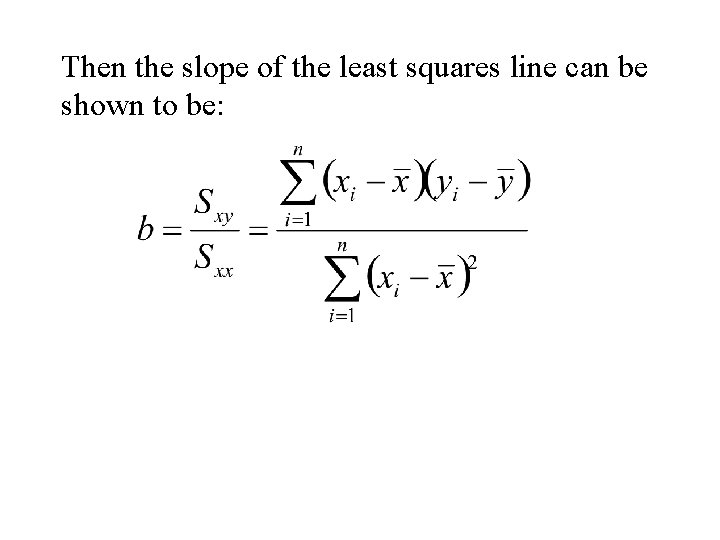

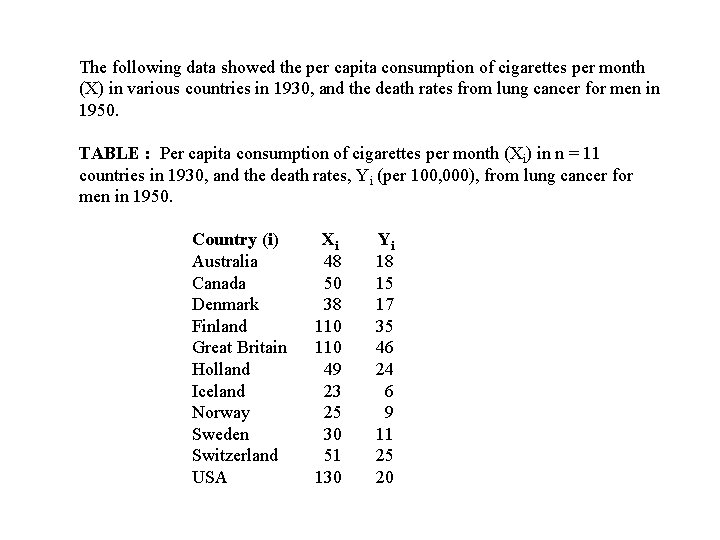

















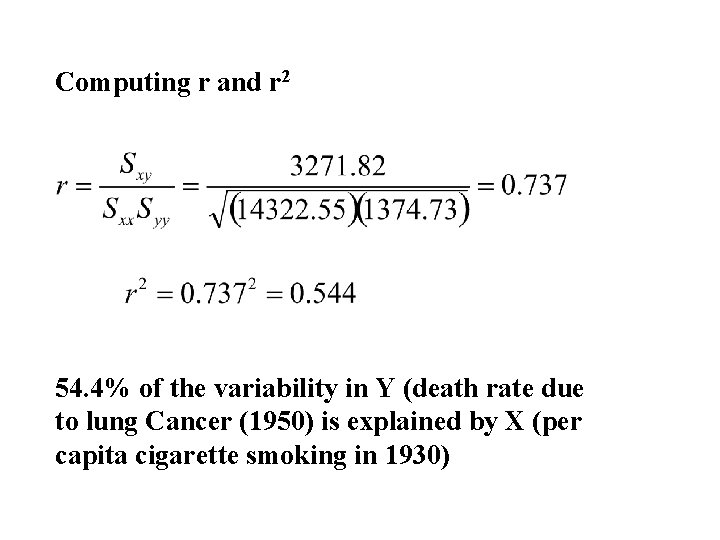


- Slides: 167

Multivariate Data

Descriptive techniques for Multivariate data In most research situations data is collected on more than one variable (usually many variables)

Graphical Techniques • The scatter plot • The two dimensional Histogram

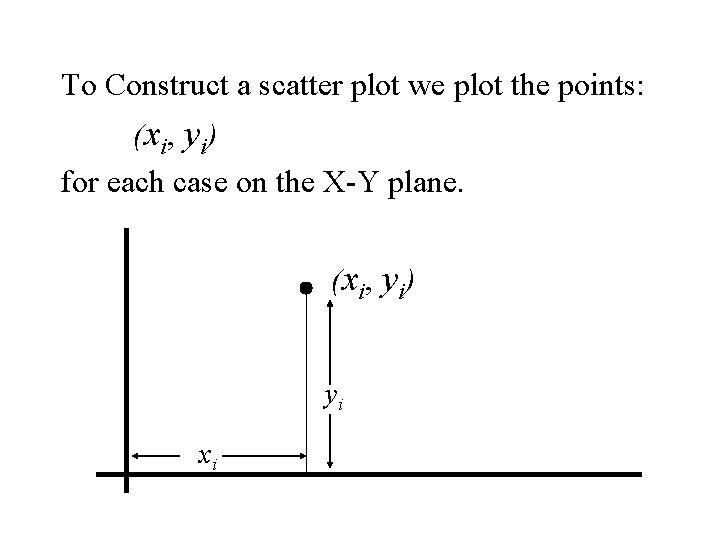
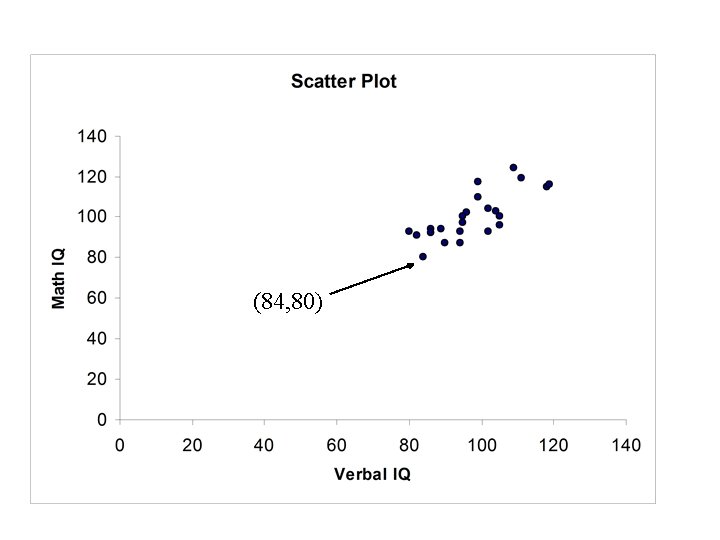
The Scatter Plot For two variables X and Y we will have a measurements for each variable on each case: xi, yi xi = the value of X for case i and yi = the value of Y for case i.

To Construct a scatter plot we plot the points: (xi, yi) for each case on the X-Y plane. (xi, yi) yi xi

Student Verbal IQ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 86 104 86 105 118 96 90 95 105 84 94 119 82 80 109 111 89 99 94 99 95 102 Data Set #3 The following table gives data on Verbal IQ, Math IQ, Initial Reading Acheivement Score, and Final Reading Acheivement Score for 23 students who have recently completed a reading improvement program Initial Final Math Reading IQ Acheivement 94 103 92 100 115 102 87 100 96 80 87 116 91 93 124 119 94 117 93 110 97 104 93 1. 1 1. 5 2. 0 1. 9 1. 4 1. 5 1. 4 1. 7 1. 6 1. 7 1. 2 1. 0 1. 8 1. 4 1. 6 1. 4 1. 5 1. 7 1. 6 1. 7 1. 9 2. 0 3. 5 2. 4 1. 8 2. 0 1. 7 3. 1 1. 8 1. 7 2. 5 3. 0 1. 8 2. 6 1. 4 2. 0 1. 3 3. 1 1. 9


(84, 80)


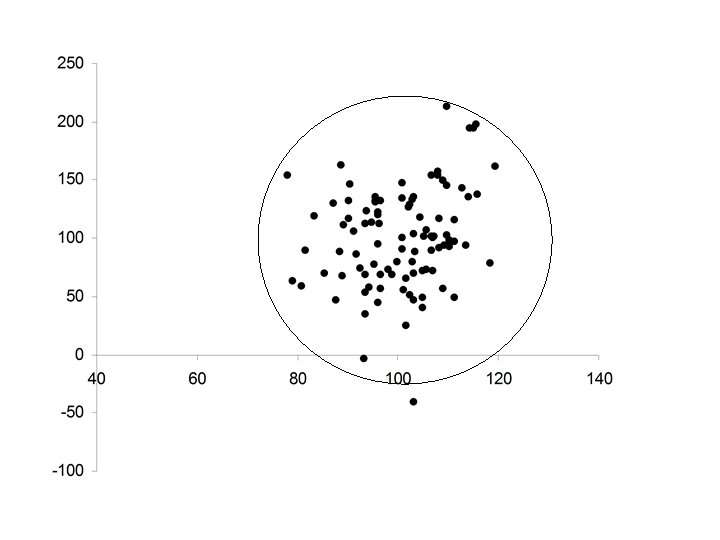
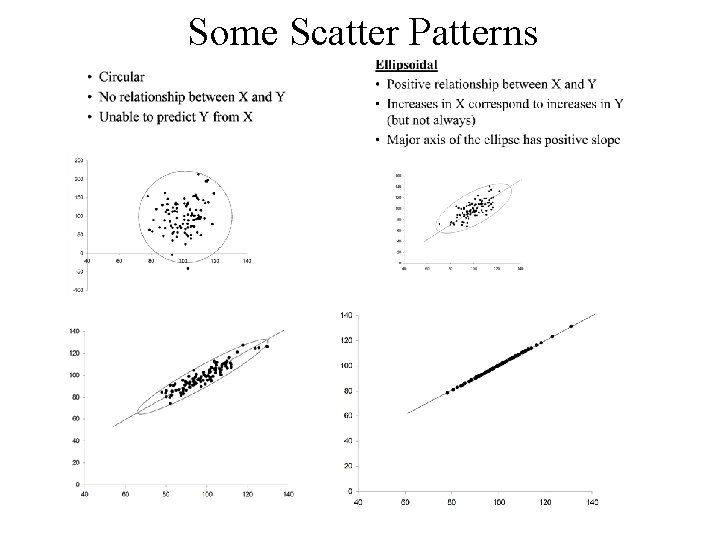
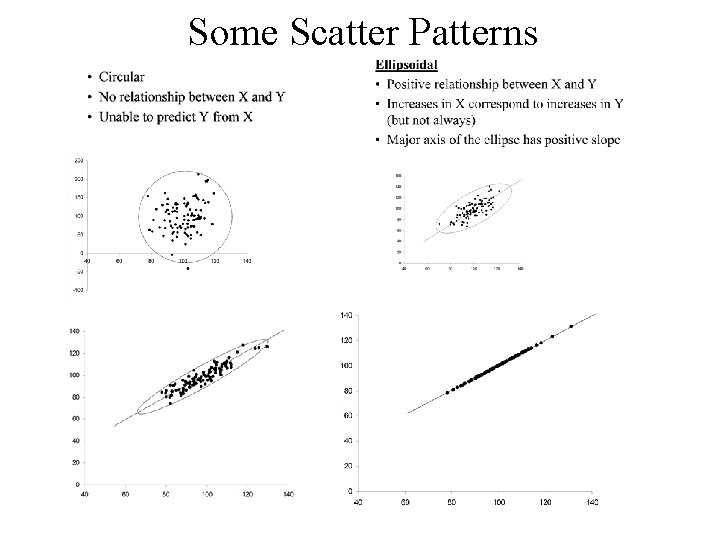
Some Scatter Patterns



• Circular • No relationship between X and Y • Unable to predict Y from X



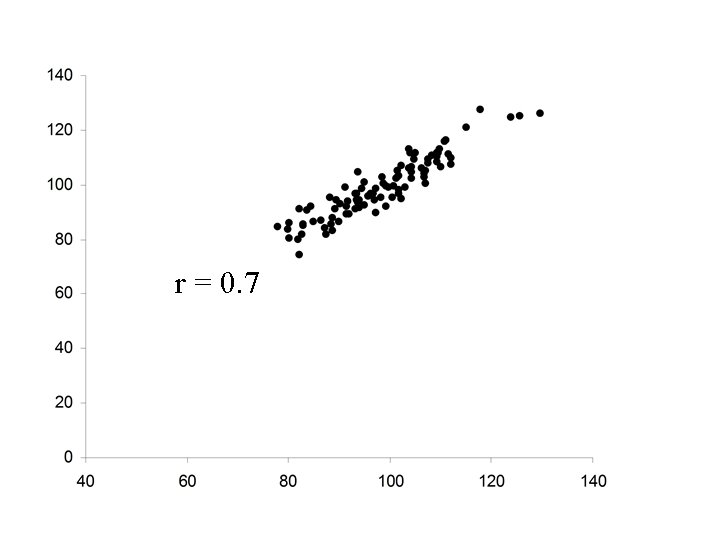
• Ellipsoidal • Positive relationship between X and Y • Increases in X correspond to increases in Y (but not always) • Major axis of the ellipse has positive slope


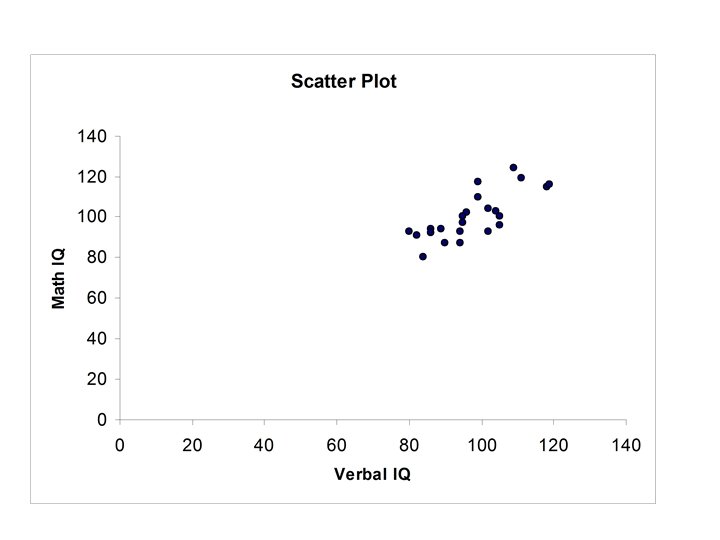
Example Verbal IQ, Math. IQ


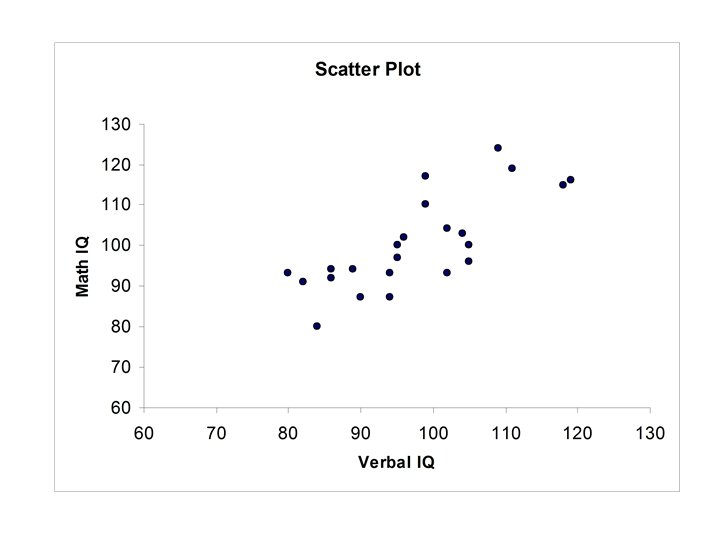
Some More Patterns



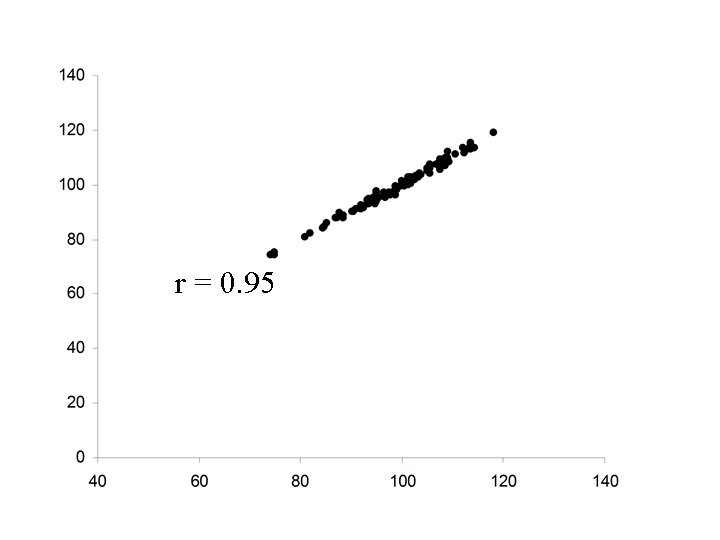
• Ellipsoidal (thinner ellipse) • Stronger positive relationship between X and Y • Increases in X correspond to increases in Y (more freqequently) • Major axis of the ellipse has positive slope • Minor axis of the ellipse much smaller


• Increased strength in the positive relationship between X and Y • Increases in X correspond to increases in Y (almost always) • Minor axis of the ellipse extremely small in relationship to the Major axis of the ellipse.



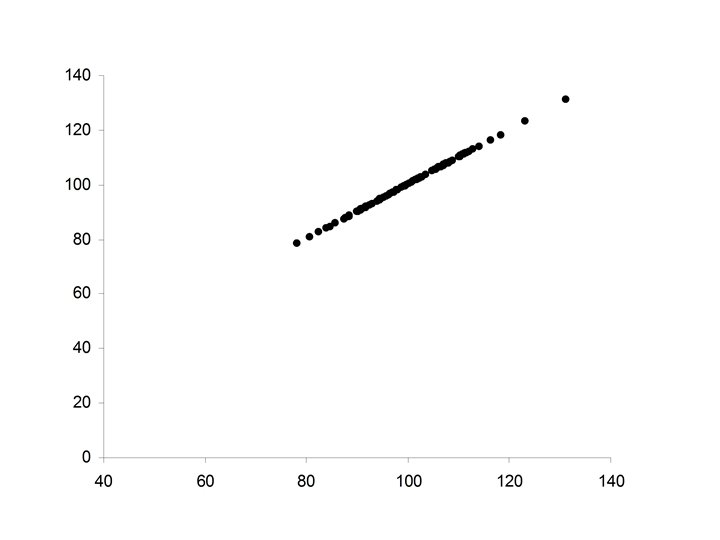
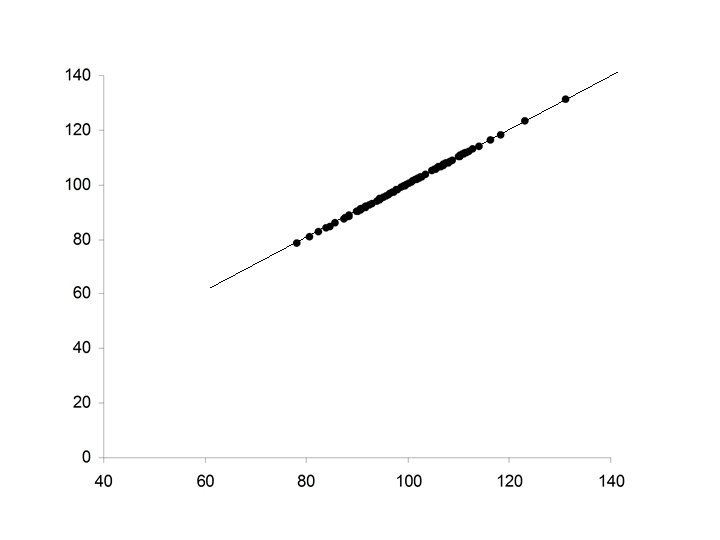
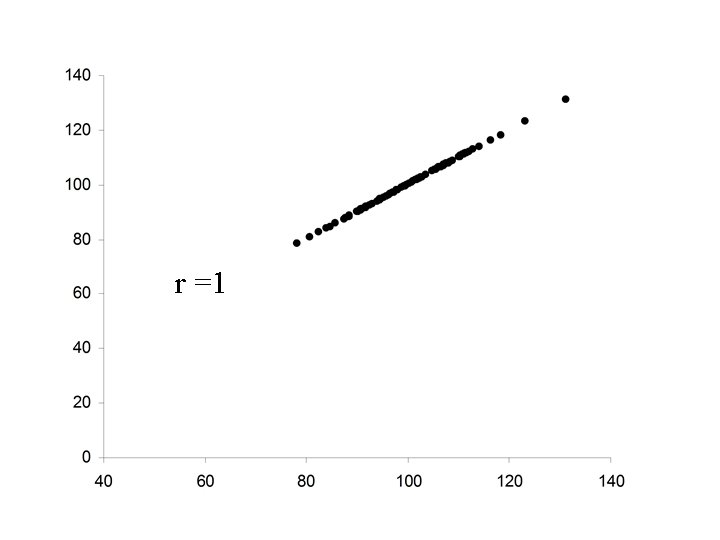
• Perfect positive relationship between X and Y • Y perfectly predictable from X • Data falls exactly along a straight line with positive slope



• Ellipsoidal • Negative relationship between X and Y • Increases in X correspond to decreases in Y (but not always) • Major axis of the ellipse has negative slope


• The strength of the relationship can increase until changes in Y can be perfectly predicted from X






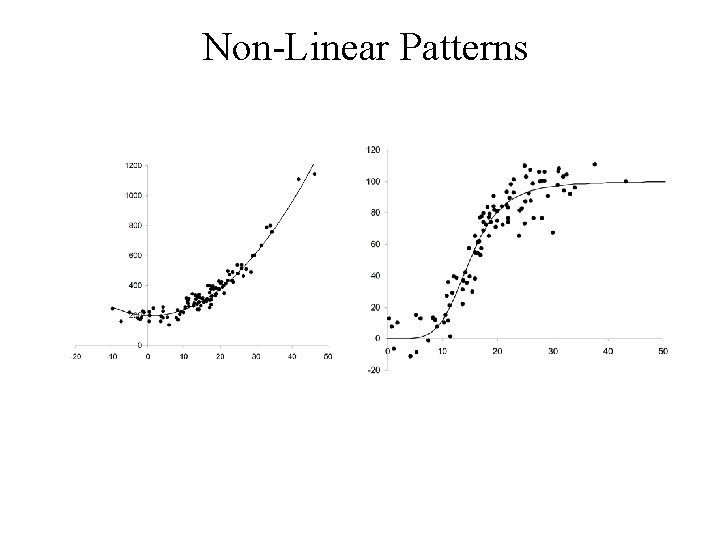
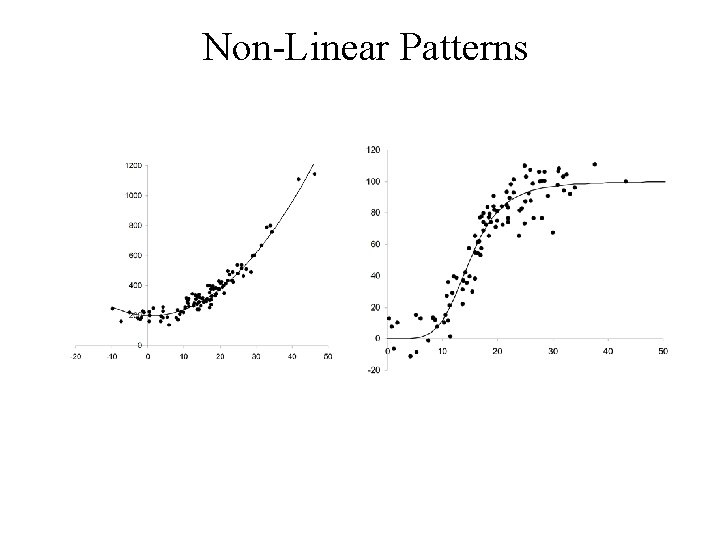
Some Non-Linear Patterns



• In a Linear pattern Y increase with respect to X at a constant rate • In a Non-linear pattern the rate that Y increases with respect to X is variable

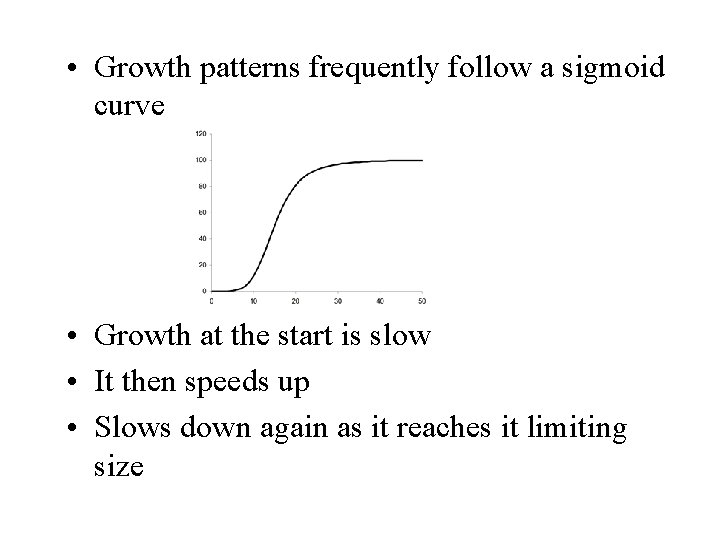
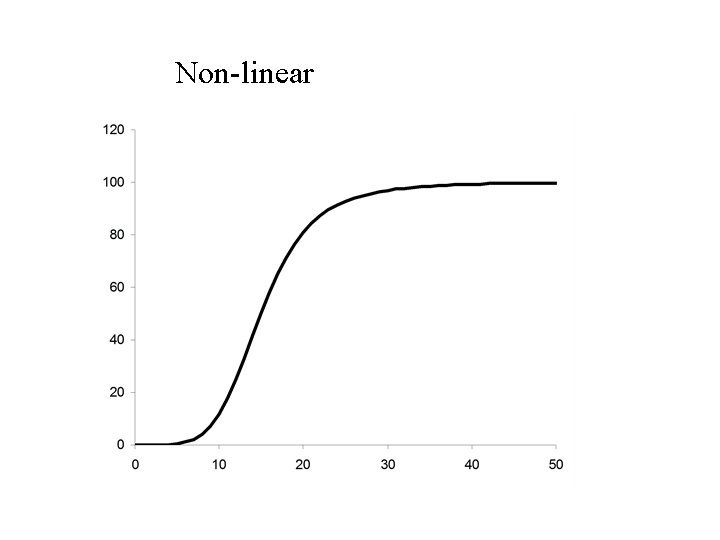
Growth Patterns



• Growth patterns frequently follow a sigmoid curve • Growth at the start is slow • It then speeds up • Slows down again as it reaches it limiting size

Review the scatter plot

Some Scatter Patterns


Non-Linear Patterns

Measures of strength of a relationship (Correlation) • Pearson’s correlation coefficient (r) • Spearman’s rank correlation coefficient (rho, r)

Assume that we have collected data on two variables X and Y. Let (x 1, y 1) (x 2, y 2) (x 3, y 3) … (xn, yn) denote the pairs of measurements on the on two variables X and Y for n cases in a sample (or population)

From this data we can compute summary statistics for each variable. The means and

The standard deviations and

These statistics: • give information for each variable separately but • give no information about the relationship between the two variables
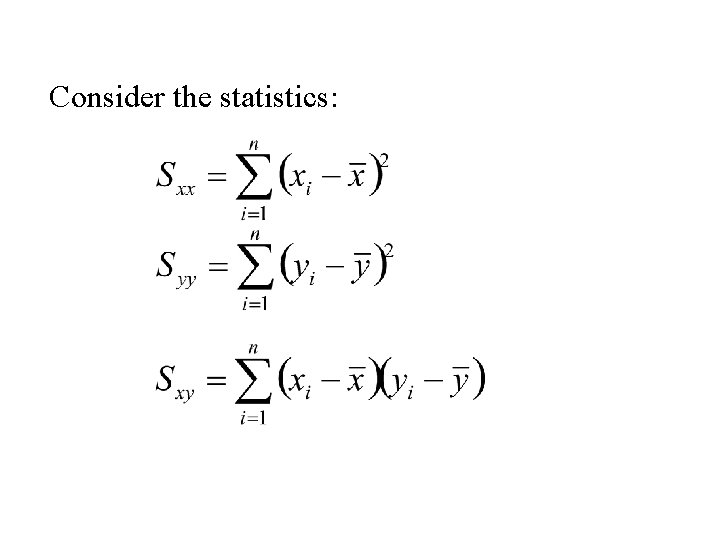
Consider the statistics:

The first two statistics: and • are used to measure variability in each variable • they are used to compute the sample standard deviations

The third statistic: • is used to measure correlation • If two variables are positively related the sign of will agree with the sign of

• When is positive will be positive. • When xi is above its mean, yi will be above its mean • When is negative will be negative. • When xi is below its mean, yi will be below its mean The product will be positive for most cases.


This implies that the statistic • will be positive • Most of the terms in this sum will be positive

On the other hand • If two variables are negatively related the sign of will be opposite in sign to

• When is positive will be negative. • When xi is above its mean, yi will be below its mean • When is negative will be positive. • When xi is below its mean, yi will be above its mean The product will be negative for most cases.

Again implies that the statistic • will be negative • Most of the terms in this sum will be negative

Pearsons correlation coefficient is defined as below:

The denominator: is always positive

The numerator: • is positive if there is a positive relationship between X ad Y and • negative if there is a negative relationship between X ad Y. • This property carries over to Pearson’s correlation coefficient r

Properties of Pearson’s correlation coefficient r 1. The value of r is always between – 1 and +1. 2. If the relationship between X and Y is positive, then r will be positive. 3. If the relationship between X and Y is negative, then r will be negative. 4. If there is no relationship between X and Y, then r will be zero. 5. The value of r will be +1 if the points, (xi, yi) lie on a straight line with positive slope. 6. The value of r will be -1 if the points, (xi, yi) lie on a straight line with negative slope.

r =1

r = 0. 95

r = 0. 7

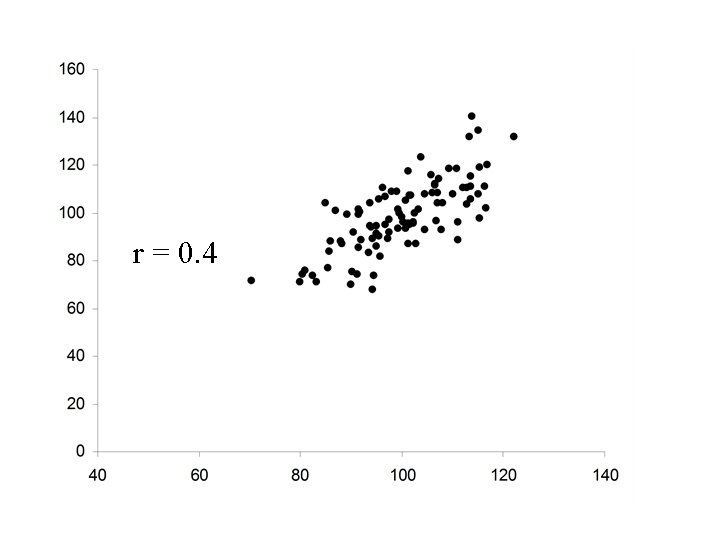
r = 0. 4

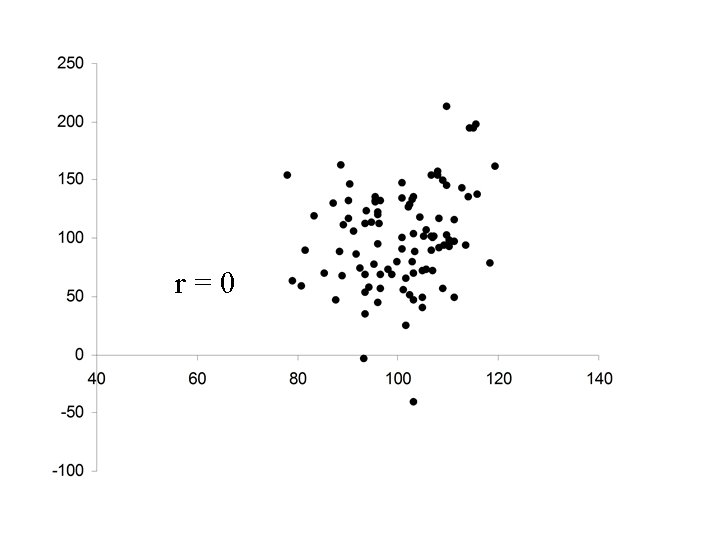
r = 0




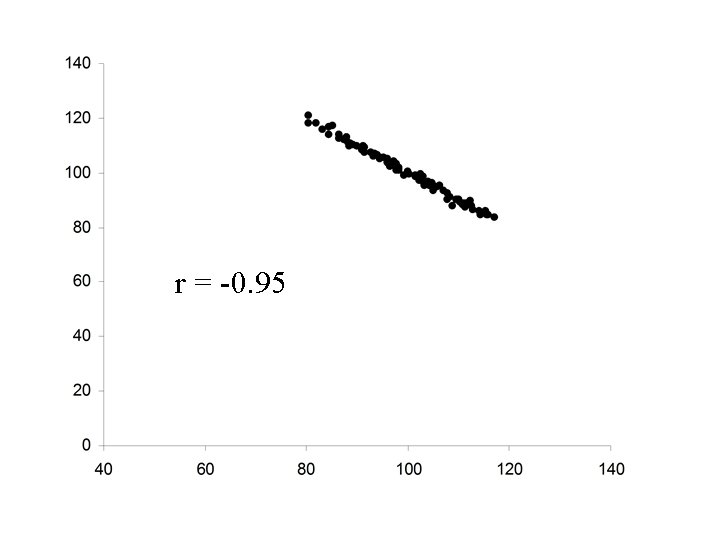
r = -0. 95


Computing formulae for the statistics:
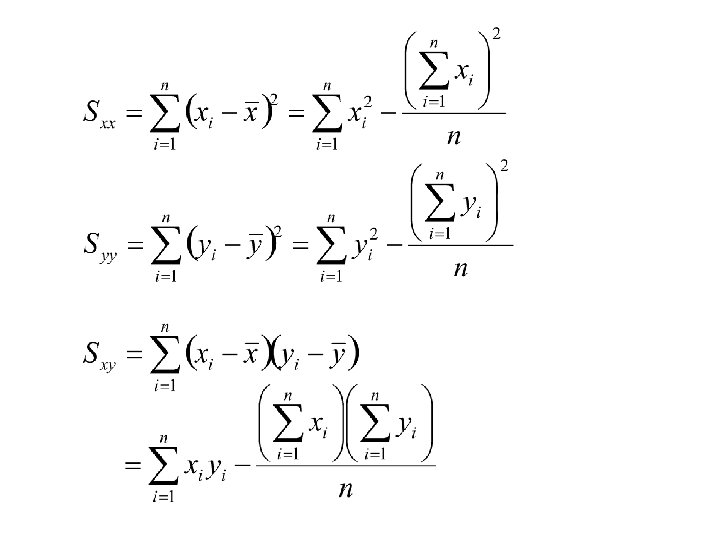

To compute first compute Then

Example Verbal IQ, Math. IQ

Student Verbal IQ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 86 104 86 105 118 96 90 95 105 84 94 119 82 80 109 111 89 99 94 99 95 102 Data Set #3 The following table gives data on Verbal IQ, Math IQ, Initial Reading Acheivement Score, and Final Reading Acheivement Score for 23 students who have recently completed a reading improvement program Initial Final Math Reading IQ Acheivement 94 103 92 100 115 102 87 100 96 80 87 116 91 93 124 119 94 117 93 110 97 104 93 1. 1 1. 5 2. 0 1. 9 1. 4 1. 5 1. 4 1. 7 1. 6 1. 7 1. 2 1. 0 1. 8 1. 4 1. 6 1. 4 1. 5 1. 7 1. 6 1. 7 1. 9 2. 0 3. 5 2. 4 1. 8 2. 0 1. 7 3. 1 1. 8 1. 7 2. 5 3. 0 1. 8 2. 6 1. 4 2. 0 1. 3 3. 1 1. 9

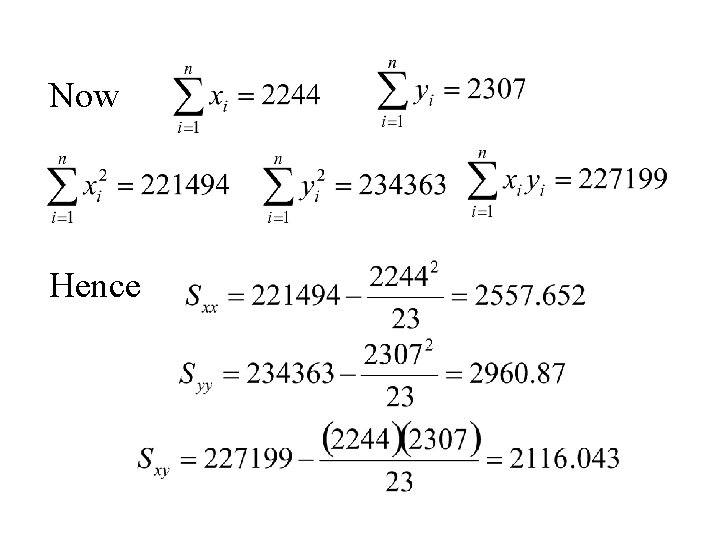
Now Hence

Thus Pearsons correlation coefficient is:

Thus r = 0. 769 • Verbal IQ and Math IQ are positively correlated. • If Verbal IQ is above (below) the mean then for most cases Math IQ will also be above (below) the mean.

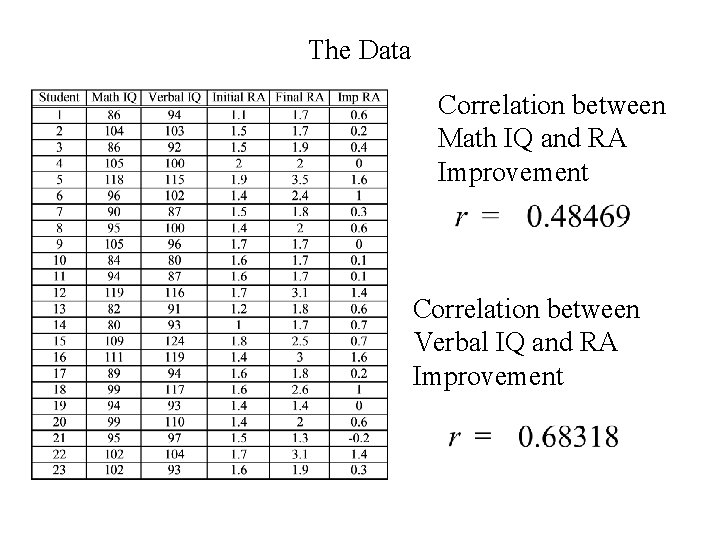
Is the improvement in reading achievement (RA) related to either Verbal IQ or Math IQ? improvement in RA = Final RA – Initial RA

The Data Correlation between Math IQ and RA Improvement Correlation between Verbal IQ and RA Improvement

Scatterplot: Math IQ vs RA Improvement

Scatterplot: Verbal IQ vs RA Improvement

Spearman’s rank correlation coefficient r (rho)

Spearman’s rank correlation coefficient r (rho) Spearman’s rank correlation coefficient is computed as follows: • Arrange the observations on X in increasing order and assign them the ranks 1, 2, 3, …, n • Arrange the observations on Y in increasing order and assign them the ranks 1, 2, 3, …, n. • For any case (i) let (xi, yi) denote the observations on X and Y and let (ri, si) denote the ranks on X and Y.

• If the variables X and Y are strongly positively correlated the ranks on X should generally agree with the ranks on Y. (The largest X should be the largest Y, The smallest X should be the smallest Y). • If the variables X and Y are strongly negatively correlated the ranks on X should in the reverse order to the ranks on Y. (The largest X should be the smallest Y, The smallest X should be the largest Y). • If the variables X and Y are uncorrelated the ranks on X should randomly distributed with the ranks on Y.

Spearman’s rank correlation coefficient is defined as follows: For each case let di = ri – si = difference in the two ranks. Then Spearman’s rank correlation coefficient (r) is defined as follows:

Properties of Spearman’s rank correlation coefficient r 1. The value of r is always between – 1 and +1. 2. If the relationship between X and Y is positive, then r will be positive. 3. If the relationship between X and Y is negative, then r will be negative. 4. If there is no relationship between X and Y, then r will be zero. 5. The value of r will be +1 if the ranks of X completely agree with the ranks of Y. 6. The value of r will be -1 if the ranks of X are in reverse order to the ranks of Y.

Example xi 25. 0 33. 9 16. 7 37. 4 24. 6 17. 3 40. 2 yi 24. 3 38. 7 13. 4 32. 1 28. 0 12. 5 44. 9 Ranking the X’s and the Y’s we get: ri 4 5 1 6 3 2 7 si 3 6 2 5 4 1 7 Computing the differences in ranks gives us: di 1 -1 -1 1 0


Computing Pearsons correlation coefficient, r, for the same problem:


To compute first compute
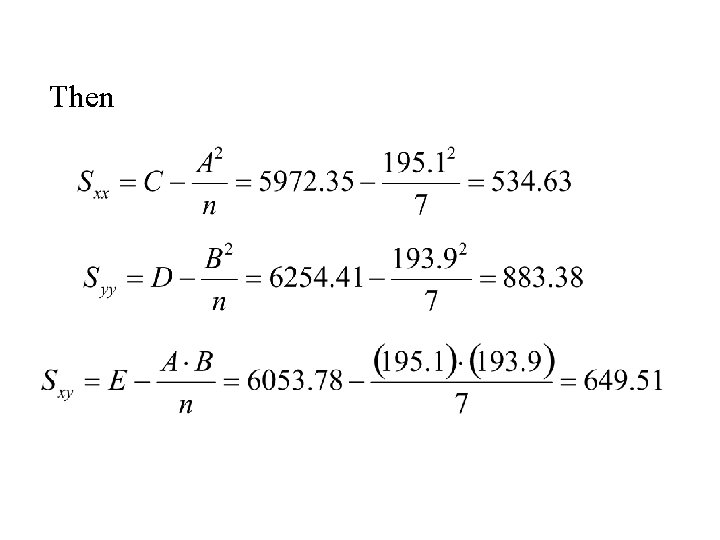
Then

and Compare with

Comments: Spearman’s rank correlation coefficient r and Pearson’s correlation coefficient r 1. The value of r can also be computed from: 2. Spearman’s r is Pearson’s r computed from the ranks.

3. Spearman’s r is less sensitive to extreme observations. (outliers) 4. The value of Pearson’s r is much more sensitive to extreme outliers. This is similar to the comparison between the median and the mean, the standard deviation and the pseudo-standard deviation. The mean and standard deviation are more sensitive to outliers than the median and pseudo- standard deviation.

Scatter plots

Some Scatter Patterns


Non-Linear Patterns

Measuring correlation 1. Pearson’s correlation coefficient r 2. Spearman’s rank correlation coefficient r

Simple Linear Regression Fitting straight lines to data

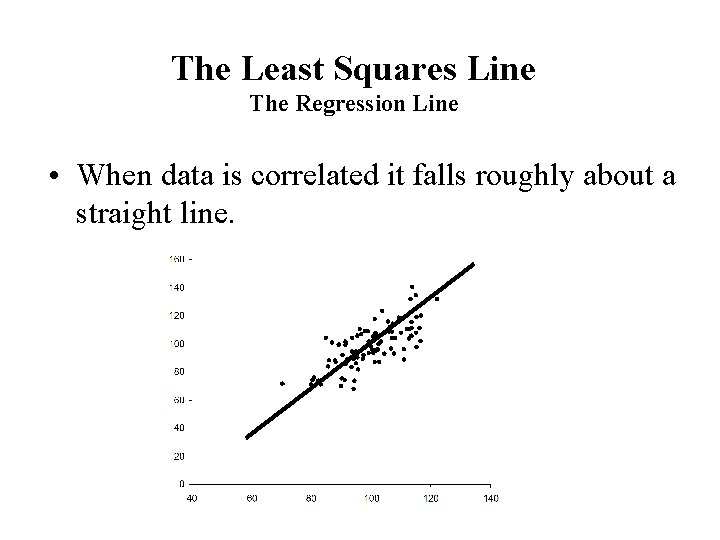
The Least Squares Line The Regression Line • When data is correlated it falls roughly about a straight line.

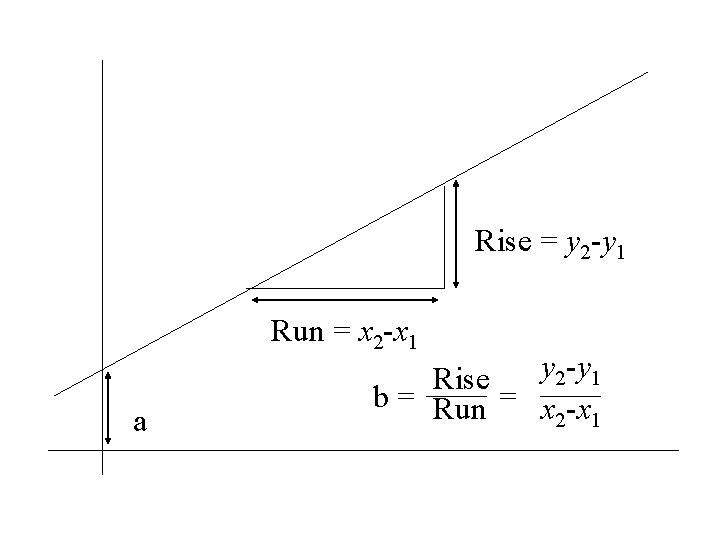
In this situation wants to: • Find the equation of the straight line through the data that yields the best fit. The equation of any straight line: is of the form: Y = a + b. X b = the slope of the line a = the intercept of the line

Rise = y 2 -y 1 Run = x 2 -x 1 a y 2 -y 1 Rise b = Run = x -x 2 1

• a is the value of Y when X is zero • b is the rate that Y increases per unit increase in X. • For a straight line this rate is constant. • For non linear curves the rate that Y increases per unit increase in X varies with X.

Linear

Non-linear

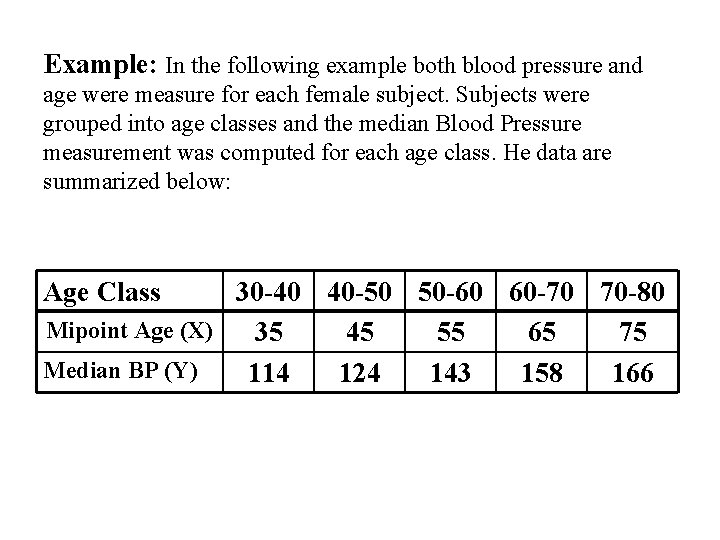
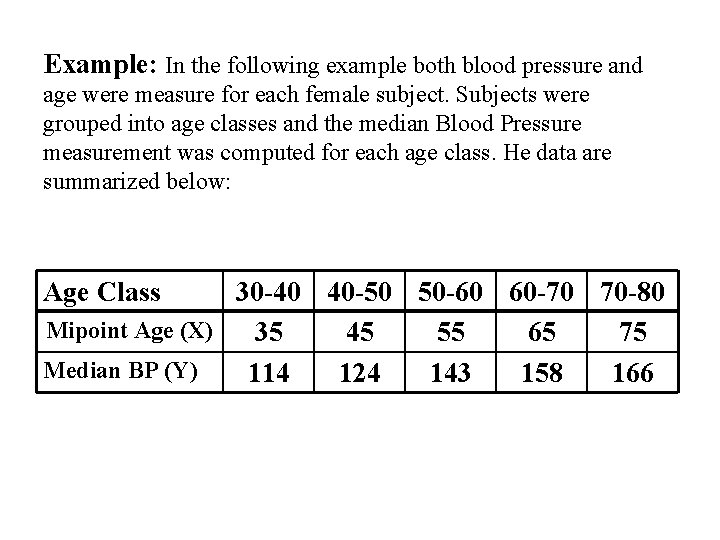
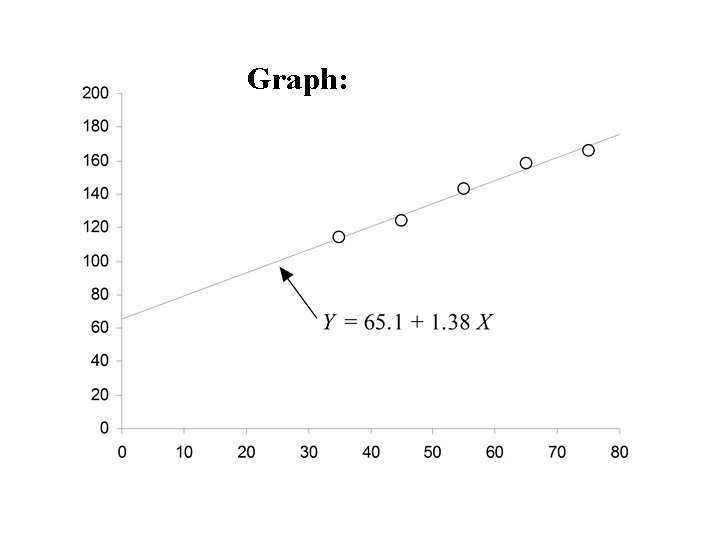
Example: In the following example both blood pressure and age were measure for each female subject. Subjects were grouped into age classes and the median Blood Pressure measurement was computed for each age class. He data are summarized below: Age Class 30 -40 40 -50 50 -60 60 -70 70 -80 Mipoint Age (X) 35 45 55 65 75 Median BP (Y) 114 124 143 158 166

Graph:

Interpretation of the slope and intercept 1. Intercept – value of Y at X = 0. – Predicted Blood pressure of a newborn (65. 1). – This interpretation remains valid only if linearity is true down to X = 0. 2. Slope – rate of increase in Y per unit increase in X. – Blood Pressure increases 1. 38 units each year.

The Least Squares Line Fitting the best straight line to “linear” data

Reasons for fitting a straight line to data 1. It provides a precise description of the relationship between Y and X. 2. The interpretation of the parameters of the line (slope and intercept) leads to an improved understanding of the phenomena that is under study. 3. The equation of the line is useful for prediction of the dependent variable (Y) from the independent variable (X).

Assume that we have collected data on two variables X and Y. Let (x 1, y 1) (x 2, y 2) (x 3, y 3) … (xn, yn) denote the pairs of measurements on the on two variables X and Y for n cases in a sample (or population)

Let Y=a +b. X denote an arbitrary equation of a straight line. a and b are known values. This equation can be used to predict for each value of X, the value of Y. For example, if X = xi (as for the ith case) then the predicted value of Y is:

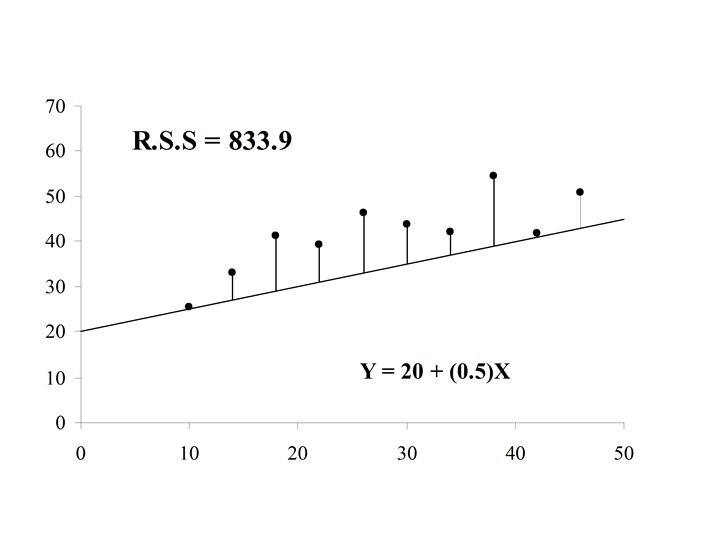
For example if Y = a + b X = 25. 2 + 2. 0 X Is the equation of the straight line. and if X = xi = 20 (for the ith case) then the predicted value of Y is:

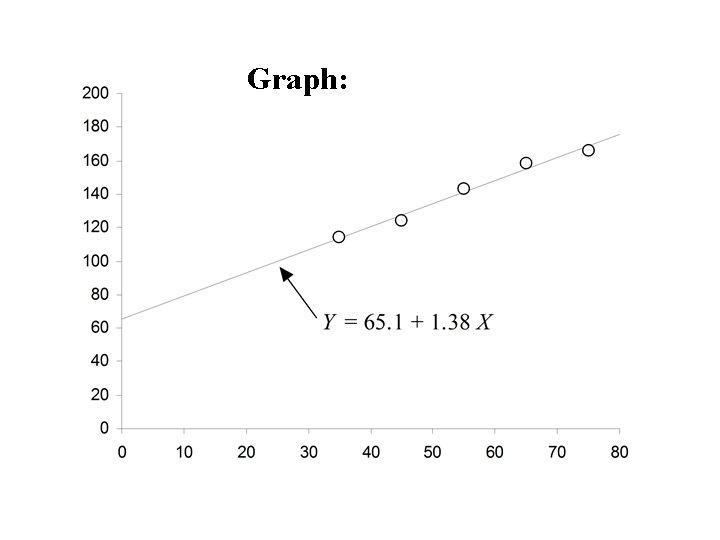
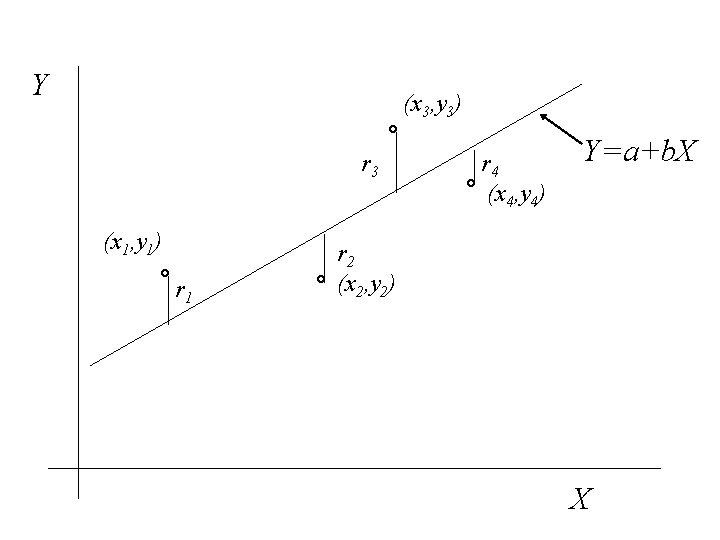
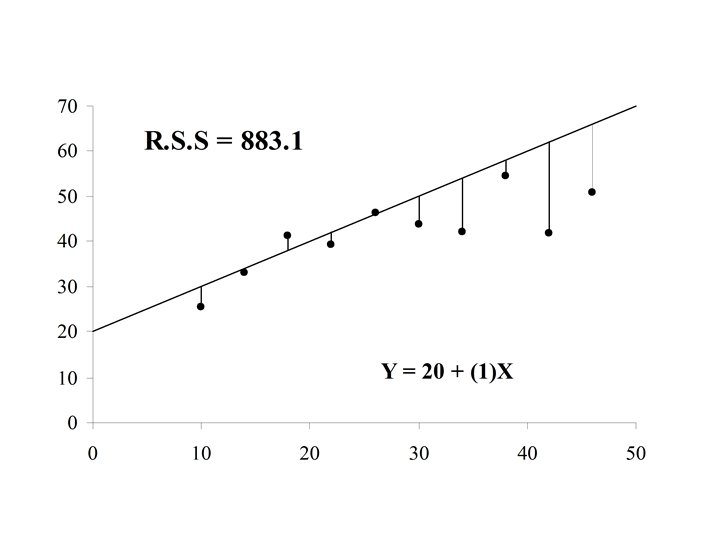
If the actual value of Y is yi = 70. 0 for case i, then the difference is the error in the prediction for case i. is also called the residual for case i

If the residual can be computed for each case in the sample, The residual sum of squares (RSS) is a measure of the “goodness of fit of the line Y = a + b. X to the data

Y (x 3, y 3) r 3 (x 1, y 1) r 1 r 4 (x 4, y 4) Y=a+b. X r 2 (x 2, y 2) X

The optimal choice of a and b will result in the residual sum of squares attaining a minimum. If this is the case than the line: Y = a + b. X is called the Least Squares Line







The equation for the least squares line Let

Computing Formulae:
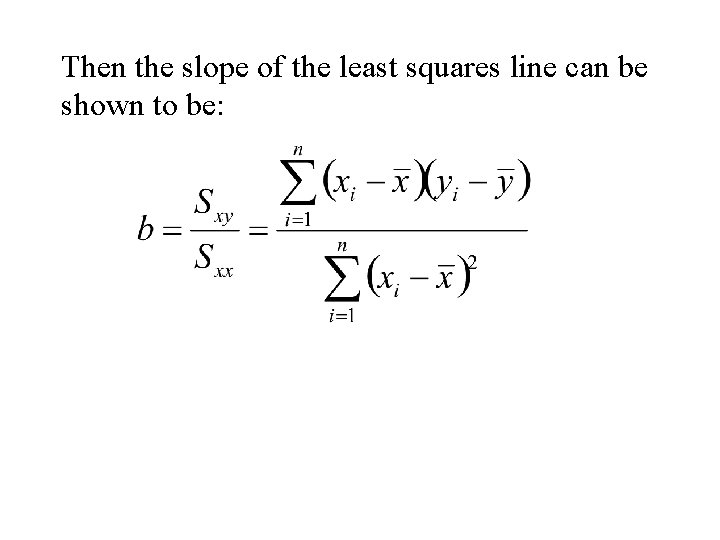
Then the slope of the least squares line can be shown to be:

and the intercept of the least squares line can be shown to be:
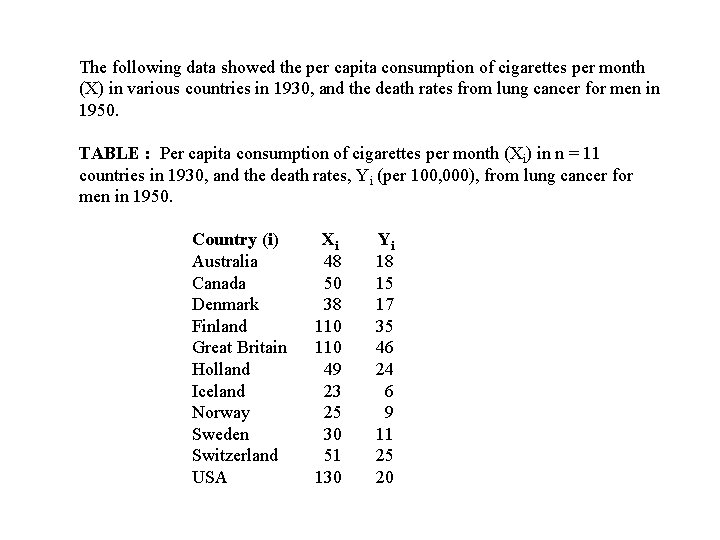
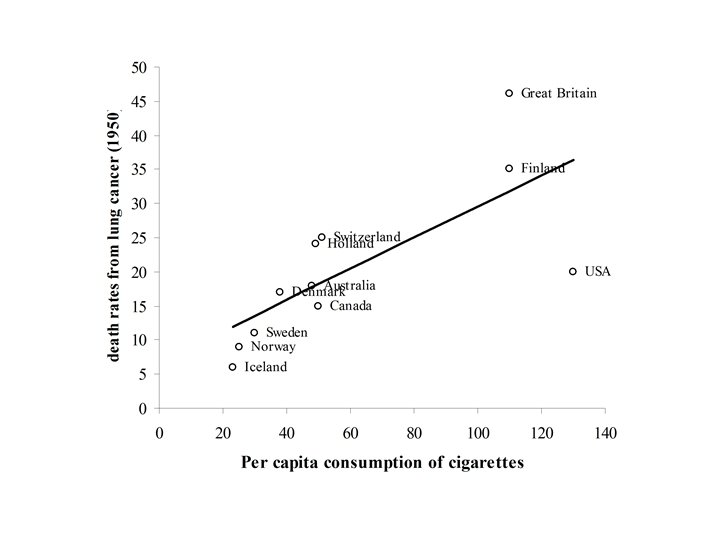
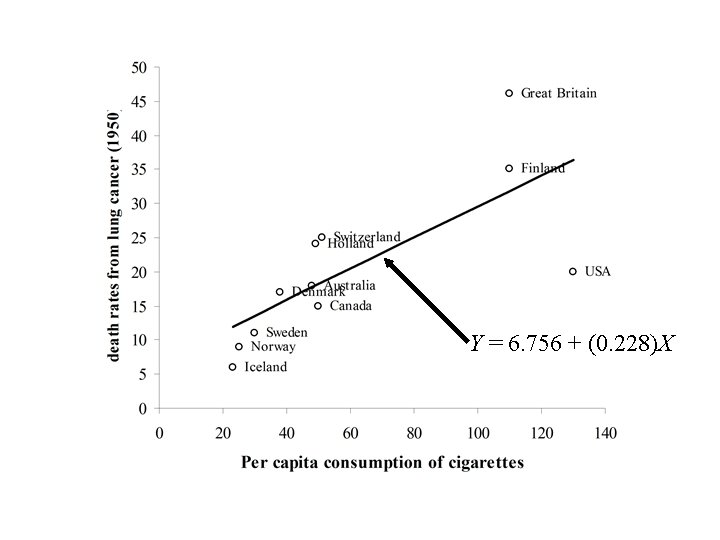
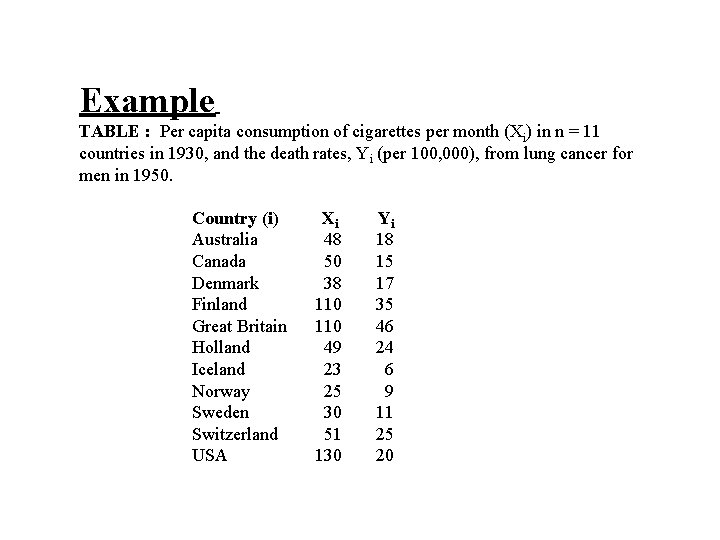
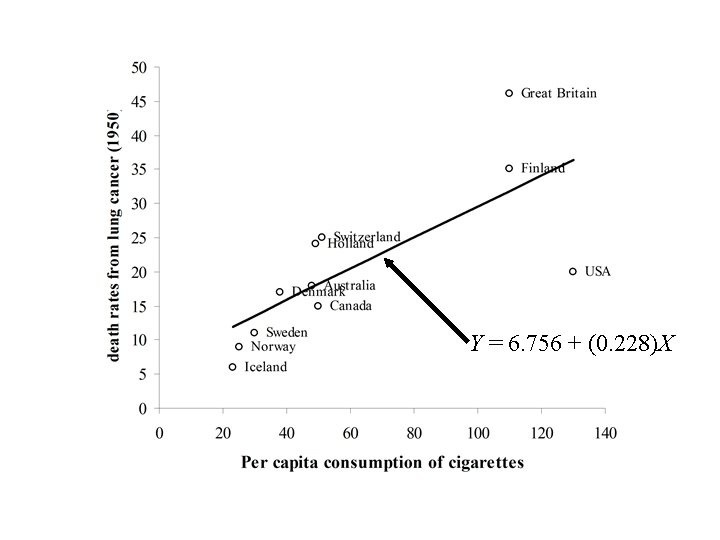
The following data showed the per capita consumption of cigarettes per month (X) in various countries in 1930, and the death rates from lung cancer for men in 1950. TABLE : Per capita consumption of cigarettes per month (Xi) in n = 11 countries in 1930, and the death rates, Yi (per 100, 000), from lung cancer for men in 1950. Country (i) Xi Yi Australia 48 18 Canada 50 15 Denmark 38 17 Finland 110 35 Great Britain 110 46 Holland 49 24 Iceland 23 6 Norway 25 9 Sweden 30 11 Switzerland 51 25 USA 130 20



Fitting the Least Squares Line

Fitting the Least Squares Line First compute the following three quantities:

Computing Estimate of Slope and Intercept

Y = 6. 756 + (0. 228)X

Interpretation of the slope and intercept 1. Intercept – value of Y at X = 0. – Predicted death rate from lung cancer (6. 756) for men in 1950 in Counties with no smoking in 1930 (X = 0). 2. Slope – rate of increase in Y per unit increase in X. – Death rate from lung cancer for men in 1950 increases 0. 228 units for each increase of 1 cigarette per capita consumption in 1930.

Example: In the following example both blood pressure and age were measure for each female subject. Subjects were grouped into age classes and the median Blood Pressure measurement was computed for each age class. He data are summarized below: Age Class 30 -40 40 -50 50 -60 60 -70 70 -80 Mipoint Age (X) 35 45 55 65 75 Median BP (Y) 114 124 143 158 166

Fitting the Least Squares Line

Fitting the Least Squares Line First compute the following three quantities:

Computing Estimate of Slope and Intercept

Graph:

Relationship between correlation and Linear Regression 1. Pearsons correlation. • Takes values between – 1 and +1

2. Least squares Line Y = a + b. X – Minimises the Residual Sum of Squares: – The Sum of Squares that measures the variability in Y that is unexplained by X. – This can also be denoted by: SSunexplained

Some other Sum of Squares: – The Sum of Squares that measures the total variability in Y (ignoring X).

– The Sum of Squares that measures the total variability in Y that is explained by X.

It can be shown: (Total variability in Y) = (variability in Y explained by X) + (variability in Y unexplained by X)

It can also be shown: = proportion variability in Y explained by X. = the coefficient of determination

Further: = proportion variability in Y that is unexplained by X.

Example TABLE : Per capita consumption of cigarettes per month (Xi) in n = 11 countries in 1930, and the death rates, Yi (per 100, 000), from lung cancer for men in 1950. Country (i) Xi Yi Australia 48 18 Canada 50 15 Denmark 38 17 Finland 110 35 Great Britain 110 46 Holland 49 24 Iceland 23 6 Norway 25 9 Sweden 30 11 Switzerland 51 25 USA 130 20

Fitting the Least Squares Line First compute the following three quantities:

Computing Estimate of Slope and Intercept
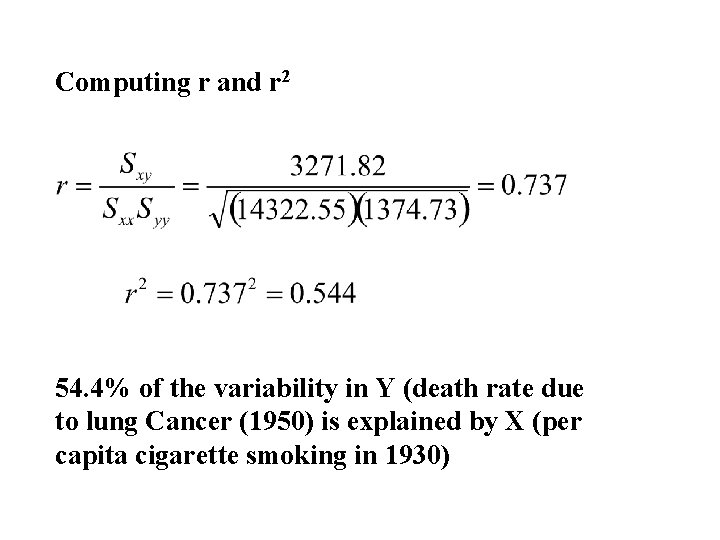
Computing r and r 2 54. 4% of the variability in Y (death rate due to lung Cancer (1950) is explained by X (per capita cigarette smoking in 1930)

Y = 6. 756 + (0. 228)X

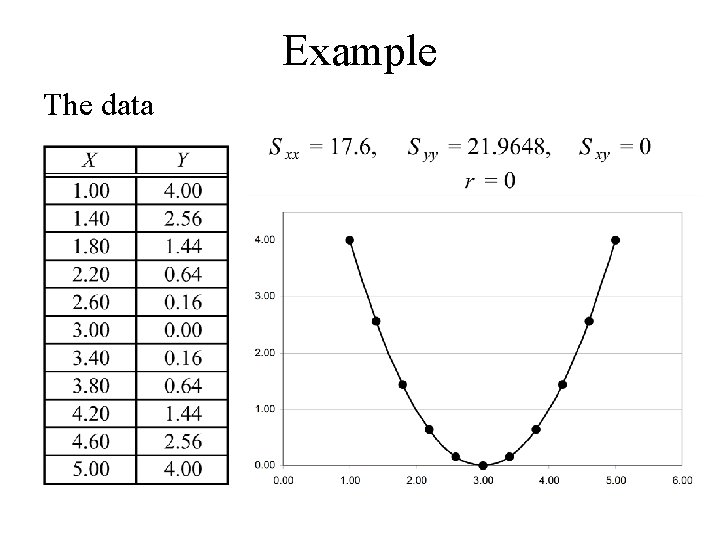
Comments • Correlation will be +1 or -1 if the data lies on a straight line. • Correlation can be zero or close to zero if the data is either – Not related or – In some situations non-linear

Example The data

One should be careful in interpreting zero correlation. It does not necessarily imply that Y is not related to X. It could happen that Y is non-linearly related to X. One should plot Y vs X before concluding that Y is not related to X.
 Multivariate descriptive statistics
Multivariate descriptive statistics What is the lower quartile measure of this box plot?
What is the lower quartile measure of this box plot? What are descriptive techniques
What are descriptive techniques Jack the box
Jack the box Graphical descriptive techniques
Graphical descriptive techniques Graphical descriptive techniques
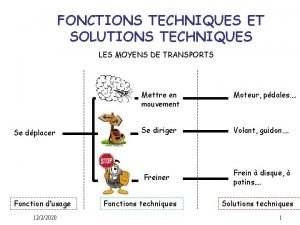
Graphical descriptive techniques Fonction technique scooter
Fonction technique scooter Formuö
Formuö Novell typiska drag
Novell typiska drag Nationell inriktning för artificiell intelligens
Nationell inriktning för artificiell intelligens Ekologiskt fotavtryck
Ekologiskt fotavtryck Varför kallas perioden 1918-1939 för mellankrigstiden?
Varför kallas perioden 1918-1939 för mellankrigstiden? En lathund för arbete med kontinuitetshantering
En lathund för arbete med kontinuitetshantering Underlag för särskild löneskatt på pensionskostnader
Underlag för särskild löneskatt på pensionskostnader Tidböcker
Tidböcker Anatomi organ reproduksi
Anatomi organ reproduksi Densitet vatten
Densitet vatten Datorkunskap för nybörjare
Datorkunskap för nybörjare Boverket ka
Boverket ka Att skriva debattartikel
Att skriva debattartikel Delegerande ledarskap
Delegerande ledarskap Nyckelkompetenser för livslångt lärande
Nyckelkompetenser för livslångt lärande Påbyggnader för flakfordon
Påbyggnader för flakfordon Vätsketryck formel
Vätsketryck formel Offentlig förvaltning
Offentlig förvaltning Urban torhamn
Urban torhamn Presentera för publik crossboss
Presentera för publik crossboss Vad är ett minoritetsspråk
Vad är ett minoritetsspråk Bat mitza
Bat mitza Treserva lathund
Treserva lathund Fimbrietratt
Fimbrietratt Claes martinsson
Claes martinsson Centrum för kunskap och säkerhet
Centrum för kunskap och säkerhet Verifikationsplan
Verifikationsplan Bra mat för unga idrottare
Bra mat för unga idrottare Verktyg för automatisering av utbetalningar
Verktyg för automatisering av utbetalningar Rutin för avvikelsehantering
Rutin för avvikelsehantering Smärtskolan kunskap för livet
Smärtskolan kunskap för livet Ministerstyre för och nackdelar
Ministerstyre för och nackdelar Tack för att ni har lyssnat
Tack för att ni har lyssnat Referatmarkering
Referatmarkering Redogör för vad psykologi är
Redogör för vad psykologi är Stål för stötfångarsystem
Stål för stötfångarsystem Atmosfr
Atmosfr Borra hål för knoppar
Borra hål för knoppar Vilken grundregel finns det för tronföljden i sverige?
Vilken grundregel finns det för tronföljden i sverige? Formel standardavvikelse
Formel standardavvikelse Tack för att ni har lyssnat
Tack för att ni har lyssnat Rita perspektiv
Rita perspektiv Verksamhetsanalys exempel
Verksamhetsanalys exempel Tobinskatten för och nackdelar
Tobinskatten för och nackdelar Toppslätskivling dos
Toppslätskivling dos Gibbs reflekterande cykel
Gibbs reflekterande cykel Egg för emanuel
Egg för emanuel Elektronik för barn
Elektronik för barn Fredsgudinnan
Fredsgudinnan Strategi för svensk viltförvaltning
Strategi för svensk viltförvaltning Var 1721 för stormaktssverige
Var 1721 för stormaktssverige Ellika andolf
Ellika andolf Ro i rom pax
Ro i rom pax Tack för att ni lyssnade
Tack för att ni lyssnade Uppställning multiplikation
Uppställning multiplikation Bunden till c-dur
Bunden till c-dur Inköpsprocessen steg för steg
Inköpsprocessen steg för steg Rådet för byggkompetens
Rådet för byggkompetens Ledarskapsteorier
Ledarskapsteorier Vad är hsil
Vad är hsil Myndigheten för delaktighet
Myndigheten för delaktighet Frgar
Frgar Tillitsbaserad ledning
Tillitsbaserad ledning Läkarutlåtande för livränta
Läkarutlåtande för livränta Vad är en punkthöjd
Vad är en punkthöjd Geometriska former i förskolan
Geometriska former i förskolan Vishnuismen
Vishnuismen Mitos steg
Mitos steg Bris för vuxna
Bris för vuxna Big brother rösta
Big brother rösta Logistische funktion ableitung
Logistische funktion ableitung Multivariate binomial distribution
Multivariate binomial distribution Multivariate pdf
Multivariate pdf What is multivariate analysis?
What is multivariate analysis? Multivariate regression spss
Multivariate regression spss Log likelihood of multivariate normal distribution
Log likelihood of multivariate normal distribution Maximum a posteriori estimation for multivariate gaussian
Maximum a posteriori estimation for multivariate gaussian Multivariate pdf
Multivariate pdf Difference between correlation and regression
Difference between correlation and regression Multivariate analysis of variance example
Multivariate analysis of variance example Manova with repeated measures
Manova with repeated measures Ratio test
Ratio test Multivariate methods in machine learning
Multivariate methods in machine learning Nature of multivariate analysis
Nature of multivariate analysis Multivariate verfahren psychologie
Multivariate verfahren psychologie Multivariate analysis of variance and covariance
Multivariate analysis of variance and covariance Univariate vs multivariate
Univariate vs multivariate Multivariate scatter plot
Multivariate scatter plot Advanced and multivariate statistical methods
Advanced and multivariate statistical methods Multivariate analysis
Multivariate analysis Multivariate statistics for the environmental sciences
Multivariate statistics for the environmental sciences Multivariate statistical analysis
Multivariate statistical analysis Multivariate analysis
Multivariate analysis Multivariate histogram
Multivariate histogram Multivariate analysis
Multivariate analysis Multivariate pattern analysis
Multivariate pattern analysis Example of descriptive data mining
Example of descriptive data mining Complex data types in data mining
Complex data types in data mining Summarizing qualitative data in excel
Summarizing qualitative data in excel Spatial data input
Spatial data input Data modeling techniques
Data modeling techniques Data mining concepts and techniques
Data mining concepts and techniques Data mining concepts and techniques
Data mining concepts and techniques Sp_cdc_scan
Sp_cdc_scan Data modelling techniques in business intelligence
Data modelling techniques in business intelligence Data consolidation techniques
Data consolidation techniques What is data
What is data Data mining slides
Data mining slides Data mining concepts and techniques slides
Data mining concepts and techniques slides Data management techniques
Data management techniques Data capture methods
Data capture methods Data quality control techniques
Data quality control techniques Binning techniques in data mining
Binning techniques in data mining Digital encoding schemes
Digital encoding schemes Data recovery techniques
Data recovery techniques Association data mining techniques
Association data mining techniques Classification alternative techniques in data mining
Classification alternative techniques in data mining Projective techniques of data collection
Projective techniques of data collection Digital data communication techniques
Digital data communication techniques Data presentation techniques
Data presentation techniques Data encoding techniques
Data encoding techniques Advanced data visualization techniques
Advanced data visualization techniques Descriptive research question
Descriptive research question Example of descriptive paragraph
Example of descriptive paragraph Descriptive headings
Descriptive headings What instrumentation do you hear in this work?
What instrumentation do you hear in this work? Advantages of descriptive research
Advantages of descriptive research Descriptive statistics in business
Descriptive statistics in business Question lead journalism
Question lead journalism What is descriptive equivalent
What is descriptive equivalent Transition words for descriptive essay
Transition words for descriptive essay Why aren t descriptive investigations repeatable
Why aren t descriptive investigations repeatable Predictive function of marketing research
Predictive function of marketing research Aim of descriptive writing
Aim of descriptive writing Descriptive and normative
Descriptive and normative Genitive case
Genitive case Descriptive ethics
Descriptive ethics Paradigm vs model
Paradigm vs model Narrative essay about a famous person
Narrative essay about a famous person Descriptive norm
Descriptive norm Descriptive essay beach using five senses
Descriptive essay beach using five senses Hyponymy
Hyponymy Concept construct and variable in research
Concept construct and variable in research Limitations of cross sectional study
Limitations of cross sectional study Descriptive research question
Descriptive research question Research design descriptive quantitative
Research design descriptive quantitative Descriptive research design
Descriptive research design Solomon four group design
Solomon four group design Realism vs anti realism
Realism vs anti realism Correlational descriptive design
Correlational descriptive design Your, fam.) esposo es italiano.
Your, fam.) esposo es italiano. Descriptive and possessive adjectives
Descriptive and possessive adjectives Imagery olfactory
Imagery olfactory Individuals: an essay in descriptive metaphysics
Individuals: an essay in descriptive metaphysics What event happened first my shopping norte's nightmare
What event happened first my shopping norte's nightmare Patterns of paragraph development examples
Patterns of paragraph development examples Exploratory research vs conclusive research
Exploratory research vs conclusive research Chapter 1 of mice and men
Chapter 1 of mice and men Impressionistic descriptive writing
Impressionistic descriptive writing Numerical descriptive measures exercises
Numerical descriptive measures exercises Descriptive essay notes
Descriptive essay notes