Multivalued Dependencies and Fourth Normal Form COSC 6340

Multi-valued Dependencies and Fourth Normal Form COSC 6340 Ch. Eick: 4 th. NF and MVD's

Topics Covered 1. 2. 3. Definition of Multivalued Dependencies Reasoning about MVDs Fourth Normal Form Ch. Eick: 4 th. NF and MVD's 2

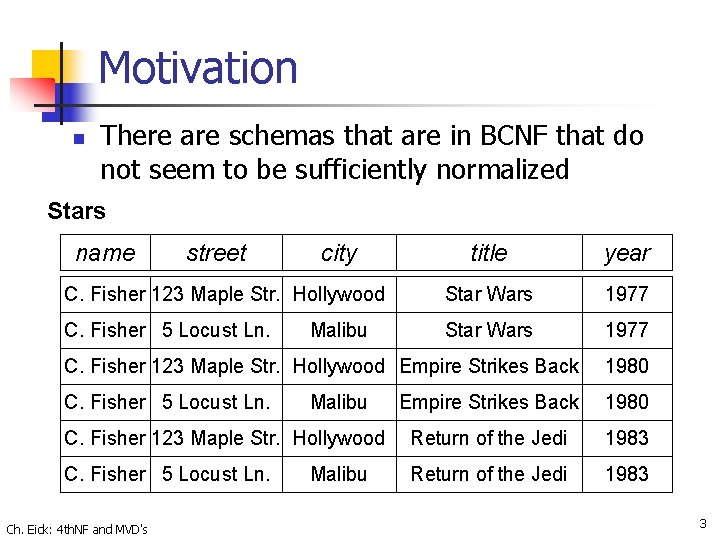
Motivation n There are schemas that are in BCNF that do not seem to be sufficiently normalized Stars name street city title year C. Fisher 123 Maple Str. Hollywood Star Wars 1977 C. Fisher 5 Locust Ln. Star Wars 1977 Malibu C. Fisher 123 Maple Str. Hollywood Empire Strikes Back 1980 C. Fisher 5 Locust Ln. Empire Strikes Back 1980 C. Fisher 123 Maple Str. Hollywood Return of the Jedi 1983 C. Fisher 5 Locust Ln. Return of the Jedi 1983 Ch. Eick: 4 th. NF and MVD's Malibu 3

Attribute Independence n n n No reason to associate address with one movie and not another When we repeat address and movie facts in all combinations, there is obvious redundancy However, NO BCNF violation in Stars relation n n There are no non-trivial FD’s at all, all five attributes form the only superkey Why? Ch. Eick: 4 th. NF and MVD's 4

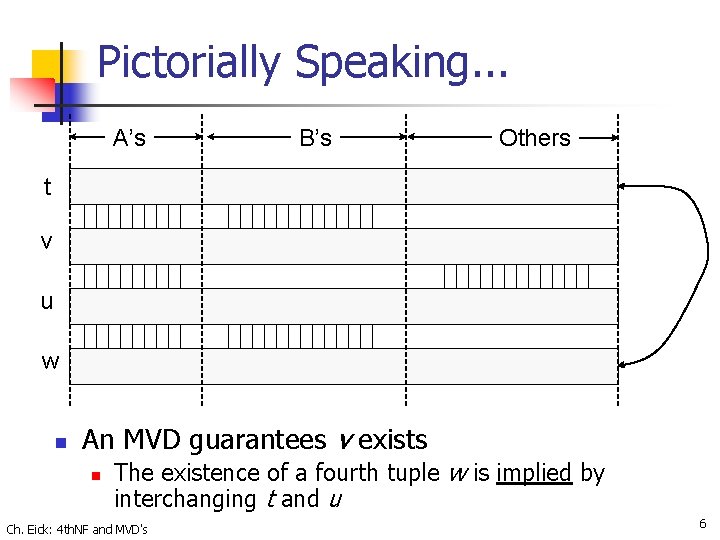
Multi-valued Dependency Definition: Multivalued dependency (MVD): A 1 A 2…An B 1 B 2…Bm holds for relation R if: For all tuples t, u in R If t[A 1 A 2. . . An] = u[A 1 A 2. . . An], then there exists a v in R such that: (1) v[A 1 A 2. . . An] = t[A 1 A 2. . . An] = u[A 1 A 2. . . An] (2) v[B 1 B 2…Bm] = t[B 1 B 2…Bm] (3) v[C 1 C 2…Ck] = u[C 1 C 2…Ck], where C 1 C 2…Ck is all attributes in R except (A 1 A 2. . . An B 1 B 2…Bm) Ch. Eick: 4 th. NF and MVD's 5

Pictorially Speaking. . . A’s B’s Others t v u w n An MVD guarantees v exists n The existence of a fourth tuple w is implied by interchanging t and u Ch. Eick: 4 th. NF and MVD's 6

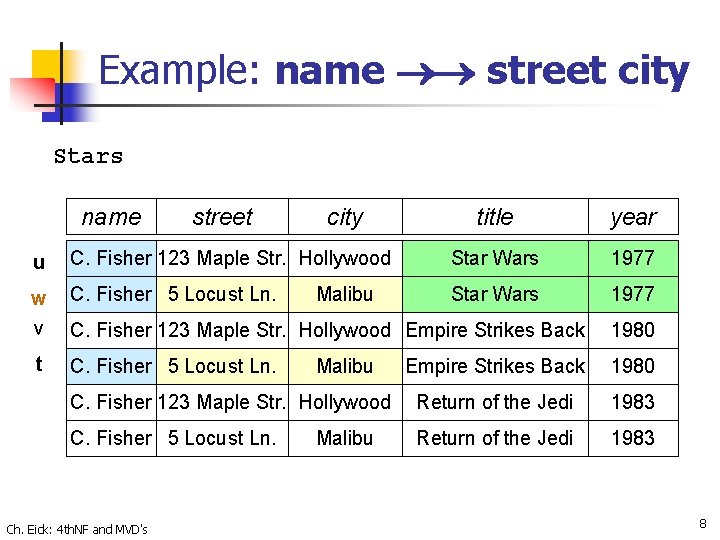
Example: name street city Stars name t street city title year C. Fisher 123 Maple Str. Hollywood Star Wars 1977 C. Fisher 5 Locust Ln. Star Wars 1977 Malibu v C. Fisher 123 Maple Str. Hollywood Empire Strikes Back 1980 u C. Fisher 5 Locust Ln. Empire Strikes Back 1980 C. Fisher 123 Maple Str. Hollywood Return of the Jedi 1983 C. Fisher 5 Locust Ln. Return of the Jedi 1983 Ch. Eick: 4 th. NF and MVD's Malibu 7

Example: name street city Stars name street city title year u C. Fisher 123 Maple Str. Hollywood Star Wars 1977 w v C. Fisher 5 Locust Ln. Star Wars 1977 C. Fisher 123 Maple Str. Hollywood Empire Strikes Back 1980 t C. Fisher 5 Locust Ln. Empire Strikes Back 1980 C. Fisher 123 Maple Str. Hollywood Return of the Jedi 1983 C. Fisher 5 Locust Ln. Return of the Jedi 1983 Ch. Eick: 4 th. NF and MVD's Malibu 8

More on MVDs n Intuitively, A 1 A 2…An B 1 B 2…Bm says that the relationship between A 1 A 2…An and B 1 B 2…Bm is independent of the relationship between A 1 A 2…An and R {B 1 B 2…Bm} n n Functional dependencies rule out certain tuples from being in a relation n n MVD's uncover situations where independent facts related to a certain object are being squished together in one relation How? Multivalued dependencies require that other tuples of a certain form be present in the relation n a. k. a. tuple-generating dependencies Ch. Eick: 4 th. NF and MVD's 9

Let’s Illustrate n In Stars, we must repeat the movie (title, year) once for each address (street, city) a movie star has n n Alternatively, we must repeat the address for each movie a star has made Example: Stars with name street city name street city C. Fisher 123 Maple Str. Hollywood C. Fisher 5 Locust Ln. Malibu C. Fisher 123 Maple Str. Hollywood n title year Star Wars 1977 Empire Strikes Back 1980 Return of the Jedi 1983 Is an incomplete extent of Stars n Infer the existence of a fourth tuple under the given MVD Ch. Eick: 4 th. NF and MVD's 10

Trivial MVDs n Trivial MVD A 1 A 2…An B 1 B 2…Bm where B 1 B 2…Bm is a subset of A 1 A 2…An or (A 1 A 2…An B 1 B 2…Bm ) contains all attributes of R Ch. Eick: 4 th. NF and MVD's 11

Reasoning About MVDs n FD-IS-AN-MVD Rule (Replication) If A 1 A 2…An B 1 B 2…Bm then A 1 A 2…An B 1 B 2…Bm holds Ch. Eick: 4 th. NF and MVD's 12

Reasoning About MVDs n COMPLEMENTATION Rule If A 1 A 2…An B 1 B 2…Bm then A 1 A 2…An C 1 C 2…Ck where C 1 C 2…Ck is all attributes in R except (A 1 A 2…An B 1 B 2…Bm ) n AUGMENTATION Rule If X Y and W Z then WX YZ n TRANSITIVITY Rule If X Y and Y Z then X (Z-Y) Ch. Eick: 4 th. NF and MVD's 13

Coalescence Rule for MVD X Y If: W: W Z Then: X Z Remark: Y and W have to be disjoint and Z has to be a subset of or equal to Y Ch. Eick: 4 th. NF and MVD's 14

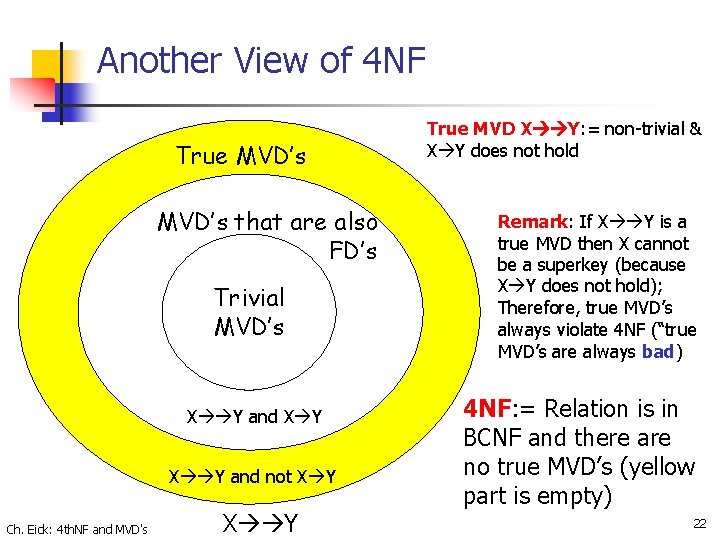
Definition 4 NF n n Given: relation R and set of MVD's for R Definition: R is in 4 NF with respect to its MVD's if for every non-trivial MVD A 1 A 2…An B 1 B 2…Bm , A 1 A 2…An is a superkey Note: Since every FD is also an MVD, 4 NF implies BCNF Example: Stars is not in 4 NF Ch. Eick: 4 th. NF and MVD's 15

Decomposition Algorithm (1) apply closure to the user-specified FD's and MVD's**: (2) repeat until no more 4 NF violations: if R with AA ->> BB violates 4 NF then: (2 a) decompose R into R 1(AA, BB) and R 2(AA, CC), where CC is all attributes in R except (AA BB) (2 b) assign FD's and MVD's to the new relations** n ** MVD's: hard problem! No simple test analogous to computing the attribute closure for FD’s exists for MVD’s. You are stuck to have to use the 5 inference rules for MVD’s when computing the closure! Ch. Eick: 4 th. NF and MVD's 16

Exercise n n Decompose Stars into a set of relations that are in 4 NF. name street city is a 4 NF violation Apply decomposition: R(name, street, city) S(name, title, year) What about name street city in R and name title year in S? Ch. Eick: 4 th. NF and MVD's 17

Exercise For the relation R(A, B, C, D) with only MVD’s A B and A C find all 4 NF violations and decompose R into a collection of relation schemas in 4 NF. Ch. Eick: 4 th. NF and MVD's 18

Solution n n Since there are no functional dependencies, the only key is all four attributes, ABCD. Thus, each of the nontrivial multivalued dependencies A->->B and A->->C violate 4 NF. Separate out the attributes of these dependencies, first decomposing into AB and ACD Then decompose the latter into AC and AD because A->->C is still a 4 NF violation for ACD. The final set of relations are AB, AC, and AD. Ch. Eick: 4 th. NF and MVD's 19

Exercise Suppose we have relation R(A, B, C) with MVD A B. If we know that the tuples (a, b 1, c 1), (a, b 2, c 2), and (a, b 3, c 3) are in the current instance of R, what other tuples do we know must also be in R? Ch. Eick: 4 th. NF and MVD's 20

Solution n n Since A->->B, and all the tuples have the same value for attribute A, we can pair the B-value from any tuple with the value of the remaining attribute C from any other tuple. Thus, we know that R must have at least the nine tuples of the form (a, b, c), where b is any of b 1, b 2, or b 3, and c is any of c 1, c 2, or c 3. That is, we can derive, using the definition of a multivalued dependency, that each of the tuples (a, b 1, c 2), (a, b 1, c 3), (a, b 2, c 1), (a, b 2, c 3), (a, b 3, c 1), and (a, b 3, c 2) are also in R. Ch. Eick: 4 th. NF and MVD's 21

Another View of 4 NF True MVD’s that are also FD’s Trivial ‘s MVD’s X Y and not X Y Ch. Eick: 4 th. NF and MVD's X Y True MVD X Y: = non-trivial & X Y does not hold Remark: If X Y is a true MVD then X cannot be a superkey (because X Y does not hold); Therefore, true MVD’s always violate 4 NF (“true MVD’s are always bad) 4 NF: = Relation is in BCNF and there are no true MVD’s (yellow part is empty) 22

H 1 -2005 -Problem 8 8) Normalization [6] graded R(A, B, C, D, E, F) is given with: (1) AB CD (2)CD AB (3)AB F (4) F E a) What are the candidate keys of relation R? [1] b) b) Transform R into a relational schema that is in BCNF and does not have any lost functional dependencies! [5] Correct Solution: a) Candidate keys: AB and CD b) Decompose R into R 1(A, B, C, D, F) with local FD’s (1), (2), (3) and R 2(E, F) with local FD’s (4) Due to the fact that all four dependencies are still present no functional dependency has been lost. Moreover, all functional depencies are good A non-optimal (“too many relations”) solution I also saw was: Decompose R into R 1(A, B, C, D) with local functional dependencies AB CD and CD AB, R 2(A, B, F) with local functional dependencies AB F and R 3(F, E) with local functional dependencies F A. . Ch. Eick: 4 th. NF and MVD's 23

Problem 1; H 1 -2004 a. b. c. Candidate keys are: {a, b}, {a, d}, {a, e} 14 superkeys total All but the first functional dependency are bad Ch. Eick: 4 th. NF and MVD's 24

Problem 2; H 2 -04 a. b. c. d. e. f. No; E BC is a “true” multi-valued dependency and E is not a candidate key (as a matter of fact {E}+={A, D, E, F} see below) No (but just mentioning neither E ABC nor E CF holds is not sufficient (e. g. if E ABC holds then the decomposition is lossless!) ) --- a counter examples should be given to show that the statement is false! Yes C is candidate key; therefore C BDEF Yes E BC and BC BCD implies E D due to MVDtransitivity (C CD BC BCD) Yes E BC; therefore E ADF; moreover, C ADF and using the Coalescence Rule we obtain E ADF; therefore, E A holds No R is not in BCNF because E ADF holds and E is not a candidate key. Ch. Eick: 4 th. NF and MVD's 25

Problem 3 a-2004 From A B and A C we can infer: A BC? ? (1) A C A AC (2) A B AC ABC (3) AC ABC AC DE (4) A AC, AC DE A DE Wrong!! (5) A DE A BC Using: 1. Augmentation, 2. Augmentation, 3. Complementation, 4. Transitivity, 5. Complementation Remark: This problem will be revised in Homework 3 -2005; it is too complicated to worry about it for the midterm exam! Ch. Eick: 4 th. NF and MVD's 26

MDV’s and FD’s --- Ungraded Homework Assume we have a relation R(A, B, C, D, E) with the following dependencies: (1) AB CDE (2) CD ABE (3) E DB Answer the following questions giving reasons for your answers: a) Is R in BCNF? ? ? (answer after Spring break) Warning: The presence of the MVD might imply other functional dependencies (see textbook page 637) b) Does ABE D hold for R? yes c) Does CD B hold for R? yes d) Does E D always hold for R (either show that this dependency can be inferred from the given 3 dependencies, or give a counter example of a relation that satisfies (1), (2), (3) but violates E D)? No Ch. Eick: 4 th. NF and MVD's 27