Multiscale Simulation Methods Russel Caflisch Math Materials Science

Multiscale Simulation Methods Russel Caflisch Math & Materials Science Depts, UCLA IPAM, Sept 13, 2005

Outline • Simulations – Equations often unavailable or cumbersome – New multiscale strategies needed • Perron-Cluster Analysis – Automatically identifies metastable states – Example of clustering algorithm • Equation-Free Multiscale Method of Kevrekidis – Using simulation results to form approximate model on fine scale – Extend to coarse scale • Interpolated fluid/Monte Carlo method for rarefied gas dynamics – Combine particle and continuum descriptions of gas in single hybrid method • Conclusions IPAM, Sept 13, 2005

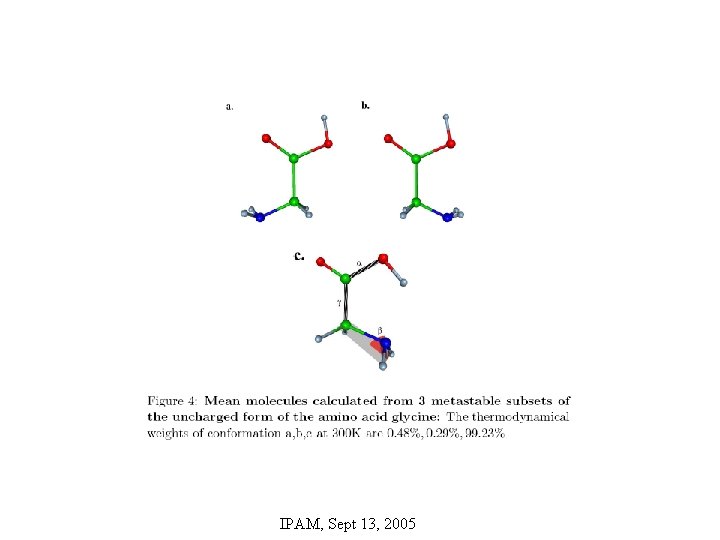
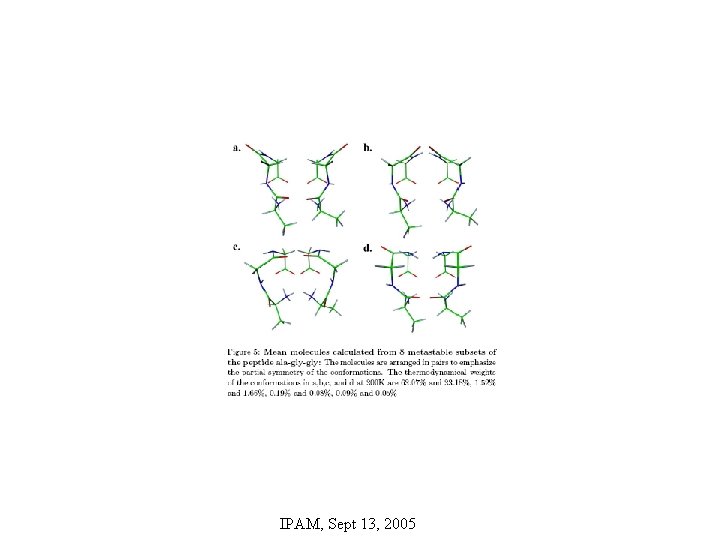
Perron-Cluster Analysis (PCCA) • Objective: Identify modes for reduced order description of a complex system – E. g. metastable states for bio molecule • Method: clustering methods – Principal component analysis (PCA) • Principal orthogonal decomposition (POD) – Independent component analysis (ICA) – PCCA • Nonlinear method • Similar to Laplace projection IPAM, Sept 13, 2005

Perron Vectors • Stochastic matrix T – Nonegative entries – Rows sum to 1 – Assume eigenvalue 1 has multiplicity k • Invariant sets – Invariant set of dimension di – Invariant measure -> eigenvector Xi with eigenvalue 1 – Matrix X=(X 1 , …, Xk ) • Characteristic “functions” – Let χi with χ=(0, …, 0, 1, … 1, 0, … 0)t with di 1’s – For χi ∙ χj =0 for different i, j – Matrix of e-vectors χ=(χ1 , …, χk ) • Coordinate transformation A – χ=XA IPAM, Sept 13, 2005

PCCA • Stochastic matrix T – Nonegative entries – Rows sum to 1 – Assume k eigenvalues close to 1 • Nearly-invariant measures – eigenvector Xi with eigenvalue near 1 – Matrix X=(X 1 , …, Xk ) • Find – transformation matrix A, – characteristic matrix χ – χ ≈ XA • Robust algorithm for finding A, χ – Deuflhard, Dellnitz, Junge & Schutte (1999) – Deuflhard & Weber (2004) – Schutte to speak in Workshop IV • Project dynamics onto subspaces given by A, to find reduced order approximation IPAM, Sept 13, 2005

IPAM, Sept 13, 2005

IPAM, Sept 13, 2005

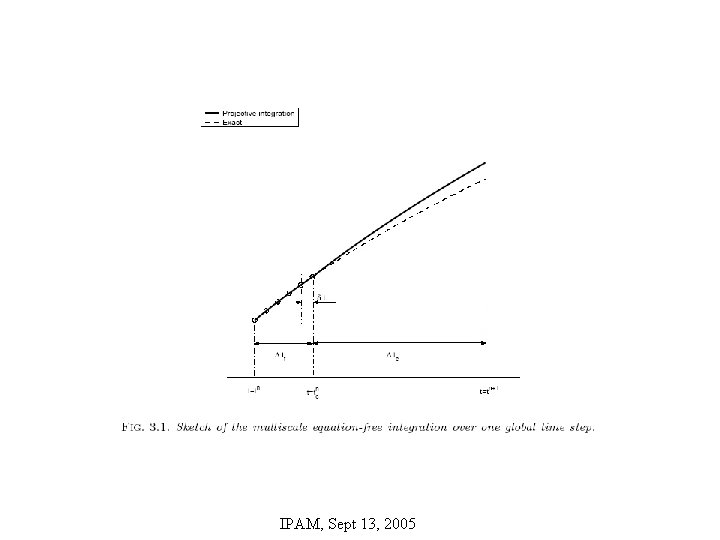
Equation-Free Multiscale Method • For many processes, equations are not readily available – dynamics specified by an algorithm, difficult to write as a set of equations – Legacy computer code • Multiscale modeling and simulation must proceed without use of equations – Method by Kevrekidis and co-workers – Kevrekidis to speak in Caltech workshop following Workshop IV IPAM, Sept 13, 2005

Equation-free multiscale method • Perform small number of fine scale simulations – computationally expensive • Evolution of coarse-grained variables determined by projection – Sensitive to choice of coarse-grained variables – Polynomial expansion used – Perhaps PCCA would be of use IPAM, Sept 13, 2005

IPAM, Sept 13, 2005

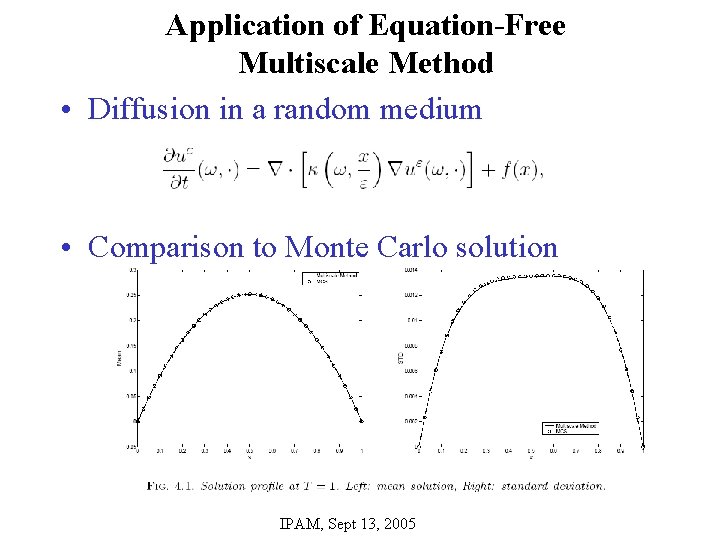
Application of Equation-Free Multiscale Method • Diffusion in a random medium • Comparison to Monte Carlo solution IPAM, Sept 13, 2005

Overview of RGD • Rarefied gas dynamics (RGD) – RGD required when collisional effects are significant – Key step (i. e. computational bottleneck) in many material processing and aerospace simulations – Direct Simulation Monte Carlo (DSMC) is dominant computational method • Boltzmann equation for density function f – ε = Knudsen number = mean free path / characteristic length scale • Applications – Aerospace – Materials processing – MEMS IPAM, Sept 13, 2005

Equilibrium and Fluid Limit of Boltzmann • Maxwellian equilibrium – Q(f, f)=0 implies f=M(v; ρ, u, T) • Equilibration – – Consider f=f(v, t) spatially homogeneous Entropy Boltzmann’s H-theorem implies f →M as t →∞ • Fluid Limit (Hilbert, Grad, Nishida, REC) – ε→ 0 – f(v, x, t)→ M(v; ρ, u, T), with ρ= ρ(x, t), etc. – ρ, u, T satisfy Euler (or Navier-Stokes) IPAM, Sept 13, 2005

Rarefied vs. Continuum Flow: Knudsen number Kn IPAM, Sept 13, 2005

Collisional Effects in the Atmosphere IPAM, Sept 13, 2005

DSMC • DSMC = Direct Simulation Monte Carlo – Invented by Graeme Bird, early 1970’s – Represents density function as collection of particles – Directly simulates RGD by randomizing collisions • Collision v, w →v’, w’ conserving momentum, energy • Relative position of v and w particles is randomized – Particle advection – Convergence (Wagner 1992) • Limitation of DSMC – DSMC becomes computationally intractable near fluid regime, since collision time-scale becomes small IPAM, Sept 13, 2005

Hybrid method • IFMC=Interpolated Fluid Monte Carlo – Combines DSMC and fluid methods – Representation of density function as combination of Maxwellian and particles • • ρ, u, T solved from fluid eqtns, using Boltzmann scheme for CFD N = O(1 - α) α = 0 ↔ DSMC α = 1 ↔ CFD – Remains robust near fluid limit IPAM, Sept 13, 2005

IFMC for Spatially Homogeneous Problem • Implicit time formulation • Thermalization approximation • Hybrid representation IPAM, Sept 13, 2005

Implicit time formulation • From Pareschi’s thesis – related to Bird’s “no time counter” (NTC) method • Collision operator – Rewrite with constant negative term (“trial collision” rate) • Implicit time formulation of Boltzmann – New time variable – Boltzmann equation becomes IPAM, Sept 13, 2005

Thermalization Approximation • Spatially Homogeneous Problem – Wild expansion – fk includes particles having k collisions • Thermalization approximation – Replace particles having 2 or more collisions in time step dt by Maxwellian M – Resulting evolution over dt IPAM, Sept 13, 2005

Hybrid Representation and Evolution • Hybrid representation – g= {particles}, M=Maxwellian, β= equilibration coefficient • Evolution equations – From thermalization approximation – Equations for β and g – g eqtn has Monte Carlo (DSMC) representation IPAM, Sept 13, 2005

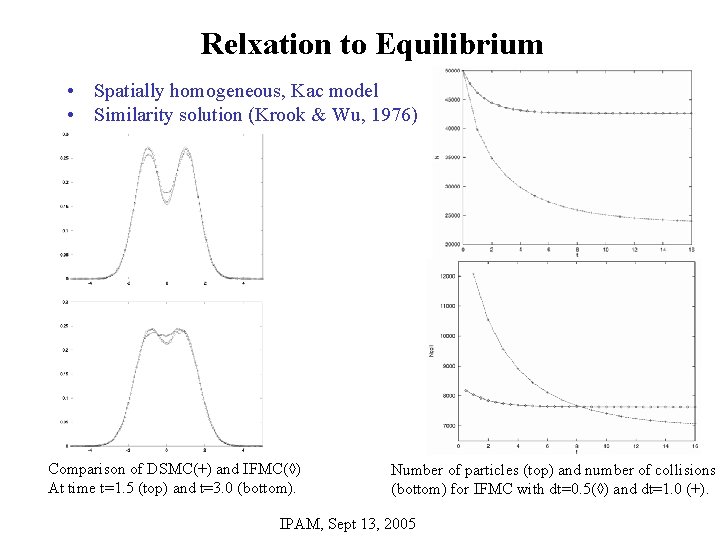
Relxation to Equilibrium • Spatially homogeneous, Kac model • Similarity solution (Krook & Wu, 1976) Comparison of DSMC(+) and IFMC(◊) At time t=1. 5 (top) and t=3. 0 (bottom). Number of particles (top) and number of collisions (bottom) for IFMC with dt=0. 5(◊) and dt=1. 0 (+). IPAM, Sept 13, 2005

IFMC for Spatially Inhomogeneous Problem • Time splitting • Collision step as above – Because of disequilibrium from advection, start with β=0 • Convection step: 2 methods – Move particles by their velocity – Move continuum part: 2 methods • Direct convection of Maxwellians • Use of Euler or Navier-Stokes equations for convection IPAM, Sept 13, 2005

Computational Results • Shock • Leading Edge problem – Flow past half-infinite flat plate • Flow past wedge IPAM, Sept 13, 2005

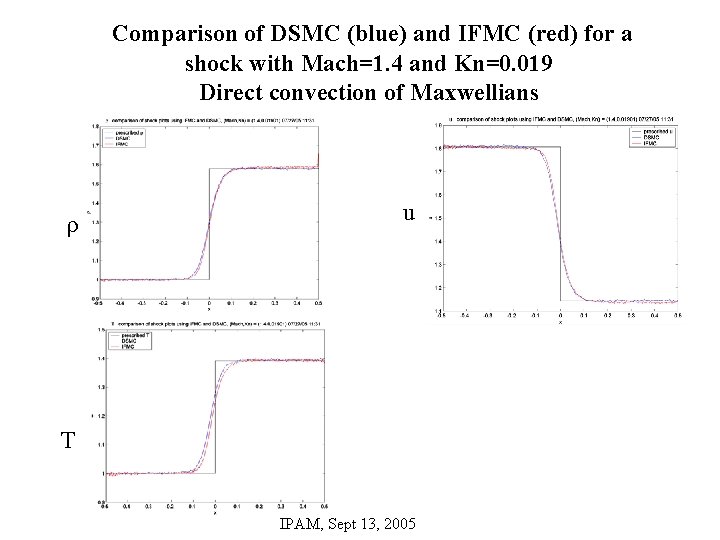
Comparison of DSMC (blue) and IFMC (red) for a shock with Mach=1. 4 and Kn=0. 019 Direct convection of Maxwellians ρ u T IPAM, Sept 13, 2005

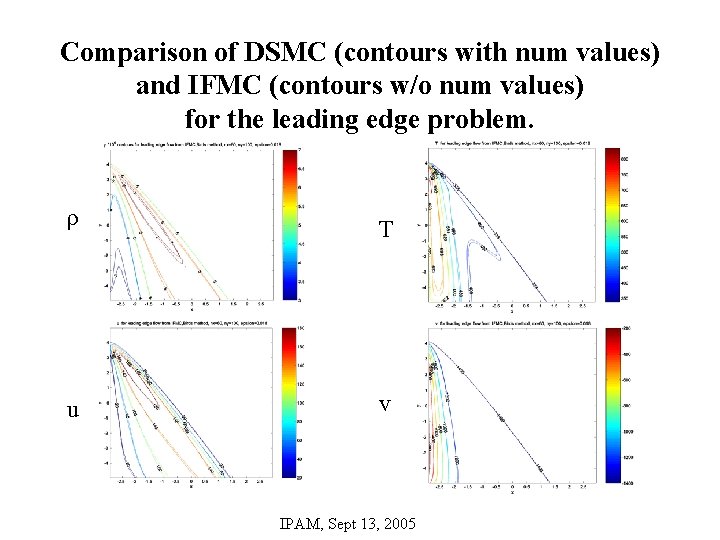
Comparison of DSMC (contours with num values) and IFMC (contours w/o num values) for the leading edge problem. ρ T u v IPAM, Sept 13, 2005

Conclusions and Prospects • Hybrid method for RGD that performs uniformly in the fluid and near-fluid regime • Applications to aerospace, materials, MEMS • Current development – Generalized numerics, physics, geometry – Test problems IPAM, Sept 13, 2005