Multiscale Modeling An Overview Dr Mark Horstemeyer CAVS

Multiscale Modeling: An Overview Dr. Mark Horstemeyer CAVS Chair Professor ASME Fellow Mississippi State University mfhorst@me. msstate. edu 662. 325. 5449

Outline 1) Modeling Philosophy Overview 2) MSU Internal State Variable Plasticity-Damage Model (MSU DMG 1. 0) Theory 1) Horstemeyer, M. F. , Lathrop, J. , Gokhale, A. M. , and Dighe, M. , “Modeling Stress State Dependent Damage Evolution in a Cast Al-Si-Mg Aluminum Alloy, ” Theoretical and Applied Fracture Mechanics, Vol. 33, pp. 31 -47, 2000 2) Bammann, D. J. , Chiesa, M. L. , Horstemeyer, M. F. , Weingarten, L. I. , "Failure in Ductile Materials Using Finite Element Methods, " Structural Crashworthiness and Failure, eds. T. Wierzbicki and N. Jones, Elsevier Applied Science, The Universities Press (Belfast) Ltd, 1993. 3) Image Analysis Tool 1. 0 User’s Tutorial 4) DMGfit 1. 0 User’s Tutorial 5) MSU Multi. Stage Fatigue Model (MSU MSF 1. 0) Theory 1) Mc. Dowell, D. L. , Gall, K. , Horstemeyer, M. F. , and Fan, J. , “Microstructure-Based Fatigue Modeling of Cast A 356 -T 6 Alloy, ” Engineering Fracture Mechanics, Vol. 70, pp. 49 -80, 2003. 6) MSFfit 1. 0 User’s Tutorial 7) MSU ISV Thermoplastic Model (MSU TP 1. 0) Theory 1) J. L. Bouvard, D. K. Ward, D. Hossain, E. B. Marin, D. J. Bammann, and M. F. Horstemeyer, “A General Inelastic Internal State Variable Model for Amorphous Glassy Polymers, ” submitted to Acta Mechanica 8) TPfit 1. 0 User’s Tutorial

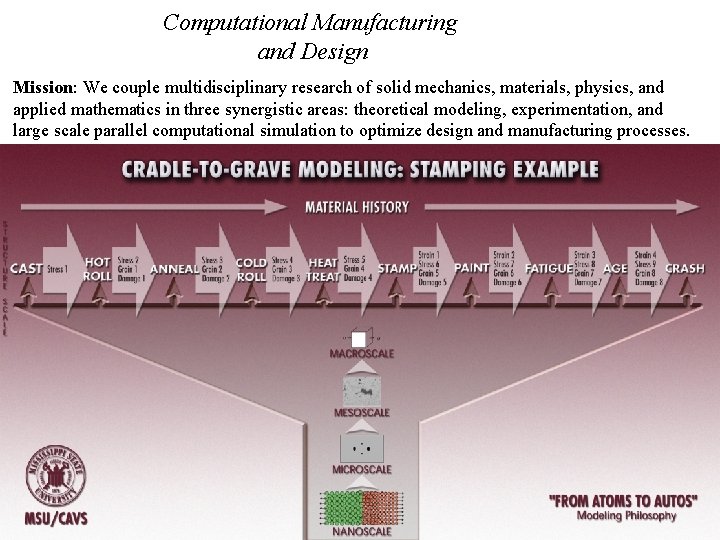
Computational Manufacturing and Design Mission: We couple multidisciplinary research of solid mechanics, materials, physics, and applied mathematics in three synergistic areas: theoretical modeling, experimentation, and large scale parallel computational simulation to optimize design and manufacturing processes.

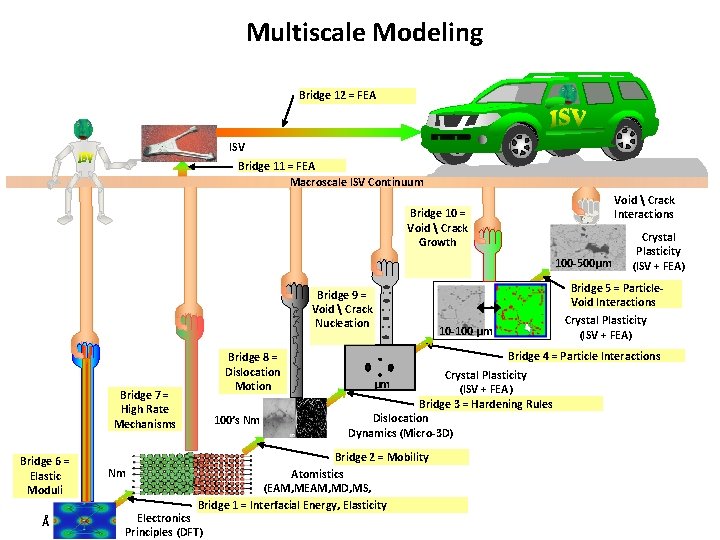
Multiscale Modeling Bridge 12 = FEA ISV Bridge 11 = FEA Macroscale ISV Continuum Void Crack Interactions Bridge 10 = Void Crack Growth 100 -500µm Bridge 5 = Particle. Void Interactions Bridge 9 = Void Crack Nucleation Bridge 8 = Dislocation Motion Bridge 7 = High Rate Mechanisms Bridge 6 = Elastic Moduli Å Nm 100’s Nm Crystal Plasticity (ISV + FEA) 10 -100 µm Bridge 4 = Particle Interactions Crystal Plasticity (ISV + FEA) Bridge 3 = Hardening Rules Dislocation Dynamics (Micro-3 D) µm Bridge 2 = Mobility Atomistics (EAM, MD, MS, Bridge 1 = Interfacial Energy, Elasticity Electronics Principles (DFT) Crystal Plasticity (ISV + FEA)

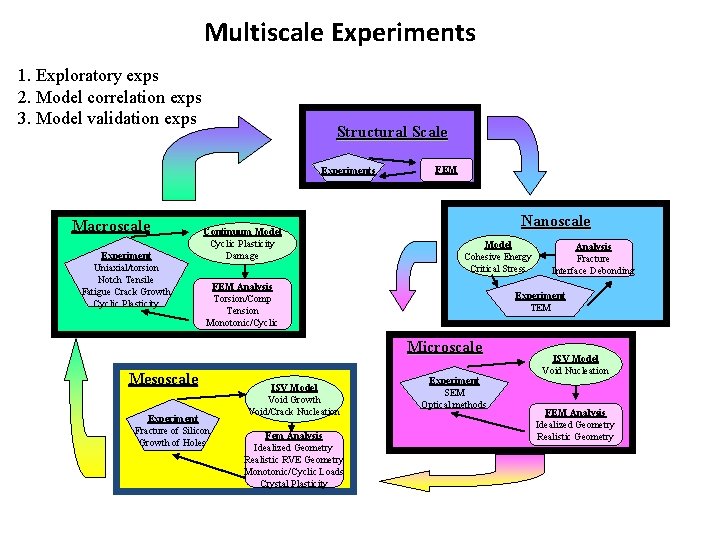
Multiscale Experiments 1. Exploratory exps 2. Model correlation exps 3. Model validation exps Structural Scale Experiments Macroscale Experiment Uniaxial/torsion Notch Tensile Fatigue Crack Growth Cyclic Plasticity Continuum Model Cyclic Plasticity Damage FEM Nanoscale Model Cohesive Energy Critical Stress FEM Analysis Torsion/Comp Tension Monotonic/Cyclic Experiment TEM Microscale Mesoscale Experiment Fracture of Silicon Growth of Holes IVS Model ISV Model Void. Growth Void/Void Coalescence Void/Crack Nucleation Void/Particle Coalescence Fem Analysis Idealized Geometry Realistic RVE Geometry Monotonic/Cyclic Loads Crystal Plasticity Analysis Fracture Interface Debonding Experiment SEM Optical methods ISV Model Void Nucleation FEM Analysis Idealized Geometry Realistic Geometry

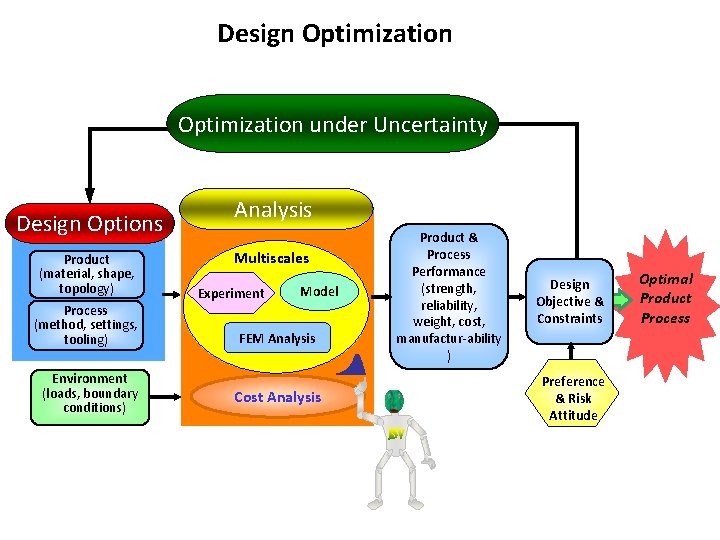
Design Optimization under Uncertainty Design Options Product (material, shape, topology) Process (method, settings, tooling) Environment (loads, boundary conditions) Analysis Multiscales Experiment Model FEM Analysis Cost Analysis Product & Process Performance (strength, reliability, weight, cost, manufactur-ability ) Design Objective & Constraints Preference & Risk Attitude Optimal Product Process

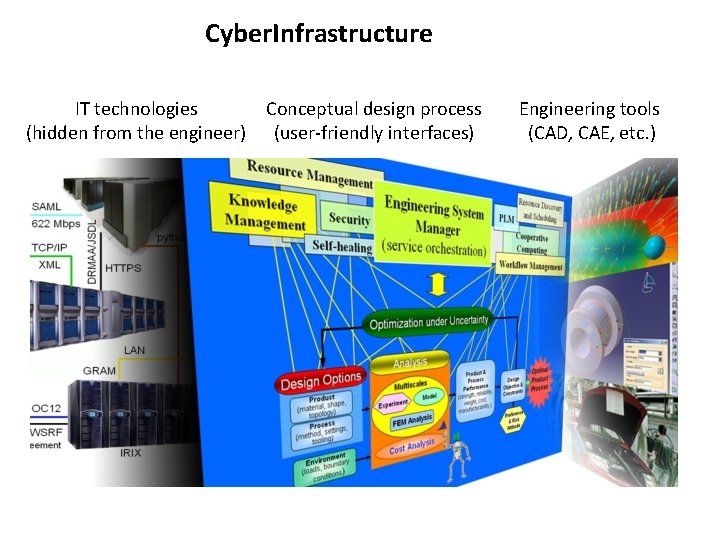
Cyber. Infrastructure IT technologies Conceptual design process (hidden from the engineer) (user-friendly interfaces) Engineering tools (CAD, CAE, etc. )

GM CADILLAC CONTROL ARM LIGHTWEIGHT DESIGN (2000) B C Objective: To employ multiscale material modeling to reduce the weight of components D E Wrong! A Truth! Standard FEA Inclusion Damage Stress (from highest (from most severe to less severe) to lowest) B A D E D A A E C D C E C B B model Region 1 Region 3 (a) initial failure site (b) experiment Result: To optimize a redesign such that 25% weight saved 50% increase in load-bearing capacity 100% increase in fatigue life $2 less per part

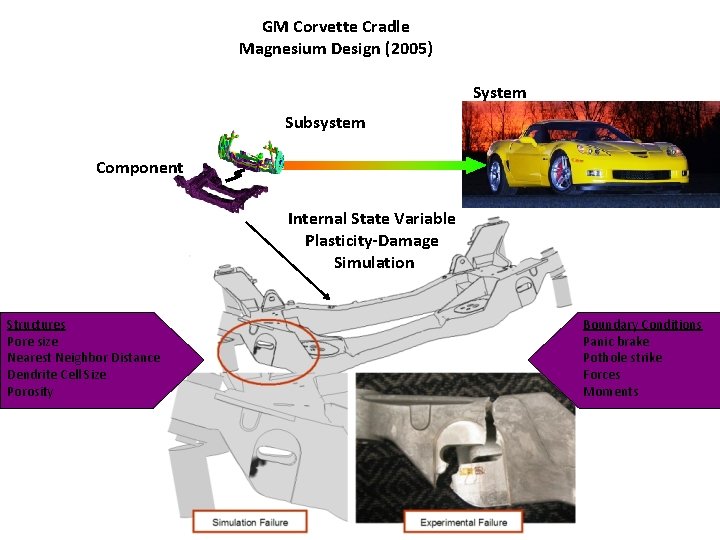
GM Corvette Cradle Magnesium Design (2005) System Subsystem Component Internal State Variable Plasticity-Damage Simulation Structures Pore size Nearest Neighbor Distance Dendrite Cell Size Porosity Boundary Conditions Panic brake Pothole strike Forces Moments

Cradle Load-to-Failure Simulation Results E D C B A F Modern FEA answer Modern Materials Science answer True answer

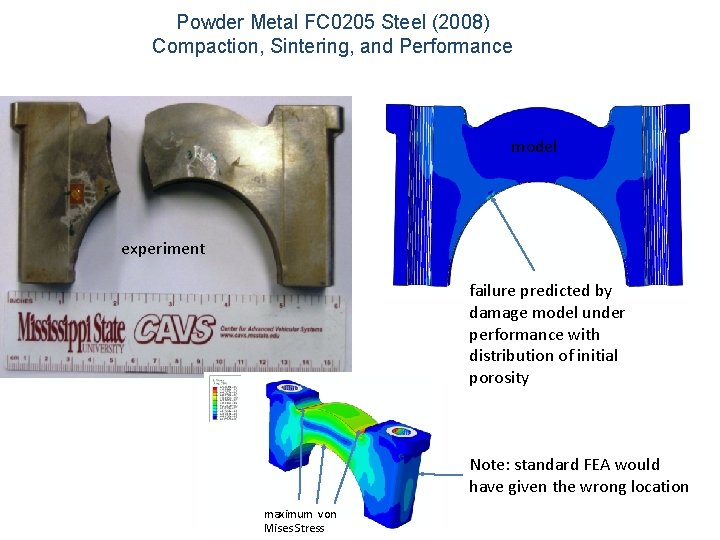
Powder Metal FC 0205 Steel (2008) Compaction, Sintering, and Performance model experiment failure predicted by damage model under performance with distribution of initial porosity Note: standard FEA would have given the wrong location maximum von Mises Stress

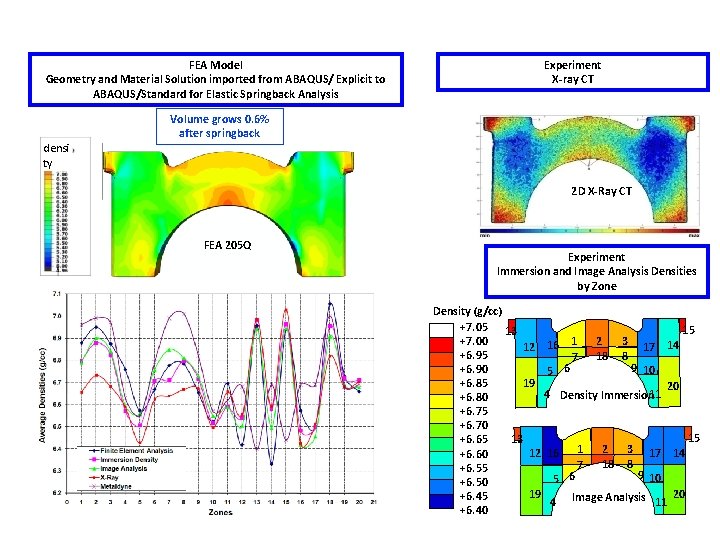
I – Compaction Modeling (Validation) Main Bearing Cap – Green Density Distribution- after Springback (g/cc) FEA Model Geometry and Material Solution imported from ABAQUS/ Explicit to ABAQUS/Standard for Elastic Springback Analysis Experiment X-ray CT Volume grows 0. 6% after springback densi ty 2 D X-Ray CT FEA 205 Q Experiment Immersion and Image Analysis Densities by Zone Density (g/cc) +7. 05 13 15 +7. 00 1 2 3 12 16 17 14 +6. 95 18 8 7 9 10 +6. 90 5 6 19 +6. 85 20 4 Density Immersion 11 +6. 80 +6. 75 +6. 70 15 13 +6. 65 1 2 3 12 16 17 14 +6. 60 18 8 7 +6. 55 9 10 5 6 +6. 50 19 20 +6. 45 4 Image Analysis 11 +6. 40

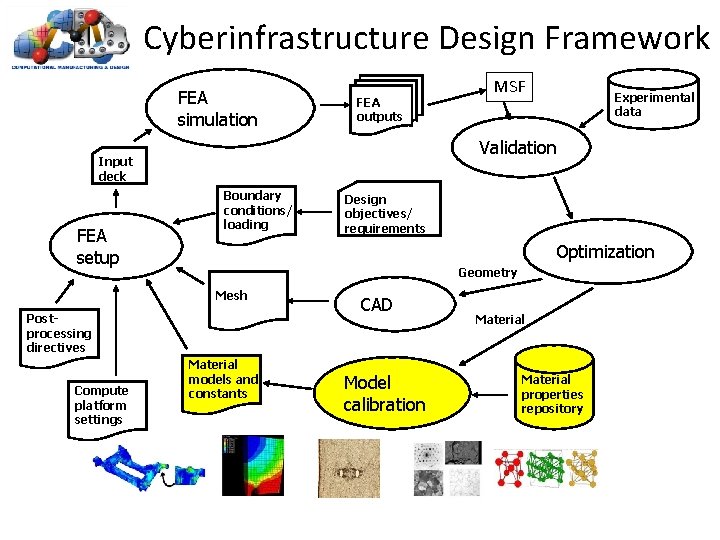
Cyberinfrastructure Design Framework FEA simulation FEA outputs Boundary conditions/ loading Design objectives/ requirements Optimization Geometry Mesh Postprocessing directives Compute platform settings Experimental data Validation Input deck FEA setup MSF Material models and constants CAD Model calibration Material properties repository

MSU Multiscale Modeling • Vision: In 5 -10 years, we are internationally recognized as the premiere material modeling group in world for our validated and verified research and production models • Mission: systemize our multiscale modeling capability so that the cyberinfrastructure easily admits each different aspect of the modeling characteristics (codes, materials info, mechanical properties tests, multiscale models, etc)

Modeling History and Overview • Started in thermonuclear weapons design at Sandia (no underground systems level testing) • Populate the space of systems levels with simulations (simulation based design and multiscale modeling to get correct physics) • Used for many different metal alloys in materials processing and life-performance analysis • Tech transfer to Navy, Army, and automotive applications • Notion of history modeling with internal state variables

FEA Simulations and Timeline Using Internal State Variable Model • Early 1980’s: steel alloys for weapon laydown event (highlight: front cover of Science) plasticity, damage, and fracture • Mid 1980’s-1990’s: forging process: rex • Late 1980’s: analysis of various components: plasticity and failure • Early 1990’s: Navy submarines lethality, welding • Mid 1990’s: forming, extrusion, heat treatment • Late 1990’s: automotive castings • Early 2000’s: everything automotive • Mid 2000’s: Army vehicle component designs • Late 2000’s: polymers and powder metals

Metals Modeled by Macroscale DMG ISV Plasticity-Damage Model 1. 0 • Steel Alloys (15) – A 286, AF, C 1008, S 7 tool, 1020, 10 b 22, 4140, 4340, 210 SS, 304 LSS, 319 SS, HY 80, HY 100, HY 130, FC 0205 • Aluminum Alloys(16) – 1100, 2024 T 35, 2024 T 4, 5083, 5086, 6061 T 0, 6022, 6050, 6061 T 6, 7039, 7075 T 0, 7075 T 6, A 319, A 356 • Magnesium Alloys (7) – AM 20, AM 30, AM 50, AM 60, AZ 31, AZ 91, AE 44 • Titanium Alloys (4) – Ti 7 Al 4 Mo, Ti 8 Al 1 Mo 1 V, Ti 0 Al 6 V 4, Ti 6 Al 6 V 2 Sn • Uranium Alloys (2) – D 38, D 380075 Ti • Nickel (2) – 99. 99% pure, In 718 • Brass (1) – 99% pure 70 metal alloys to date!

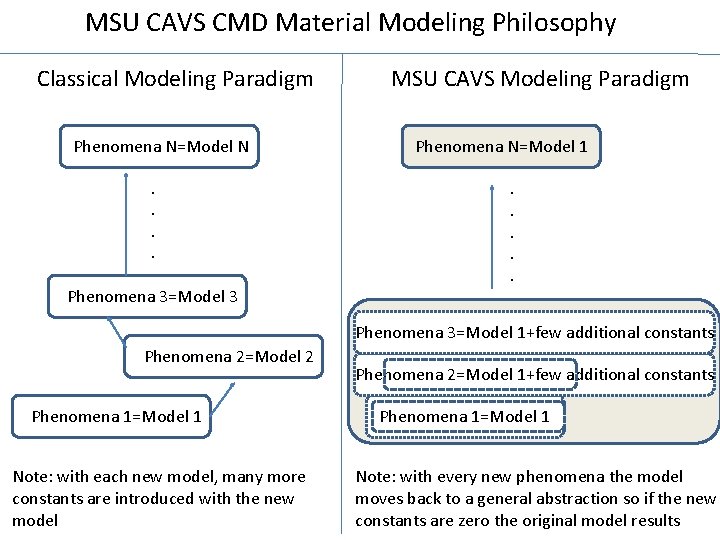
MSU CAVS CMD Material Modeling Philosophy Classical Modeling Paradigm Phenomena N=Model N. . Phenomena 3=Model 3 MSU CAVS Modeling Paradigm Phenomena N=Model 1. . . Phenomena 3=Model 1+few additional constants Phenomena 2=Model 2 Phenomena 1=Model 1 Note: with each new model, many more constants are introduced with the new model Phenomena 2=Model 1+few additional constants Phenomena 1=Model 1 Note: with every new phenomena the model moves back to a general abstraction so if the new constants are zero the original model results

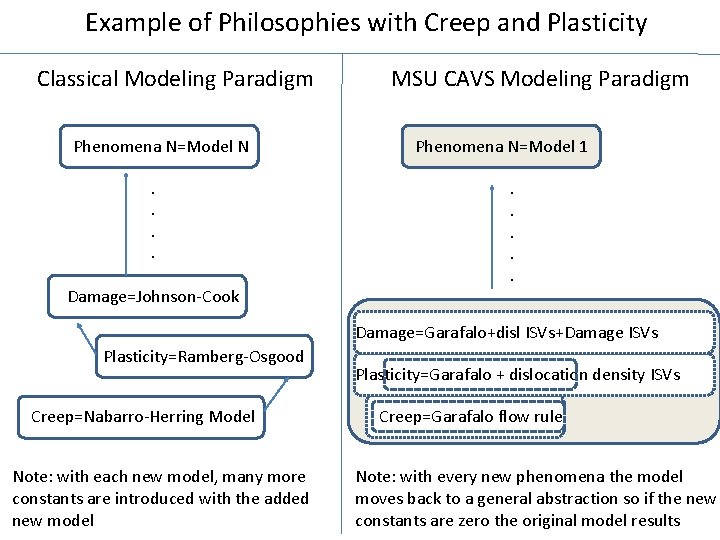
Example of Philosophies with Creep and Plasticity Classical Modeling Paradigm Phenomena N=Model N. . Damage=Johnson-Cook MSU CAVS Modeling Paradigm Phenomena N=Model 1. . . Damage=Garafalo+disl ISVs+Damage ISVs Plasticity=Ramberg-Osgood Creep=Nabarro-Herring Model Note: with each new model, many more constants are introduced with the added new model Plasticity=Garafalo + dislocation density ISVs Creep=Garafalo flow rule Note: with every new phenomena the model moves back to a general abstraction so if the new constants are zero the original model results

Macroscale Research and Production Models Note 1: Production models/codes must have a documented citable journal article for each version of the code a. makes impact factor greater b. makes it easier for next graduate student to add incremental improvements Note 2: Production models/codes must build on the previous work a. helps systemize and synergize our efforts in terms of research and funding b. clears up confusion to outsider customers and industry c. helps user base Note 3: Production models/codes must have a theoretical and user’s manual a. absolute necessity for new graduate students and new user’s b. helps the broad usage of the model over time c. this alone may lead the greatest impact over time Note 4: Only a Production model/code can go into the cyberinfrastructure

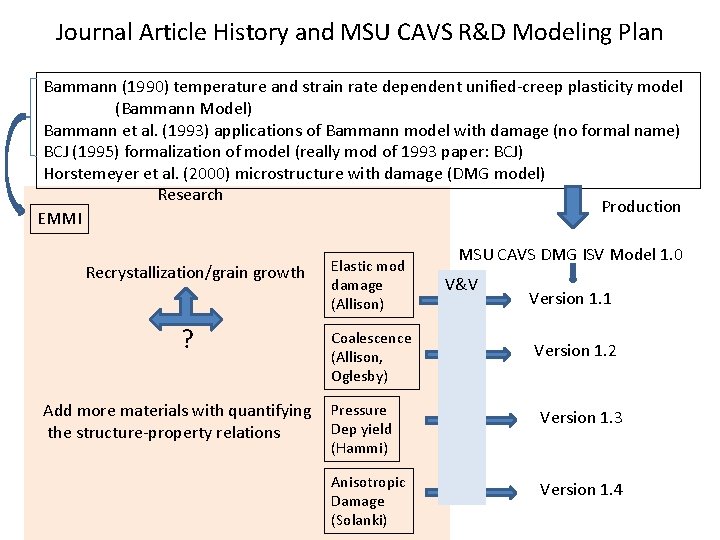
Journal Article History and MSU CAVS R&D Modeling Plan Bammann (1990) temperature and strain rate dependent unified-creep plasticity model (Bammann Model) Bammann et al. (1993) applications of Bammann model with damage (no formal name) BCJ (1995) formalization of model (really mod of 1993 paper: BCJ) Horstemeyer et al. (2000) microstructure with damage (DMG model) Research Production EMMI Recrystallization/grain growth ? Add more materials with quantifying the structure-property relations Elastic mod damage (Allison) Coalescence (Allison, Oglesby) MSU CAVS DMG ISV Model 1. 0 V&V Version 1. 1 Version 1. 2 Pressure Dep yield (Hammi) Version 1. 3 Anisotropic Damage (Solanki) Version 1. 4

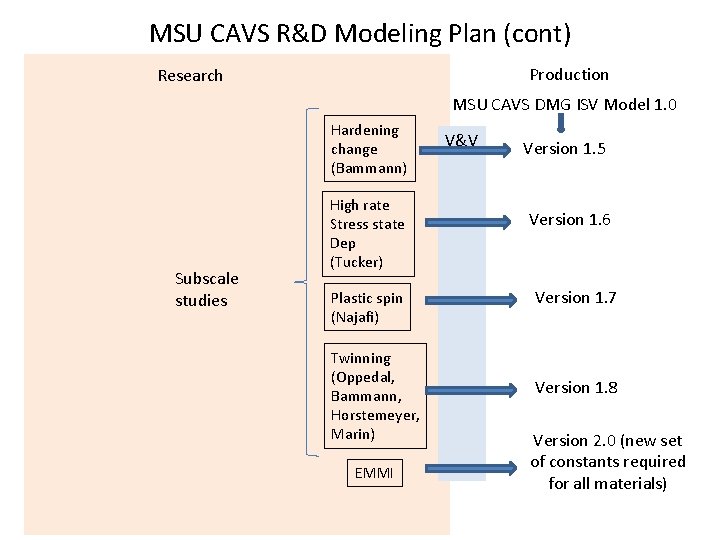
MSU CAVS R&D Modeling Plan (cont) Production Research MSU CAVS DMG ISV Model 1. 0 Hardening change (Bammann) Subscale studies High rate Stress state Dep (Tucker) Plastic spin (Najafi) Twinning (Oppedal, Bammann, Horstemeyer, Marin) EMMI V&V Version 1. 5 Version 1. 6 Version 1. 7 Version 1. 8 Version 2. 0 (new set of constants required for all materials)

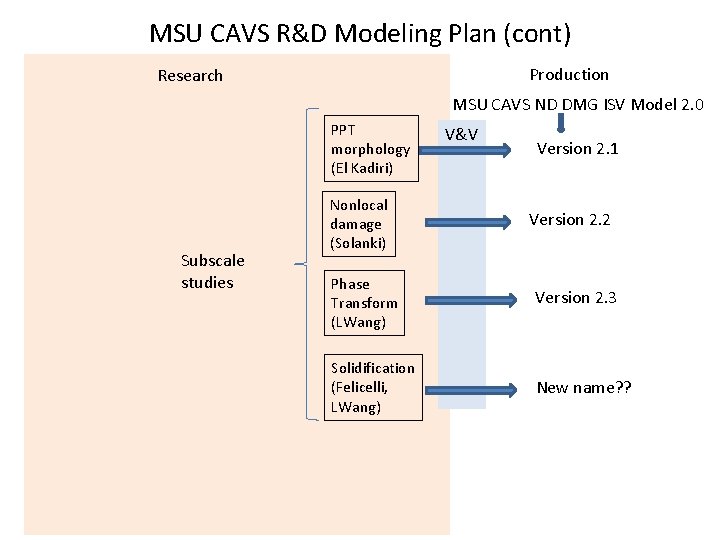
MSU CAVS R&D Modeling Plan (cont) Production Research MSU CAVS ND DMG ISV Model 2. 0 PPT morphology (El Kadiri) Subscale studies Nonlocal damage (Solanki) V&V Version 2. 1 Version 2. 2 Phase Transform (LWang) Version 2. 3 Solidification (Felicelli, LWang) New name? ?

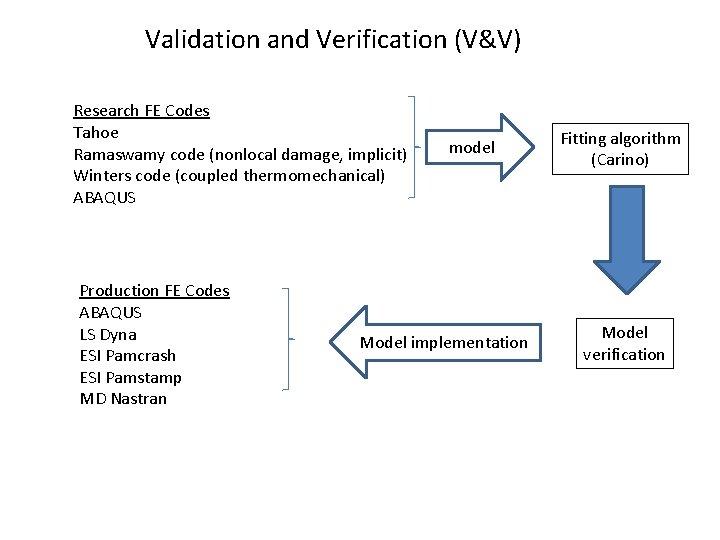
Validation and Verification (V&V) Research FE Codes Tahoe Ramaswamy code (nonlocal damage, implicit) Winters code (coupled thermomechanical) ABAQUS Production FE Codes ABAQUS LS Dyna ESI Pamcrash ESI Pamstamp MD Nastran model Model implementation Fitting algorithm (Carino) Model verification

Metals Modeled by Multi. Stage Fatigue Model 1. 0 • Steel Alloys (3) – 4140, 319 SS, FC 0205 • Aluminum Alloys(5) – 2024 T 0, 7075 T 6, A 319, A 356, A 380 • Magnesium Alloys (7) 15 metal alloys to date! – AM 30, AM 50, AM 60, AZ 31, AZ 61, AZ 91, AE 44 Polymers Modeled by Multi. Stage Fatigue Model 1. 0 • Polyurethane (2) – Pure, carbon nanotube polyurethane • Elastomer (2) – SBR, track rubber • Polycarbonate (1)

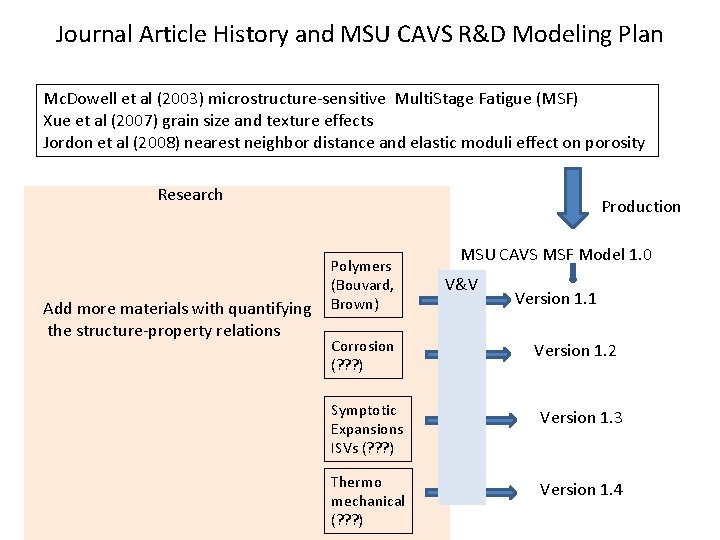
Journal Article History and MSU CAVS R&D Modeling Plan Mc. Dowell et al (2003) microstructure-sensitive Multi. Stage Fatigue (MSF) Xue et al (2007) grain size and texture effects Jordon et al (2008) nearest neighbor distance and elastic moduli effect on porosity Research Add more materials with quantifying the structure-property relations Production Polymers (Bouvard, Brown) Corrosion (? ? ? ) MSU CAVS MSF Model 1. 0 V&V Version 1. 1 Version 1. 2 Symptotic Expansions ISVs (? ? ? ) Version 1. 3 Thermo mechanical (? ? ? ) Version 1. 4

• • • Polymers Modeled by Macroscale ISV Visco. Elastic-Visco. Plasticity-Damage Model 1. 0 Polycarbonate (1) Polypropylene (1) Polyurethane (1) ABS Elastomer (3 -Santoprene, natural rubber, SBR) Nylon (4) – Nylon 6. 6, Nylon 4. 4, E-glass+Nylon, S-glass+Nylon Kevlar Brain Liver Tendon Placenta 12 polymers to date!

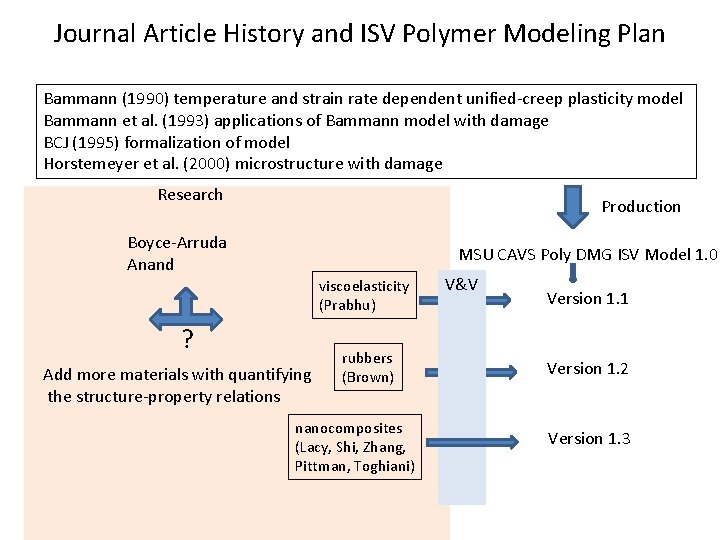
Journal Article History and ISV Polymer Modeling Plan Bammann (1990) temperature and strain rate dependent unified-creep plasticity model Bammann et al. (1993) applications of Bammann model with damage BCJ (1995) formalization of model Horstemeyer et al. (2000) microstructure with damage Research Production Boyce-Arruda Anand MSU CAVS Poly DMG ISV Model 1. 0 viscoelasticity (Prabhu) ? Add more materials with quantifying the structure-property relations rubbers (Brown) nanocomposites (Lacy, Shi, Zhang, Pittman, Toghiani) V&V Version 1. 1 Version 1. 2 Version 1. 3

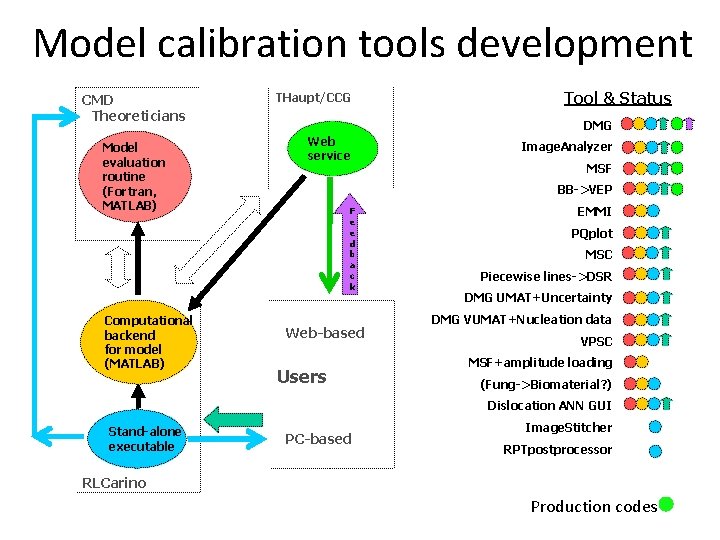
Model calibration tools development CMD Theoreticians Model evaluation routine (Fortran, MATLAB) Computational backend for model (MATLAB) THaupt/CCG Tool & Status DMG Web service Image. Analyzer MSF BB->VEP F e e d b a c k Web-based Users EMMI PQplot MSC Piecewise lines->DSR DMG UMAT+Uncertainty DMG VUMAT+Nucleation data VPSC MSF+amplitude loading (Fung->Biomaterial? ) Dislocation ANN GUI Stand-alone executable PC-based Image. Stitcher RPTpostprocessor RLCarino Production codes

Model code, Providers, Users mfhorst (various), S. Agnew, Y. Guo tnw 7 (various) mfhorst, bjordan yhammi, bjordon, paul, adrian BB->VEP jeanluc, jef 83 EMMI ebmarin jcrapps PQplot yhammi (USAMP-PM? ) MSC yhammi (USAMP-PM? ) (jeanluc) sponder DMG UMAT+Uncertainty kns 3 DMG VUMAT+Nucl. data kns 3 aoppedal, haitham aoppedal Mfhorst, bjordan (NGC? ) (lwilliams) ? El. Kadiri osama, (haitham’s student) DMG Image. Analyzer MSF Piecewise curves->DSR VPSC MSF+amplitude loading (Fung->Biomaterial? ) Dislocation ANN GUI Image. Stitcher RPTpostprocessor Production codes (bjordon) (axue’s student)

Computational Manufacturing and Design Mission: We couple multidisciplinary research of solid mechanics, materials, physics, and applied mathematics in three synergistic areas: theoretical modeling, experimentation, and large scale parallel computational simulation to optimize design and manufacturing processes.