Multiresolution Analysis CS 474674 Prof Bebis Multiresolution Analysis

Multiresolution Analysis CS 474/674 – Prof. Bebis

Multiresolution Analysis • Many signals or images contain information at different scales or levels of detail (e. g. , people vs buildings) • Analyzing information at the same scale will not be effective. Use windows of different size (i. e. , vary scale)

Multiresolution Analysis (cont’d) Alternatively, use the same window size but analyze information at different resolutions: Small size objects should be examined at a high resolution High resolution Low resolution Large size objects should be examined at a low resolution

Multiresolution Analysis (cont’d) • We will review two techniques for representing multiresolution information efficiently: – Pyramidal coding – Subband coding

Image Pyramids A collection of decreasing resolution images arranged in the shape of a pyramid.

Image Pyramids (cont’d) (high scale) low resolution j=0 (low scale) high resolution j = J Example: if N=256, there will be 8+1=9 levels
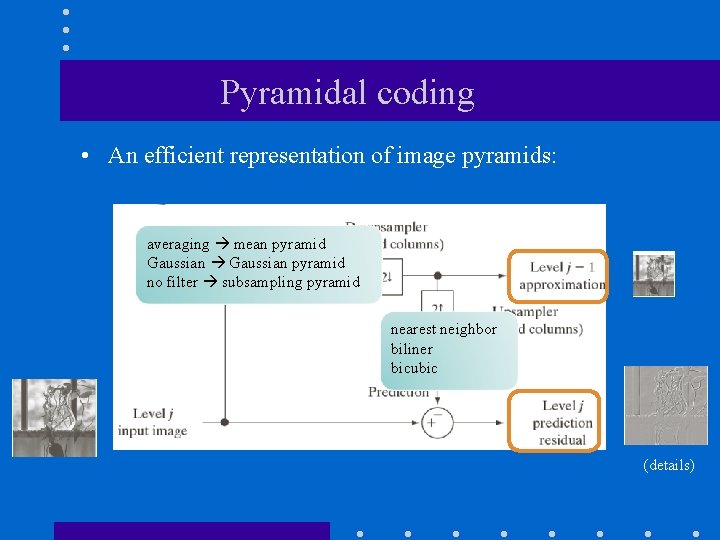
Pyramidal coding • An efficient representation of image pyramids: averaging mean pyramid Gaussian pyramid no filter subsampling pyramid nearest neighbor biliner bicubic (details)

Pyramidal coding (cont’d) Approximation pyramid (based on Gaussian filter) Prediction residual pyramid (based on bilinear interpolation) Note: the last level is the same as that of the approximation pyramid

Pyramidal coding (cont’d) In the absence of quantization errors, the approximation pyramid can be re-constructed from the prediction residual pyramid. (details) • We only need to keep the prediction residual pyramid only! - More efficient representation

Pyramidal coding (cont’d) Just add the “details” or “residual error” back! + Up-sample & Interpolate (details)

Subband coding • Decompose an image (or signal) into different frequency bands (analysis step). • Decomposition is performed so that the subbands can be re-assembled to reconstruct the original image without error (synthesis step) • Need to choose appropriate filters (i. e. , “filter bank”)
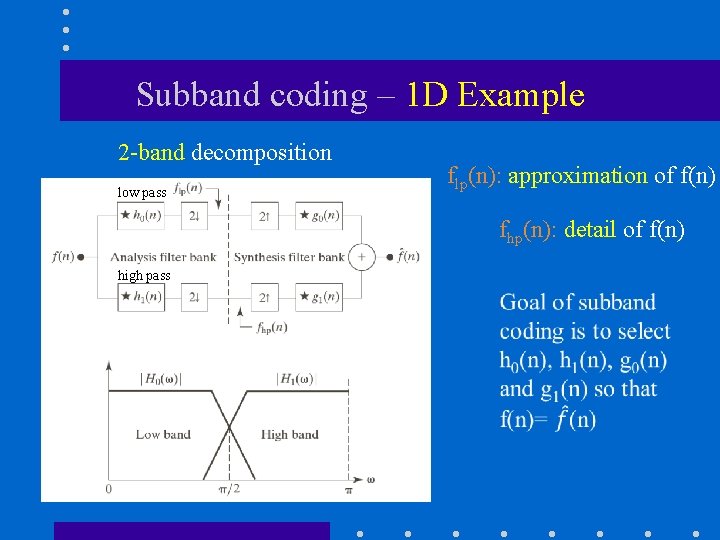
Subband coding – 1 D Example 2 -band decomposition low pass flp(n): approximation of f(n) fhp(n): detail of f(n) high pass
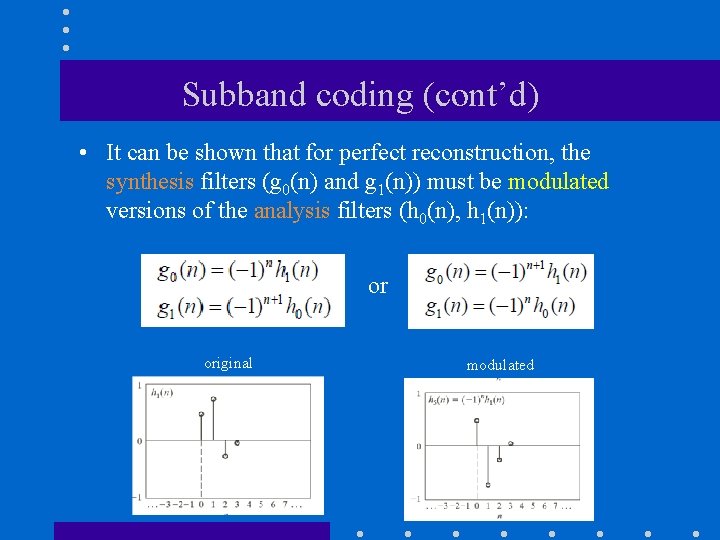
Subband coding (cont’d) • It can be shown that for perfect reconstruction, the synthesis filters (g 0(n) and g 1(n)) must be modulated versions of the analysis filters (h 0(n), h 1(n)): or original modulated

Subband coding (cont’d) • An orthonormal filter bank can be designed from one prototype filter: (non-orthonormal filters require two prototype filters)
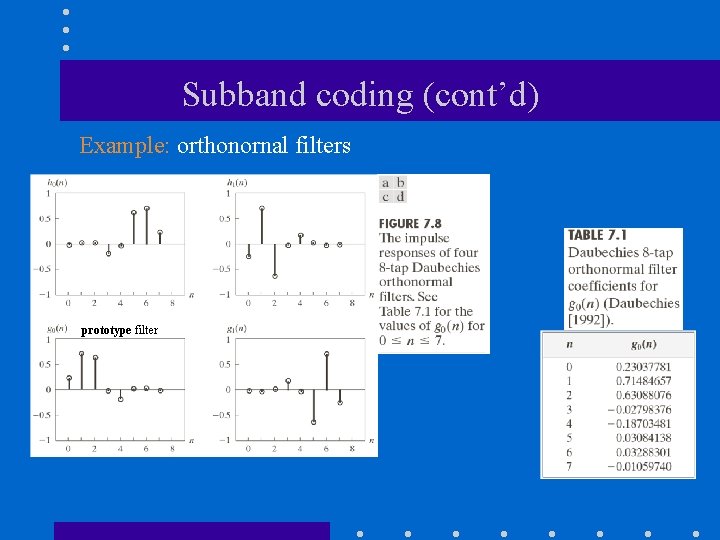
Subband coding (cont’d) Example: orthonornal filters prototype filter
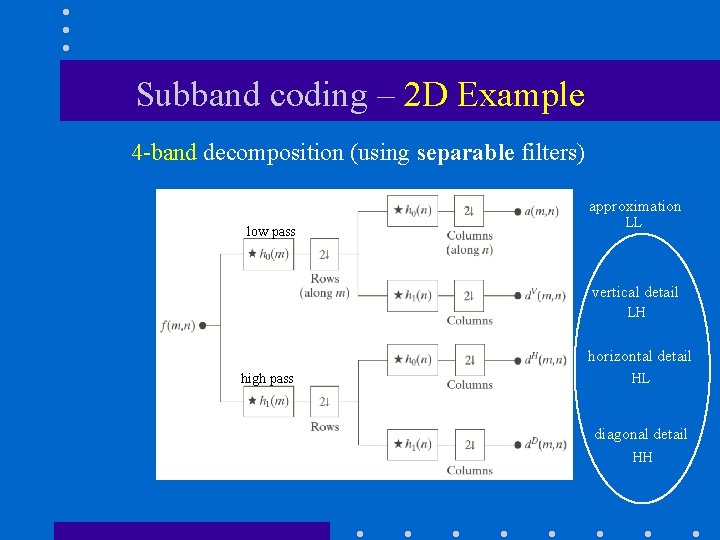
Subband coding – 2 D Example 4 -band decomposition (using separable filters) approximation low pass LL vertical detail LH horizontal detail high pass HL diagonal detail HH

Subband coding (cont’d) approximation vertical detail horizontal detail diagonal detail
- Slides: 17