Multiqubit Entanglement and Quantum Phase Transition in the

Multi-qubit Entanglement and Quantum Phase Transition in the Transverse Ising Model Afshin Montakhab and Ali Asadian Physics Department Shiraz University, Shiraz, Iran

Overview o Multi-qubit entanglement properties of Ising ground state 1. 2. 3. o Global entanglement Genuine multi-qubit entanglement Entanglement sharing of the ground state Conclusion and future development

The Model We study the transverse Ising model: and its higher dimensional generalizations

Entanglement properties of the Ising ground state The ground state of transverse Ising model in zero magnetic field is two-fold degenerate. Coherent superposition of the above states:

o o Previous authors have studied entanglement properties of the ground product states. (e. g. Osborne Nielsen PRA 2002) We study the entanglement properties of GHZ ground state.

Global Entanglement o Informational approach to multi-qubit entanglement Brukner-Zeilinger principle: the total information of one qubit is one bit and the total information of N-qubit system is N bit (for pure states) The total information content of a multi-qubit system can be distributed in local and non-local form

A qubit carries of local information which is one bit for an isolated qubit and N qubit carries of local information

according to information distribution S linear entropy
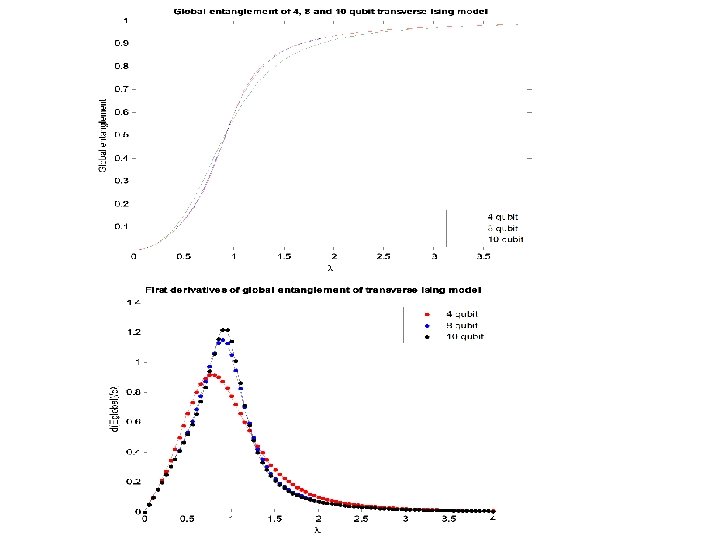
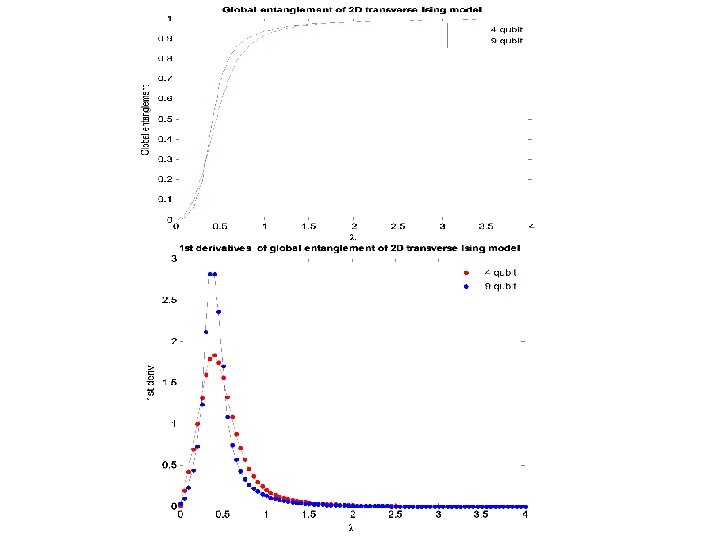
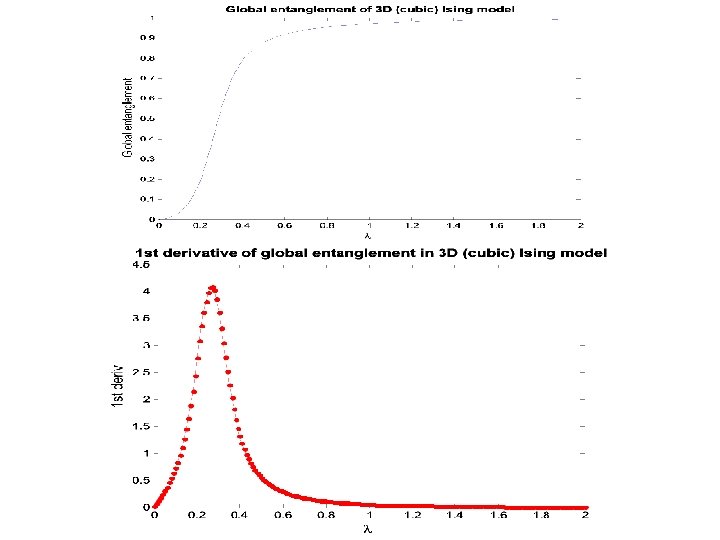

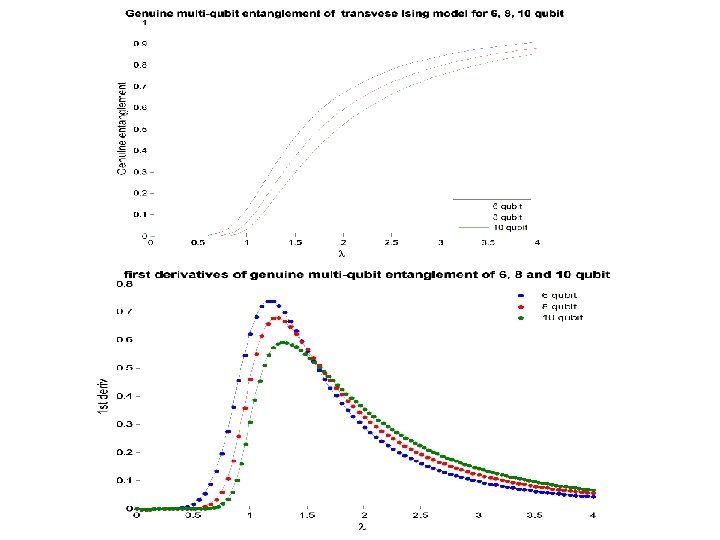
Genuine multi-qubit entanglement Genuine Entanglement is a form of non-local information which is shared by all the constituents of the system. For a pure state of N qubit, when N is even, there are even and odd bipartitions. Information-theoretic measure: Algebraic measure:
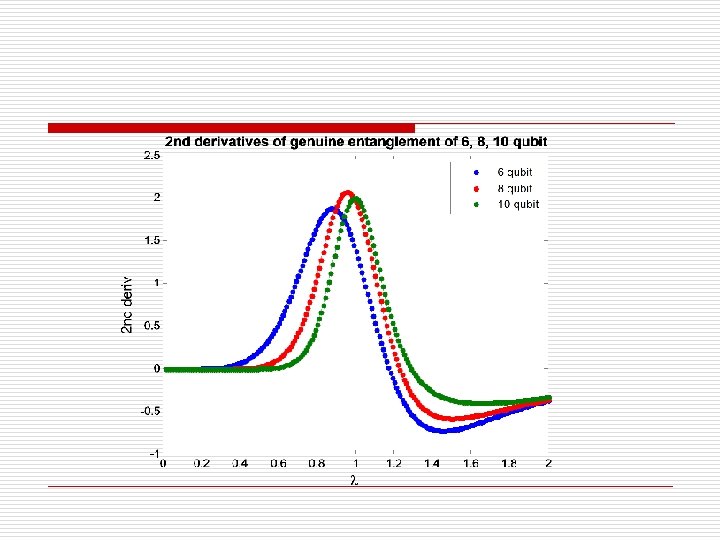
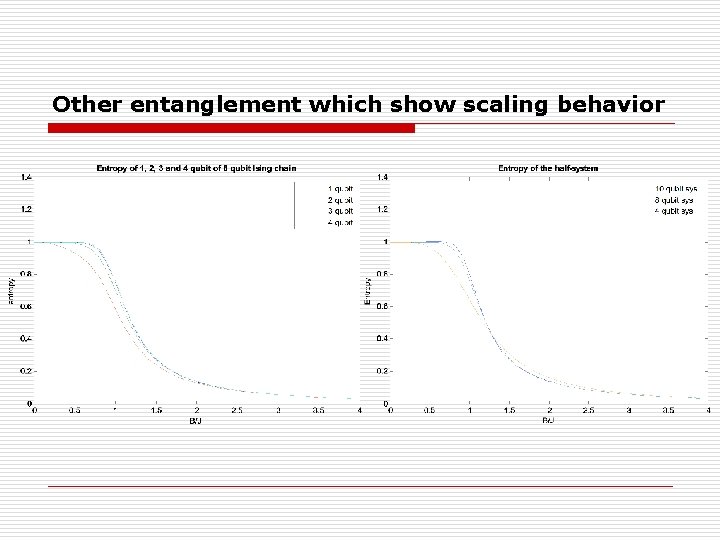
Other entanglement which show scaling behavior

GHZ and decoherence o The GHZ state is often excluded in studies with thermodynamical limit due to decoherence which can lead to product state

The solid line is single-qubit entropy of thermal ground state and the dashed line is single-qubit entropy (global entanglement) of

Entanglement sharing of the ground state Genuine three-qubit entanglement of four-qubit system in pure state We derive this formula from monogamy of entanglement and information distribution in a four-qubit system in pure state. Note that this reduces to KBW tangle if we isolate the fourth qubit i. e. ,
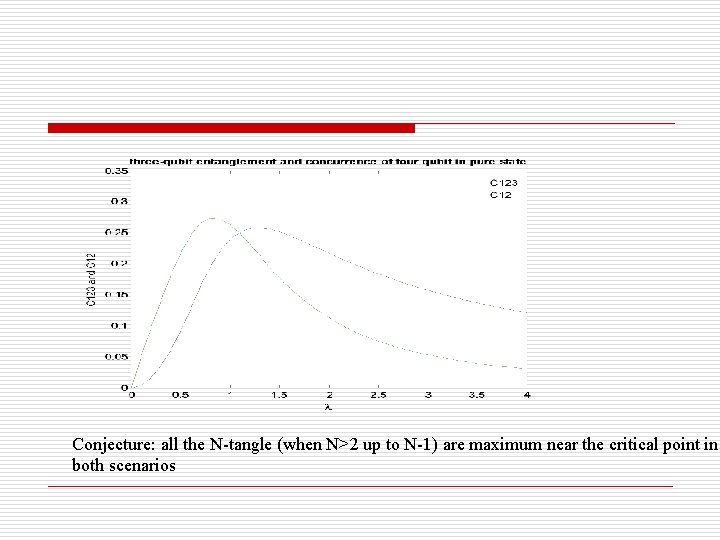
Conjecture: all the N-tangle (when N>2 up to N-1) are maximum near the critical point in both scenarios

Conclusion and future development We study the entanglement properties of the GHZ like state of the Ising ground state. Thermodynamical behavior of entanglement is observed near critical point for global entanglement, reminiscent of classical phase transition. Genuine entanglement is more difficult to characterize due to limitation of our system sizes. We believe all n-tangles are maximized near critical point. We need to study larger system sizes in order to better study the critical region and extract the critical exponents. (e. g. DMRG, finite-size scaling)

References o o o Caslav Brukner, and Anton Zeilinger. "Operationally Invariant Quantum Information" Phys. Rev. Lett. 83, 3354 (1999). Jian-Ming Cai 1, Zheng-Wei Zhou 1, and Xing-Xiang Zhou 2, and Guang-Can, "Information-Theoretic Measure of Genuine Multi. Qubit Entanglement" Phys. Rev. A 74, 042338 (2006). T. J. Osborne, and M. A. Nielsen, "Entanglement in a simple quantum phase transition" Phys. Rev. A 66, 032110 (2002).

Thank you
- Slides: 22