Multiprocessor synchronization algorithms 20225241 LocalSpin Algorithms Lecturer Danny

Multiprocessor synchronization algorithms (20225241) Local-Spin Algorithms Lecturer: Danny Hendler This presentation is based on the book “Synchronization Algorithms and Concurrent Programming” by G. Taubenfeld and on a the survey “Shared-memory mutual exclusion: major research trends since 1986” by J. Anderson, Y-J. Kim and T. Herman

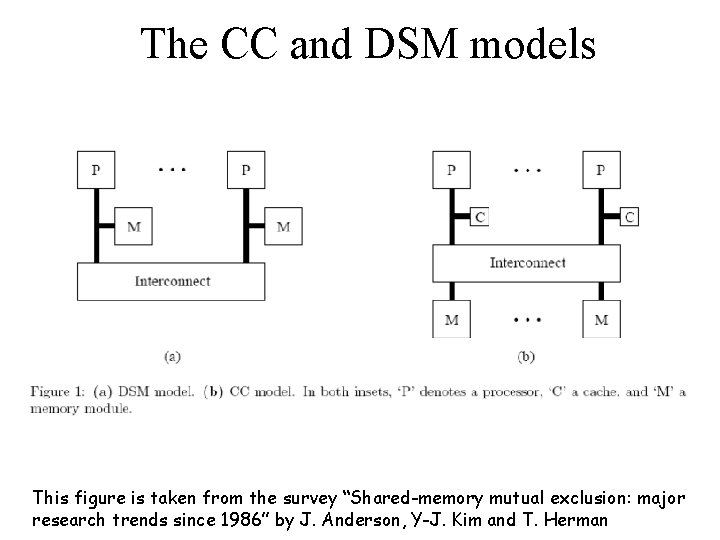
The CC and DSM models This figure is taken from the survey “Shared-memory mutual exclusion: major research trends since 1986” by J. Anderson, Y-J. Kim and T. Herman

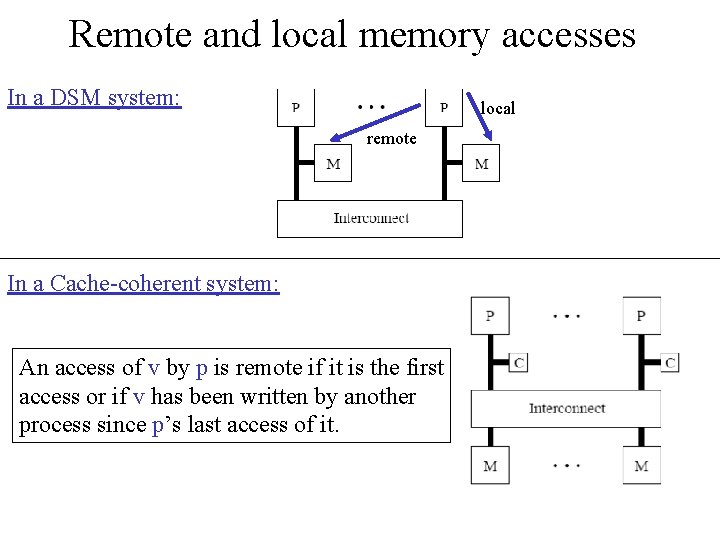
Remote and local memory accesses In a DSM system: local remote In a Cache-coherent system: An access of v by p is remote if it is the first access or if v has been written by another process since p’s last access of it.

Local-spin algorithms In a local-spin algorithm, all busy waiting (‘await’) is done by read-only loops of local-accesses, that do not cause interconnect traffic. The same algorithm may be local-spin on one architecture (DSM/CC) and non-local spin on the other! For local-spin algorithms, our complexity metric is the worst-case number of Remote Memory References (RMRs)

Peterson’s 2 -process algorithm Program for process 0 Program for process 1 1. 2. 3. 4. 5. b[0]: =true turn: =0 await (b[1]=false or turn=1) CS b[1]: =false b[1]: =true turn: =1 await (b[0]=false or turn=0) CS b[1]: =false Is this algorithm local-spin on a DSM machine? Is this algorithm local-spin on a CC machine? No Yes

Peterson’s 2 -process algorithm Program for process 0 Program for process 1 1. 2. 3. 4. 5. b[0]: =true turn: =0 await (b[1]=false or turn=1) CS b[0]: =false b[1]: =true turn: =1 await (b[0]=false or turn=0) CS b[1]: =false What is the RMR complexity on a DSM machine? Unbounded What is the RMR complexity on a CC machine? Constant

Kessel’s single-writer algorithm Program for process 0 Program for process 1 1. 2. 3. 4. 5. 6. b[0]: =true local[0]: =turn[1] turn[0]: =local[0] Await (b[1]=false or local[0]<>turn[1]) CS b[0]: =false 5. 6. b[1]: =true local[1]: =1 -turn[0] turn[1]: =local[1] Await (b[0]=false or local[1]=turn[0]) CS b[1]: =false Can Kessel’s algorithm be made local-spin on a DSM machine? Yes, if: q b[1], turn[1] are located at p 0’s memory module q b[0], turn[0] are located at p 1’s memory module

Local Spinning Mutual Exclusion Using Strong Primitives

Anderson’s queue-based algorithm Shared: integer ticket – A RMW object, initially 0 bit valid[0. . n-1], initially valid[0]=1 and valid[i]=0, for i {1, . . , n-1} Local: integer my. Ticket valid ticket 0 1 2 3 n-1 1 0 0 Program for process i 1. 2. 3. 4. 5. my. Ticket=fetch-and-inc-modulo-n(ticket) ; take a ticket await valid[my. Ticket]=1 ; wait for your turn CS valid[my. Ticket]: =0 ; dequeue valid[my. Ticket+1 mod n]: =1 ; signal successor

Anderson’s queue-based algorithm (cont’d) After entry section of p 3 Initial configuration my. Ticket 3 ticket 0 valid 1 0 0 ticket 1 valid 1 0 0 After p 1 performs entry section ticket 2 valid 1 my. Ticket 3 my. Ticket 1 0 0 0 0 After p 3 exits my. Ticket 1 ticket 2 valid 0 1 0 0

Anderson’s queue-based algorithm (cont’d) Program for process i 1. 2. 3. 4. 5. my. Ticket=fetch-and-inc-modulo-n(ticket) ; take a ticket await valid[my. Ticket]=1 ; wait for your turn CS valid[my. Ticket]: =0 ; dequeue valid[my. Ticket+1 mod n]: =1 ; signal successor What is the RMR complexity on a DSM machine? Unbounded What is the RMR complexity on a CC machine? Constant

Graunke and Thakkar’s algorithm Uses the more common swap primitive: swap(w, new) do atomically prev: =w w: =new return prev

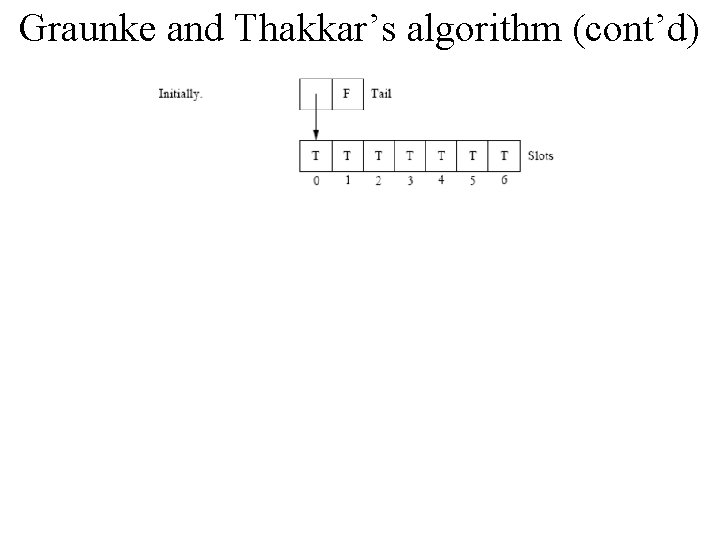
Graunke and Thakkar’s algorithm (cont’d) Shared: bit slots[0. . n-1], initially slots[i]=1, for i {0, . . , n-1} structure {bit value, bit *node} tail, initially {0, &slots[0]} Local: structure {bit value, bit *node} my. Record, prev bit temp tail 0 0 1 2 3 n-1 1 1 slots

Graunke and Thakkar’s algorithm (cont’d) Shared: bit slots[0. . n-1], initially slots[i]=1, for i {0, . . , n-1} structure {bit value, bit* slot} tail, initially {0, &slot[0]} Local: structure {bit value, bit* node} my. Record, prev, bit temp Program for process i 1. 2. 3. 4. 5. 6. 7. my. Record. value: =slots[i] ; prepare to thread yourself to queue my. Record. slot: =&slots[i] prev=swap(&tail, my. Record) ; prev now points to predecessor await (*prev. slot ≠prev. value) ; local spin until predecessor’s value changes CS temp: =1 -slots[i]: =temp ; signal successor

Graunke and Thakkar’s algorithm (cont’d)

Graunke and Thakkar’s algorithm (cont’d) Program for process i 1. 2. 3. 4. 5. 6. 7. my. Record. value: =slots[i] ; prepare to thread yourself to queue my. Record. slot: =&slots[i] prev=swap(&tail, my. Record) ; prev now points to predecessor await (*prev. slot ≠prev. value) ; local spin until predecessor’s value changes CS temp: =1 -slots[i]: =temp ; signal successor What is the RMR complexity on a DSM machine? Unbounded What is the RMR complexity on a CC machine? Constant

The MCS queue-based algorithm Has constant RMR complexity under both the DSM and CC models Uses swap and CAS Type: Qnode: structure {bit locked, Qnode *next} Shared: Qnodes[0. . n-1] Qnode *tail initially nil Local: Qnode *my. Node, initially &nodes[i] Qnode *prev, *successor

The MCS queue-based algorithm (cont’d) Program for process i 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. my. Node. next : = nil ; prepare to be last in queue prev : = my. Node ; prepare to thread yourself swap(&tail, prev) ; tail now points to my. Node if (prev ≠ nil) ; I need to wait for a predecessor *my. Node. locked : = true ; prepare to wait *prev. next : = my. Node ; let my predecessor know it has to unlock me await my. Node. locked : = false CS if (my. Node. next = nil) ; if not sure there is a successor if (compare-and-swap(tail, my. Node, nil) = false) ; if there is a successor await (my. Node->next ≠ null) ; spin until successor let me know its identity successor : = my. Node->next ; get a pointer to my successor->locked : = false ; unlock my successor else ; for sure, I have a successor : = my. Node->next ; get a pointer to my successor->locked : = false ; unlock my successor

The MCS queue-based algorithm (cont’d)

Local Spinning Mutual Exclusion Using reads and writes

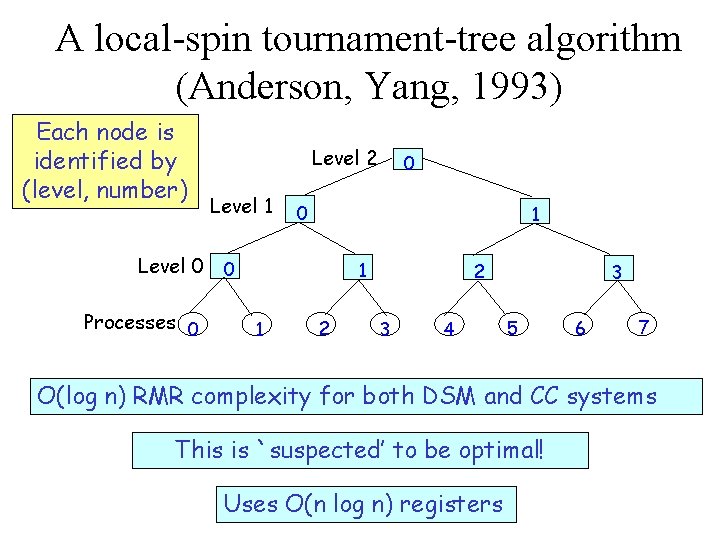
A local-spin tournament-tree algorithm (Anderson, Yang, 1993) Each node is identified by (level, number) Level 2 Level 1 0 1 Level 0 0 Processes 0 0 1 1 2 2 3 4 3 5 6 7 O(log n) RMR complexity for both DSM and CC systems This is `suspected’ to be optimal! Uses O(n log n) registers

A local-spin tournament-tree algorithm (cont’d) Shared: - Per each node, v, there are 3 registers: name[level, 2 node], name[level, 2 node+1] initially -1 turn[level, node] - Per each level l and process i, a spin flag: flag[level, i] Local: level, node, id

A local-spin tournament-tree algorithm (cont’d) Program for process i 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. id: =i For level = o to log n-1 do ; from leaf to root node: = id/2 ; the current node name[level, 2 node+(id mod 2)]: =i ; identify yourself turn[level, node]: =id ; update the tie-breaker flag[level, i]: =0 ; initialize the locally-accessible spin flag if (even(id)) rival: =name[level, id+1] else rival: =name[level, id-1] if ( (rival ≠ -1) and (turn[level, node] = i) ) ; if not sure I should precede rival if (flag[level, rival] =0) flag[level, rival]: =1 ; release the rival from waiting await flag[level, i] ≠ 0 ; await until sure the rival updated the tie-breaker if (turn[level, node]=i) ; if I lost await flag[level, i]=2 ; wait till rival notifies me its my turn id: =node ; move to the next level CS for level=log n – 1 downto 0 do ; begin exit code id: = i/2 level , node: = id/2 ; set node and id name[level, 2 node+(id mod 2]) : =-1 ; erase name rival : = turn[level, node] ; find who rival is (if there is one) if rival ≠ i ; if there is a rival flag[level, rival] : =2 ; notify rival