MULTIPLYING TWO MATRICES The product of two matrices

MULTIPLYING TWO MATRICES The product of two matrices A and B is defined provided the number of columns in A is equal to the number of rows in B.

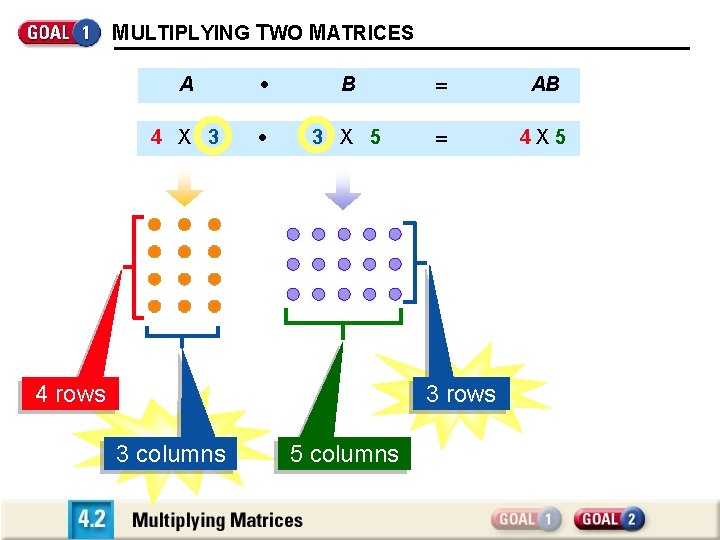
MULTIPLYING TWO MATRICES A B AB 4 X 3 3 X 5 4 rows 3 columns 5 columns

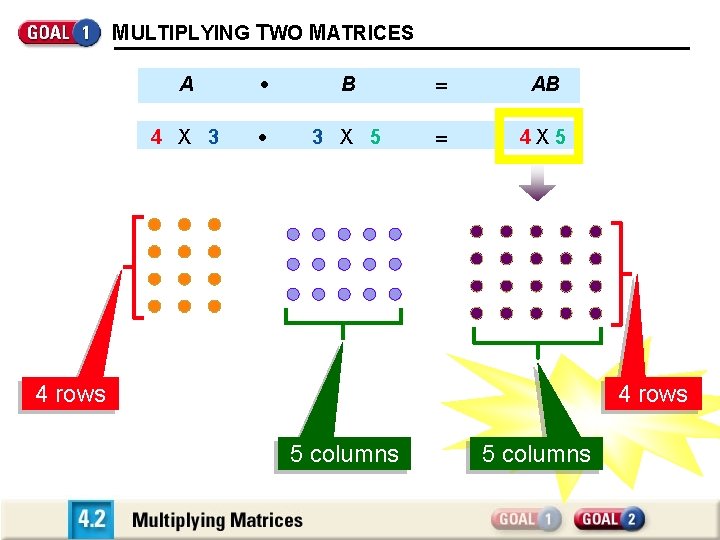
MULTIPLYING TWO MATRICES A B AB 4 X 3 3 X 5 4 rows 5 columns

MULTIPLYING TWO MATRICES If A is a 4 X 3 matrix and B is a 3 X 5 matrix, then the product AB is a 4 X 5 matrix.

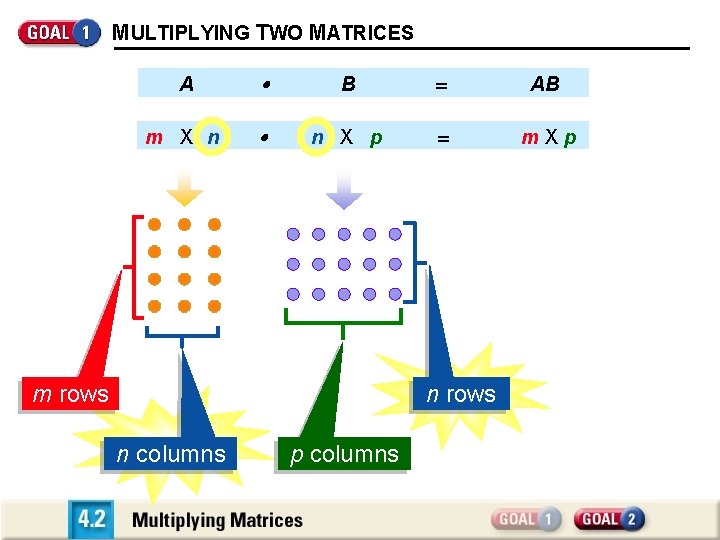
MULTIPLYING TWO MATRICES A B AB m X n n X p m. Xp m rows n columns p columns

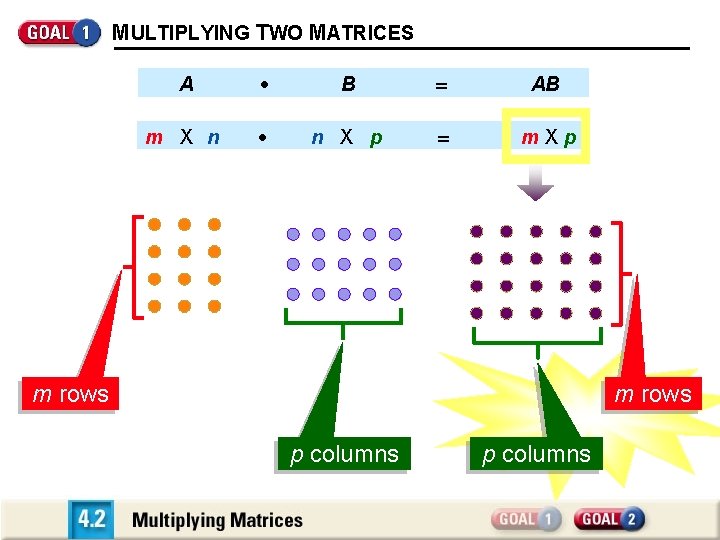
MULTIPLYING TWO MATRICES A B AB m X n n X p m. Xp m rows p columns

MULTIPLYING TWO MATRICES If A is an m X n matrix and B is an n X p matrix, then the product AB is an m X p matrix.

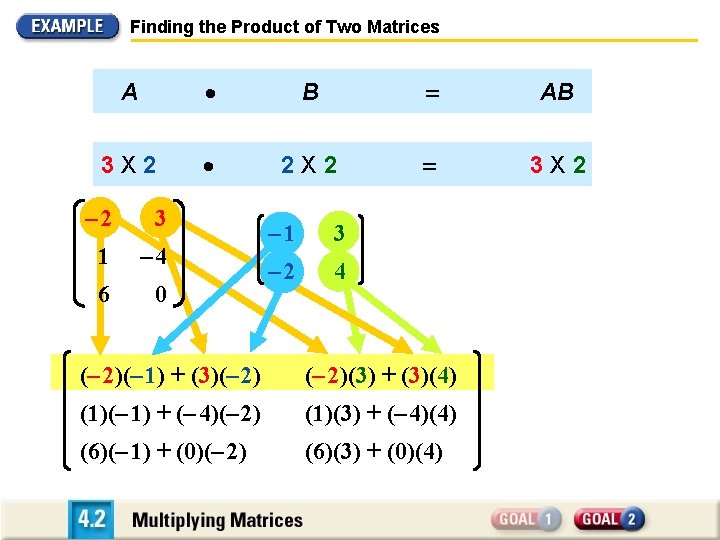
Finding the Product of Two Matrices Find AB if – 2 3 A = 1 – 4 6 0 and B= – 1 – 2 3 4 SOLUTION Because A is a 3 X 2 matrix and B is a 2 X 2 matrix, the product AB is defined and is a 3 X 2 matrix. To write the entry in the first row and first column of AB, multiply corresponding entries in the first row of A and the first column of B. Then add. Use a similar procedure to write the other entries of the product.

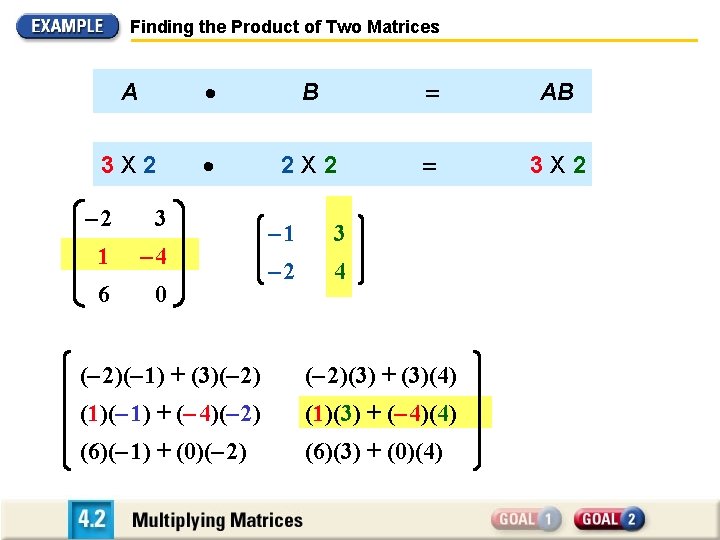
Finding the Product of Two Matrices A B AB 3 X 2 2 X 2 3 X 2 – 2 3 1 – 4 6 0 – 1 3 – 2 4 (– 2)(– 1) + (3)(– 2)(3) + (3)(4) (1)(– 1) + (– 4)(– 2) (1)(3) + (– 4)(4) (6)(– 1) + (0)(– 2) (6)(3) + (0)(4)

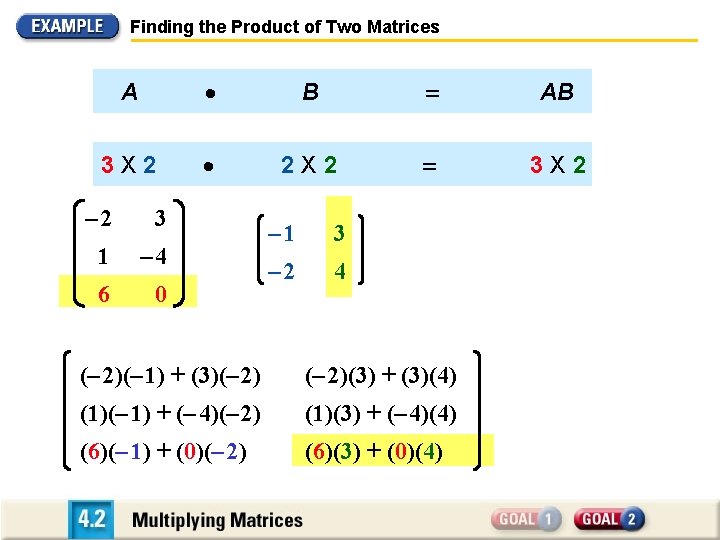
Finding the Product of Two Matrices A B AB 3 X 2 2 X 2 3 X 2 – 2 3 1 – 4 6 0 – 1 3 – 2 4 (– 2)(– 1) + (3)(– 2)(3) + (3)(4) (1)(– 1) + (– 4)(– 2) (1)(3) + (– 4)(4) (6)(– 1) + (0)(– 2) (6)(3) + (0)(4)

Finding the Product of Two Matrices A B AB 3 X 2 2 X 2 3 X 2 – 2 3 1 – 4 6 0 – 1 3 – 2 4 (– 2)(– 1) + (3)(– 2)(3) + (3)(4) (1)(– 1) + (– 4)(– 2) (1)(3) + (– 4)(4) (6)(– 1) + (0)(– 2) (6)(3) + (0)(4)

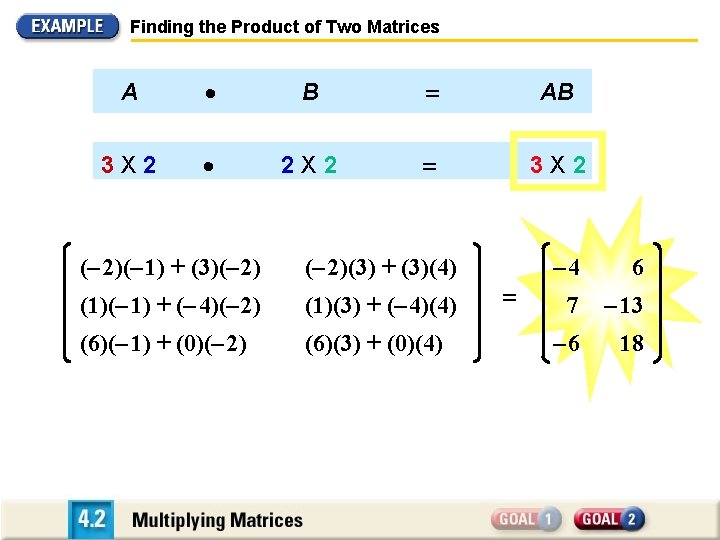
Finding the Product of Two Matrices A B AB 3 X 2 2 X 2 3 X 2 (– 2)(– 1) + (3)(– 2)(3) + (3)(4) (1)(– 1) + (– 4)(– 2) (1)(3) + (– 4)(4) (6)(– 1) + (0)(– 2) (6)(3) + (0)(4) – 4 6 7 – 13 – 6 18

MULTIPLYING TWO MATRICES Matrix multiplication is not, in general, commutative. CONCEPT SUMMARY PROPERTIES OF MATRIX MULTIPLICATION Let A, B, and C be matrices and let g be a scalar. ASSOCIATIVE PROPERTY OF MATRIX MULTIPLICATION A(BC ) = (AB )C LEFT DISTRIBUTIVE PROPERTY A(B + C ) = AB + AC RIGHT DISTRIBUTIVE PROPERTY (A + B )C = AC + BC ASSOCIATIVE PROPERTY OF SCALAR MULTIPLICATION g (AB ) = (g. A )B = A(g. B )

USING MATRIX MULTIPLICATION IN REAL LIFE Matrix multiplication is useful in business applications because an inventory matrix, when multiplied by a cost per item matrix, results in total cost matrix. Inventory matrix m. Xn • Cost per item matrix n. Xp = Total cost matrix m. Xp For the total cost matrix to be meaningful, the column labels for the inventory matrix must match the row labels for the cost per item matrix.

Using Matrices to Calculate the Total Cost SPORTS Two softball teams submit equipment lists for the season. Each bat costs $21, each ball costs $4, and each uniform costs $30. Use matrix multiplication to find the total cost of equipment for each team.

Using Matrices to Calculate the Total Cost SOLUTION Write the equipment lists and costs per item in matrix form. Use matrix multiplication to find the total cost. Set up matrices so that columns of the equipment matrix match rows of the cost matrix. COST EQUIPMENT Bats Women’s team Men’s team 12 15 Dollars Balls Uniforms 45 38 15 17 Bats Balls Uniforms 21 4 30

Using Matrices to Calculate the Total Cost Total equipment cost for each team can be obtained by multiplying the equipment matrix by the cost per item matrix. The equipment matrix is 2 X 3 and the cost per item matrix is 3 X 1. Their product is a 2 X 1 matrix. 12 45 15 15 38 17 21 4 30 = 12(21) + 45(4) + 15(30) 15(21) + 38(4) + 17(30) = 882 977

Using Matrices to Calculate the Total Cost TOTAL COST Dollars The labels of the product are: Women’s team Men’s team 882 977 The total cost of equipment for the women’s team is $882, and the total cost of equipment for the men’s team is $977.