MULTIPLICATION USING HISTORICAL METHODSJoanne Peeples El Paso Community

Increasingly students are entering college unable to multiply or divide integers without using a

MULTIPLICATION 26 X 4 ___26______ Add: 64 1 4 2 8 4 16 8

DIVISION (NO REMAINDER) 161 7 _____161___ 1 2 4 8 16 32 161 =

DIVISION (WITH REMAINDER) 84 11 _____84___ 1 11 2 22 4 44 8 88

FRACTIONS DECREASE IN SIZE (SO THEY CAN BE USED FOR ESTIMATION. ) In a

FRACTIONS MUST NOT BE “CLOSE” TO EACH OTHER.

A FRACTIONAL REPRESENTATION MAY NOT BE UNIQUE.

AND AS YOU MAY HAVE SEEN, ALL THE FRACTIONS ARE UNIT FRACTIONS.

HOW DO YOU FIND A FRACTIONAL REPRESENTATION?

WHAT IF THE AREA OF A TRIANGLE WHOSE BASE IS 37 UNITS AND HEIGHT

MULTIPLICATION PER GELOSIA 2, 314 X 157 = 363, 298 2 0 3 0

BIBLIOGRAPHY Reimer, David, Count Like an Egyptian, A Hands on Introduction to Ancient Mathematics.

THANK YOU! jpeeples. @epcc. edu Power. Point Artist – Amie Stoker

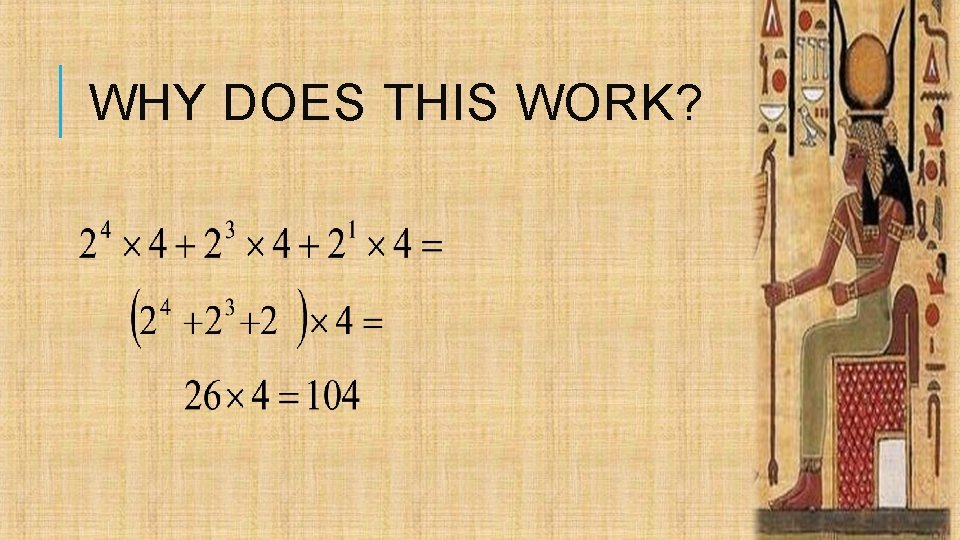
Slides: 28

Download presentation

MULTIPLICATION USING HISTORICAL METHODSJoanne Peeples El Paso Community College jpeeples@epcc. edu

Increasingly students are entering college unable to multiply or divide integers without using a calculator (hence having little number sense). Rather than repeat multiplication methods they have learned, why not try Egyptian arithmetic, multiplication per gelosia (“by jealousy”) or Napier’s bones? History plus math is often a winning strategy.

EGYPTIAN NUMBERS

MULTIPLICATION 26 X 4 ___26______ Add: 64 1 4 2 8 4 16 8 32 16 64 32 128 Too Big! 32 is bigger than 26 26 = 16 + 10 = 16 + 8 + 2 + 32 + 8 = 104

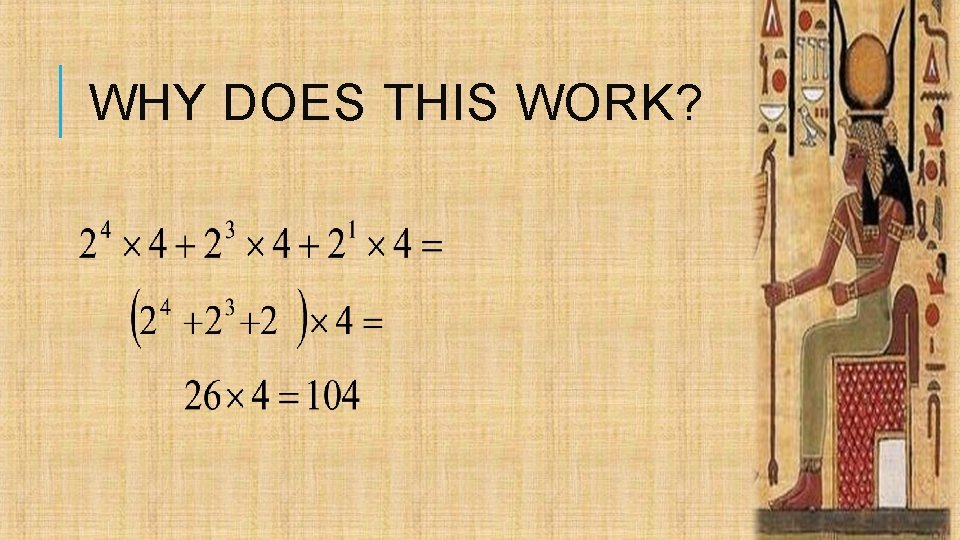
WHY DOES THIS WORK?

DIVISION (NO REMAINDER) 161 7 _____161___ 1 2 4 8 16 32 161 = 112 + 28 + 14 + 7 Therefore 161 7 = 16 +4+2+1 = 23 7 14 28 56 112 224 Too Big! 224 is bigger than 161

DIVISION (WITH REMAINDER) 84 11 _____84___ 1 11 2 22 4 44 8 88 84 = 44 + 22 + 11 + 7 Therefore 84 11 = 4 + 2 + 1 = 7 with a remainder of 7 We would write 84 11 = 7 + 7/11 Too Big! 88 is bigger than 84

EGYPTIAN FRACTIONS │││ ∩│││││

EXAMPLE

FRACTIONS DECREASE IN SIZE (SO THEY CAN BE USED FOR ESTIMATION. ) In a sense, Egyptian fractions are closer to “our” decimal system than “our” fractions.

FRACTIONS NEVER REPEAT.

FRACTIONS MUST NOT BE “CLOSE” TO EACH OTHER.

A FRACTIONAL REPRESENTATION MAY NOT BE UNIQUE.

AND AS YOU MAY HAVE SEEN, ALL THE FRACTIONS ARE UNIT FRACTIONS.

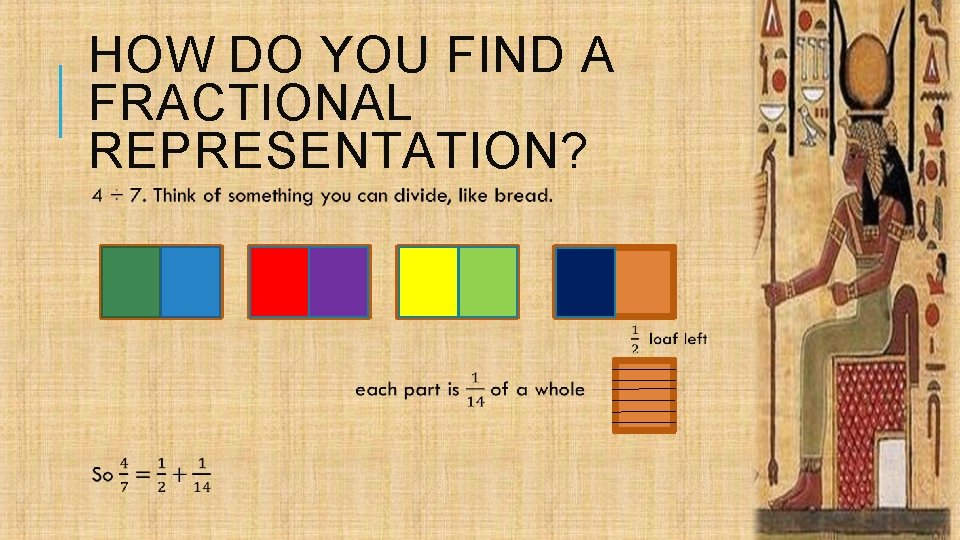
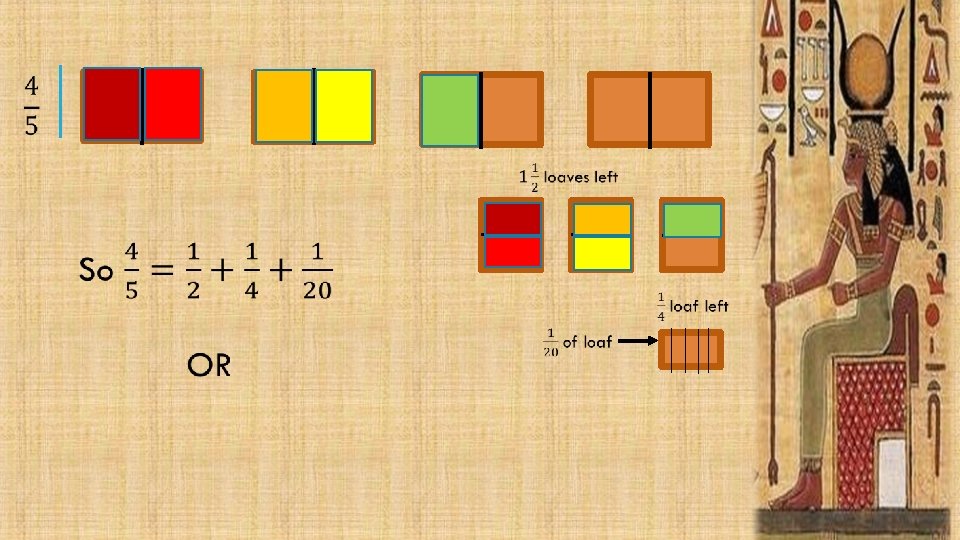
HOW DO YOU FIND A FRACTIONAL REPRESENTATION?

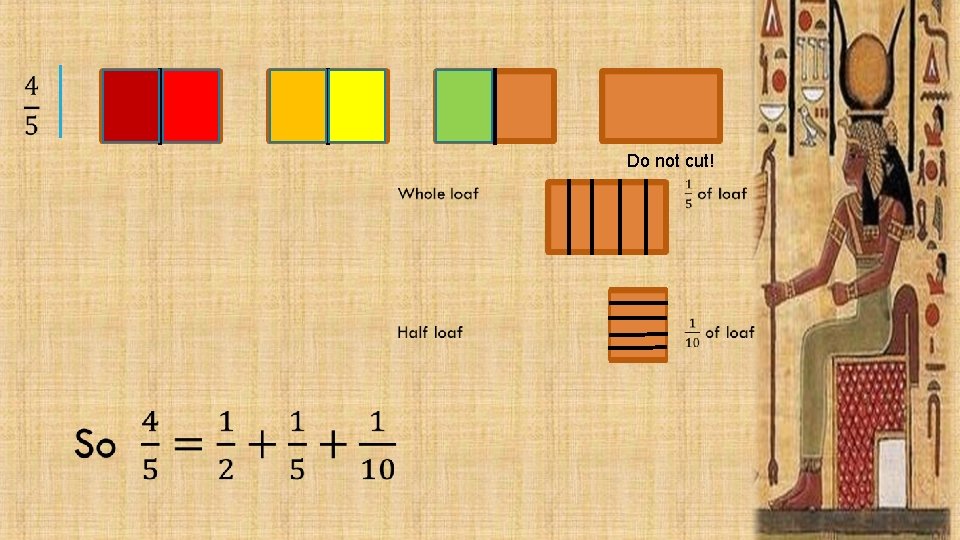
Do not cut!

WHAT IF THE AREA OF A TRIANGLE WHOSE BASE IS 37 UNITS AND HEIGHT IS 12 UNITS? (Write 1 37 = 20 + 16 + 1 10 + 8 + = 18 ││ as )

18 1 12 2 24 4 48 8 96 16 192 6 Area of triangle is 24 + 192 + 6 = 222 sq. units.

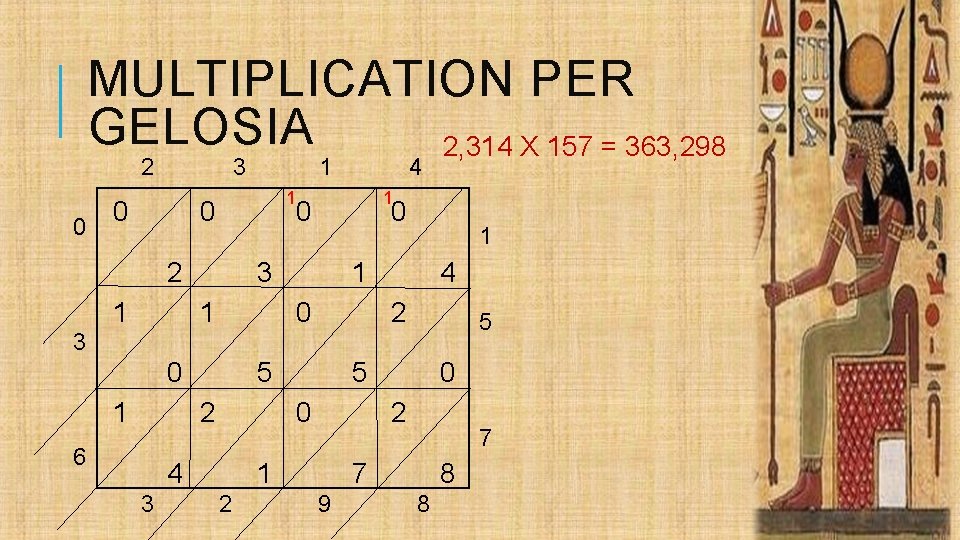
MULTIPLICATION PER GELOSIA 2, 314 X 157 = 363, 298 2 0 3 0 1 1 0 2 1 4 0 3 1 1 1 0 4 2 5 3 0 1 5 2 6 0 4 3 5 2 1 2 0 7 7 9 8 8

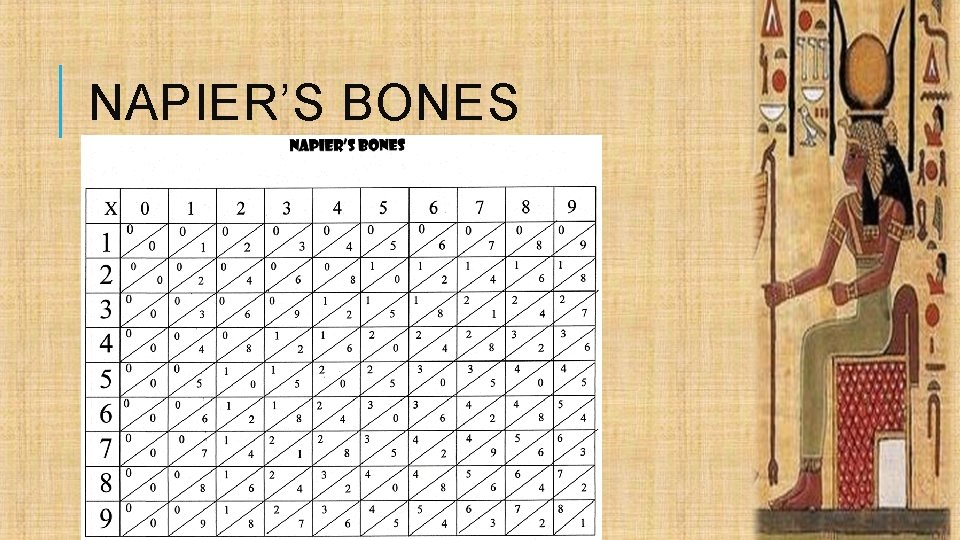
NAPIER’S BONES

BIBLIOGRAPHY Reimer, David, Count Like an Egyptian, A Hands on Introduction to Ancient Mathematics. Published by the Princeton University Press, 2014. Ifrah, Georges, The Universal History of Numbers. Published by John Wiley and Sons, Inc. , 2000 Napier, John, Rabdology, translated by William Frank Richardson. Volume 15 in the Charles Babbage Institute Reprint Series for the History of Computing. Published by the Massachusetts Institute of Technology and Tomash Publishers, 1990

THANK YOU! jpeeples. @epcc. edu Power. Point Artist – Amie Stoker