Multiplication is not just adding It is related

• Multiplication is not just “adding”. It is related to adding but the image of just adding to solve multiplication problems breaks down once fractions and decimals are in play. • 3/5 x 6/8 0. 27 x 3. 45 • Multiplication involves a proportional growth that can move in 2 or even 3 directions. . . • Area models are far more flexible and robust, the factors are measures of side length

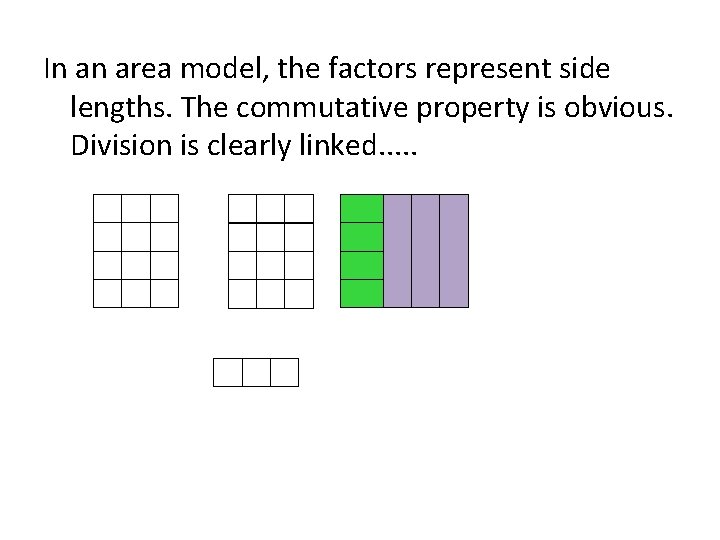
In an area model, the factors represent side lengths. The commutative property is obvious. Division is clearly linked. . .

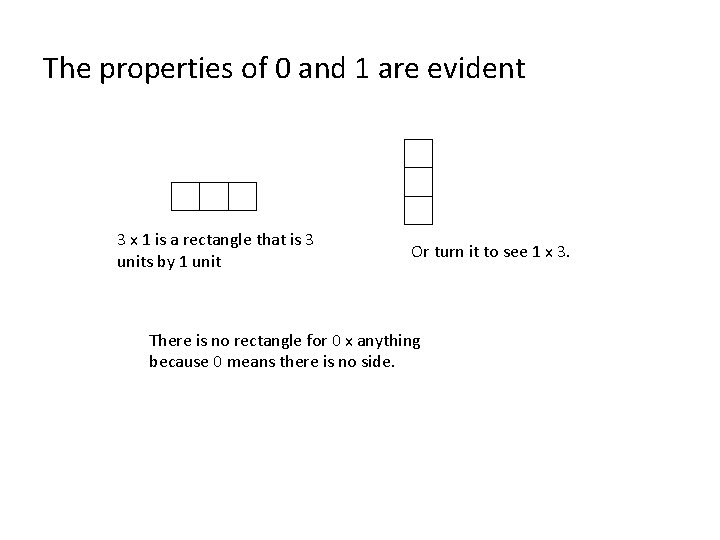
The properties of 0 and 1 are evident 3 x 1 is a rectangle that is 3 units by 1 unit Or turn it to see 1 x 3. There is no rectangle for 0 x anything because 0 means there is no side.

1 x 10 10 x 1 One of the reasons students struggle with place value. . . It is multiplicative but we teach it like adding. . . This is not a rod or a ten it is one unit of ten or ten units of one

This is not a “flat”. It covers an area of 10 by 10. It represents • (1 x 10) x 10 1 (100) • 1 (10 x 10) • 10 (10) 10 tens • 1 hundred • One hundred ones • 100(1)

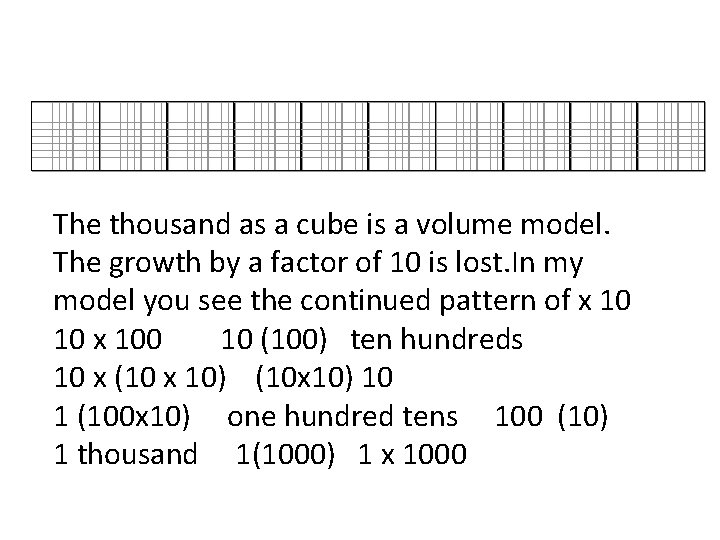
The thousand as a cube is a volume model. The growth by a factor of 10 is lost. In my model you see the continued pattern of x 10 10 x 100 10 (100) ten hundreds 10 x (10 x 10) (10 x 10) 10 1 (100 x 10) one hundred tens 100 (10) 1 thousand 1(1000) 1 x 1000

Cuisenaire rods focus attention on the growth by a unit. How can you use other rods to reason out why I am calling this the 3?

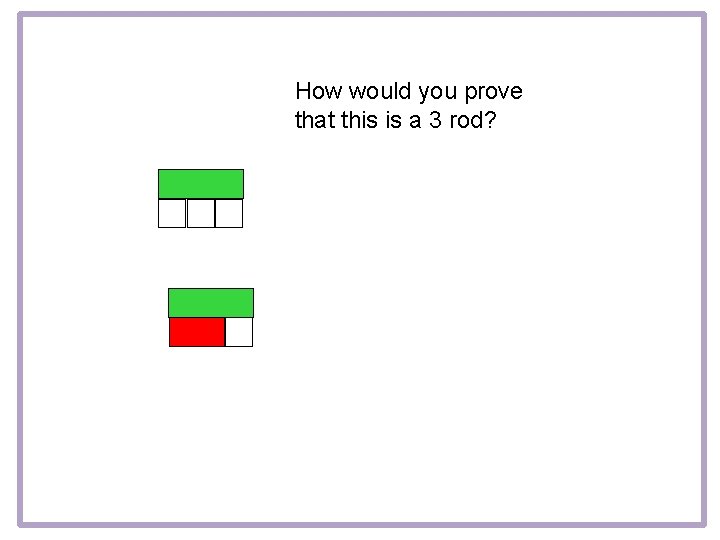
How would you prove that this is a 3 rod?

If this is 3 How much is this?

It is two units of 3 so (1 x 3)+(1 x 3) 2 (1 x 3) two one times threes or (3 x 1) + (3 x 1)

Explain this one:

(3 x 1) how many repetitions or “times”

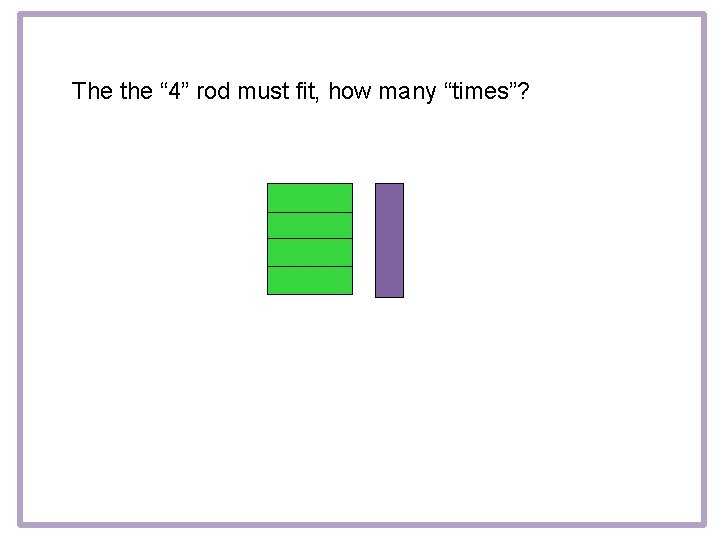
The the “ 4” rod must fit, how many “times”?

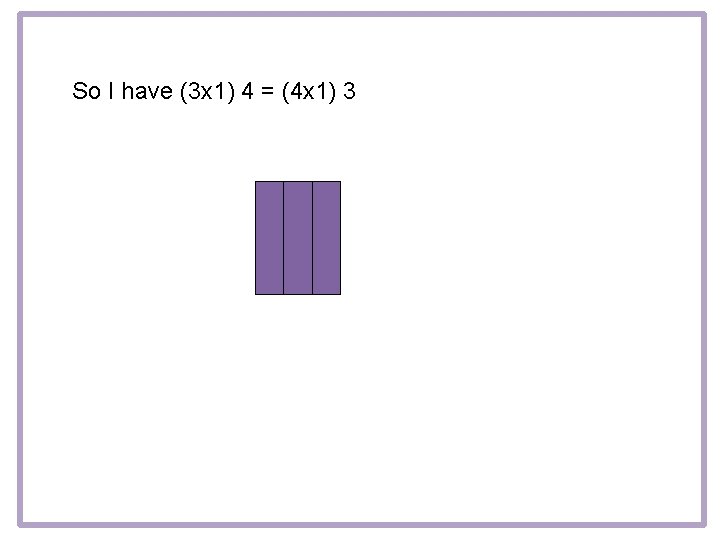
So I have (3 x 1) 4 = (4 x 1) 3

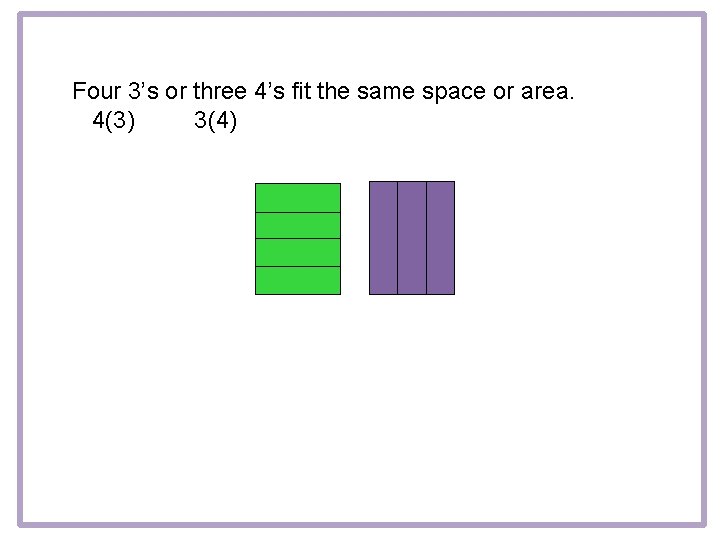
Four 3’s or three 4’s fit the same space or area. 4(3) 3(4)

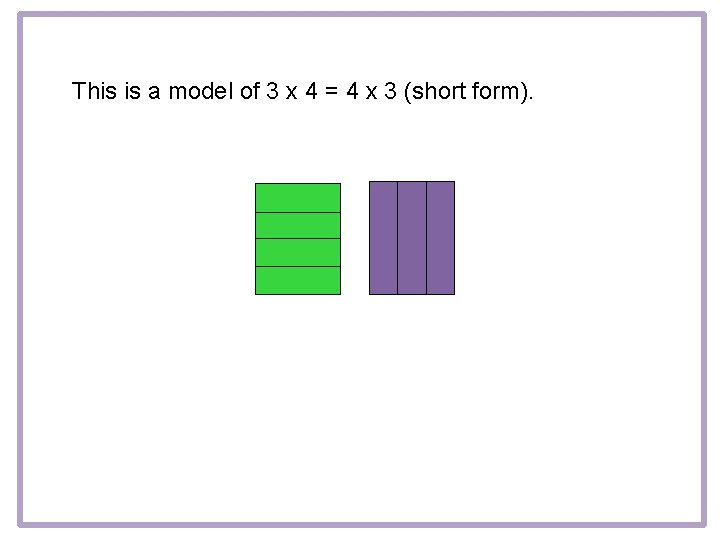
This is a model of 3 x 4 = 4 x 3 (short form).

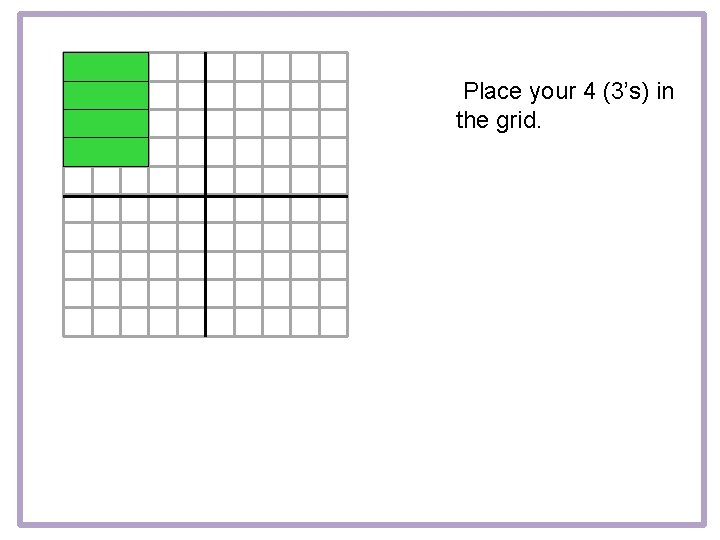
3 x 4 = 12 Place your 4 (3’s) in the grid.

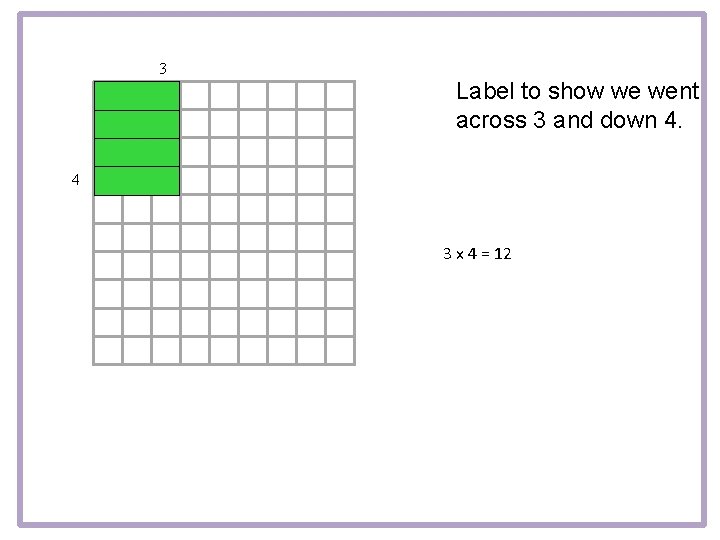
3 Label to show we went across 3 and down 4. 4 3 x 4 = 12

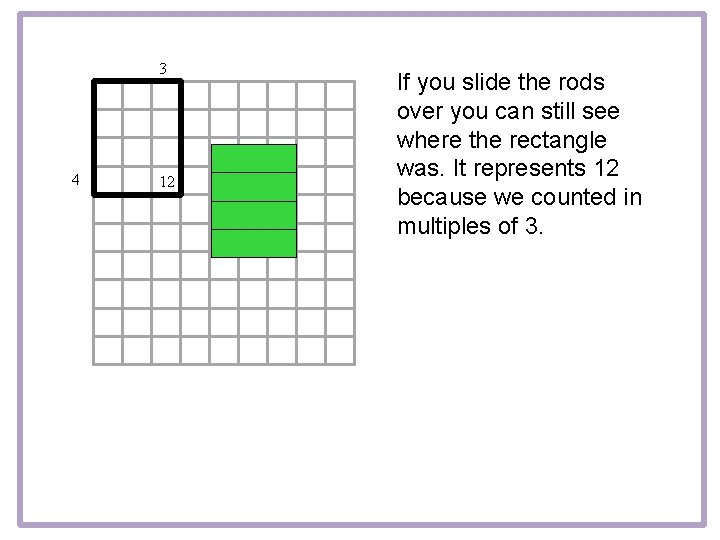
3 4 12 If you slide the rods over you can still see where the rectangle was. It represents 12 because we counted in multiples of 3.

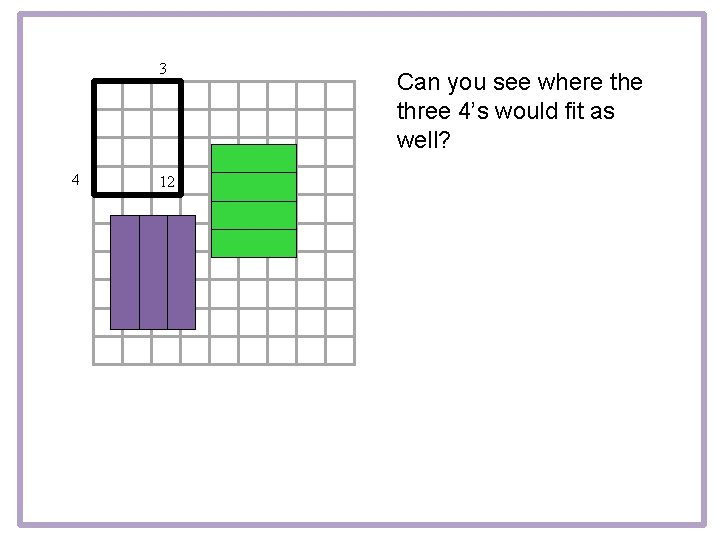
3 4 12 Can you see where three 4’s would fit as well?

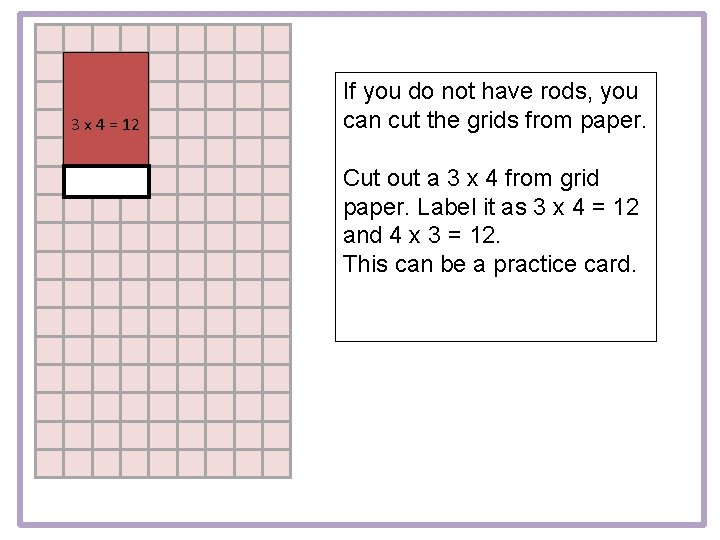
3 x 4 = 12 If you do not have rods, you can cut the grids from paper. Cut out a 3 x 4 from grid paper. Label it as 3 x 4 = 12 and 4 x 3 = 12. This can be a practice card.

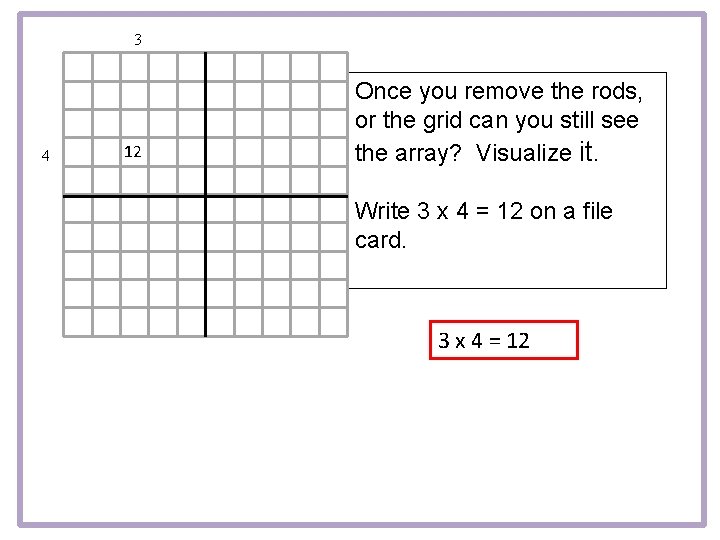
3 4 12 12 Once you remove the rods, or the grid can you still see the array? Visualize it. Write 3 x 4 = 12 on a file card. 3 x 4 = 12

3 What other facts can we build from this one? 4 12 12 You can turn it. . . Now you have 4 x 3 = 12. 3 x 4 = 12

3 3 4 4 2 12 What other facts can we build from this one? 12 12 You can turn it. . . Now you have 4 x 3 = 12. 3 x 4 = 12 4 x 3 = 12 4 x 3=3 x 4

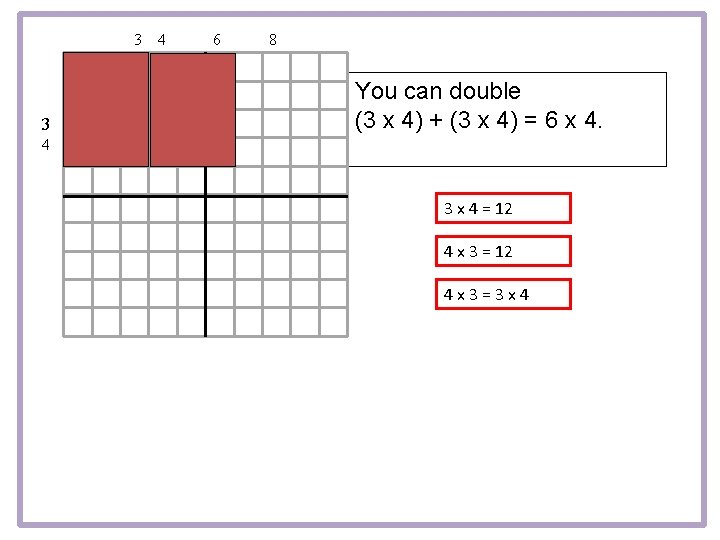
3 3 4 4 2 12 6 8 You can double (3 x 4) + (3 x 4) = 6 x 4. 12 12 3 x 4 = 12 4 x 3 = 12 4 x 3=3 x 4

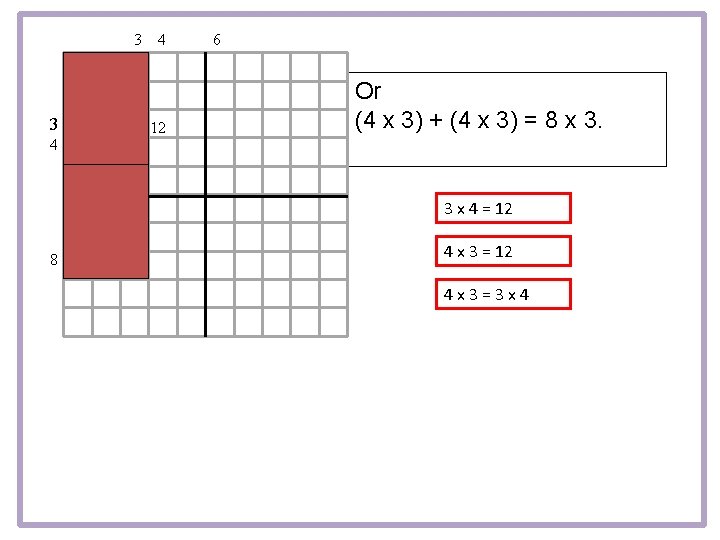
3 3 4 4 2 12 6 Or (4 x 3) + (4 x 3) = 8 x 3. 12 12 3 x 4 = 12 8 4 x 3 = 12 4 x 3=3 x 4

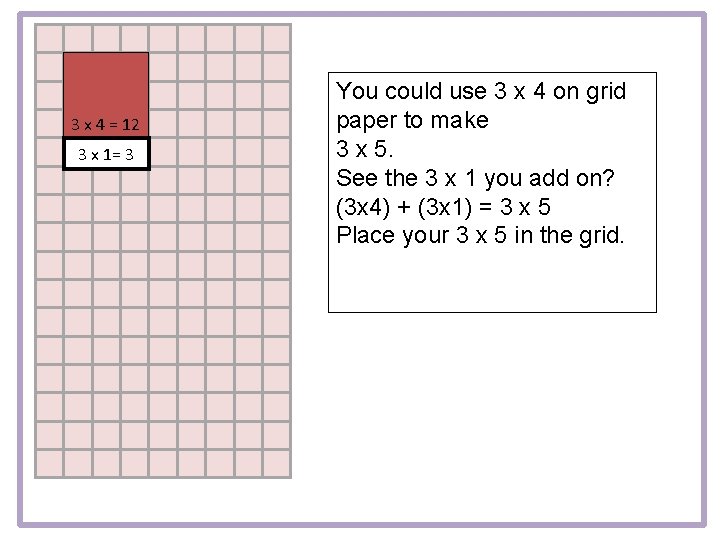
3 x 4 = 12 3 x 1= 3 You could use 3 x 4 on grid paper to make 3 x 5. See the 3 x 1 you add on? (3 x 4) + (3 x 1) = 3 x 5 Place your 3 x 5 in the grid.

Strategies for multiplication facts are built on the distributive property. Area models make strategies make sense. .

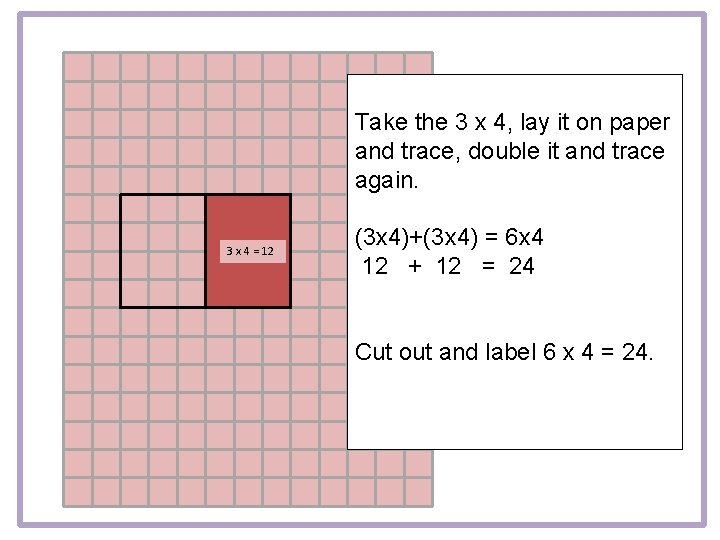
Take the 3 x 4, lay it on paper and trace, double it and trace again. 3 x 4 = 12 (3 x 4)+(3 x 4) = 6 x 4 12 + 12 = 24 Cut out and label 6 x 4 = 24.

Get out your 3 x 4 fact.

Get out your 3 x 5 fact.

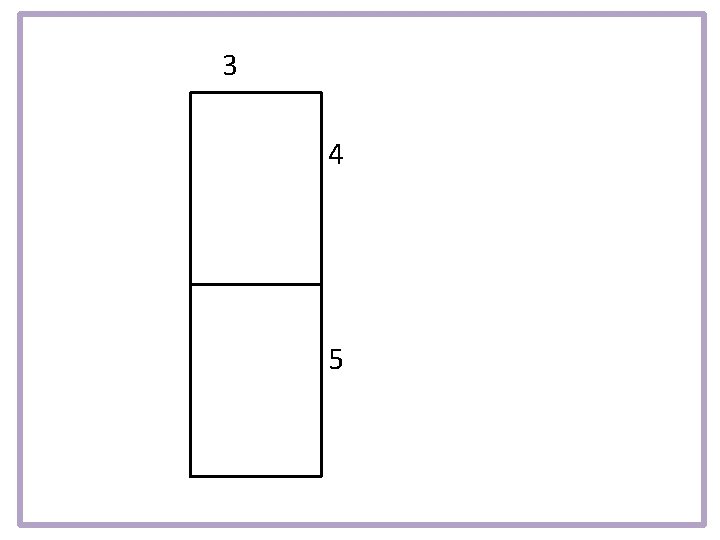
Add them together and sketch the rectangle they make. Label the rectangle.

3 4 5

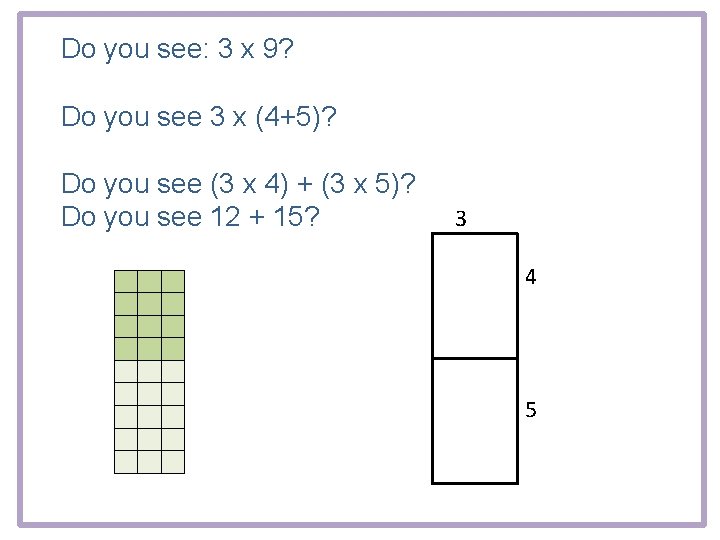
Do you see: 3 x 9? Do you see 3 x (4+5)? Do you see (3 x 4) + (3 x 5)? Do you see 12 + 15? 3 4 5

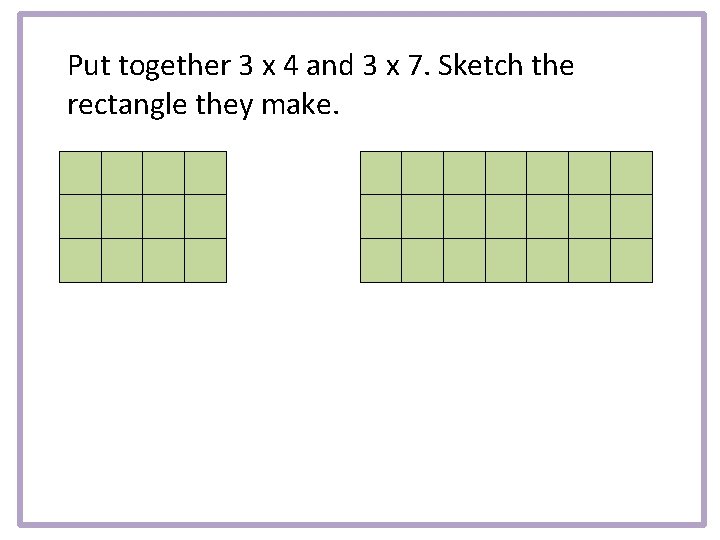
Put together 3 x 4 and 3 x 7. Sketch the rectangle they make.

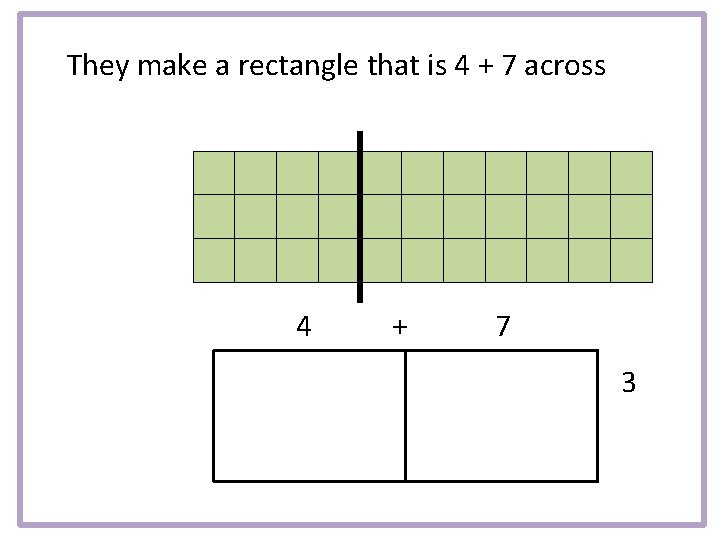
They make a rectangle that is 4 + 7 across 4 + 7 3

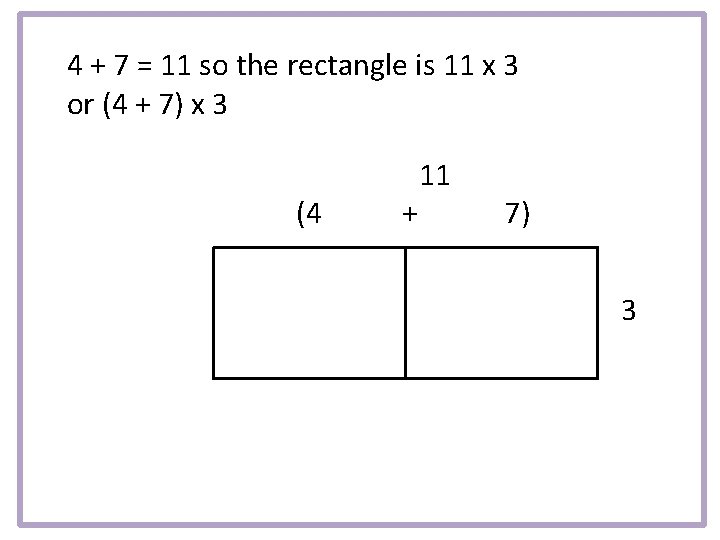
4 + 7 = 11 so the rectangle is 11 x 3 or (4 + 7) x 3 (4 + 11 7) 3

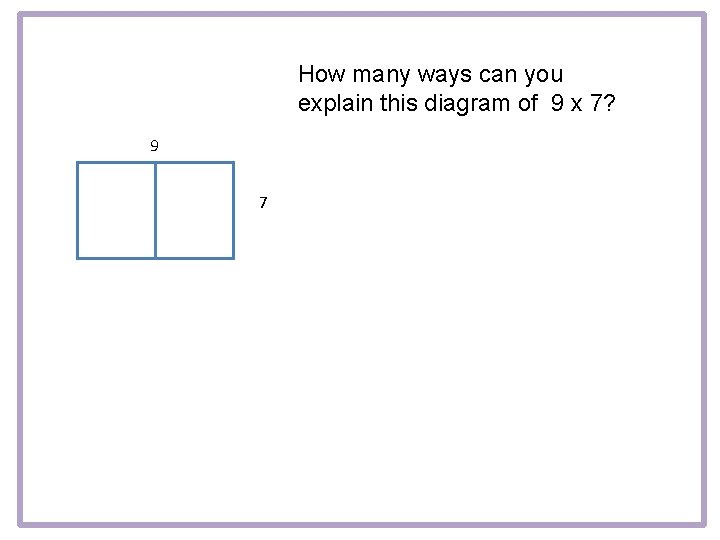
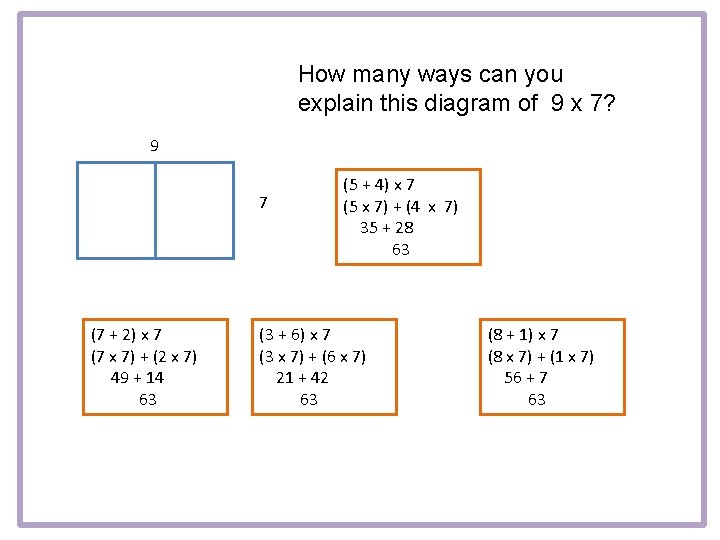
How many ways can you explain this diagram of 9 x 7? 9 7

How many ways can you explain this diagram of 9 x 7? 9 7 (7 + 2) x 7 (7 x 7) + (2 x 7) 49 + 14 63 (5 + 4) x 7 (5 x 7) + (4 x 7) 35 + 28 63 (3 + 6) x 7 (3 x 7) + (6 x 7) 21 + 42 63 (8 + 1) x 7 (8 x 7) + (1 x 7) 56 + 7 63

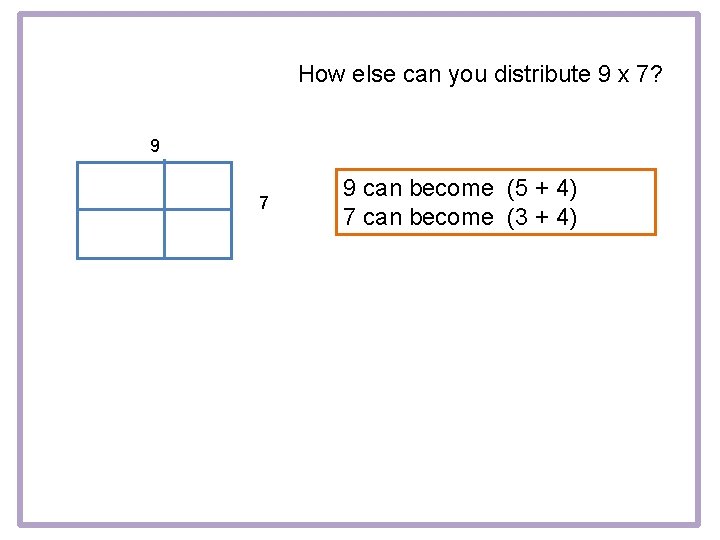
How else can you distribute 9 x 7? 9 7 9 x (? + ? )

How else can you distribute 9 x 7? 9 7 9 can become (? + ? ) 7 can become (? + ? )

How else can you distribute 9 x 7? 9 7 9 can become (5 + 4) 7 can become (3 + 4)

How else can you distribute 9 x 7? 5 +4 3 + 4 9 can become (5 + 4) 7 can become (3 + 4)

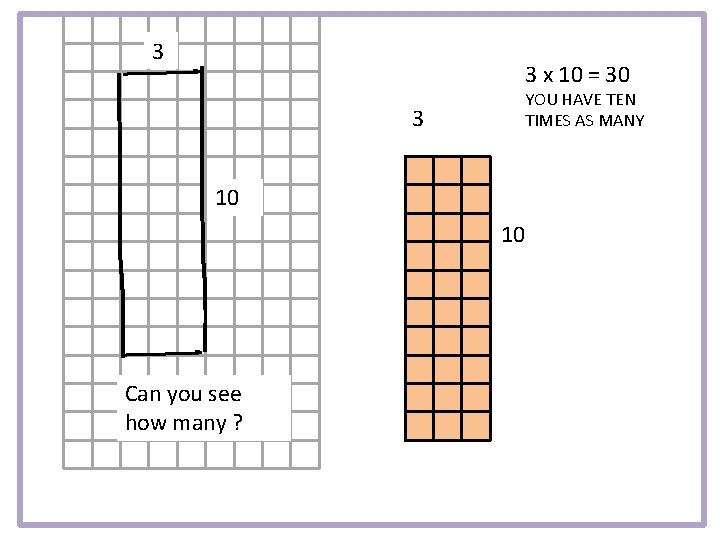
Multiplying by Ten: SCALING (TIMES AS MANY) Remember multiplication is modeled with equal groups pushed into rectangular arrays So think about what 3 x 10 would look like?

3 3 x 10 = 30 3 YOU HAVE TEN TIMES AS MANY 10 10 Can you see how many ?

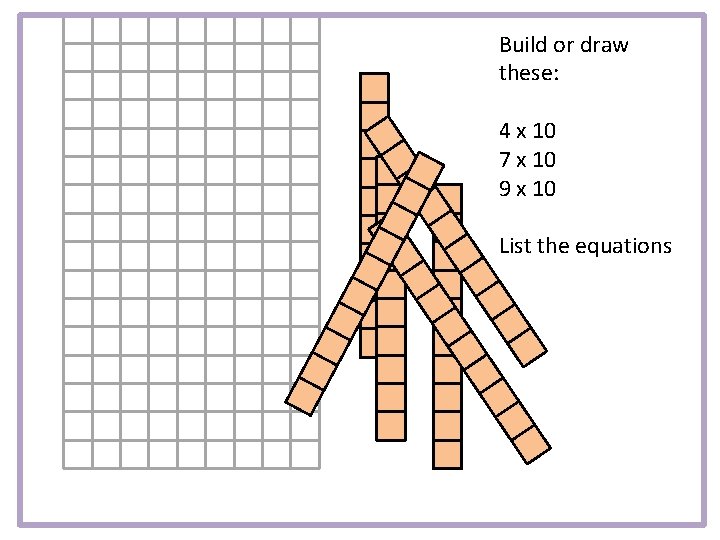
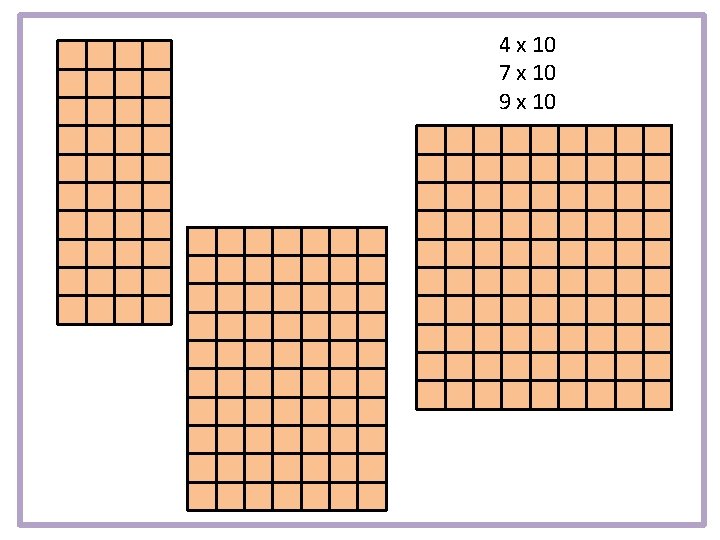
Build or draw these: 4 x 10 7 x 10 9 x 10 List the equations

4 x 10 7 x 10 9 x 10

3 x 10 = 30 4 x 10 = 40 7 x 10 = 70 9 x 10 = 90 Describe this next set without drawing: Can you see the growth in your head? 2 x 10 = 5 x 10 = 6 x 10 = 8 x 10 = Add them to your list.

3 x 10 = 30 4 x 10 = 40 5 x 10 = 50 6 x 10 = 60 7 x 10 = 70 9 x 10 = 90 What happens to the size of a number when you multiply by ten? What happens to the way you write a number when you multiply by ten?

Annexing zeroes means you increase the size of the number by ten times as many. The place value moves and zero takes the ones place. Each zero represents multiplying by ten.

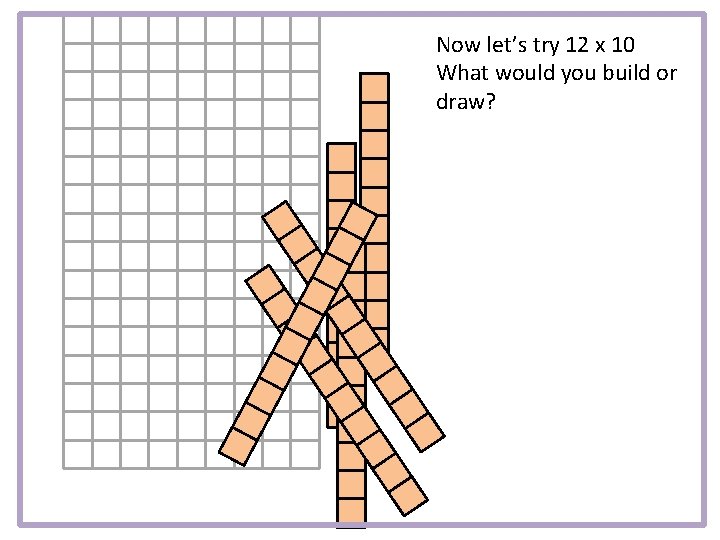
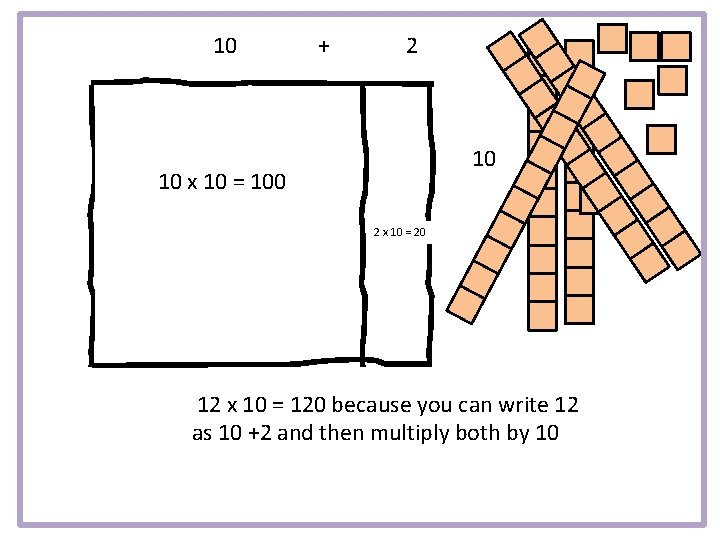
Now let’s try 12 x 10 What would you build or draw?

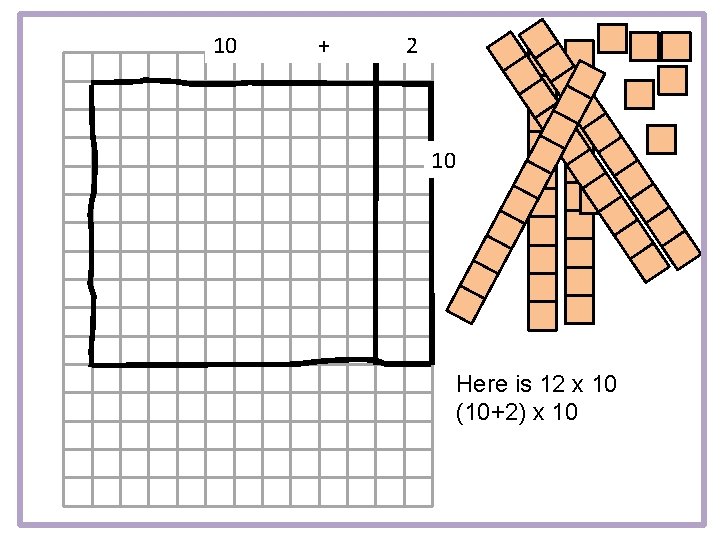
10 + 2 10 Here is 12 x 10 (10+2) x 10

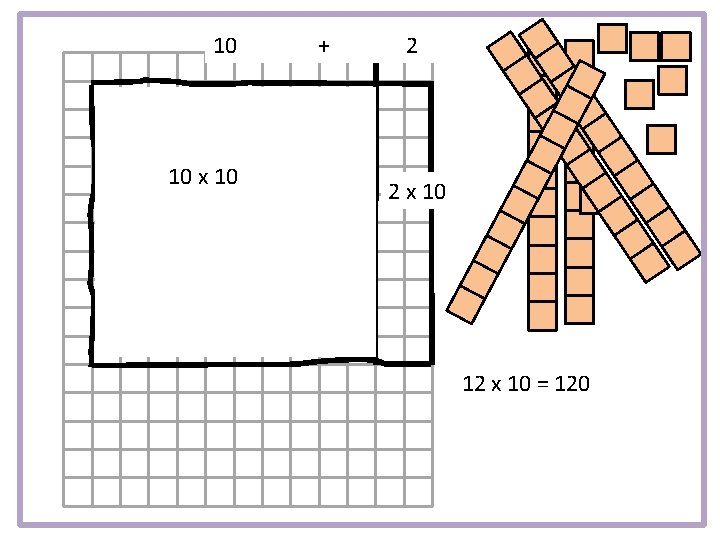
10 10 x 10 + 2 2 x 10 12 x 10 = 120

10 + 2 10 10 x 10 = 100 2 x 10 = 20 12 x 10 = 120 because you can write 12 as 10 +2 and then multiply both by 10

Once students have the area model as a distribution and are familiar with multiplying by ten, moving to double digit factors is just a bigger puzzle. If we have time. . Next ppt.