Multiplication Facts Using Strategies David Mc Killop Making

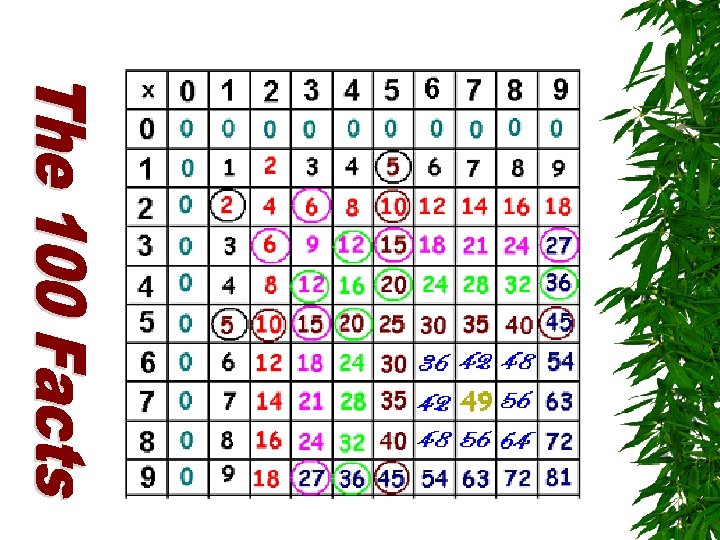
Multiplication Facts Using Strategies David Mc. Killop Making Math Matter, Inc.

Why should students learn the number facts? They are the basis of all mental math strategies, and mental math is the most widely used form of computation in everyday life Knowing facts is empowering Facilitates the development of other math concepts

How is fact learning different from when I learned facts? 1. Facts are clustered in groups that can be retrieved by the same strategy. 2. Students can remember 6 to 8 strategies rather than 100 discrete facts. 3. Students achieve mastery of a group of facts employing one strategy before moving on to another group.

General Approach Introduce a strategy using association, patterning, contexts, concrete materials, pictures – whatever it takes so students understand the logic of the strategy Practice the facts that relate to this strategy, reducing wait time until a time of 3 seconds, or less, is achieved. Constantly discuss answers and strategies. Integrate these facts with others learned by other strategies. IT WILL TAKE TIME!

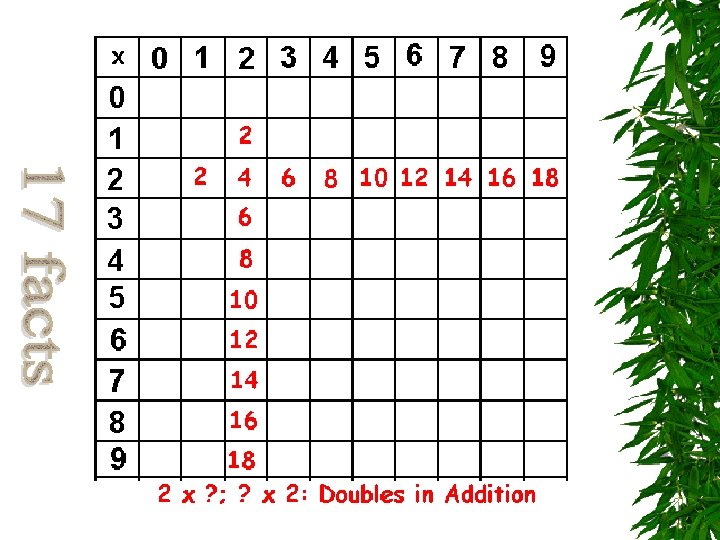
Facts with 2 s: 2 x ? and ? X 2 Strategy: Connect to Doubles in Addition Start with 2 x ? Relate ? X 2 to 2 x ?

Practice the Facts Webs Dice games Card games Flash cards

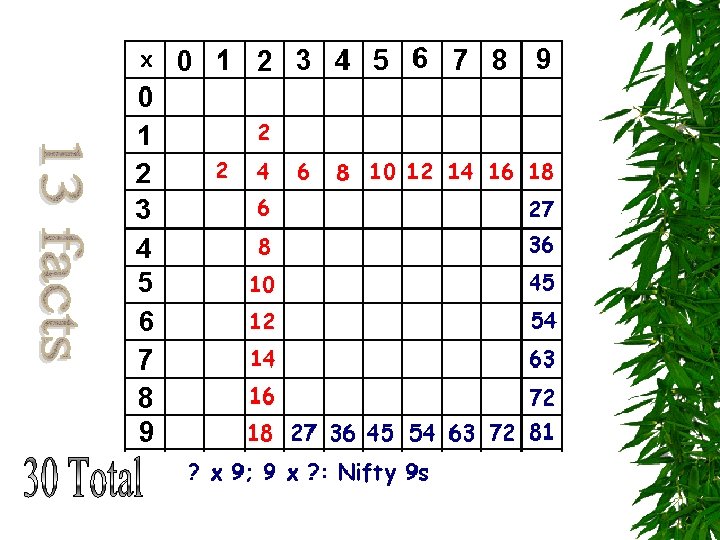
Facts with 9 s: ? X 9 and 9 x ? Nifty Nines Strategy: Two Patterns -Decade of answer is one less than the number of 9 s and the two digits of the answer sum to 9 9 x 9 = 81 8 x 9 = 72 7 x 9 = 63 6 x 9 = 54 5 x 9 = 45 4 x 9 = 36 3 x 9 = 27

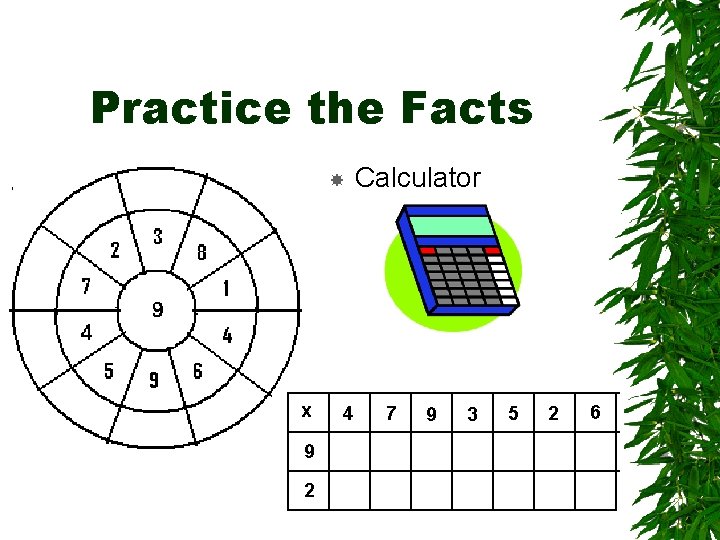
Practice the Facts Calculator

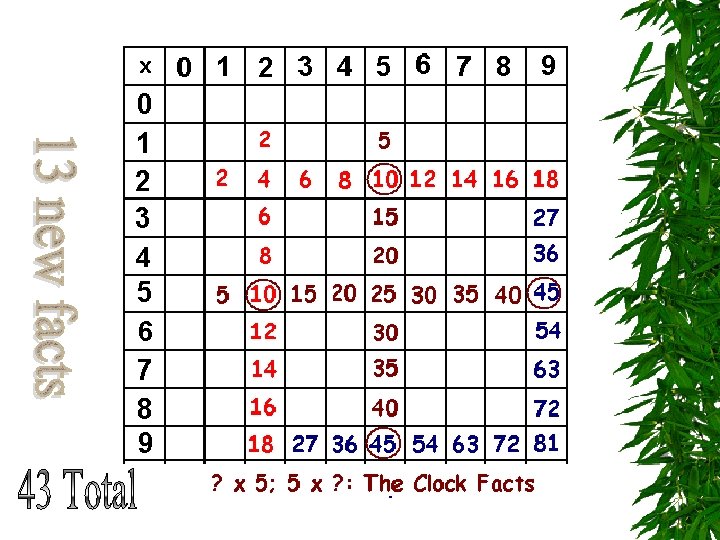
Facts with 5 s The Clock Strategy: The number of 5 s is like the minute hand on the clock – it points to the answer. For example, for 4 x 5, the minute hand on 4 means 20 minutes; therefore, 4 x 5 = 20.

Practice Strategy Selection Which facts can use The Clock Strategy? Which facts can use the Nifty Nines Strategy? Which facts can use the Doubles Strategy? 3 x 5 5 x 9 8 x 2 9 x 7 9 x 2 2 x 5 7 x 5 6 x 9

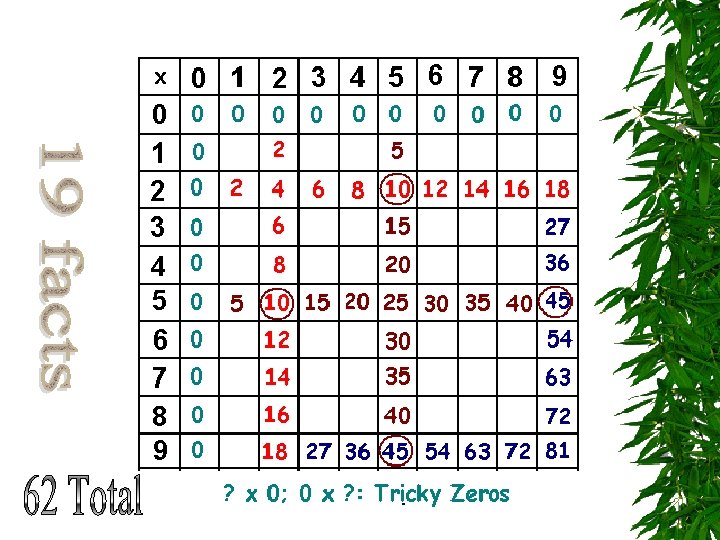
Facts with 0 s The Tricky Zeros: All facts with a zero factor have a zero product. (Often confused with addition facts with 0 s) If you have 6 plates with 0 cookies on each plate, how many cookies do you have?

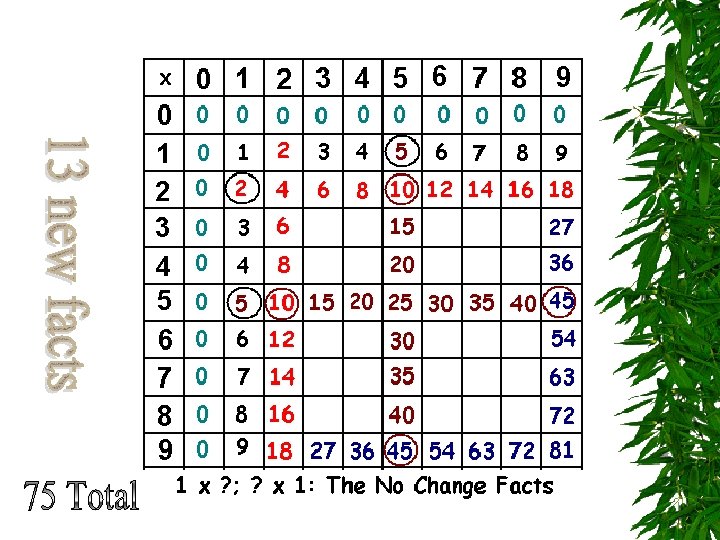
Facts with 1 s The No Change Facts: Facts with 1 as a factor have a product equal to the other factor. If you have 3 plates with 1 cookie on each plate OR 1 plate with 3 cookies on it, you have 3 cookies.

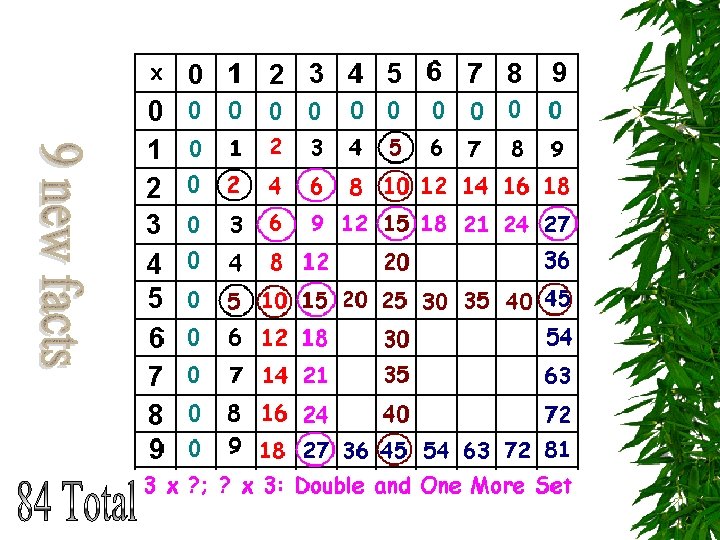
Facts with 3 s The Double and One More Set Strategy. For example, for 3 x 6, think: 2 x 6 is 12 plus one more 6 is 18.

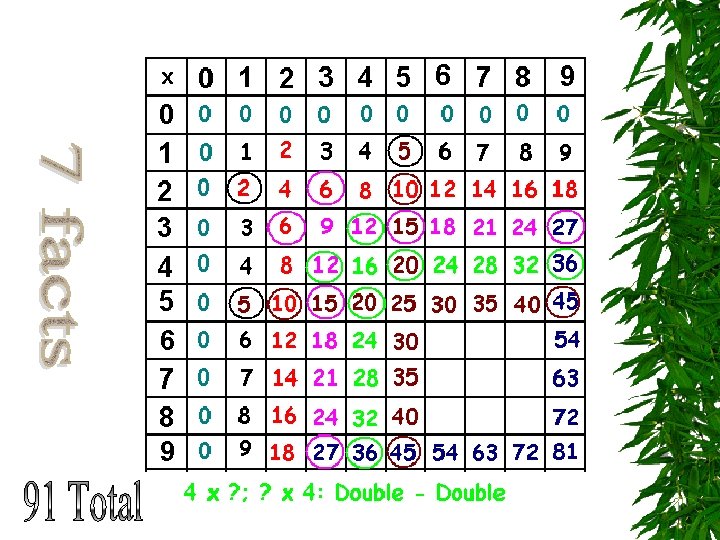
Facts with 4 s The Double Strategy. For example, for 4 x 6, think: double 6 is 12 and double 12 is 24.

The Last Nine Facts 6 x 6 6 x 7 and 7 x 6 6 x 8 and 8 x 6 7 x 7 7 x 8 and 8 x 7 8 x 8 • • Using helping facts: 6 x 6=5 x 6+6 7 x 6=5 x 6+2 x 6 6 x 8=5 x 8+8 7 x 8=5 x 8+2 x 8 8 x 8=4 x 8 x 2 Some know 8 x 8 is 64 because of a chess board What about 7 x 7?

Practice the Facts Flash cards Bingo Dice Games Card Games Fact Bee Calculators

Some Summary Statements ü Students have to developmentally ready if strategies are to be meaningful and integrated into students’ thought processes. ü Try to have the strategies come from students in your class who have invented them on their own. ü Make sure that strategies are explicitly discussed and understood well before they are drilled. ü Practice of the facts should be varied using visuals and oral language, using games, and using calculators, in whole class, partner, and individual situations.

Some Summary Statements ü ü ü The oral language used in practices can be varied. Initially you should use one phrase throughout a practice session, and build upon the various phrases until you use a variety of phrases in a single practice session. Facts for each strategy should be practiced on their own until they are efficiently recalled, and then integrated with facts using other strategies. Practice of facts should include discussion of the strategy(ies) used. After the introduction of three or more strategies, students should also practice strategy selection.

Some Summary Statements ü Time for a response might initially be 8 -10 seconds and with continued practice be narrowed until the 3 -second goal is achieved. (The timing is to promote the use of efficient mental strategies and to discourage finger counting and other external inefficient methods. ) ü When a strategy is introduced, students should examine new facts for this strategy as well as re -examine facts for which they already may have an alternative strategy.

Some Summary Statements ü In the end, the goal is to have students be able to give quick responses (3 seconds) to the addition facts. They may be using any of a number of techniques including the mental strategies you have discussed and practiced or they have invented, visualization strategies such as images of ten-frames or number lines, and simply memory from repetitive exposure. Any one student may be employing a variety of these techniques depending upon the particular facts they are responding to.

Find the Product 29 x 8

Underlying Understandings Facts Decomposition/Part- Whole Place Value Properties of Operations

From Multiplication Facts to Other Products Facts extended to 10 s, 1000 s 3 x 70, 3 x 7000 30 x 7, 3000 x 7

From Multiplication Facts to Other Products Multiplying/Dividing by 10, 1000: Shifting of Place Values 345 x 100 4. 56 x 1000 3. 02 100

From Multiplication Facts to Other Products Tens by Tens: It’s a question of how many hundreds 20 x 40 30 x 90 20 x 60

From Multiplication Facts to Other Products Front End: Start at highest place value and use distributive property 3 x 73 3 x 85 4 x 306 2 x 460

From Multiplication Facts to Other Products Compensation: Change to make it easier to multiply and fix the answer 6 x 39 99 x 56 58 x 4 5 x 698 2 x 2997

From Multiplication Facts to Other Products Re-association of Factors: Look for a compatible factor and use associative property 50 x 89 25 x 48 2. 5 x 64 500 x 62 250 x 88