Multiplication 1 Making Connections Haylock and Cockburn 2008

Multiplication 1

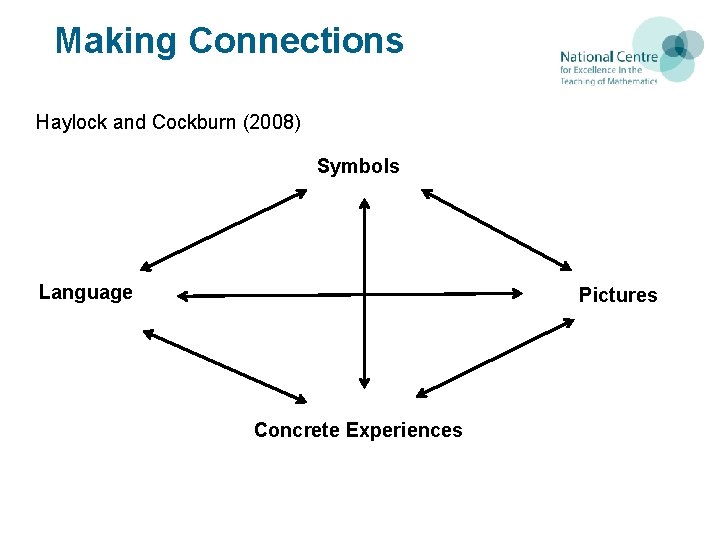
Making Connections Haylock and Cockburn (2008) Symbols Language Pictures Concrete Experiences 10

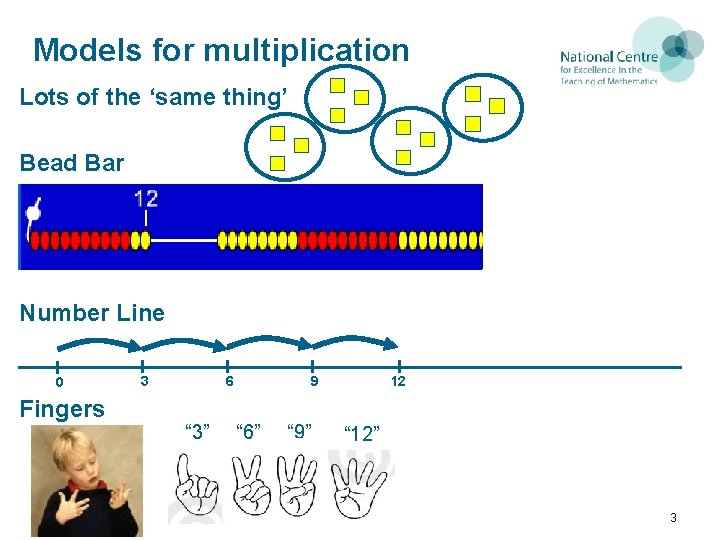
Models for multiplication Lots of the ‘same thing’ Bead Bar Number Line 0 Fingers 6 3 “ 3” 9 “ 6” “ 9” 12 “ 12” 3

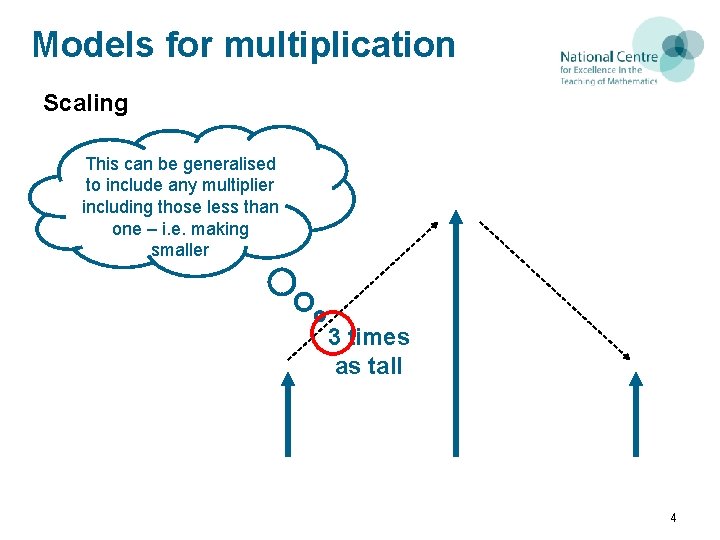
Models for multiplication Scaling This can be generalised to include any multiplier including those less than one – i. e. making smaller 3 times as tall 4

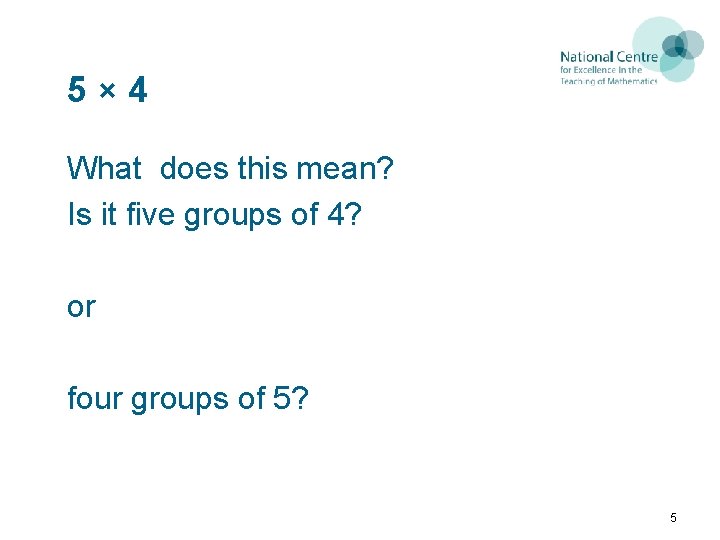
5× 4 What does this mean? Is it five groups of 4? or four groups of 5? 5

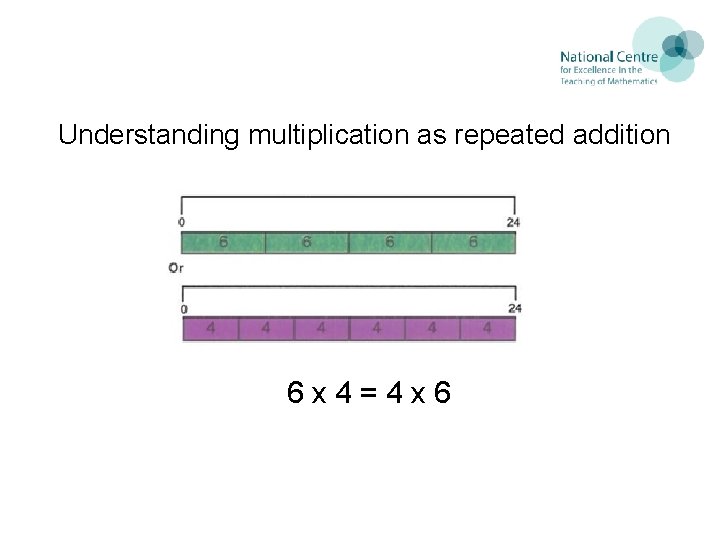
Understanding multiplication as repeated addition 6 x 4=4 x 6 11

Models for multiplication 3 4 4 3 7

An image for 7 8 = 56 8

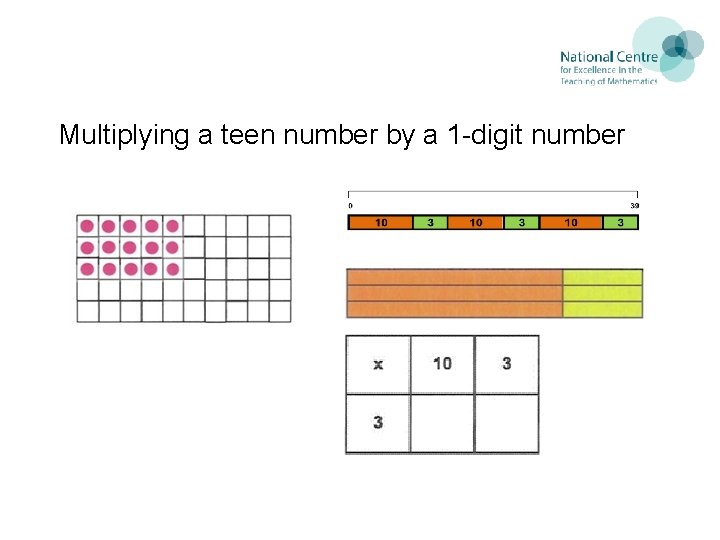
Multiplying a teen number by a 1 -digit number 18

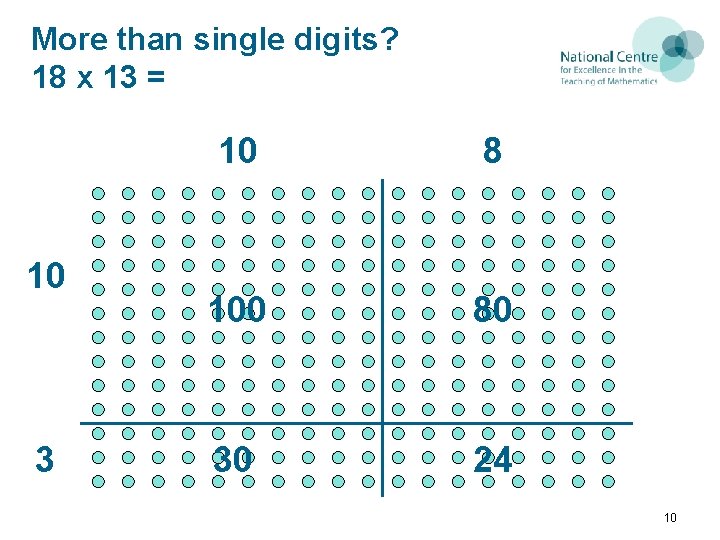
More than single digits? 18 x 13 = 10 10 13 3 18 8 100 80 30 24 10

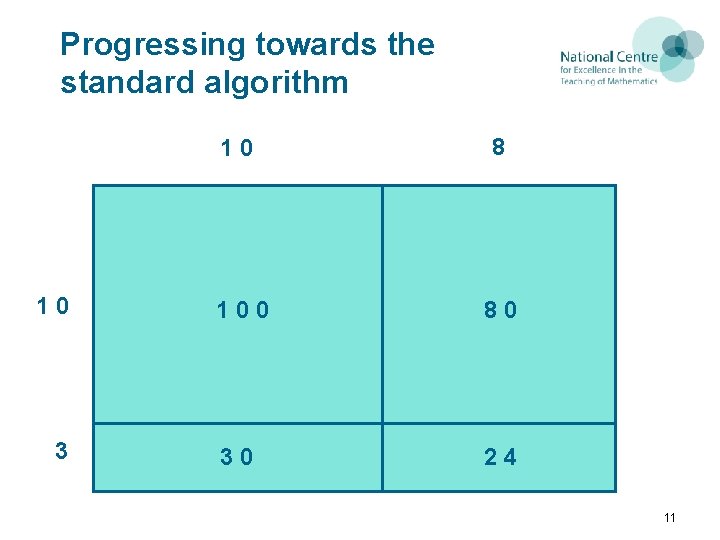
Progressing towards the standard algorithm 10 3 10 8 100 80 30 24 11

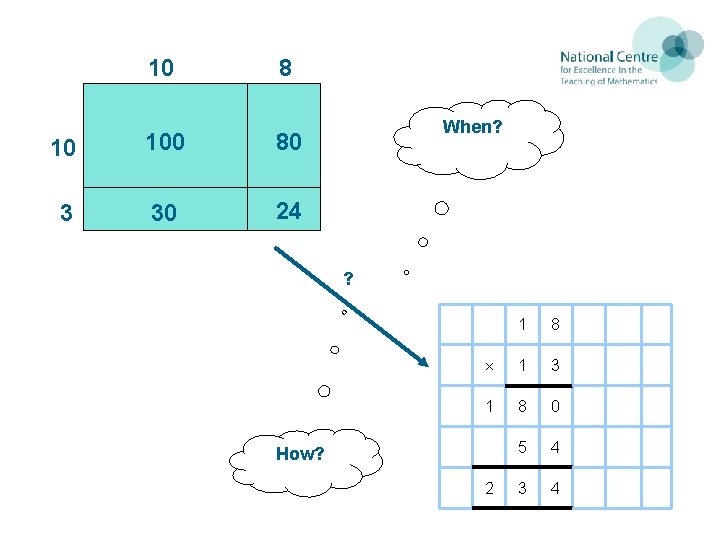
10 8 10 100 80 3 30 24 When? ? 1 8 1 3 1 8 0 5 4 3 4 How? 2

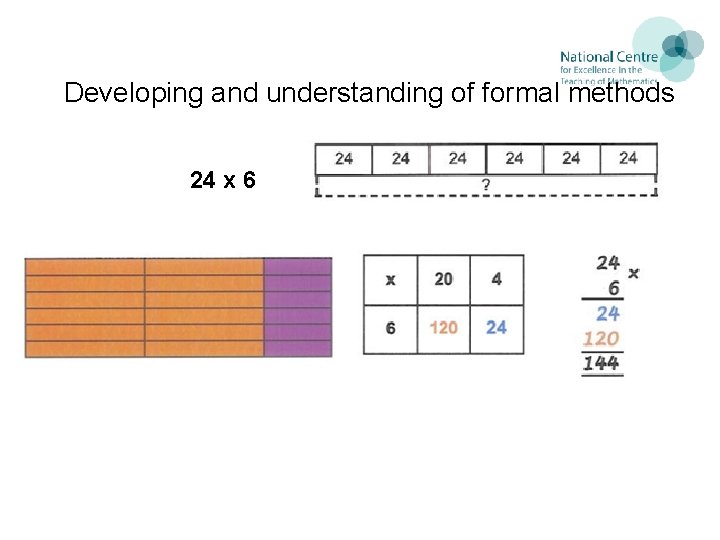
Developing and understanding of formal methods 24 x 6 20

Division

Sharing or Grouping What does each mean? Model each with some counters for 8 2 What’s the same? What’s different? 15

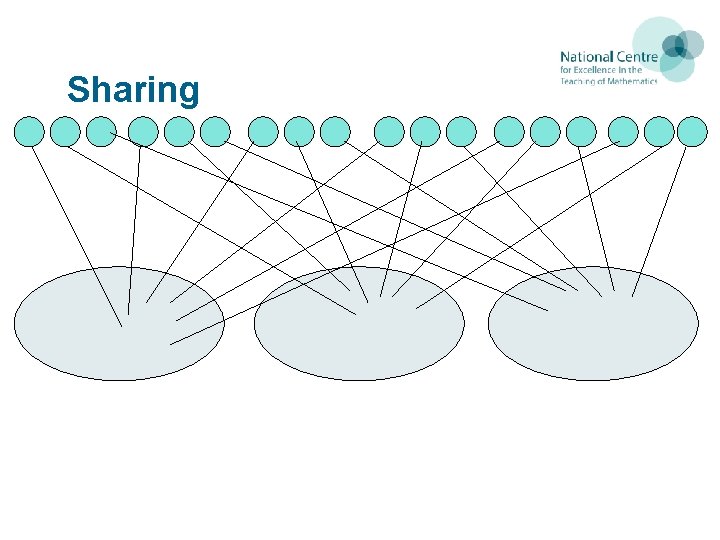
Sharing 10

Grouping 0 3 6 9 12 15 18 11

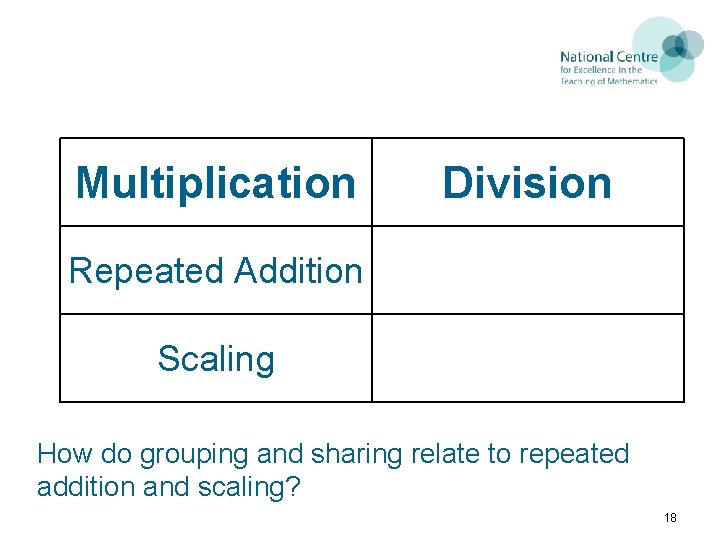
Multiplication Division Repeated Addition Scaling How do grouping and sharing relate to repeated addition and scaling? 18

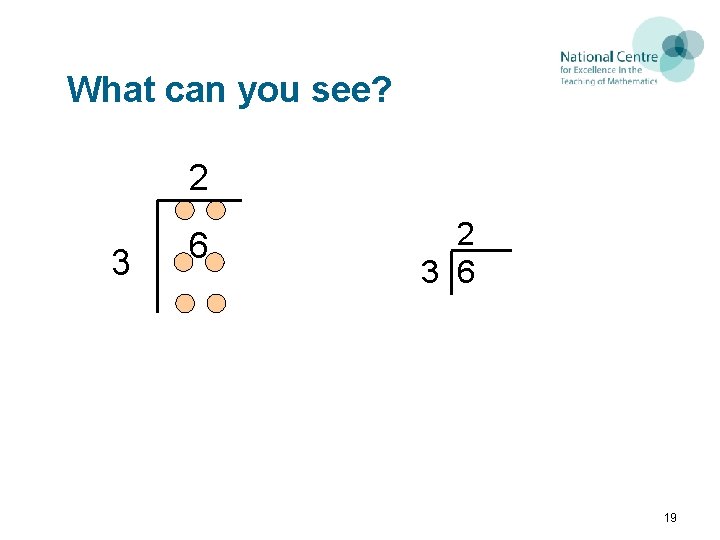
What can you see? 2 3 6 19

An image for 56 7 Either: • How many 7 s can I see? (grouping) Or: • If I put these into 7 groups how many in each group? (sharing)

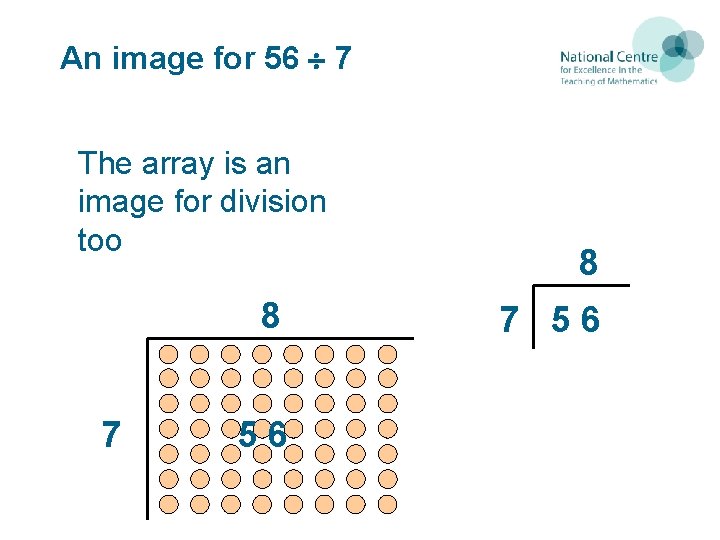
An image for 56 7 The array is an image for division too 8 7 56

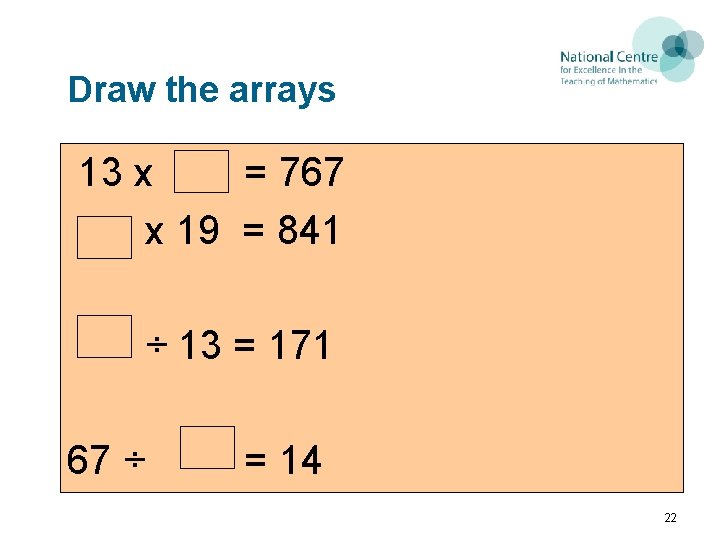
Draw the arrays 13 x = 767 x 19 = 841 ÷ 13 = 171 67 ÷ = 14 22

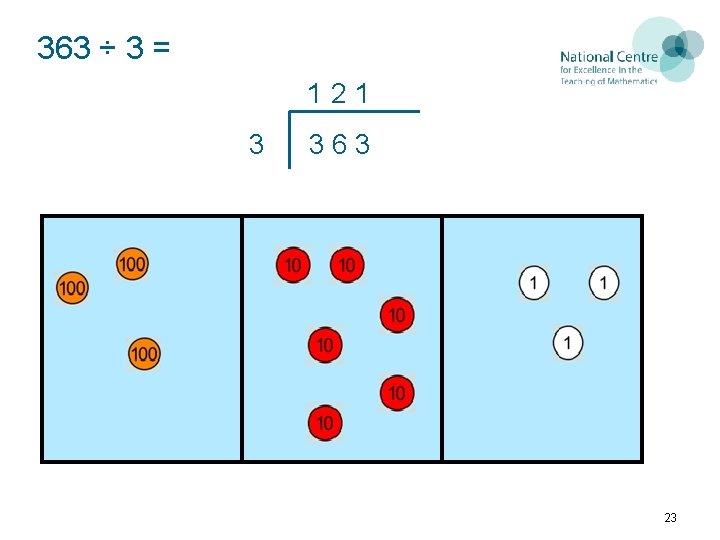
363 ÷ 3 = 121 3 363 23

Task Explore some division calculations using the different manipulatives. • How well do the manipulatives help you to solve the calculation problems? • How well do the manipulatives help to move pupils towards written methods? • Reflect on your own practice about how a written method for division can be taught. 24