Multiple Valued Logic Currently Studied for Logic Circuits

Multiple Valued Logic • Currently Studied for Logic Circuits with More Than 2 Logic States – Intel Flash Memory – Multiple Floating Gate Charge Levels – 2, 3 bits per Transistor http: //www. ee. pdx. edu/~mperkows/ISMVL/flash. html • Techniques for Manipulation Applied to Multioutput Functions – Characteristic Equation – Positional Cube Notation (PCN) Extensions

MVI Functions • Each Input can have Value in Set {0, 1, 2, . . . , pi-1} • MVI Functions • X is p-valued variable • literal over X corresponds to subset of values of S {0, 1, . . . , p-1} denoted by XS

MVL Literals • Each Variable can have Value in Set {0, 1, 2, . . . , pi-1} • X is a p-valued variable • MVL Literal is Denoted as X{j} Where j is the Logic Value • Empty Literal: X{ } • Full Literal has Values S={0, 1, 2, …, p-1} X{0, 1, …, p-1} Equivalent to Don’t Care

MVL Example • MVI Function with 2 Inputs X, Y – X is binary valued {0, 1} – Y is ternary valued {0, 1, 2} – n=2 p. X=2 p. Y=3 • Function is TRUE if: – – X=1 and Y= 0 or 1 Y=2 SOP form is: F = X{1}Y{0, 1} + X{0, 1}Y{2} • Literal X{0, 1} is Full, So it is Don’t Care – implicant is – minterm is X {1}Y{0} – prime implicants are X{1} and Y{2} X{1} Y{0, 1} F Y X 0 1 1 1 2 1 1

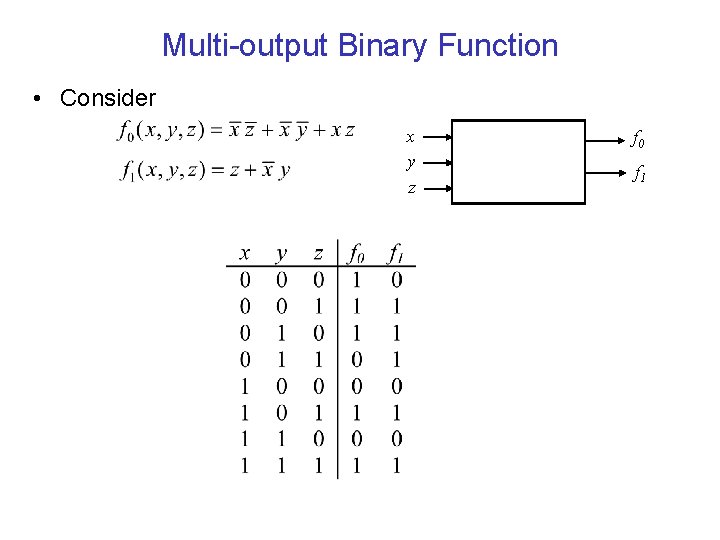
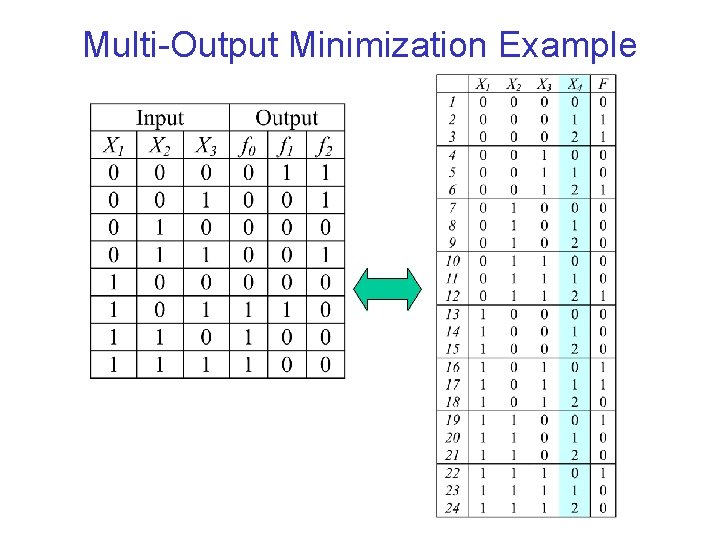
Multi-output Binary Function • Consider x y z f 0 f 1

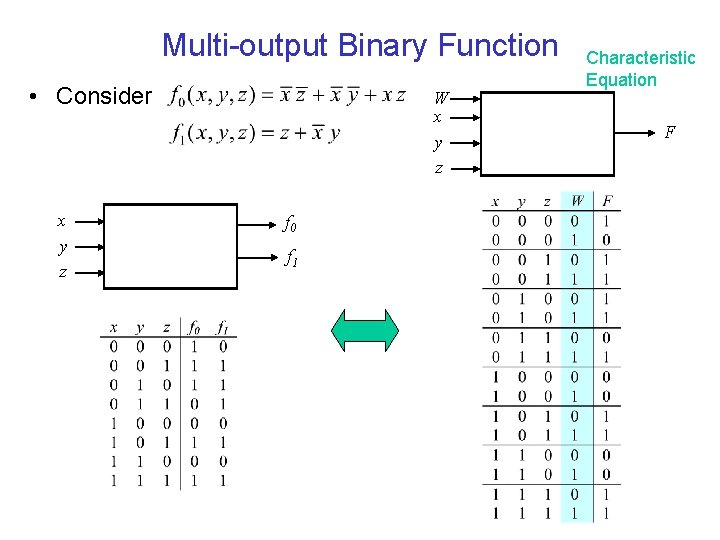
Multi-output Binary Function • Consider x y z W x y z f 0 f 1 Characteristic Equation F

Characteristic Equation Sum of Minterms

PCN for MVL Functions • Binary Variables, {0, 1}, Represented by 2 -bit Fields 00 0 10 1 01 * 11 • MV Variables, {0, 1, …, p-1}, Represented by p-bit Fields • BV Don’t Care is 11 • MV Don’t Care is 111… 1 • MV Literal or Cube is Denoted by C( )

PCN for MVL Example • Positional Cube Corresponding to X{1} is C(X{1}) • Since Y{0, 1, 2} is Don’t Care

PCN for MVI-BO Example z a b f 1 f 2 f 3 a b 10 10 100 a b 10 01 001 a b 01 10 001 ab 01 01 110 • View This as a SOP of MVI Function: • F is the Characteristic Equation

List Oriented Manipulation • Size of Literal = Cardinality of Logic Value Set x{0, 2} size = 2 • Size of Implicant (Cube, Product Term) = Integer Product of Sizes of Literals in Cube • Size of Binary Minterm = 1 Implicant of Unit Size EXAMPLE f (x 1, x 2, x 3, x 4, x 5, x 6)

Logic Operations • Consider Implicants as Sets – Apply ( , , , etc) • Apply Bitwise Product, Sum, Complement to PCN Representation • Bitwise Operations on Positional Cubes May Have Different Meaning than Corresponding Set Operations EXAMPLE Complement of Implicant Complement of Positional Cube

MVL Logical Operations • AND Operation – MIN - Set Intersection • OR Operation – MAX - Set Union • NOT Operation – Set Complement EXAMPLE

MVL Number of Functions of 1 Variable

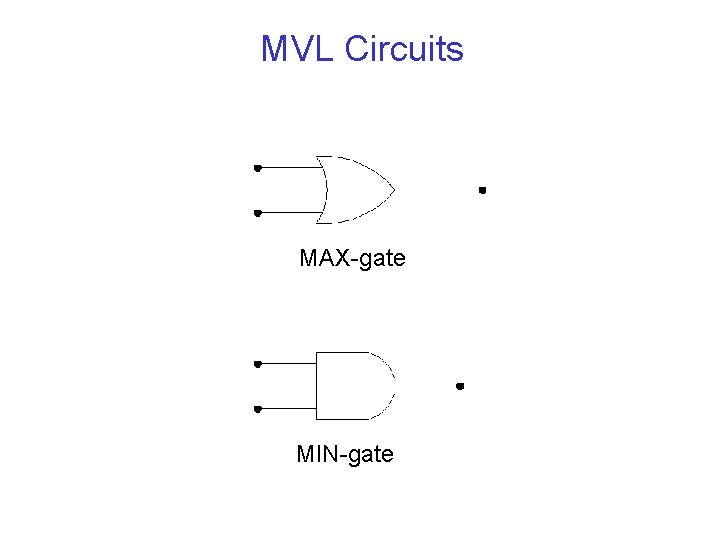
MVL Circuits MAX-gate MIN-gate

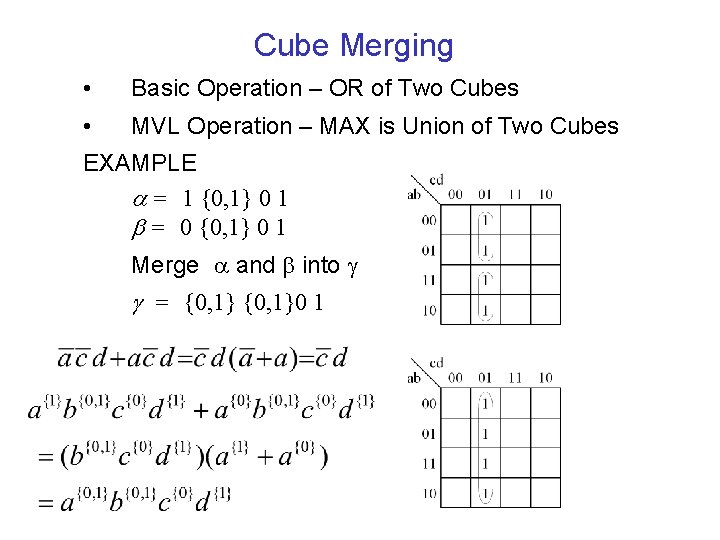
Cube Merging • Basic Operation – OR of Two Cubes • MVL Operation – MAX is Union of Two Cubes EXAMPLE = 1 {0, 1} 0 1 = 0 {0, 1} 0 1 Merge and into = {0, 1}0 1

Multi-Output Minimization Example

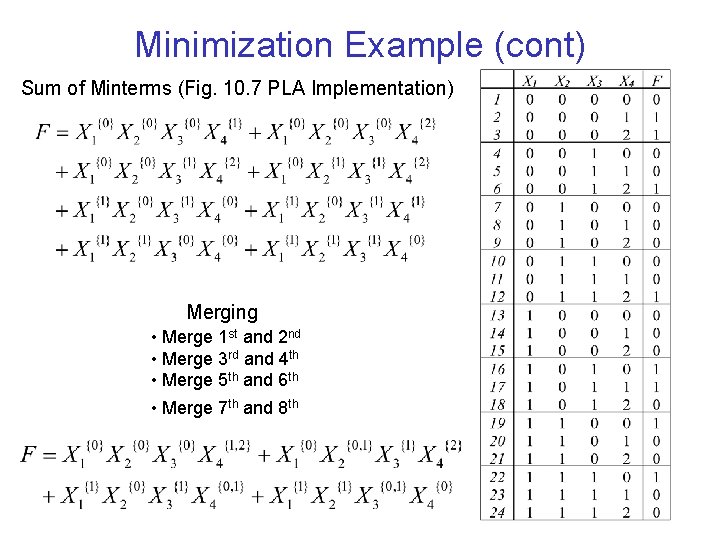
Minimization Example (cont) Sum of Minterms (Fig. 10. 7 PLA Implementation) Merging • Merge 1 st and 2 nd • Merge 3 rd and 4 th • Merge 5 th and 6 th • Merge 7 th and 8 th

Minimization Example (cont) Multi-Output Function Using of Multi-Output Prime Implicants (Fig. 10. 8 PLA Implementation)