Multiple Sequence Alignment I Lecture for CS 498

Multiple Sequence Alignment (I) (Lecture for CS 498 -CXZ Algorithms in Bioinformatics) Oct. 4, 2005 Cheng. Xiang Zhai Department of Computer Science University of Illinois, Urbana-Champaign

Outline • Motivation • Scoring of multiple sequence alignments • Algorithms – Dynamic programming – Progressive alignment (next class)

Why Multiple Alignments? • Characterize protein families: Identify shared regions of homology in a multiple sequence alignment • Determination of the consensus sequence of several aligned sequences. • Help predict the secondary and tertiary structures of new sequences • Help predict the function of new sequences • Preliminary step in molecular evolution analysis using phylogenetic trees.

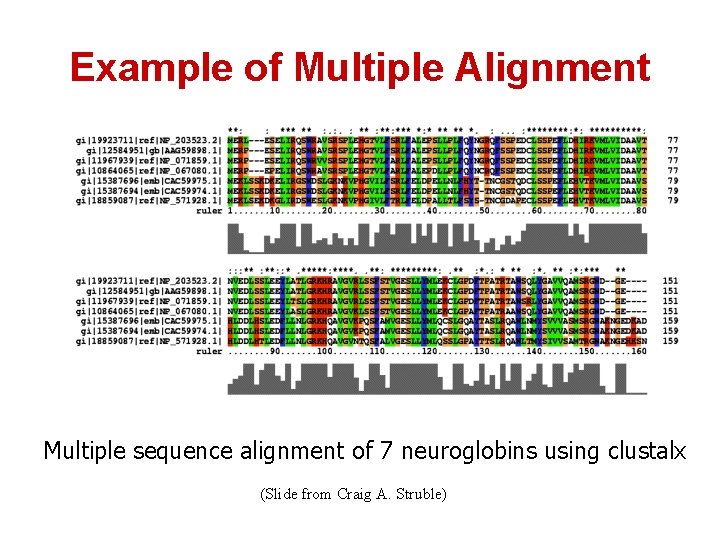
Example of Multiple Alignment Multiple sequence alignment of 7 neuroglobins using clustalx (Slide from Craig A. Struble)

4 Basic Questions in Multiple Alignment Q 1: How should we define s? X 1=x 11, …, x 1 m 1 Q 2: How should we define A? Model: scoring function s: A X 1=x 11, …, x 1 m 1 Possible alignments of all Xi’s: A ={a 1, …, ak} X 2=x 21, …, x 2 m 2 … Find the best alignment(s) XN=x. N 1, …, x. Nm. N Q 3: How can we find a* quickly? X 2=x 21, …, x 2 m 2 S(a*)= 21 … XN=x. N 1, …, x. Nm. N Q 4: Is the alignment biologically Meaningful?

Defining Multi-Sequence Alignment • We may generalize our definition of pairwise sequence alignment • Alignment of 2 sequences is represented as a 2 -row matrix • In a similar way, we represent alignment of 3 sequences as a 3 -row matrix A T _ G C G _ A _ C G T _ A A T C A C _ A • A column must have at least one nucleotide • Question: How many possible global alignments are there for 3 sequences each of length 2?

How do we score a multiple alignment?

Scoring a Multiple Alignment • Ideally, it should be based on evolutionary models • In practice, – We often assume columns are independent G is the gap score – Use “Sum of Pairs” (SP scores)

Minimum Entropy Scoring Intuition: A perfectly aligned column has one single symbol (least uncertainty) A poorly aligned column has many distinct symbols (high uncertainty) Count of symbol a in column i This is related to the HMM formulation of the alignment problem, which we will cover later …

Entropy: Example Best case Worst case

Entropy of an Alignment: Example column entropy: -( p. Alogp. A + p. Clogp. C + p. Glogp. G + p. Tlogp. T) A A A • Column 1 = -[1*log(1) + 0*log 0 +0*log 0] =0 A C C • Column 2 = -[(1/4)*log(1/4) + (3/4)*log(3/4) + 0*log 0] = -[ (1/4)*(-2) + (3/4)*(-. 415) ] = +0. 811 A C G A C T • Column 3 = -[(1/4)*log(1/4)+(1/4)*log(1/4)] = 4* -[(1/4)*(-2)] = +2 • Alignment Entropy = 0 + 0. 811 + 2 = +2. 811

How can we find a multiple alignment quickly? Can we generalize the dynamic programming algorithm used for pairwise alignment?

Alignments = Paths in… • Align 3 sequences: ATGC, AATC, ATGC A -- T G C A A T -- C -- A T G C

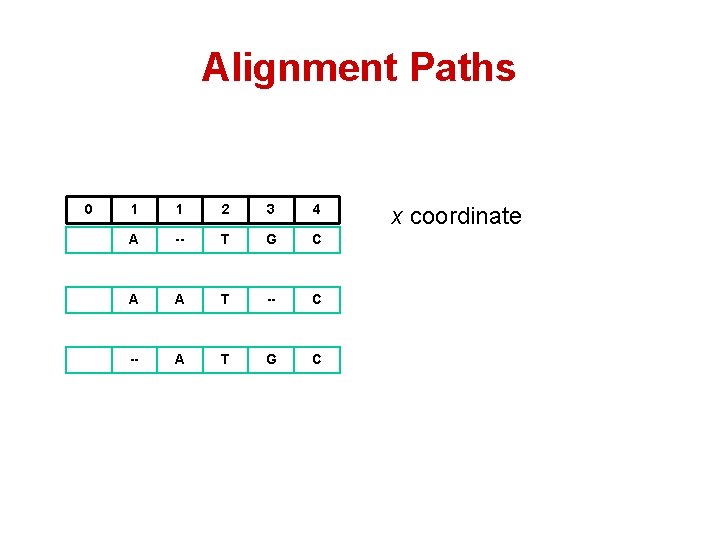
Alignment Paths 0 1 1 2 3 4 A -- T G C A A T -- C -- A T G C x coordinate

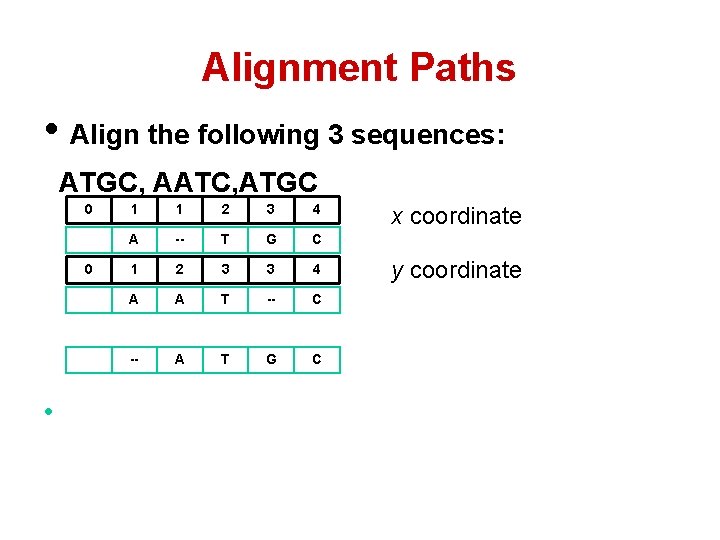
Alignment Paths • Align the following 3 sequences: ATGC, AATC, ATGC 0 0 • 1 1 2 3 4 A -- T G C 1 2 3 3 4 A A T -- C -- A T G C x coordinate y coordinate

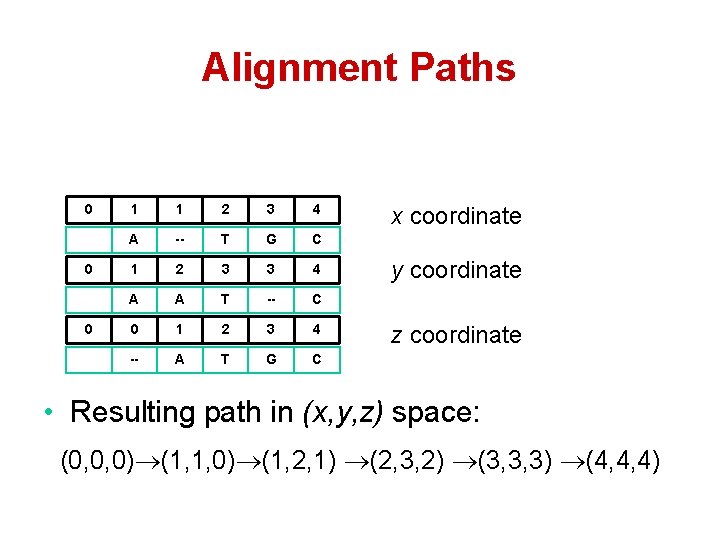
Alignment Paths 0 0 0 1 1 2 3 4 A -- T G C 1 2 3 3 4 A A T -- C 0 1 2 3 4 -- A T G C x coordinate y coordinate z coordinate • Resulting path in (x, y, z) space: (0, 0, 0) (1, 1, 0) (1, 2, 1) (2, 3, 2) (3, 3, 3) (4, 4, 4)

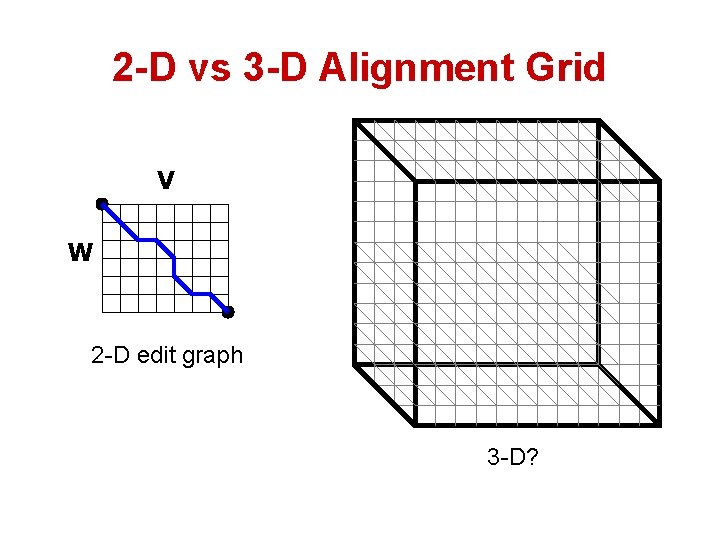
2 -D vs 3 -D Alignment Grid V W 2 -D edit graph 3 -D?

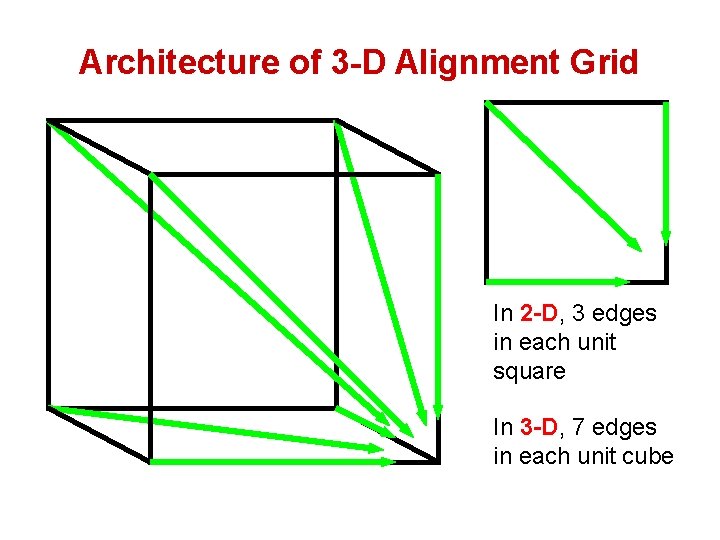
Architecture of 3 -D Alignment Grid In 2 -D, 3 edges in each unit square In 3 -D, 7 edges in each unit cube

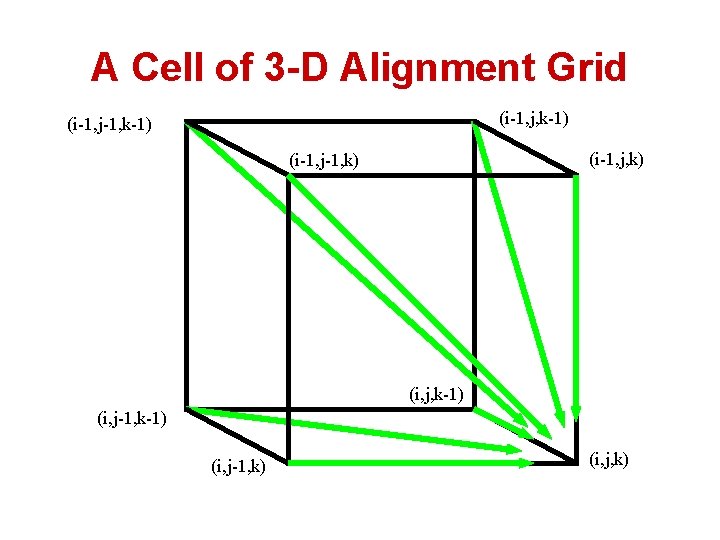
A Cell of 3 -D Alignment Grid (i-1, j, k-1) (i-1, j-1, k-1) (i-1, j, k) (i-1, j-1, k) (i, j, k-1) (i, j-1, k) (i, j, k)

Multiple Alignment: Dynamic Programming • si, j, k = max si-1, j-1, k-1 + (vi, wj, uk) si-1, j-1, k + (vi, wj, _ ) si-1, j, k-1 + (vi, _, uk) si, j-1, k-1 + (_, wj, uk) si-1, j, k + (vi, _ , _) si, j-1, k + (_, wj, _) si, j, k-1 + (_, _, uk) cube diagonal: no indels face diagonal: one indel edge diagonal: two indels • (x, y, z) is an entry in the 3 -D scoring matrix and can be computed using sum of pairs or entropy

Multiple Alignment: Running Time • For 3 sequences of length n, the run time is 7 n 3; O(n 3) • For k sequences, building a k-dimensional edit graph has run time (2 k-1)(nk); O(2 knk) • Conclusion: dynamic programming approach for alignment between two sequences is easily extended to k sequences but it is impractical due to exponential running time

In the next class, we will cover more efficient algorithms -progressive alignment ….

What You Should Know • How to score a multi-sequence alignment • How the dynamic programming algorithm works • Computational complexity of dynamic programming algorithms