Multiple Sequence alignment Chitta Baral Arizona State University

Motivation and Introduction • Need for multiple sequence alignment – We have the sequences of several proteins which have similar function in a number of different species – We may want to know which part of these sequences are similar and which parts are different. • What is multiple alignment? – Let s 1, …, sk be a set of sequences over the same alphabet. – Spaces are inserted in s 1, …, sk to make them all of same size. – When the extended sequences are aligned, no column can be made exclusively of spaces. – An example • • MQPILLL ML R-LLMK - ILLL M P PV L I L – First important issue: defining the quality of an alignment.

The `sum-of-pairs’ (SP) measure • Requirement of a good quality of alignment measure – Additive function – Function must be independent of order of arguments – Should reward presence of many equal or strongly related symbols (in the same column) and penalize unrelated symbols and spaces. • SP function: sum of pairwise scores of all pairs of symbols in the column – SP-score(I, -, I, V) = s(I, -) + s(I, I) + s(I, V) + s(-, I) + s(-, V) + s(I, V). – s(-, -) = 0. • Theorem: Let alpha be a multiple alignment of the set of sequences s 1, …, sk; and alpha(I, j) denote the pairwise alignment of si and sj as induced by alpha. Then SP-score(alpha) = Sum over i, j [score(alpha(i, j)] – The above is only true if we have s(-, -) = 0. – This is because in pairwise alignment the presence of two aligned spaces (–) in the two sequences are ignored.

Optimal alignment using dynamic programming • • Consider k sequences, each of length n Use a k-dimensional array A[] of length n+1 in each dimension Initialize A[0, …, 0] = 0. A[i 1, …, ik] max b {A[i-b] + SP-score(Column(s, i, b))} – – • Where b ranges over all non-zero binary vectors of k elements, and Column(s, i, b) = (cj) 1<= j <= k With cj = sj[ij] if bj=1 and cj=- if bj = 0. Boldface indicates k-tuples. A[i 1, i 2, i 3] max of – – – – A[i 1, i 2, i 3 -1] + SP-score(-, -, s 3[i 3]) A[i 1, i 2 -1, i 3] + SP-score(-, s 2[i 2], -) A[i 1, i 2 -1, i 3 -1] + SP-score(-, s 2[i 2], s 3[i 3]) A[i 1 -1, i 2, i 3] + SP-score(s 1[i 1], -, -) A[i 1 -1, i 2, i 3 -1] + SP-score(s 1[i 1], -, s 3[i 3]) A[i 1 -1, i 2 -1, i 3] + SP-score(s 1[i 1], s 2[i 2], -) A[i 1 -1, i 2 -1, i 3 -1] + SP-score(s 1[i 1], s 2[i 2], s 3[i 3])

Complexity analysis of the dynamic programming algorithm • Running time: – (n+1)k number of entries in the table – For each entry we need to find the maximum of 2 k -1 elements – Finding the SP-score corresponding to each element means adding O(k 2) numbers – Total = O(k 22 knk) i. e. , exponential w. r. t. k.

A heuristic based approach • Outline of the approach – We have k sequences of length n each and we want to compute the optimal alignments according to the SP measure – We use dynamic programming, but try to avoid filling all entries of the k-dimensional array, and fill only the `relevant’ relevant ones. • Which cells are relevant and why – Idea: look at pairwise projections of cells. – Note: Optimal alignments may not lead to pairwise projections that are optimal. • • • A T A – - T A T is optimal, but A _ and _ T are not optimal.

Heuristics based approach … cont • Recall F(i, j) meant the score of the best alignment between the initial segment x 1…i and y 1…j. Lets denote it by sim(x[1. . i], y[1. . j]), and refer to it as axy[i, j]. • I. e. , axy[i, j] = sim(x[1. . i], y[1. . j]). • Let bxy[i, j] = sim(x[i+1. . n], y[j+1. . m]). – Computed like axy but backwards. • And cxy[i, j] = axy[i, j] + bxy[i, j]. – Means the highest score of an alignment that cuts at (i, j) • Using the c matrix it is very easy to find the alignment. – Find a path from [n, m] to [0, 0] that has the value cxy[n, m] all through. • Suppose we know a lower bound Lxy for cxy. I. e. we know for sure that sim(x, y) >= Lxy. – In that case, cxy[i, j] < Lxy means the cut through (i, j) does not lead to the best alignment.

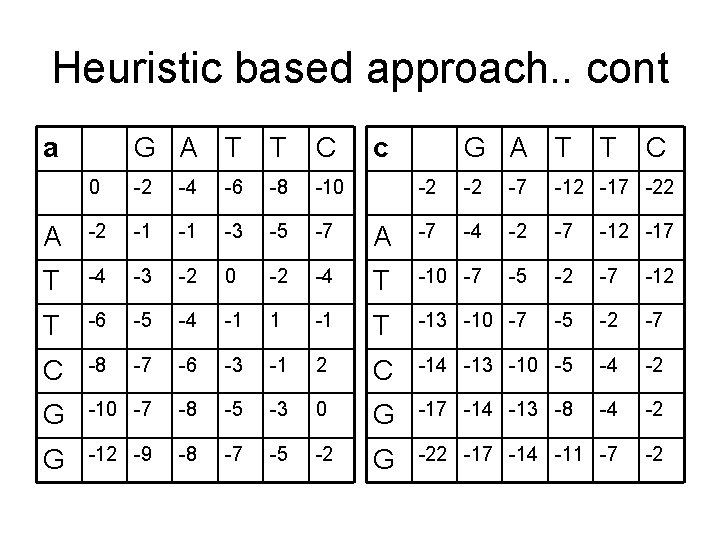
Heuristic based approach. . cont a G A T T C 0 -2 -4 -6 -8 -10 A -2 -1 -1 -3 -5 -7 T -4 -3 -2 0 -2 T -6 -5 -4 -1 C -8 -7 -6 G -10 -7 G -12 -9 c G A T T C -2 -2 -7 -12 -17 -22 A -7 -4 -2 -7 -12 -17 -4 T -10 -7 -5 -2 -7 -12 1 -1 T -13 -10 -7 -5 -2 -7 -3 -1 2 C -14 -13 -10 -5 -4 -2 -8 -5 -3 0 G -17 -14 -13 -8 -4 -2 -8 -7 -5 -2 G -22 -17 -14 -11 -7 -2

H. B. A (cont) – A theorem • Theorem: Let a be an optimal alignment involving s 1, …, sk. If SP-score(a) >= L then score(aij) > = Lij , where Lij = L – Sx<y & (x, y) == (i, j) (sim(sx, sy)). Proof: • Implication of this theorem: • • – SP-score(a) >= L iff Sx<y score(axy) > = L – iff Sx<y & (x, y) == (i, j) score(axy) > = L - score(aij) – Implies Sx<y & (x, y) == (i, j) (sim(sx, sy)) > = L - score(aij) ##because sim(sx, sy) is the best score and hence is greater than or equal to score(axy). – iff score(aij) > = L – Sx<y & (x, y) == (i, j) (sim(sx, sy)). – Suppose we have a lower bound L of SP-score, over all possible alignments. – Then a cell with index (i 1, …, ik) is relevant if the score of the best alignment (say a) that cuts through (i 1, …, ik) > = L – By theorem, this implies for all x, y, 1 <= x <y <= k we have score(axy) > = Lxy – Which means cxy (ix, iy) > = Lxy – This is because the best alignment will cut through ix iy. Idea of the algorithm: – Pick a lower bound L; Compute cxy and Lxy for each pair x, y 1 < = x < y < = k. – Start with (0, …, 0) and expand its influence to dependent relevant cells and continue until the final corner cell is reached.

The heuristic based algorithm • • • Input: s = (s 1, …, sk) and lower bound L Output: The value of an optimal alignment For all x, y, 1 <=x<y<=k Compute cxy For all x, y, 1 <=x<y<=k Lxy L - S(x, y) == (p, q) (sim(sp, sq)). pool {0} While pool not empty do – i the lexicographically smallest cell in the pool – pool {i} – If cxy[ix, iy]>= Lxy, forall x, y, 1 <= x<y<=k then • For all j dependent on i do – If j not in pool then pool U {j}; a[j] a[i] + SP-score(Column(s, i, j-i)) – else a[j] max( a[j], a[i] + SP-score(Column(s, i, j-i)) • Return a[n 1, …, nk]

Star alignment • Let s 1, …, sk be k sequences that we want to align • Pick one of the sequences sc as the center – For each index i == c find optimal alignment between si and sc – Aggregate these alignment using ``once a gap always a gap principle’’ • Start with one pair of alignment and keep adding alignment with respect to another string using sc as a guide by adding gaps when necessary • One way to select sc is to try all possibilities and pick the one that results in the best score. • Another way is to compute all optimal pairwise alignments and select as the center the string that maximizes Si == c sim(si, sc).

Tree alignment • Motivation: Sometimes we have an evolutionary tree for the sequences involved. – In that case we can compute the overall similarity based on pairwise alignment along tree edges. • Input: k sequences and a tree with leaves as these sequences. • Goal: Find a sequence asignment to the internal nodes of the tree so that the sum of the similarity between the sequences along each edges is maximized. • Tree alignment is NP-hard, but approximation algorithms exist. • Note: Star alignment can be viewed as a special case of tree alignment.