Multiple Sequence Alignment By Yuan Li Multiple Sequence

Multiple Sequence Alignment By Yuan Li

Multiple Sequence Alignment Lots of foundational problems in molecular biology are NP-hard Multiple Sequence Alignment Phylogeny Construction DNA sequencing (Shorest Common Superstring) RNA Structure Crossing Alignment K-mean Clustering

Multiple Sequence Alignment A sequence alignment of three or more biological sequences, generally protein, DNA, or RNA The input set of sequences share a lineage and a common ancestor Sequence homology can be inferred and phylogenetic analysis can be conducted to MSA Be used to access sequence conservation of proteins domain, DNA primary/secondary/tertiary structures

Pairwise Alignment Mutations: substitution, insertion, deletion Input: Given two sequences, s 1 and s 2 Output: The least number of mutations needed to convert s 1 to s 2, which is also the distance between s 1 and s 2 Example: S 1 = AAGG–TGC S 2 = A– GTATCC d(s 1, s 2) = 4

Multiple Sequence Alignment Input: a set of n sequences, {s 1, s 2, . . . , sn} Output: a n*L matrix, so that a certain criteria is optimal Input: GTAAC, GTAC Output: GTAAC - TAAC GTA- C Criteria: sum of pairs score, star align, tree align

Star Align - Optimization Input: Given a set of strings S={s 1, s 2, . . . , sn} Output: a optimal string c, such that the sum of distance between c and si (where 1<=i<=n), is minimum.

Star Align - Decision Input: Given a set of strings S={s 1, s 2, . . . , sn}, and a interger k Question: Is there a string c, such that the sum of distance between c and si (where 1<=i<=n), is less or equal to k?

NPC Problem 1) It is a decision problem 2) It is in the set NP Given a string c, the sum of distance between c and every string in S can be calculated in polynomial time and thus verify the correctness 3) Reduce to Vertex Cover Given ins(VC), an arbitrary instance of VC, construct an instance of star align, ins(SA) Proof that ins(VC) is true iff ins(SA) is true

Reduction Vertex Cover A graph (V, E) Star Alignment A set of strings, S |V|=n, |E|=m Minimum cover, v' A optimal string, c=DDCDD

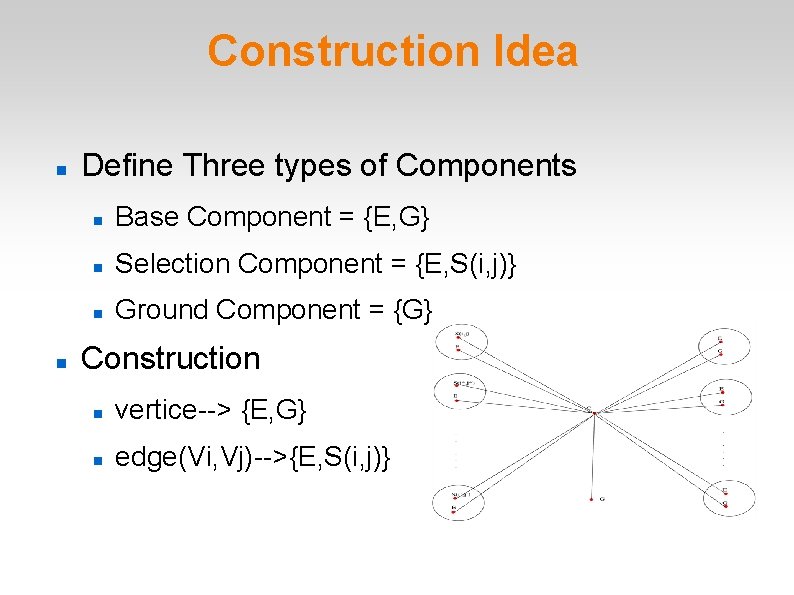
Construction Idea Define Three types of Components Base Component = {E, G} Selection Component = {E, S(i, j)} Ground Component = {G} Construction vertice--> {E, G} edge(Vi, Vj)-->{E, S(i, j)}

Definition Paddings, P 0 s 1 s 0 s, s>=(n+1) 0. . 0 1. . 1 0. . 0 Block 1, B 1 (vertex position = 1) Block 0, B 0 (vertex position = 0) P 1 P, i. e. 0. . 0 1. . 1 0. . 0 P 0 P, i. e. 0. . 0 1. . 1 0. . 0 0 0. . 0 1. . 1 0. . 0 String for vertex i, Vi (B 0)i-1 B 1(B 0)n-i

Definition Delimiter String, D 1111111. . . 111111, of length |Vi| Cover String, C (B 1|B 0)n Base String, c = DDCDD Enforcing String, E = DD (B 1)n DD Ground String, G = DD (B 0)n DD Selection String, S(i, j) = Vi. DVj

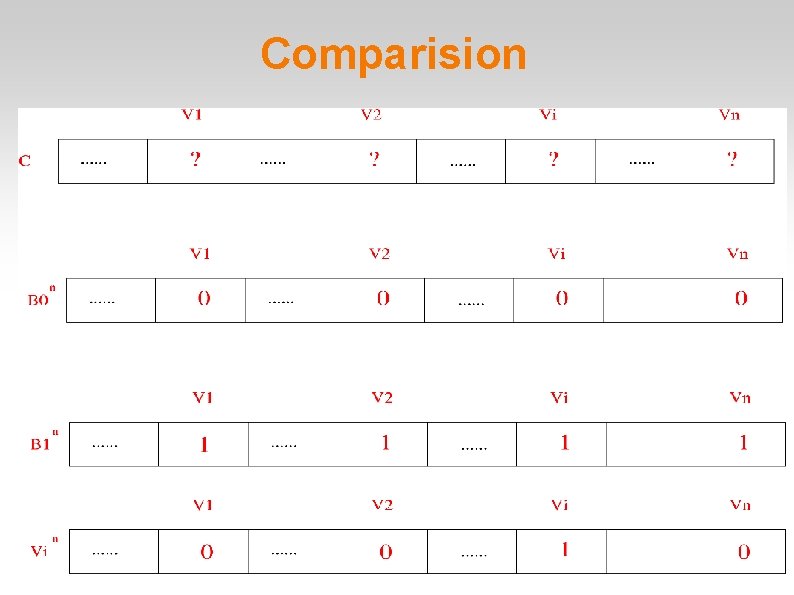
Comparision

Base Component {E, G} # = n, for each vertex, construct a base component {E, G} E = DD (B 1)n DD G = DD (B 0)n DD Lemma The only optimal alignment of E and G is the direct match If d(E, x)+d(G, x)<d(E, G)+1, x is base string, DDCDD.

Selection Component {E, S(i, j)} # = m, for each edge(vi, vj), construct a selection component E, S(i, j) E = DD (B 1)n DD, votes 1 in all vertex positions. S(i, j) = Vi D Vj, votes 0 in all except vertex position i or j, so that either vertex i or vertex j is part of the vertex cover DD | C|DD Vi D | Vj | | Vi | D Vj

Ground Component {G} # = 1, only construct one ground component G = DD(B 0)n DD c = DDCDD d(G, c) means align . . 0. . . . ? . . . G will penalze each 1 in vertex positions, so that the sum of d(c, si) is minimum <--> the size of vertex cover v' is minimum.

Component Base component {E, G} → c = DDCDD Selection component {E, S(i, j)} →c <--> Vertex Cover Ground component {G} →minimum cover

Conclusion Vertex Cover is a NP-Complete Problem Vertex Cover can be transformed to Star Alignment in polynomial time So that Star Alignment is also a NP-Complete Problem

Reference Isaac Elias, Settling the intractability of multiple alignment, in Proc. of the 14 th Ann. Int. Symp. on Algorithms and Computation (ISAAC), 2003, p 352 -363