Multiple regression Regression Problem to draw a straight

Multiple regression
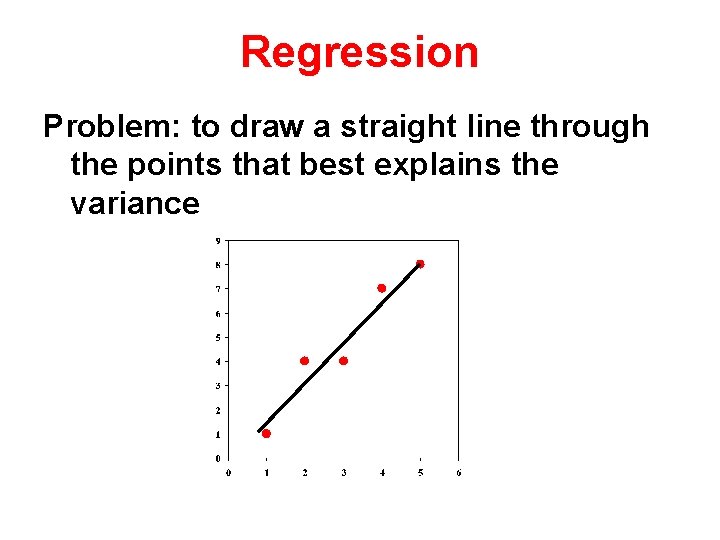
Regression Problem: to draw a straight line through the points that best explains the variance
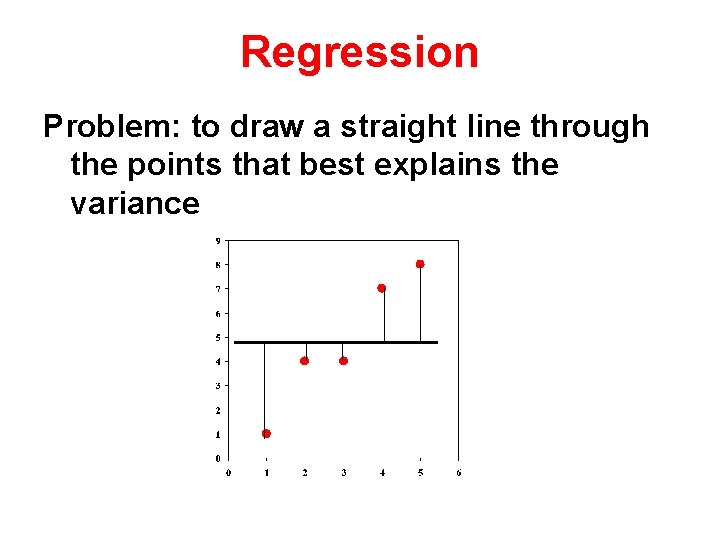
Regression Problem: to draw a straight line through the points that best explains the variance
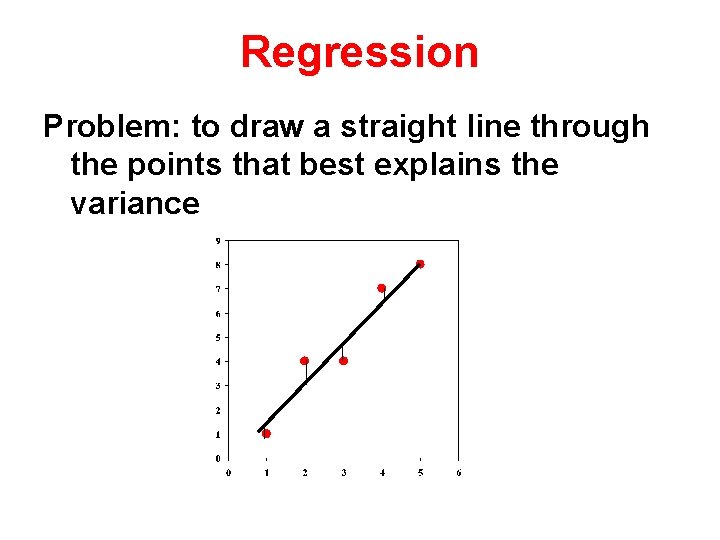
Regression Problem: to draw a straight line through the points that best explains the variance
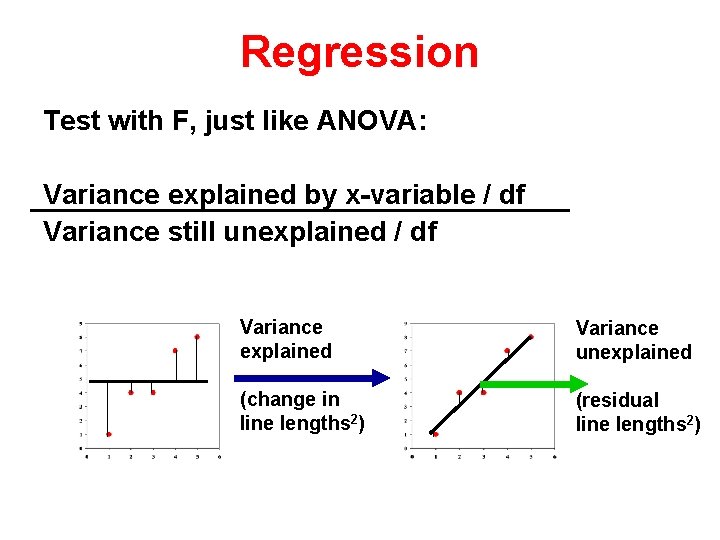
Regression Test with F, just like ANOVA: Variance explained by x-variable / df Variance still unexplained / df Variance explained Variance unexplained (change in line lengths 2) (residual line lengths 2)

Regression Test with F, just like ANOVA: Variance explained by x-variable / df Variance still unexplained / df In regression, each x-variable will normally have 1 df

Regression Test with F, just like ANOVA: Variance explained by x-variable / df Variance still unexplained / df Essentially a cost: benefit analysis – Is the benefit in variance explained worth the cost in using up degrees of freedom?

Regression example Total variance for 32 data points is 300 units. An x-variable is then regressed against the data, accounting for 150 units of variance. 1. What is the R 2? 2. What is the F ratio?

Regression example Total variance for 32 data points is 300 units. An x-variable is then regressed against the data, accounting for 150 units of variance. 1. What is the R 2? 2. What is the F ratio? R 2 = 150/300 = 0. 5 Why is df error = 30? F 1, 30 = 150/1 = 30 150/30
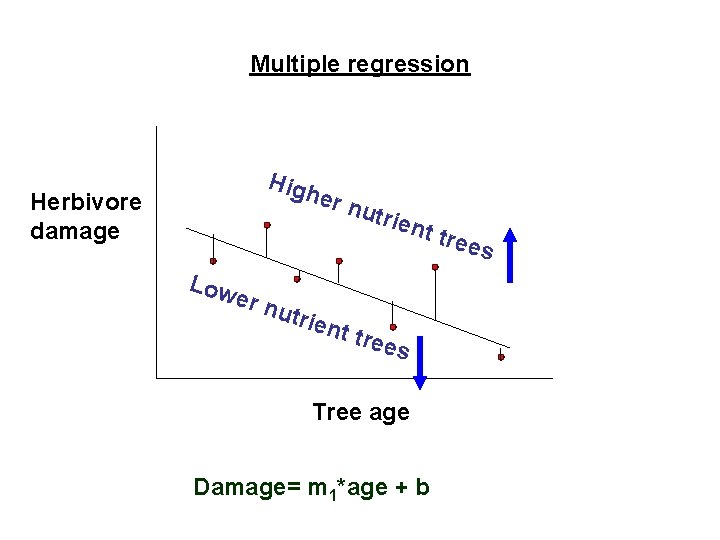
Multiple regression Herbivore damage High er n utrie nt tr e es Low er n utrie nt tr e es Tree age Damage= m 1*age + b
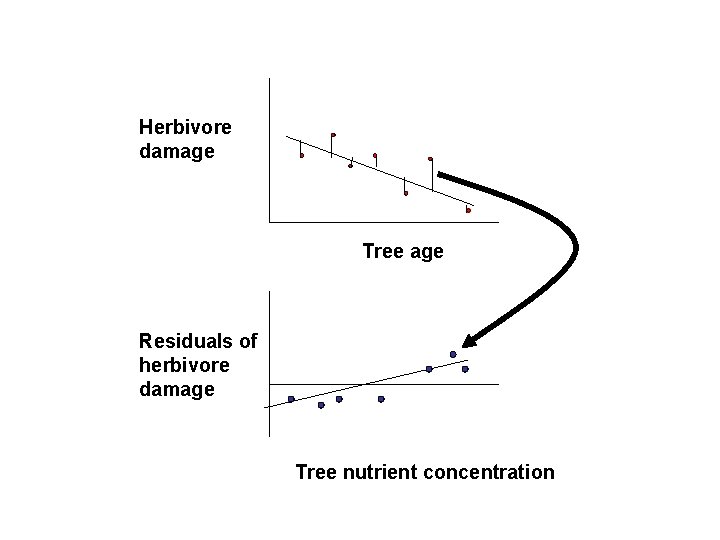
Herbivore damage Tree age Residuals of herbivore damage Tree nutrient concentration
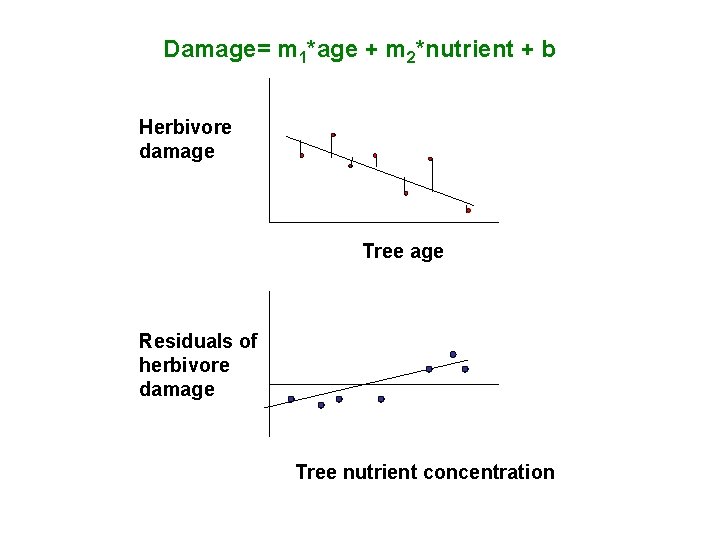
Damage= m 1*age + m 2*nutrient + b Herbivore damage Tree age Residuals of herbivore damage Tree nutrient concentration
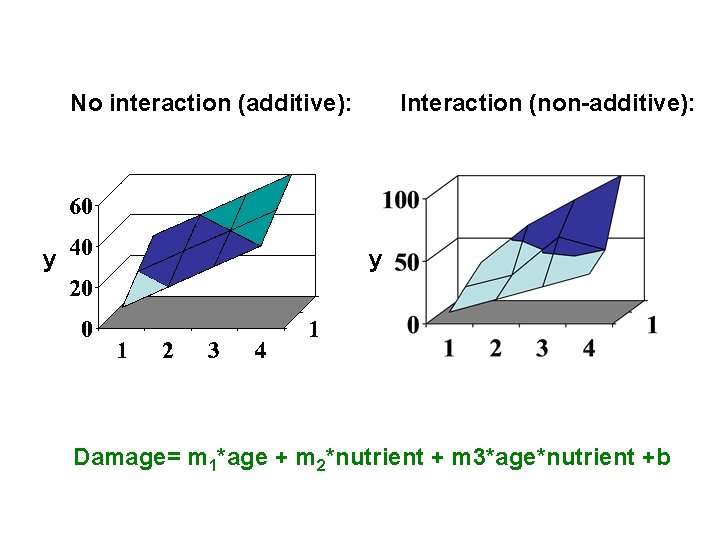
No interaction (additive): y Interaction (non-additive): y Damage= m 1*age + m 2*nutrient + m 3*age*nutrient +b

Non-linear regression? Just a special case of multiple regression! Y = m 1 x +m 2 x 2 +b Y = m 1 x 1 +m 2 x 2 +b XX 1 1 2 3 4 5 6 7 XX 22 1 4 9 16 25 36 49 Y 1. 1 2. 0 3. 6 3. 1 5. 2 6. 7 11. 3

STEPWISE REGRESSION

Jump height (how high ball can be raised off the ground) 8 9 10 11 Feet off ground Total SS = 11. 11
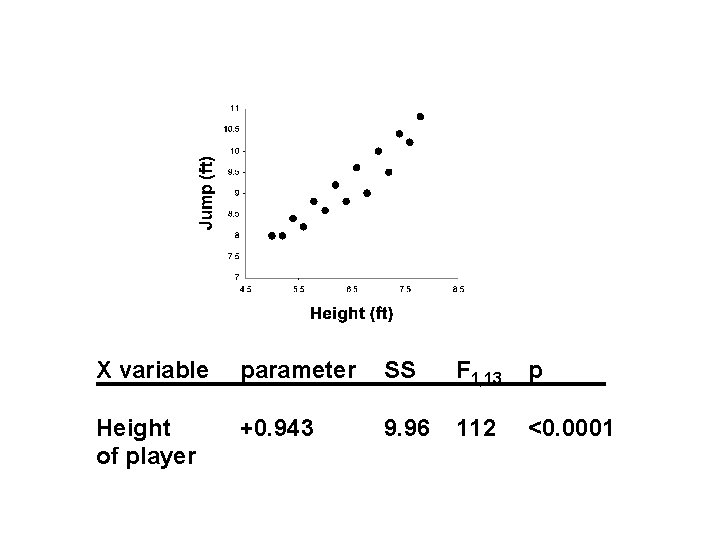
X variable parameter SS F 1, 13 p Height of player +0. 943 9. 96 112 <0. 0001
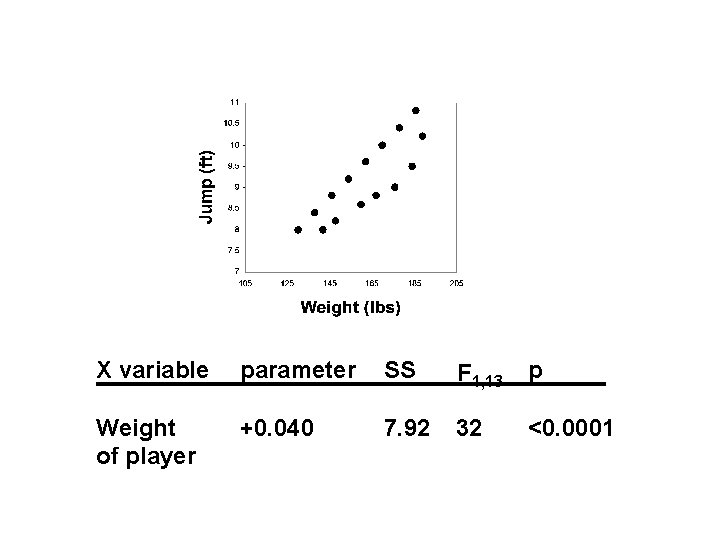
X variable parameter SS F 1, 13 p Weight of player +0. 040 7. 92 32 <0. 0001

Why do you think weight is + correlated with jump height?

An idea Perhaps if we took two people of identical height, the lighter one might actually jump higher? Excess weight may reduce ability to jump high…

How could we test this idea?
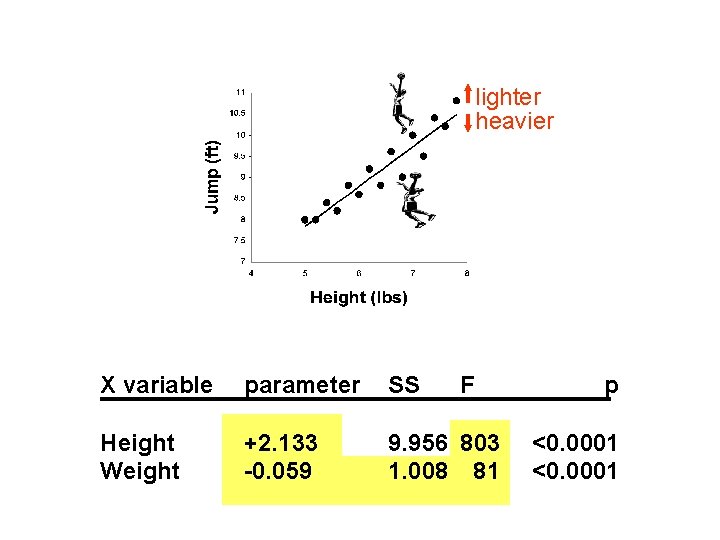
lighter heavier X variable parameter SS F Height Weight +2. 133 -0. 059 9. 956 803 1. 008 81 p <0. 0001

Questions: • Why did the parameter estimates change? • Why did the F tests change?
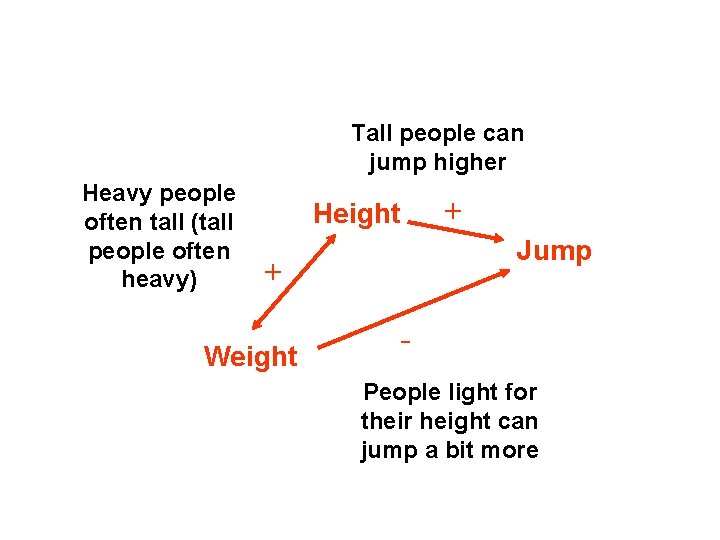
Tall people can jump higher Heavy people often tall (tall people often heavy) + Height Jump + Weight People light for their height can jump a bit more

The problem: The parameter estimate and significance of an x-variable is affected by the x-variables already in the model! How do we know which variables are significant, and which order to enter them in model?

Solutions 1) Use a logical order. For example in ANCOVA it makes sense to test the interaction first 2) Stepwise regression: “tries out” various orders of removing variables.

Stepwise regression Enters or removes variables in order of significance, checks after each step if the significance of other variables has changed Enters one by one: forward stepwise Enters all, removes one by one: backwards stepwise

Forward stepwise regression • Enter the variable with the highest correlation with y-variable first (p>p enter). • Next enter the variable to explains the most residual variation (p>p enter). • Remove variables that become insignificant (p> p leave) due to other variables being added. And so on…
- Slides: 28