Multiple Regression Analysis Part 2 Interpretation and Diagnostics

Multiple Regression Analysis: Part 2 Interpretation and Diagnostics 1

Learning Objectives n n n Understand regression coefficients and semi-partial correlations Learn to use diagnostics to locate problems with data (relative to MRA) Understand… q q q n n Assumptions Robustness Methods of dealing with violations Enhance our interpretation of equations Understand entry methods 2

Statistical Tests & Interpretation n Interpretation of regression coefficients q q q n Standardized Unstandardized Intercept Testing regression coefficients q q t-statistic & interpretation Testing R 2 3

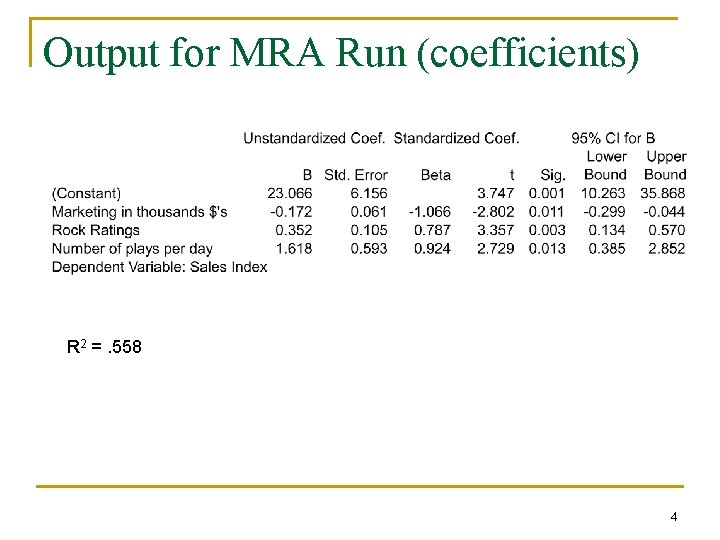
Output for MRA Run (coefficients) R 2 =. 558 4

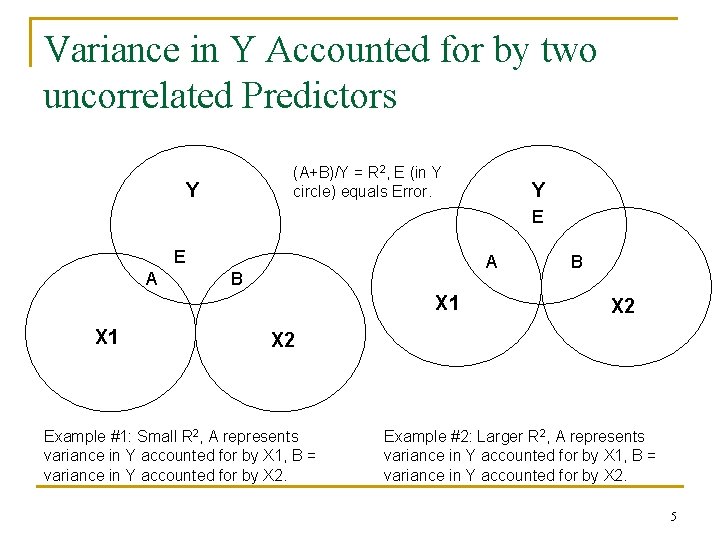
Variance in Y Accounted for by two uncorrelated Predictors (A+B)/Y = R 2, E (in Y circle) equals Error. Y Y E E A A B X 1 B X 2 Example #1: Small R 2, A represents variance in Y accounted for by X 1, B = variance in Y accounted for by X 2. Example #2: Larger R 2, A represents variance in Y accounted for by X 1, B = variance in Y accounted for by X 2. 5

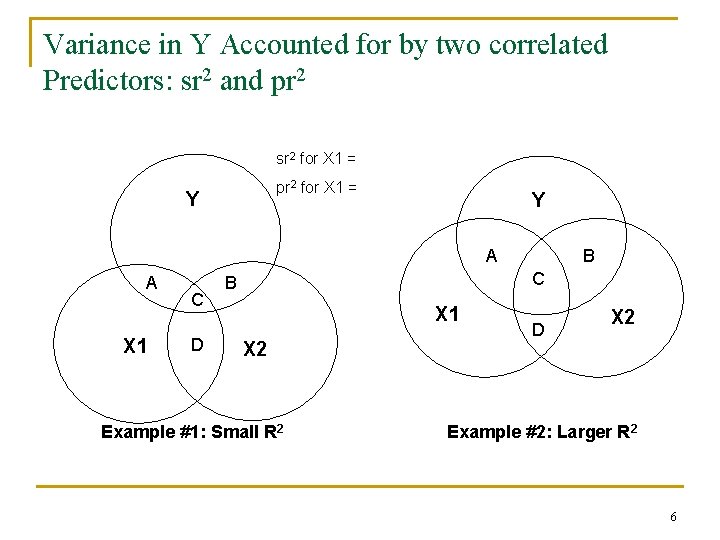
Variance in Y Accounted for by two correlated Predictors: sr 2 and pr 2 sr 2 for X 1 = pr 2 for X 1 = Y Y A A X 1 C D B C B X 1 X 2 Example #1: Small R 2 D X 2 Example #2: Larger R 2 6

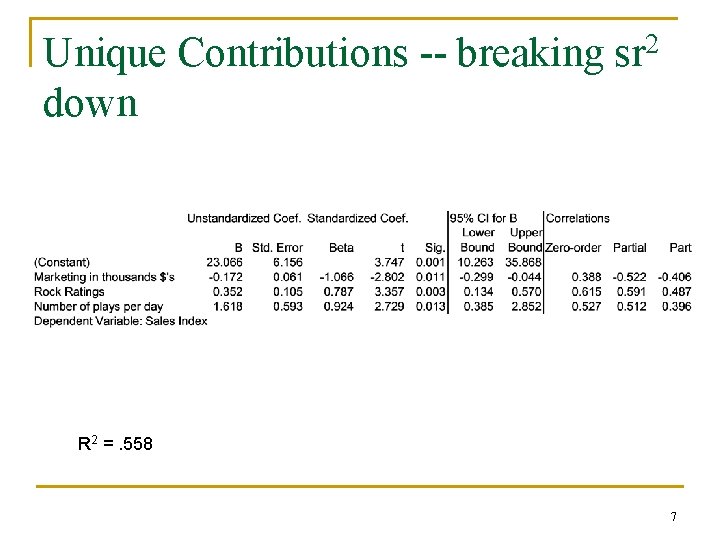
Unique Contributions -- breaking sr 2 down R 2 =. 558 7

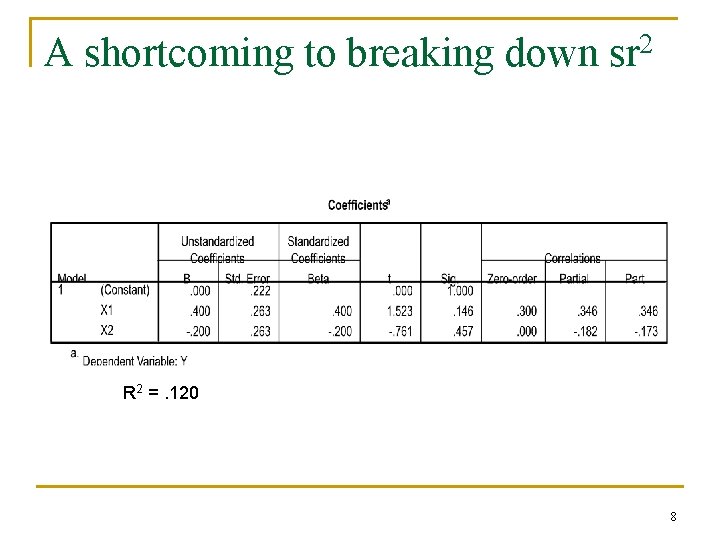
A shortcoming to breaking down sr 2 R 2 =. 120 8

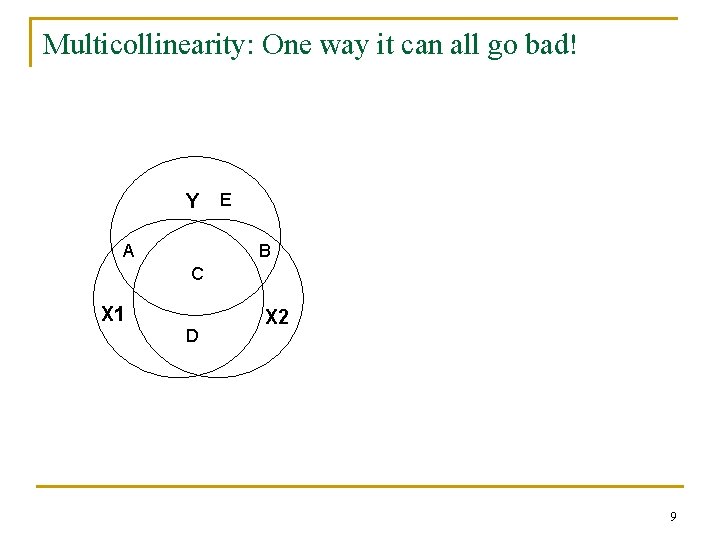
Multicollinearity: One way it can all go bad! Y A E B C X 1 D X 2 9

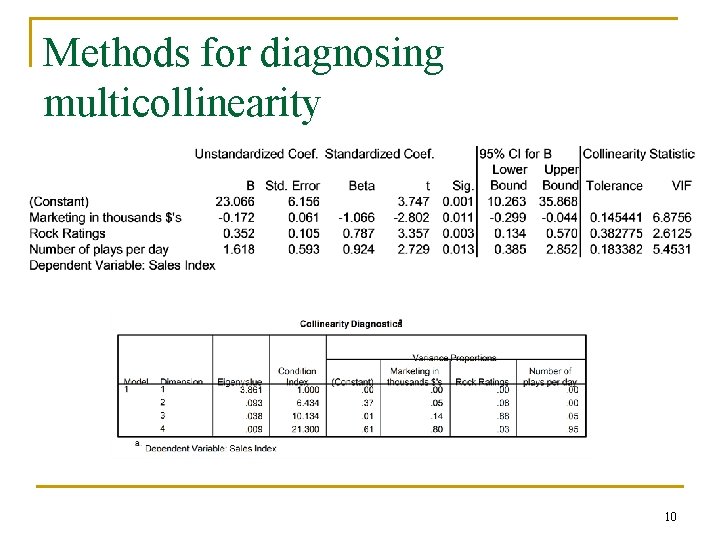
Methods for diagnosing multicollinearity 10

Ways to fix multicollinearity n n Discarding Predictors Combining Predictors q q n Using Principal Components Parcelling Ridge Regression 11

Outliers and Influential Observations: Another way it can all go bad! n Outliers on y n Outliers on x’s n Influential data points 12

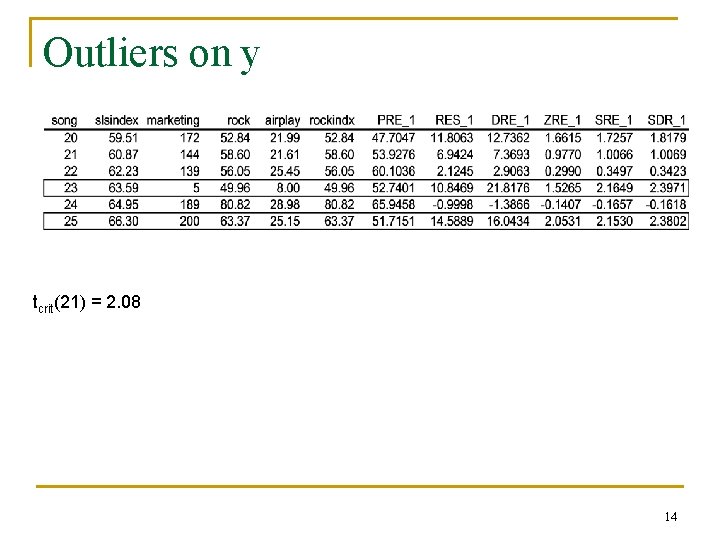
Outliers n Outliers on y q q q n Standardized Residuals Studentized Residuals (df = N – k – 1) Deleted Studentized Residuals Outliers on x’s q q Hat elements Mahalanobis Distance 13

Outliers on y tcrit(21) = 2. 08 14

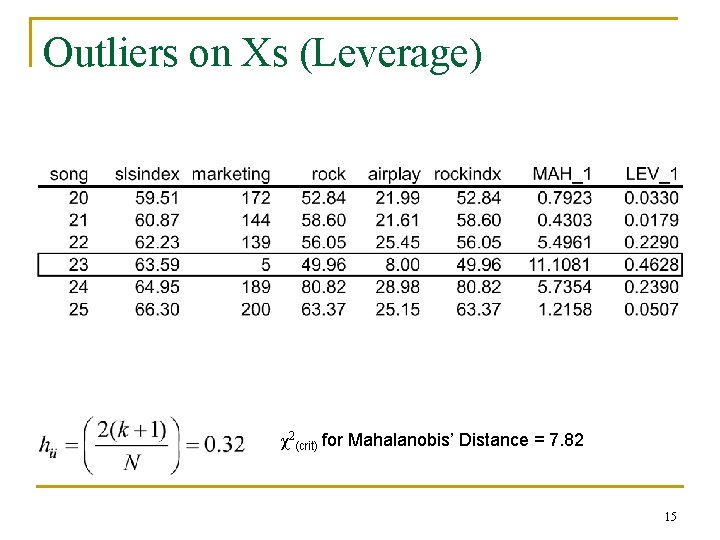
Outliers on Xs (Leverage) χ2(crit) for Mahalanobis’ Distance = 7. 82 15

Influential Observations n n Cook’s Distance (cutoff ≈ 1. 0) DFFITs [cut-offs of 2 or 2*((k+1)/n)0. 5] DFBeta Standardized DF Beta 16

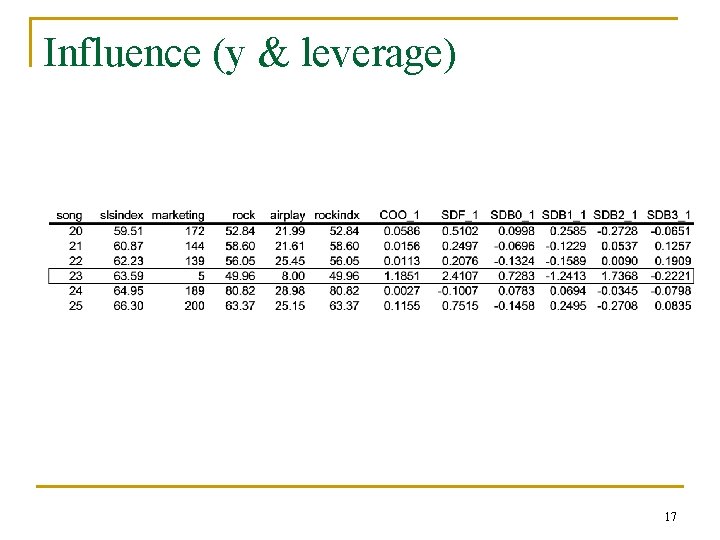
Influence (y & leverage) 17

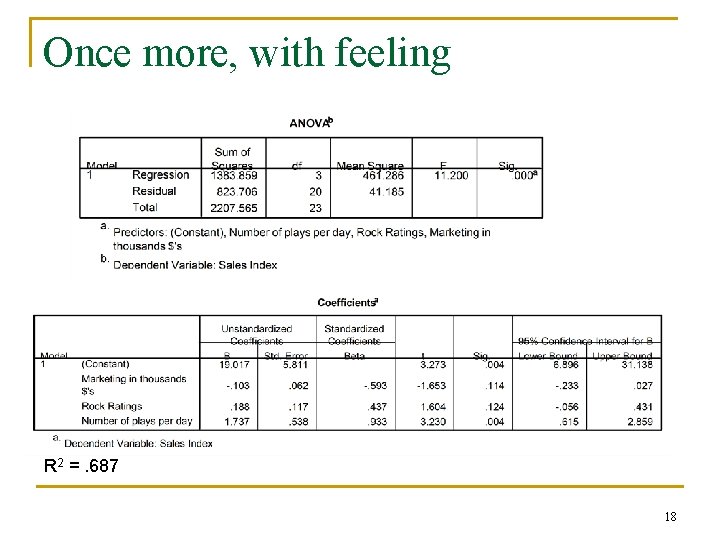
Once more, with feeling R 2 =. 687 18

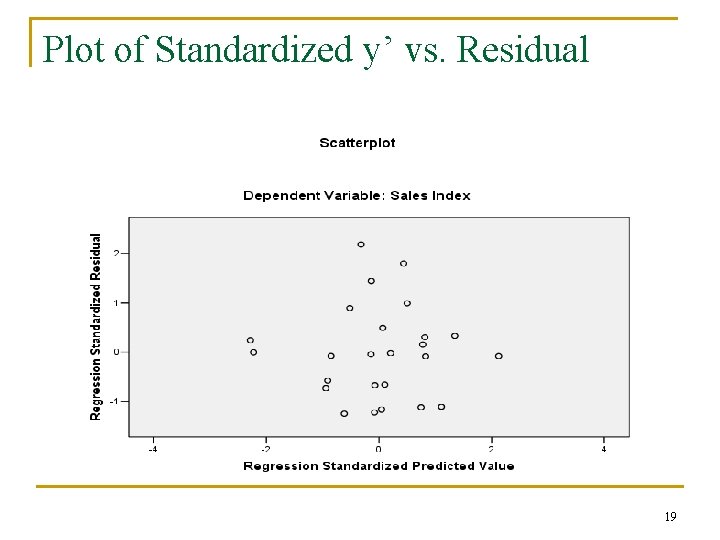
Plot of Standardized y’ vs. Residual 19

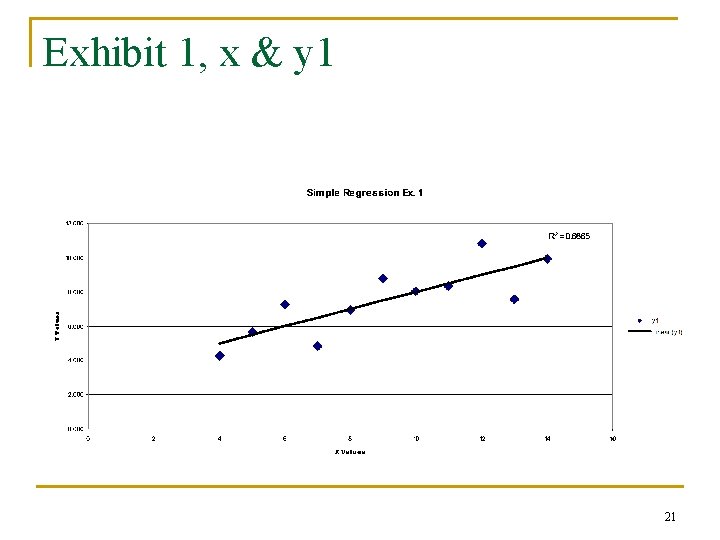
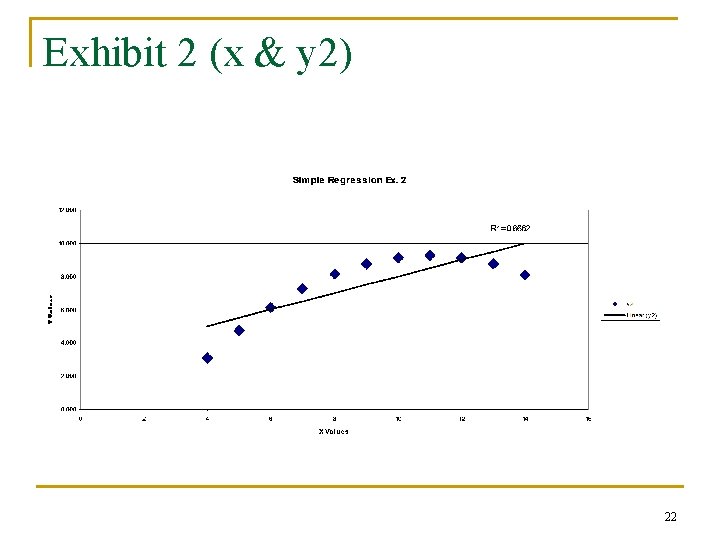
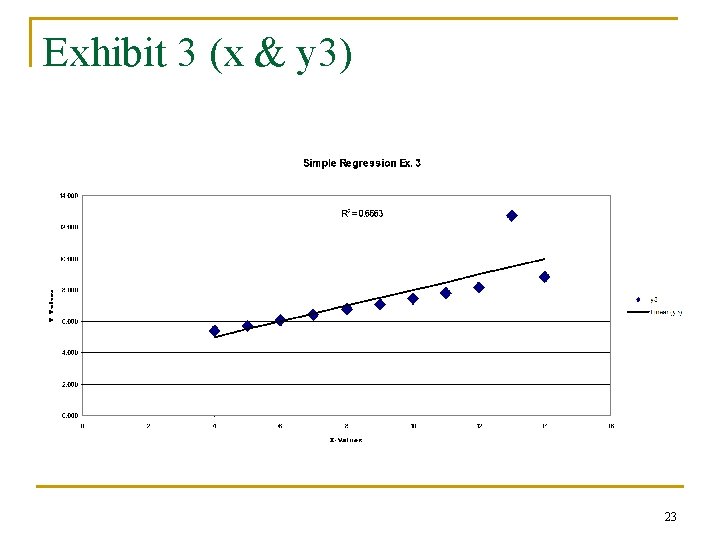
A cautionary tale: Some more ways it can all go bad! We will use X to predict y 1, y 2 and y 3 in turn. 20

Exhibit 1, x & y 1 21

Exhibit 2 (x & y 2) 22

Exhibit 3 (x & y 3) 23

Homoscadasticity: Yet another way it can all go bad! n What is homoscedasticity? q n n n Is it better to have heteroscedasticity? The effects of violation How to identify it Strategies for dealing with it 24

A visual representation of ways that it can all go bad! 25

Effect Size Multiple Correlation (R): SMC (R 2): 26

Cross Validation n Why n Useful statistics and techniques n Conditions under which likelihood of crossvalidation is increased 27

Assumptions of Regression n n n Sample Size Absence of Outliers & Influential Observations Absence of Multicollinearity and Singularity Normality Linearity Homoscedasticity of Errors Independence of Errors 28

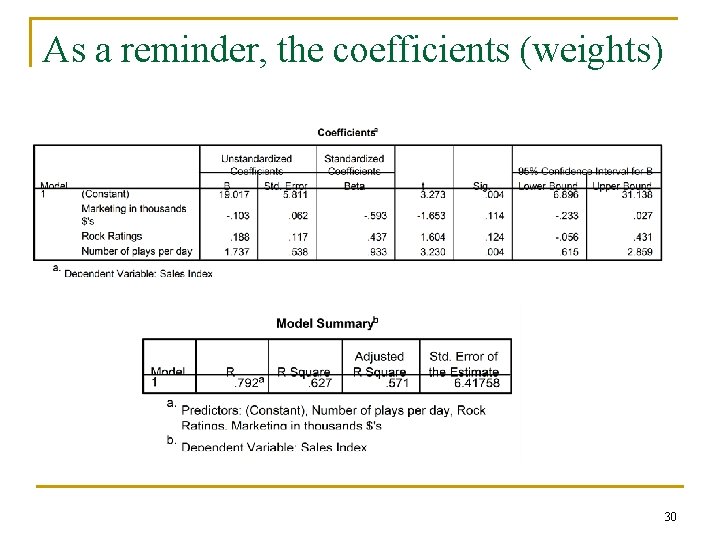
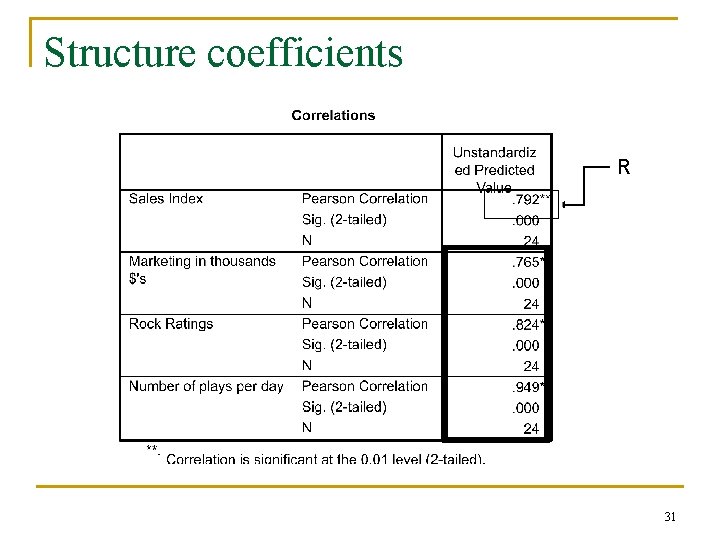
Structure Coefficients n What are they? q n n Vs. pattern coefficients or “weights” Why we may need both When they would be used in MRA Why they are not commonly used How you get them in SPSS q CD sales example 29

As a reminder, the coefficients (weights) 30

Structure coefficients R 31

Model Building in MRA: “Canned” procedures n Enter n Forward n Backward Selection (Deletion) n Stepwise n Hierarchical 32

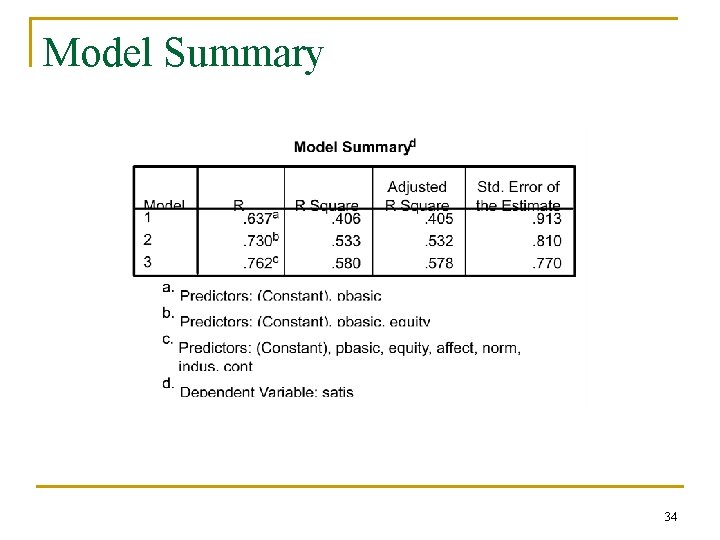
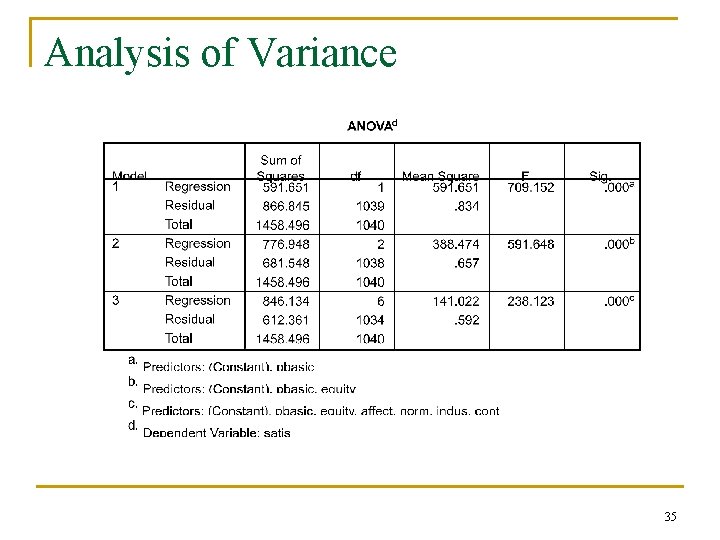
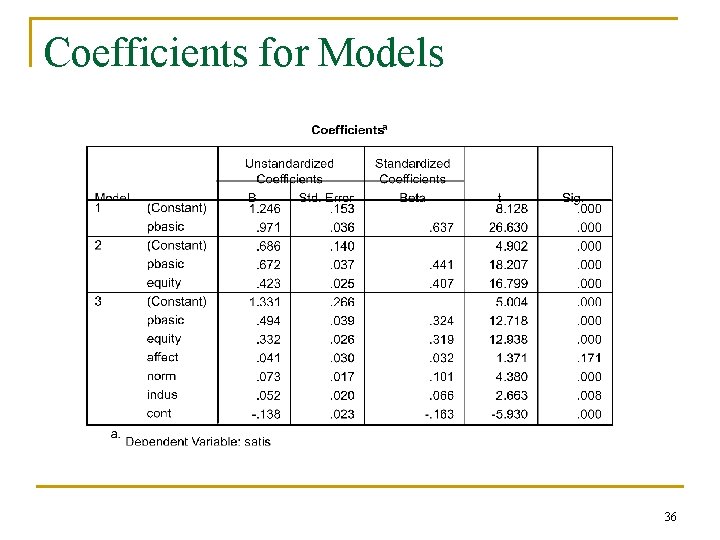
Hierarchical – Example Predict employee satisfaction n Block 1: “Hygiene Factor” n Block 2: “Equity” n Block 3: “Organizational Commitment” 33

Model Summary 34

Analysis of Variance 35

Coefficients for Models 36

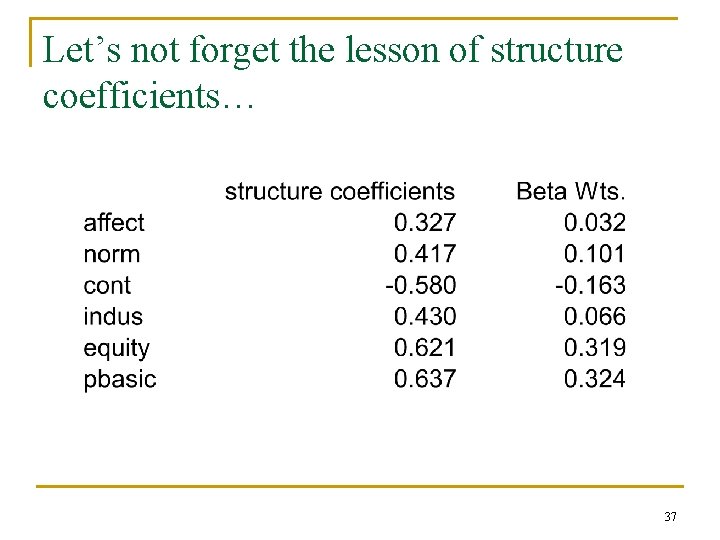
Let’s not forget the lesson of structure coefficients… 37

Interpretation revisited n n n n In light of multicollinearity Standardized or unstandardized? Suppressor effects Missing predictors Correlated / uncorrelated predictors Structure coefficients Reliability of indicators Mathematical maximization nature of MRA 38