Multiple Objective Decision Making Basic concepts General MODM

Multiple Objective Decision Making 王日昌. 資管. 長庚

Basic concepts • • General MODM model Dominated Efficient solutions Preference. . – Pre: (direct) nominal, ordinal, cardinal – Active…: direct, indirect – Post…: indirect

Decision space • x, y: decision variables, 決策變數、 可控手段 • Decision space: 決策 空間 (x, y: 2 dimension) • plot(0, 0, 7, 7); xlabel('x: 白天作業時數 '); ylabel('y: 夜間作業時數');

Constraints • Limited by resources? • Feasible region • Closed/opened region (x, y>=0) • Draw out: • x<=5 x=5, left • y<=5 y=5, lower • x+y<=7 – x=0, y=7 – y=0, x=7 – Left-lower

Closed feasible region • Find the crossed points: – – – • (0, 0): start point (5, 0) (5, 2) (2, 5) (0, 0): end point x=[0 5 5 2 0 0]; y=[0 0 2 5 5 0]; plot(x, y); xlabel('x: 白天作業時數'); ylabel('y: 夜間作業時 數');

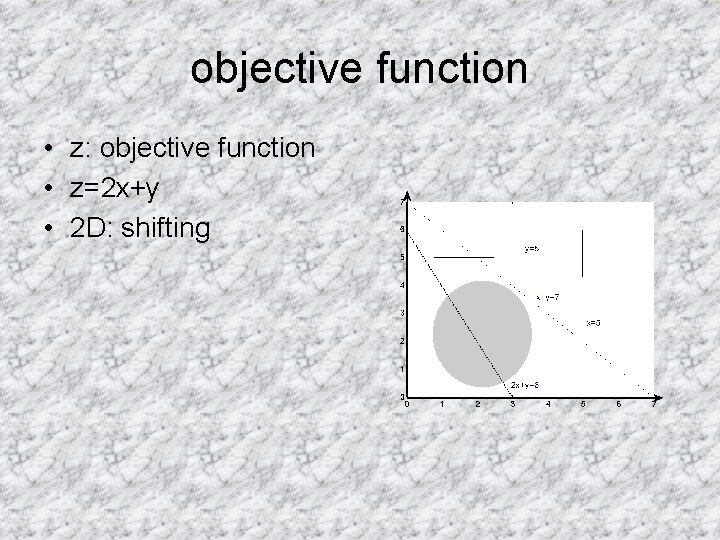
objective function • z: objective function • z=2 x+y • 2 D: shifting

3 D objective function • • Z: objective function Z=2 x+y 3 -dimension Find top point in restricted surface • [xx, yy]=meshgrid(0: 7); zz=2*xx+yy; meshc(xx , yy, zz); hold on; x=[0 5 5 2 0 0]; y=[0 0 2 5 5 0]; plot 3(x, y, [0 0 0 0], 'k'); plot 3(x, y, 2*x+y, 'k', 'Line. Width', 3);

[xx, yy]=meshgrid(0: . 2: 7); zz=zfun 1(xx, yy); meshz(xx, yy, zz); • edit zfun 1. m • • • • function z=zfun 1(x, y) [ttlx, ttly]=size(x); z=zeros(ttlx, ttly); for i=1: ttlx, for j=1: ttly, z(i, j)=2*x(i, j)+y(i, j); if x(i, j)<0, z(i, j)=0; end if y(i, j)<0, z(i, j)=0; end if x(i, j)>5, z(i, j)=0; end if y(i, j)>5, z(i, j)=0; end if x(i, j)+y(i, j)>7, z(i, j)=0; end end

2 objective functions • Multi-objective: more than one objective functions – Max z 1=2 x+y – Max z 2=-2 x+y • How to solve?

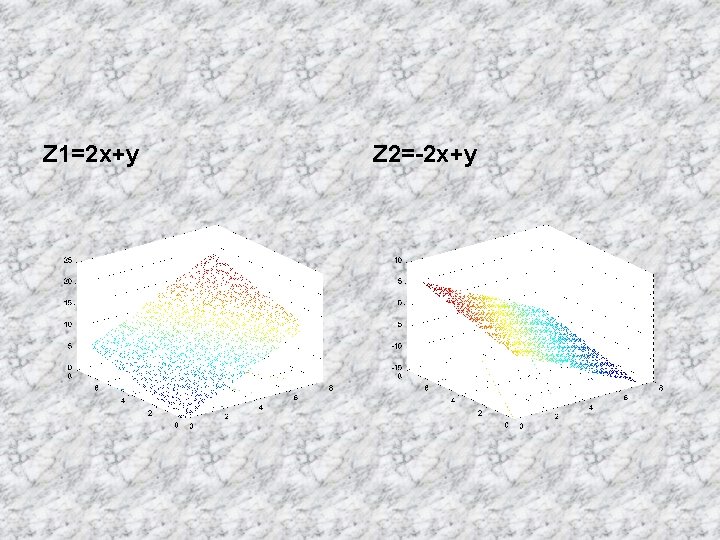
Z 1=2 x+y Z 2=-2 x+y

Linear transform

x=[0 5 5 2 0 0]; y=[0 0 2 5 5 0]; plot(x, y); xlabel('x'); ylabel('y'); x=[0 5 5 2 0 0]; y=[0 0 2 5 5 0]; z 1=2*x+y; z 2=-2*x+y; plot(z 1, z 2); xlabel('z 1'); ylabel('z 2');

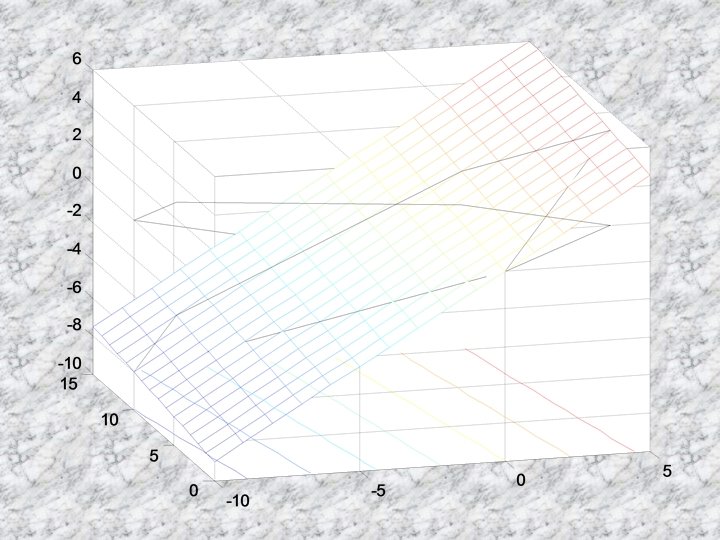
weighted • w 1 z 1+w 2 z 2 • w 1=0. 1, w 2=0. 9 • w 1=. 1; w 2=. 9; [z 1, z 2]=meshgrid(0: 15, -10: 5); meshc(z 1, z 2, w 1*z 1+w 2*z 2); hold on; x=[0 5 5 2 0 0]; y=[0 0 2 5 5 0]; z 1=2*x+y; z 2=2*x+y; plot 3(z 1, z 2, [0 0 0 0], 'k-'); plot 3(z 1, z 2, w 1*z 1+w 2*z 2, 'k');

Advanced methods • • Compromised Trade-off table Weighting method E-constraint MOLP GP STEM Fuzzy MOLP