Multiple Model approach to MultiParametric Model Predictive Control

Introduction ü with explicit solution the MPC is expanding its application area to low-level

Outline ü multi-parametric MPC ü tracking controller and offset removal ü case study plant

Model predictive controller, an MPC ü linear system defined by a SS model ü

Explicit solution of MPC ü u(k) = function of current state! ü PWA on

State controller -> Tracking contrl. ü offset-free reference tracking » velocity form augmentation ü

Process: pressure control in annealer ünonlinear high-order process, disturbances üactuators: • pump – slow

Process: nonlinear simulation model ü 2 nd order linear dynamics ü static input nonlinearities

Control design: hybrid PWA model ü augment the original linear model with data from

Control design: PWA process model ü gains for each local dynamical model defined in

Control design: tuning ücontroller parameter tuning • guide: reasonable computation time of controller •

Results: simulation studies ü MM mp-MPC (N=6, Nu=2) vs linear mp-MPC (N=6, Nu=2) ütracking

Results: simulation studies ü MM mp-MPC (N=27, Nu=2) vs linear mp-MPC (N=27, Nu=2) ü

Conclusions ü improved performance due do reduced plant-tomodel mismatch ü low computation demand &

Slides: 16

Download presentation

Multiple Model approach to Multi-Parametric Model Predictive Control of a Nonlinear Process a simulation case study Boštjan Pregelj, Samo Gerkšič Jožef Stefan Institute, Ljubljana, Slovenia bostjan. pregelj@ijs. si, samo. grerksic@ijs. si 10 th Ph. D Workshop on Systems and Control September 2009, Hluboka nad Vltavou, Czech Republic

Introduction ü with explicit solution the MPC is expanding its application area to low-level control • disturbance rejection • offset-free tracking • output feedback (states usually not measurable) » controller – estimator interplay • complexity (significant offline computation burden) ü hybrid mp-MPC methods • • control of hybrid or nonlinear systems hybrid estimator required controller and estimator model stitching/switching extremly demanding computation & complex partition ü multiple-model approach • simplified, suboptimal solution

Outline ü multi-parametric MPC ü tracking controller and offset removal ü case study plant • pressure control in wire annealer • nonlinear simulation model ü controller design • PWA process model • controller & Kalman filter tuning ü results ü remarks & conclusions

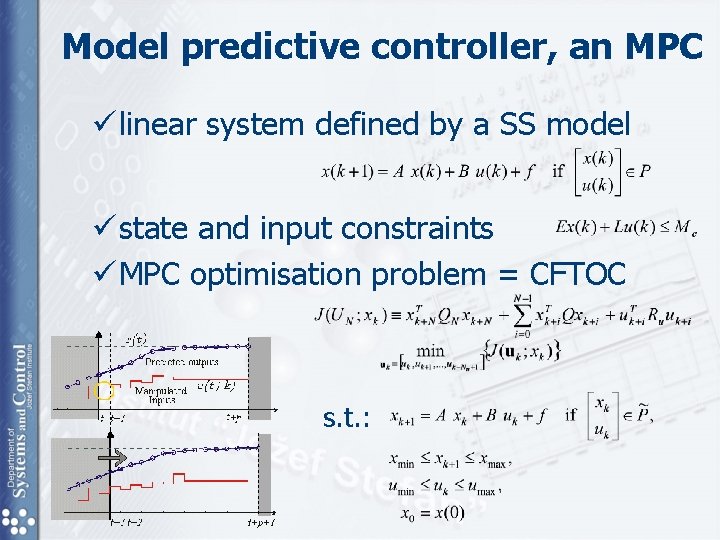
Model predictive controller, an MPC ü linear system defined by a SS model ü state and input constraints ü MPC optimisation problem = CFTOC s. t. :

Explicit solution of MPC ü u(k) = function of current state! ü PWA on polyhedra control law • where describes i -th region (polyhedron) ü properties: • regions have affine boundaries • value function J*k is convex, continuous, piecewise quadratic function of x(k), • optimizer: x*k is affine function of x(k), possibly discontinuous (at some types of boundaries)

State controller -> Tracking contrl. ü offset-free reference tracking » velocity form augmentation ü elimination of offset to disturbance due » tracking error integration » disturbance estimation ü output feedback » Kalman filter observer » additional integrating disturbance state d(k) » additional KF tuning possibilities > responce tuning with disturb. on states, inputs > input/output step disturbance model

Process: pressure control in annealer ünonlinear high-order process, disturbances üactuators: • pump – slow response, large operating range • valve – fast response, small operating range ütwo input single output constrained system • additional DOF • constraints 0 < u 1 < 50 [s-1], 0 < u 2 < 100 [%], -2 -5 < Δu 1 < 5 [s ], -50 < Δu 2 < 50 [%/s]. 0 < p < 133 [mbar]

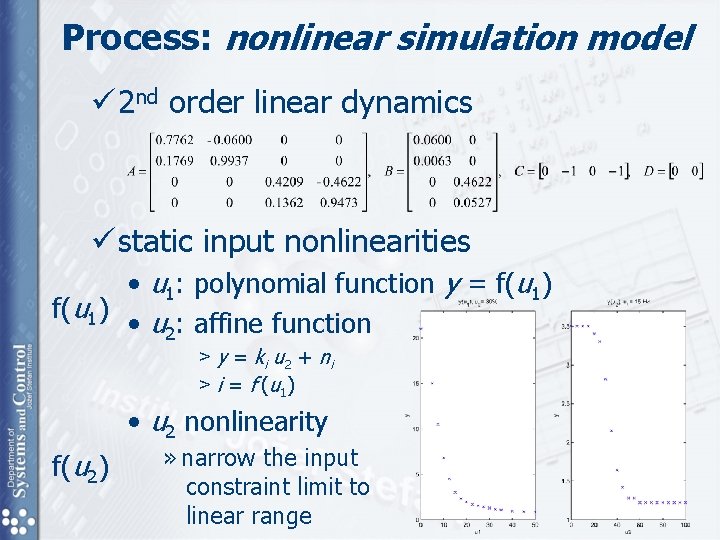
Process: nonlinear simulation model ü 2 nd order linear dynamics ü static input nonlinearities • u 1: polynomial function y = f(u 1) • u 2: affine function > y = ki u 2 + n i > i = f ( u 1 ) • u 2 nonlinearity f(u 2) » narrow the input constraint limit to linear range

Control design: hybrid PWA model ü augment the original linear model with data from other operating points OP u 1 [HZ] u 2 [%] u 1 gain u 2 gain 1 (low extreme) 15 30 -0. 3203 -1. 0057 2 (high extreme) 10 30 -1. 0010 -2. 4136 3 (intermediate) 12. 5 30 -0. 7007 -1. 7096 ü model switching » f(x 2) » f(x 2, x 4) boundary lines:

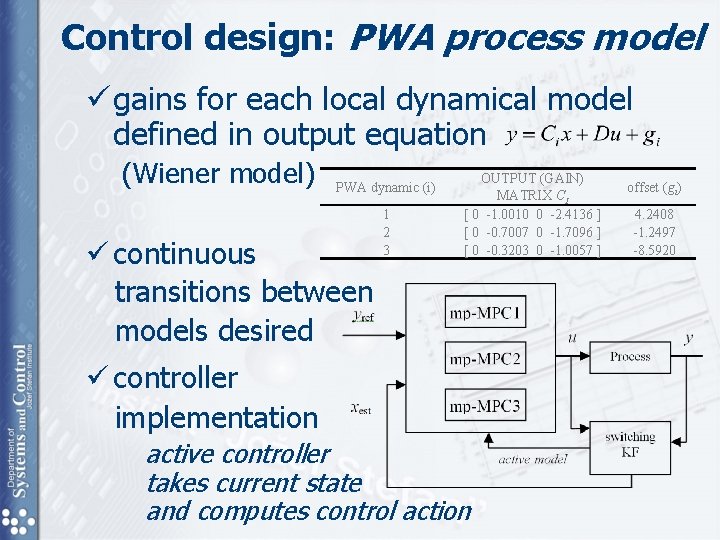
Control design: PWA process model ü gains for each local dynamical model defined in output equation (Wiener model) PWA dynamic (i) ü continuous transitions between models desired 1 2 3 OUTPUT (GAIN) MATRIX CI [ 0 -1. 0010 0 -2. 4136 ] [ 0 -0. 7007 0 -1. 7096 ] [ 0 -0. 3203 0 -1. 0057 ] ü controller implementation active controller takes current state and computes control action offset (gi) 4. 2408 -1. 2497 -8. 5920

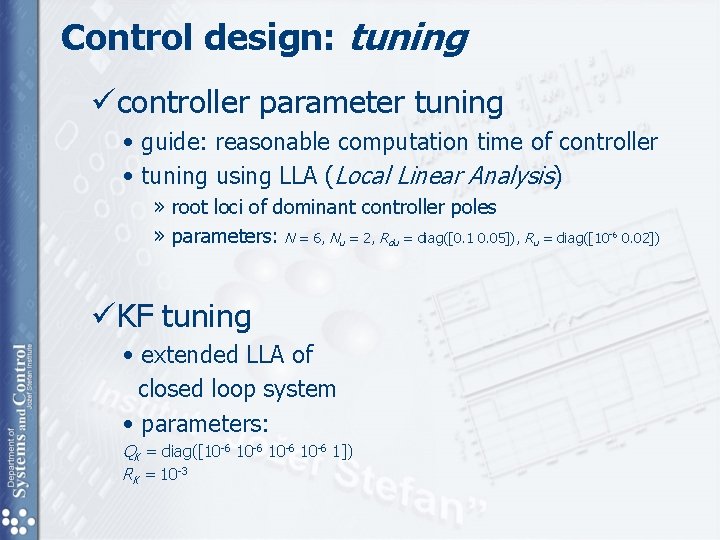
Control design: tuning ücontroller parameter tuning • guide: reasonable computation time of controller • tuning using LLA (Local Linear Analysis) » root loci of dominant controller poles » parameters: N = 6, Nu = 2, Rdu = diag([0. 1 0. 05]), Ru = diag([10 -6 0. 02]) üKF tuning • extended LLA of closed loop system • parameters: QK = diag([10 -6 1]) RK = 10 -3

Results: simulation studies ü MM mp-MPC (N=6, Nu=2) vs linear mp-MPC (N=6, Nu=2) ütracking reference signal steps along three local dynamical models) ülinear model (black) from intermediate OP ücontroller partition composed of 3 x 100 reg. (hybrid mp-MPC 200 k)

Results: simulation studies ü MM mp-MPC (N=27, Nu=2) vs linear mp-MPC (N=27, Nu=2) ü improved performance due to longer horizons. ücontroller resuling in ~3 x 300 regions ühybrid mp-MPC not really feasible

Conclusions ü improved performance due do reduced plant-tomodel mismatch ü low computation demand & complexity ü emphasis to nonlinear PWA plane matching ü suboptimal solution • controller does not anticipate switch in prediction • controller sellection via scheduling variable ü better results achievable • other suboptimal approaches (current & future work) » simplified hybrid mp-MPC » restrict switching among dynamics in prediction » keeps higher level of optimality

Thank you!