Multiple Linear Regression Polynomial Regression Monotonic but NonLinear

Multiple Linear Regression Polynomial Regression

Monotonic but Non-Linear • The relationship between X and Y may be monotonic but not linear. • The linear model can be tweaked to take this into account by applying a monotonic transformation to Y, X, or both X and Y. • Predicting calories consumed from number of persons present at the meal.

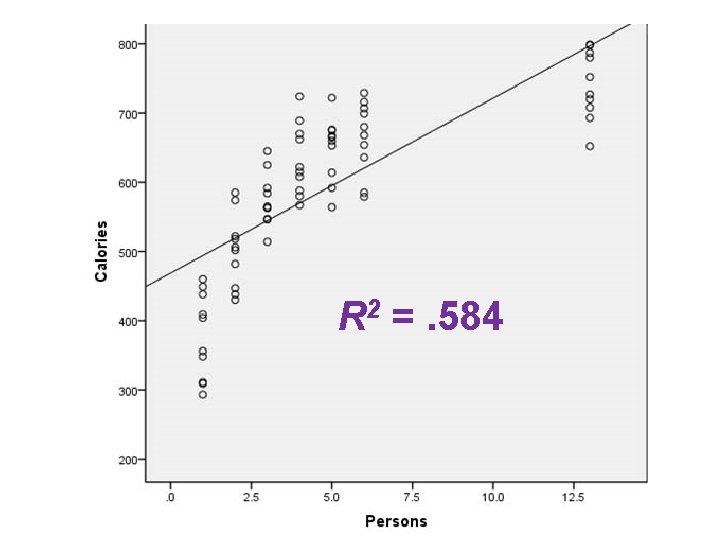
R 2 =. 584

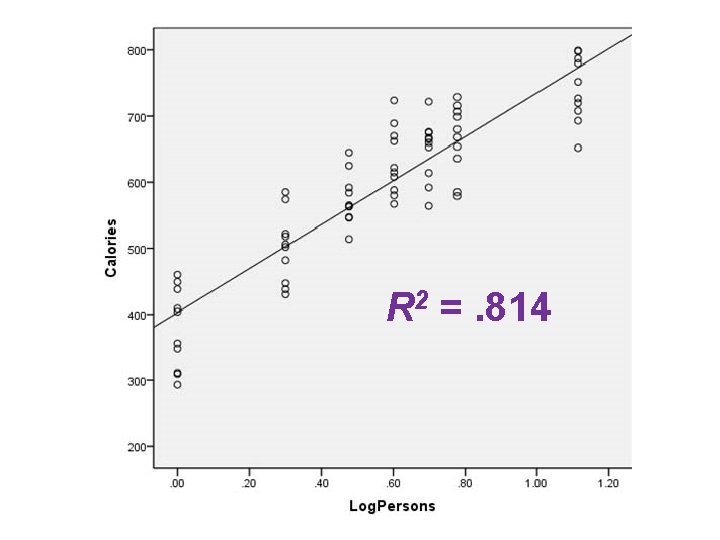
R 2 =. 814

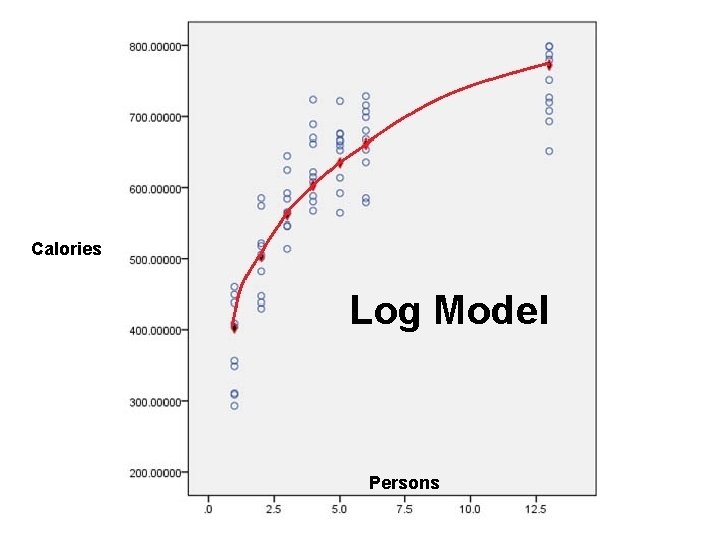
Calories Log Model Persons

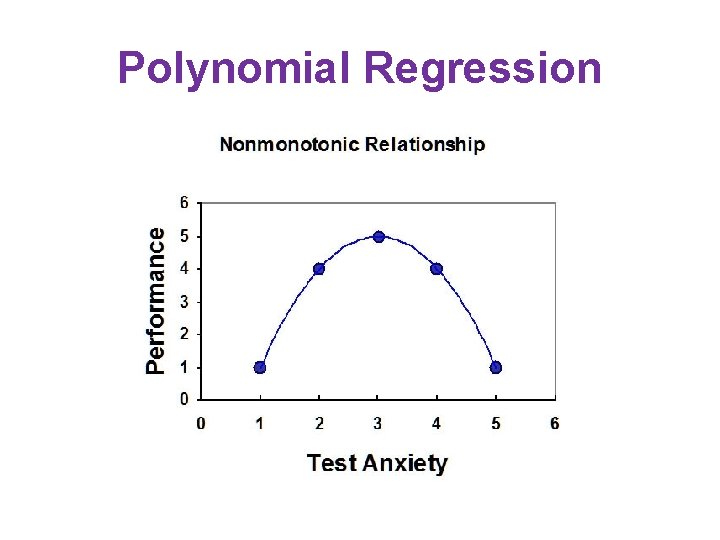
Polynomial Regression

• A monotonic transformation will not help here. • A polynomial regression will. • Copp, N. H. Animal Behavior, 31, 424 -430 • Subjects = containers, each with 100 ladybugs • Containers lighted on one side, dark on the other • Y = number on the lighted side • X = temperature

Polynomial Models • Quadratic: • Cubic: • For each additional power of X added to the model, the regression line will have one more bend.

Using Copp’s Data • Compute Temp 2, Temp 3 and Temp 4. • Conduct a sequential multiple regression analysis, entering Temp first, then Temp 2, then Temp 3, and then Temp 4. • At each step, evaluate whether or not the last entered predictor should be retained.

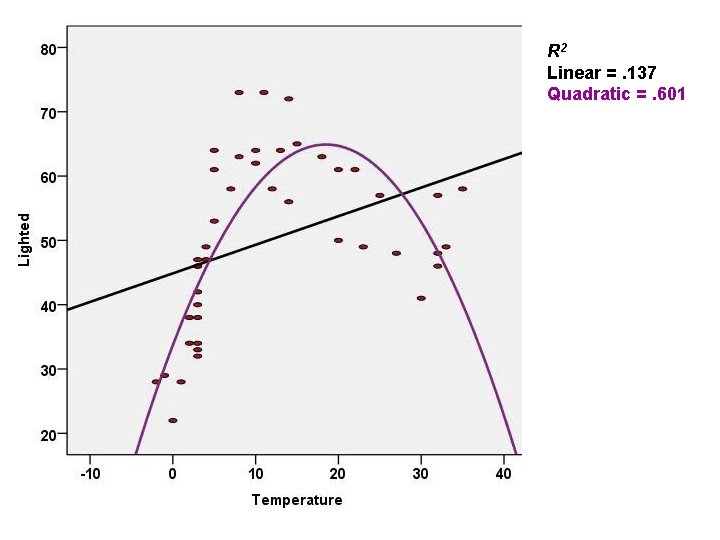
R 2 Linear =. 137 Quadratic =. 601

The Quadratic Model • The quadratic model clearly fits the data better than does the linear model. • Phototaxis is positive as temps rise to about 18 and negative thereafter.

A Cubic Model • R 2 has increased significantly, from. 601 to. 753, p <. 001 • Does an increase of 15. 2% of the variance justify making the model more complex? • I think so.

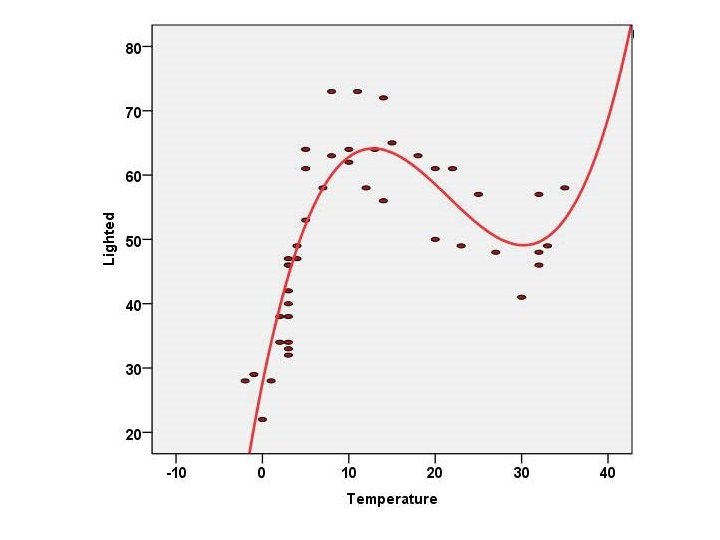
Interpretation • Ladybugs buried in leaf mold in Winter head up, towards light, as temperatures warm. • With warming beyond 12, head for some shade – the aphids are in the shade under Karl’s tomato plant leaves. • With warming beyond 32, this place is too hot, lets get out of here.

A Quartic Model • R 2 =. 029, p =. 030 • Does this small increase in R 2 justify making the model more complex? • Can you make sense of a third bend in the curve.

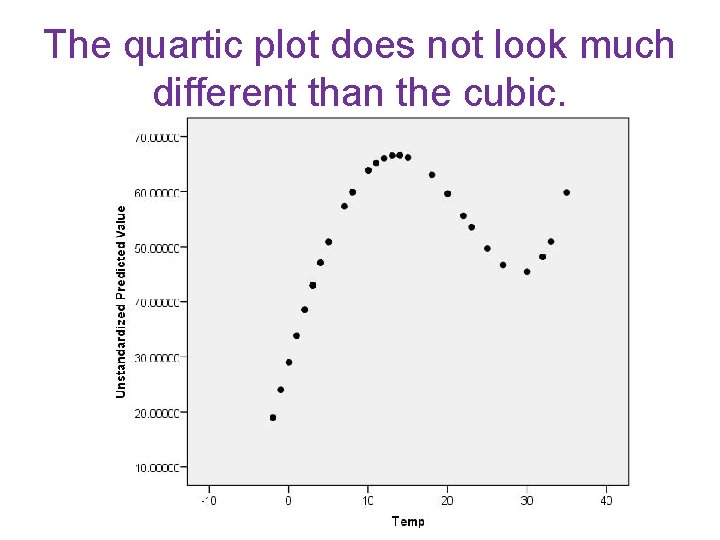
The quartic plot does not look much different than the cubic.

Multicollinearity • May be a problem whenever you have products or powers of predictors in the model. • Center the predictor variables, • Or simply standardize all variables to mean 0, standard deviation 1.

• For complete SPSS output, go here • Polynomial regression can also be used to conduct ANOVA.