Multiple Linear Regression Partial Regression Coefficients bi is

Multiple Linear Regression Partial Regression Coefficients

bi is an Unstandardized Partial Slope • • Predict Y from X 2 Predict X 1 from X 2 Predict from That is, predict the part of Y that is not related to X 2 from the part of X 1 that is not related to X 2 • The resulting b is that for b 1 in

Øbi is the average change in Y per unit change in Xi with all other predictor variables held constant

is a Standardized Partial Slope • • Predict ZY from Z 2 Predict Z 1 from Z 2 Predict from The slope of the resulting regression is 1. • 1 is the number of standard deviations that Y changes per standard deviation change in X 1 after we have removed the effect of X 2 from both X 1 and Y

R 2 • Can be interpreted as a simple r 2, a proportion of variance explained.

• Unless R 2 = 1, the variance in the predicted Y scores is less than the variance in the actual Y scores. • What is this phenomenon called?

Regression Towards the Mean

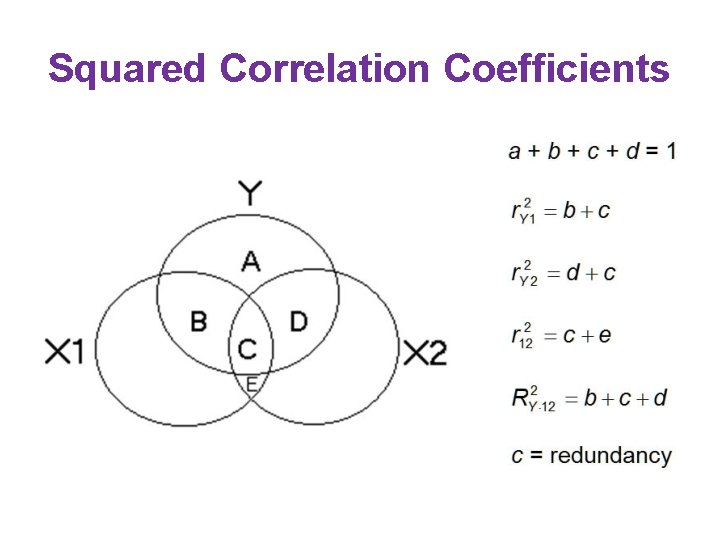
Squared Correlation Coefficients

Squared Semipartial Correlation • the proportion of all the variance in Y that is associated with one predictor but not with any of the other predictors. • the decrease in R 2 that results from removing a predictor from the model

sri • Predict X 1 from X 2 • • sri is the simple correlation between ALL of Y and that part of X 1 that is not related to any of the other predictors

Squared Partial Correlation • Of the variance in Y that is not associated with any other predictors, what proportion is associated with the variance in Xi

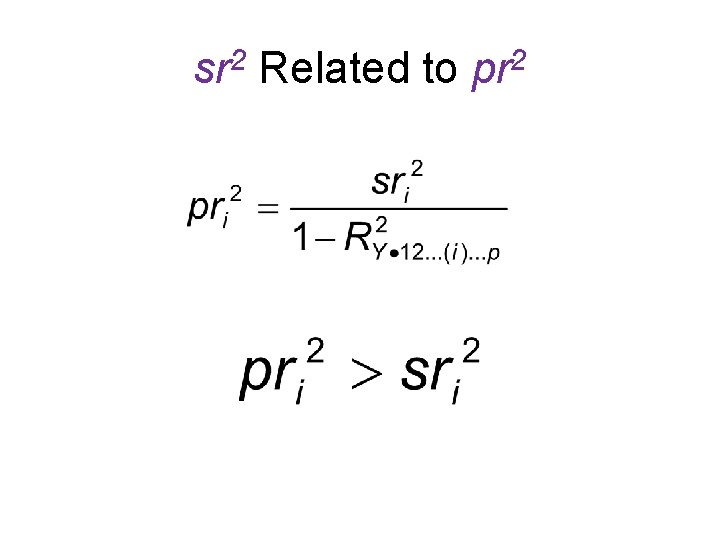
sr 2 Related to pr 2

pri • Predict Y from X 2 • Predict X 1 from X 2 • • is the r between Y partialled for all other predictors and Xi partialled for all other predictors.

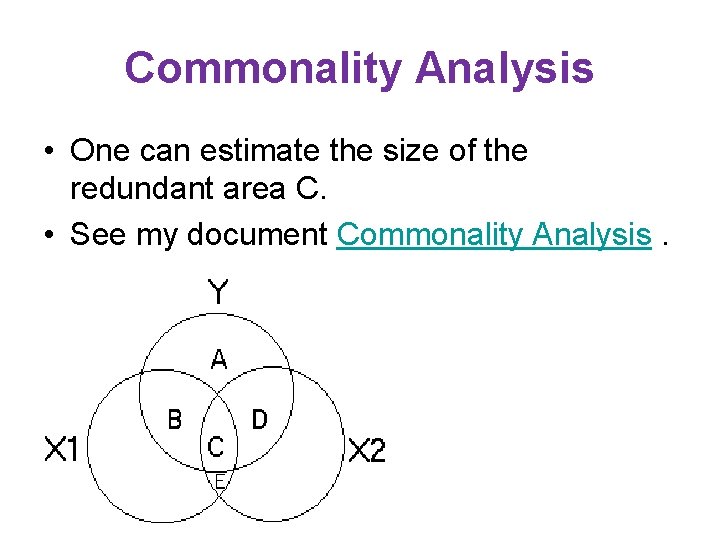
Commonality Analysis • One can estimate the size of the redundant area C. • See my document Commonality Analysis.

A Demonstration Ø Partial. sas – run this SAS program to obtain an illustration of the partial nature of the coefficients obtained in a multiple regression analysis.

More Details Ø Multiple R 2 and Partial Correlation/Regression Coefficients

Relative Weights Analysis • Partial regression coefficients exclude variance that is shared among predictors. • It is possible to have a large R 2 but none of the predictors have substantial partial coefficients. • There are now methods by which one can partition the R 2 into pseudo-orthogonal portions, each portion representing the relative contribution of one predictor variable.

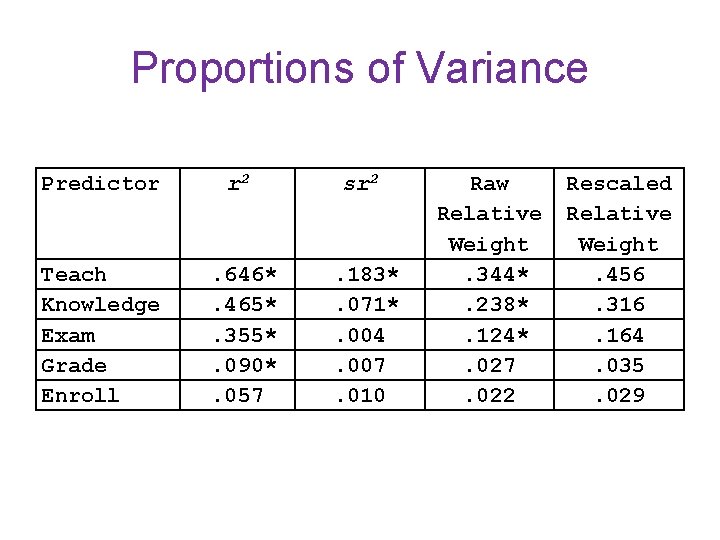
Proportions of Variance Predictor r 2 sr 2 Teach Knowledge Exam Grade Enroll . 646*. 465*. 355*. 090*. 057 . 183*. 071*. 004. 007. 010 Raw Relative Weight. 344*. 238*. 124*. 027. 022 Rescaled Relative Weight. 456. 316. 164. 035. 029

• If the predictors were orthogonal, the sum of r 2 would be equal to R 2, and • The values of r 2 would be identical to the values of sr 2. • The sr 2 here is. 275, and R 2 =. 755, so • . 755 -. 275 = 48% of the variance in Overall is excluded from the squared semipartials due to redundancy.

Notice That • The sum of the raw relative weights =. 755 = the value of R 2. • The sum of the rescaled relative weights is 100%. • The sr 2 for Exam is not significant, but its raw relative weight is significant.