Multiple Comparisons Multiple Comparisons v Multiple Range Tests

Multiple Comparisons

Multiple Comparisons v. Multiple Range Tests ØTukey’s and Duncan’s v. Orthogonal Contrasts

Orthogonal Contrasts

AOV Orthogonal Contrasts

Tukey’s Multiple Range Test

Consider that cultivars A and B were developed in Idaho and C and D developed in California v Do the two Idaho cultivars have the same yield potential? v Do the two California cultivars have the same yield potential? v Are Idaho cultivars higher yielding than California cultivars?

Analysis of Variance

Orthogonality ci = 0 [c 1 i x c 2 i] = 0 -1 -1 +1 +1 -- ci = 0 -1 +1 -- ci = 0 +1 -1 -1 +1 -- ci = 0

Calculating Orthogonal Contrasts d. f. (single contrast) = 1 S. Sq(contrast) = M. Sq = [ ci x Yi]2/n ci 2]

Orthogonal Contrasts - Example

S. Sq = [ ci x Yi]/[n 2 ci ] S. Sq(1) [(-1)64. 1+(-1)76. 6+(1)40. 1+(1)47. 8]2/ n ci 2 = 52. 82/(3 x 4) = 232. 32

S. Sq(2) [(-1)x 64. 1+(+1) x 76. 6]2/(3 x 2) 26. 04 S. Sq(3) [(-1)x 40. 1+(+1)x 47. 8]2/(3 x 2) 9. 88

Orthogonal Contrasts

Orthogonal Contrasts v Five dry bean cultivars (A, B, C, D, and E). v Cultivars A and B are drought susceptible. v Cultivars C, D and E are drought resistant. v Four Replicate RCB, one location v Limited irrigation applied.

Analysis of Variance

Orthogonal Contrast Example #2 Tukey’s Multiple Range Test

Orthogonal Contrasts v Is there any difference in yield potential between drought resistant and susceptible cultivars? v Is there any difference in yield potential between the two drought susceptible cultivars? v Are there any differences in yield potential between the three drought resistant cultivars?

Orthogonal Contrasts

S. Sq(1)= [(-3)130+(-3)124+(2)141+(2)186+(2)119]2 /n ci 2 1302/(4 x 40) = 140. 8 S. Sq(2)= [(-1)130+(+1)124]2 /n ci 2 62/(4 x 2) = 4. 5 S. Sq(Rem) = S. Sq(Cult)-S. Sq(1)-S. Sq(2) 728. 2 -140. 8 -4. 5 = 582. 9 (with 2 d. f. )

Analysis of Variance

Partition Contrast(rem)

Analysis of Variance

Alternative Contrasts

S. Sq(1)= [(-3)130+(-3)124+(2)141+(2)186+(2)119]2 /n ci 2 1302/(4 x 40) = 140. 8 S. Sq(2)= [(-1)130+(-1)124+(-1)141+(4)186+(-1)119]2 /n ci 2 2302/(4 x 20) = 661. 2 S. Sq(Rem) = S. Sq(Cult)-S. Sq(1)-S. Sq(2) 728. 2 -140. 8 -661. 2 = -73. 8 (Oops !!!) (with 2 d. f. )

Orthogonality c 1 i = 0 ( c 2 i = 0 ( [c 1 i x c 2 i] = 0 (- -3) + (+2) = 0 = -1) + (-1) + (+4) + (-1) = 0 = 3)(-1)+(-3)(-1)+2(4)+2(-1) =10 =

More Appropriate Contrasts

Analysis of Variance

Conclusions v Almost all the variation between cultivars is accounted for by the difference between cv ‘D’ and the others. v The remaining 4 cultivars are not significantly different. v Orthogonal contrast result is exactly the same are the result from Tukey’s contrasts.

Conclusions v Important to make the “correct” orthogonal contrasts. v Important to make contrasts which have “biological sense”. v Orthogonal contrasts should be decided prior to analyses and not dependant on the data.

Orthogonal Contrasts v Four Brassica species (B. napus, B. rapa, B. juncea, and S. alba). v Ten cultivars ‘nested’ within each species. v Three insecticide treatments (Thiodan, Furidan, no insecticide). v Three replicate split-plot design.

Analysis of Variance

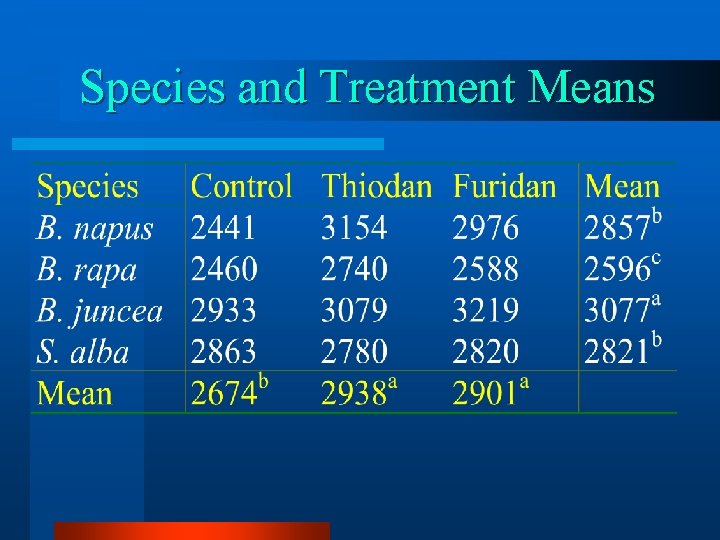
Species and Treatment Means

Orthogonal Contrasts

Orthogonal Contrasts

Analysis of Variance

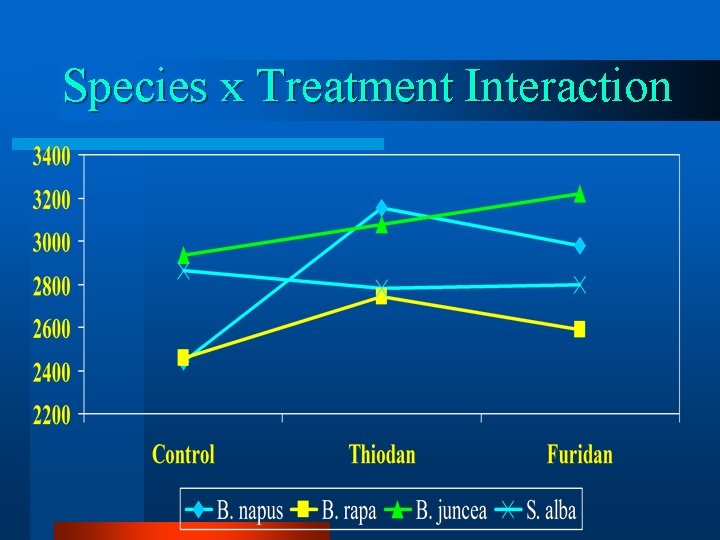
Species x Treatment Interaction

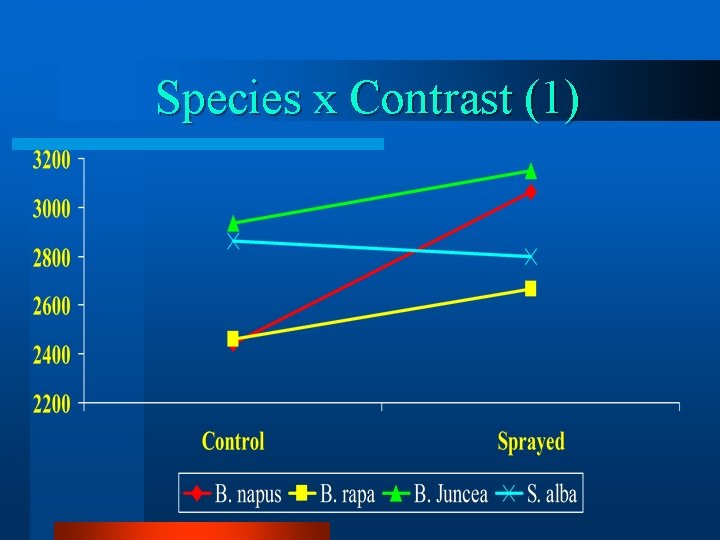
Species x Contrast (1)

Species x Contrast (2)

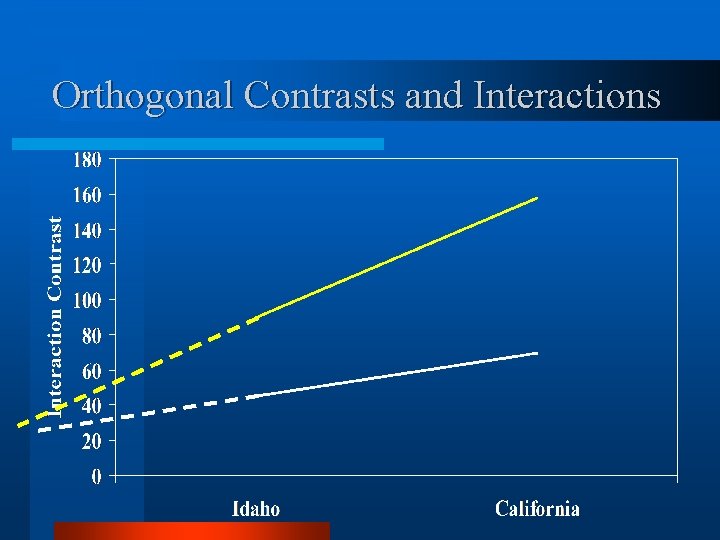
Orthogonal Contrasts and Interactions v Consider a cross classified factorial design with 4 replicates. v Four cultivars; 2 from Idaho and 2 from California (again). v 3 herbicide treatments; No-treatment control, Killall, and Onllik.

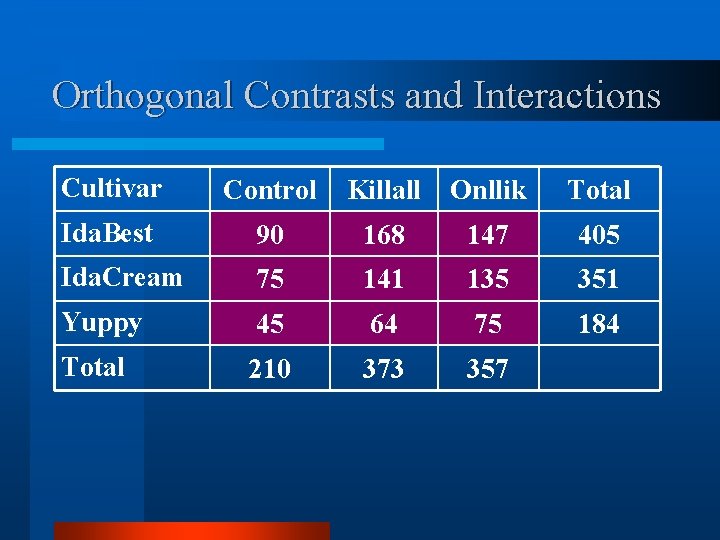
Orthogonal Contrasts and Interactions Cultivar Control Killall Onllik Total Ida. Best 90 168 147 405 Ida. Cream 75 141 135 351 Yuppy 45 64 75 184 Total 210 373 357

Orthogonal Contrasts and Interactions v Contrasts for cultivars? v. Idaho v California (-1 -1 +2), v. SS(Id v CA) = 2, 787; v Contrast for herbicides? v. Herbicide v No-treatment control (-2 +1 +1), v. SS(Herb v Not) = 1, 779; v Contrast for the interaction between the first two contrasts?

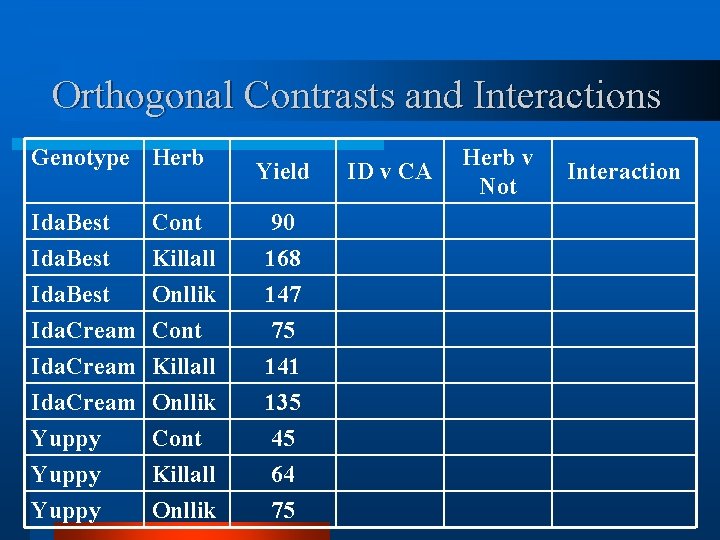
Orthogonal Contrasts and Interactions Genotype Herb Yield Ida. Best Cont 90 Ida. Best Killall 168 Ida. Best Onllik 147 Ida. Cream Cont 75 Ida. Cream Killall 141 Ida. Cream Onllik 135 Yuppy Cont 45 Yuppy Killall 64 Yuppy Onllik 75 ID v CA Herb v Not Interaction

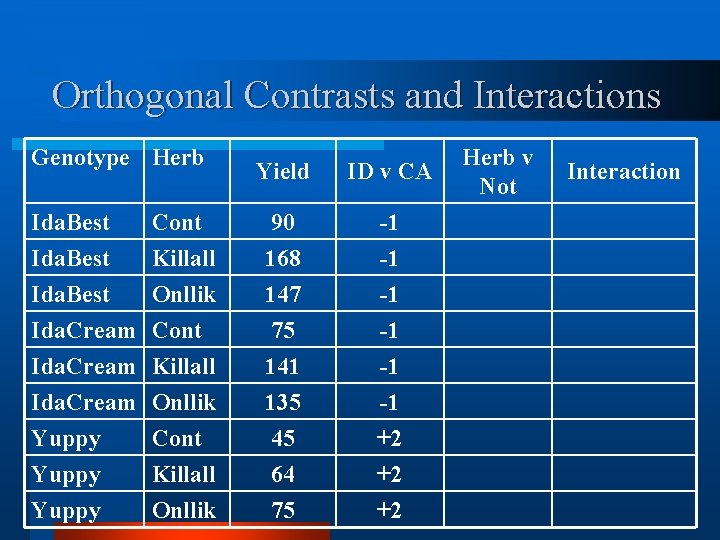
Orthogonal Contrasts and Interactions Genotype Herb Yield ID v CA Ida. Best Cont 90 -1 Ida. Best Killall 168 -1 Ida. Best Onllik 147 -1 Ida. Cream Cont 75 -1 Ida. Cream Killall 141 -1 Ida. Cream Onllik 135 -1 Yuppy Cont 45 +2 Yuppy Killall 64 +2 Yuppy Onllik 75 +2 Herb v Not Interaction

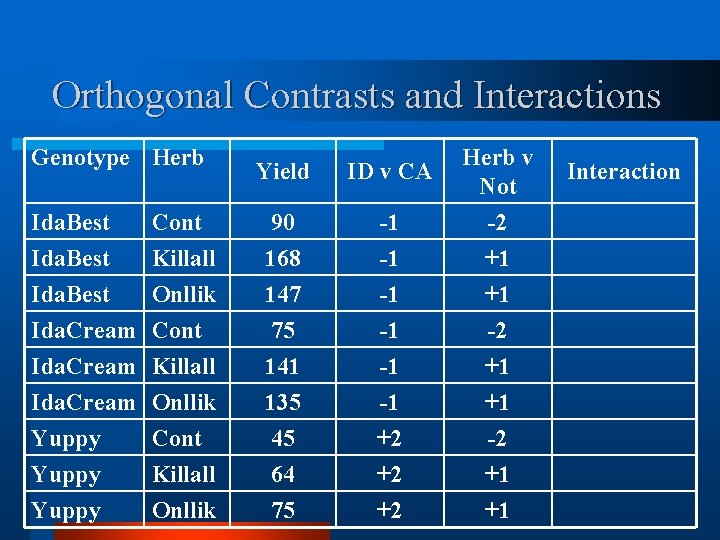
Orthogonal Contrasts and Interactions Genotype Herb Yield ID v CA Herb v Not Ida. Best Cont 90 -1 -2 Ida. Best Killall 168 -1 +1 Ida. Best Onllik 147 -1 +1 Ida. Cream Cont 75 -1 -2 Ida. Cream Killall 141 -1 +1 Ida. Cream Onllik 135 -1 +1 Yuppy Cont 45 +2 -2 Yuppy Killall 64 +2 +1 Yuppy Onllik 75 +2 +1 Interaction

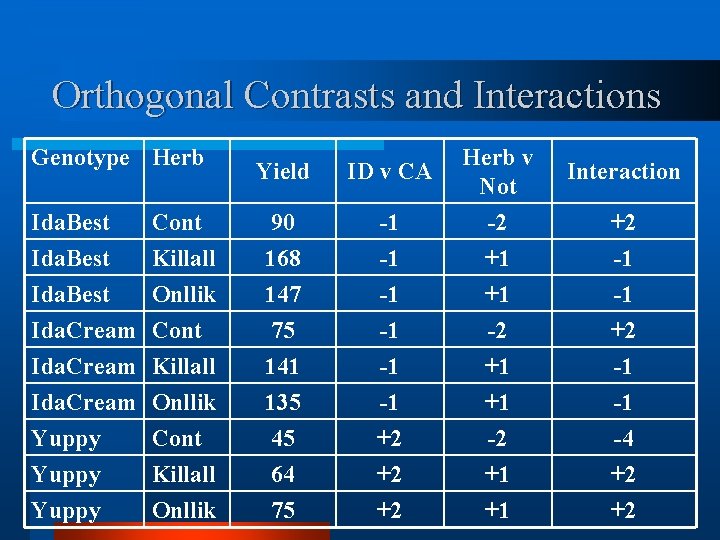
Orthogonal Contrasts and Interactions Genotype Herb Yield ID v CA Herb v Not Interaction Ida. Best Cont 90 -1 -2 +2 Ida. Best Killall 168 -1 +1 -1 Ida. Best Onllik 147 -1 +1 -1 Ida. Cream Cont 75 -1 -2 +2 Ida. Cream Killall 141 -1 +1 -1 Ida. Cream Onllik 135 -1 +1 -1 Yuppy Cont 45 +2 -2 -4 Yuppy Killall 64 +2 +1 +2 Yuppy Onllik 75 +2 +1 +2

Orthogonal Contrasts and Interactions v Contrasts for cultivars? v. Idaho v California (-1 -1 +2), v. SS(Id v CA) = 2, 787; v Contrast for herbicides? v. Herbicide v No-treatment control (-2 +1 +1), v. SS(Herb v Not) = 1, 779; v Contrast for the interaction between the first two contrasts? v. SS (Interaction) = 246.

Orthogonal Contrasts and Interactions

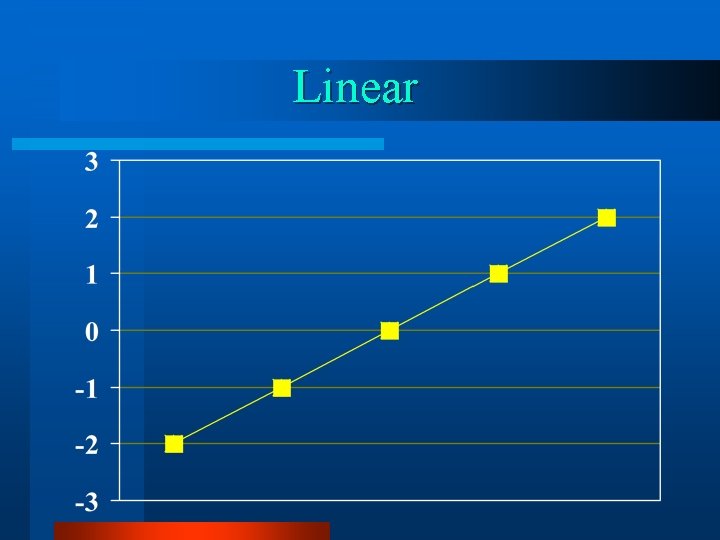
More Orthogonal Contrasts … Trend Analyses

Aim of Analyses of Variance v Detect significant differences between treatment means. v Determine trends that may exist as a result of varying specific factor levels.

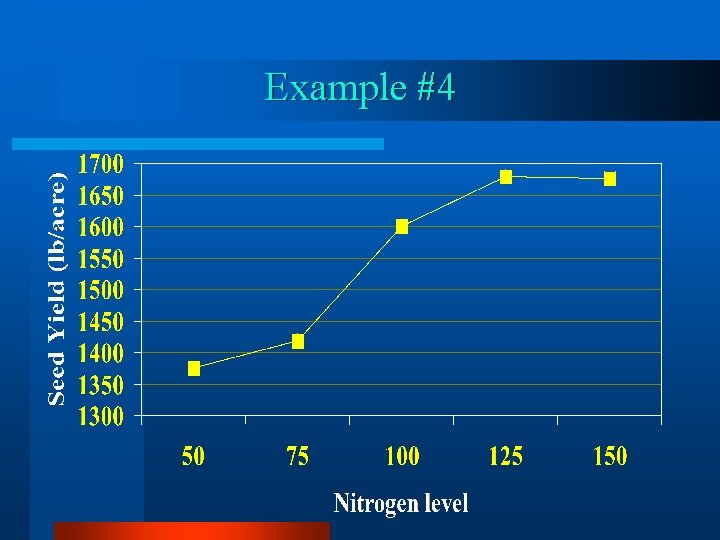
Example #4 v Ten yellow mustard (S. alba) cultivars. v Five different nitrogen application rates (50, 75, 100, 125, and 150)

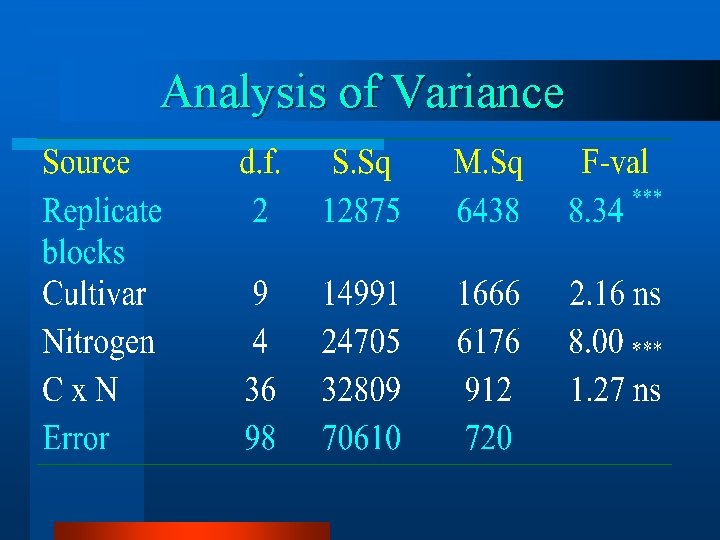
Analysis of Variance

Orthogonal Contrasts

Example #4

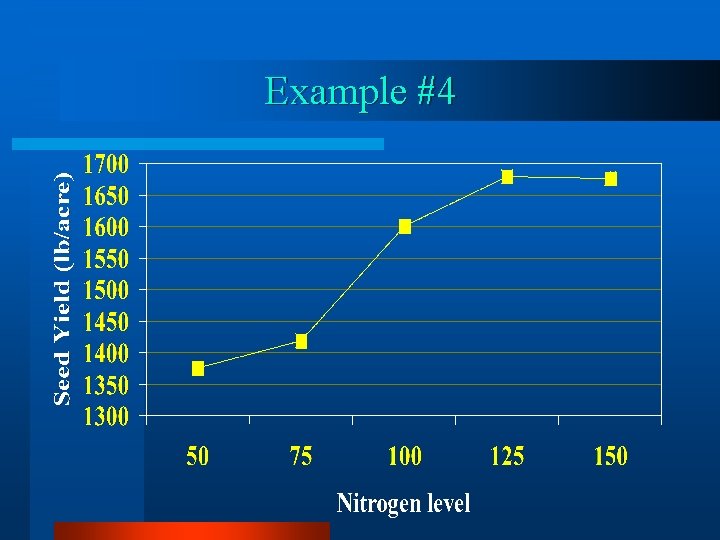
Example #4

Example #4

Analysis of Variance

Trend Analyses v. The F-value associates with a trend contrast is significant. v. All higher order trend contrasts are not significant.

Example #4

Linear

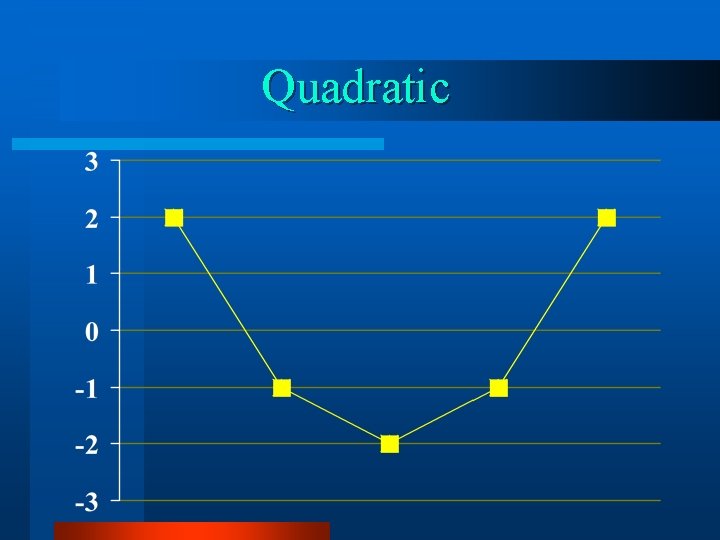
Quadratic

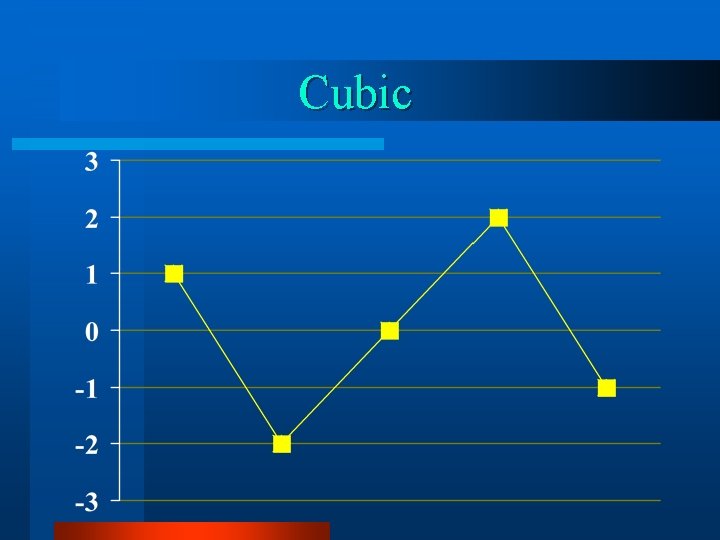
Cubic

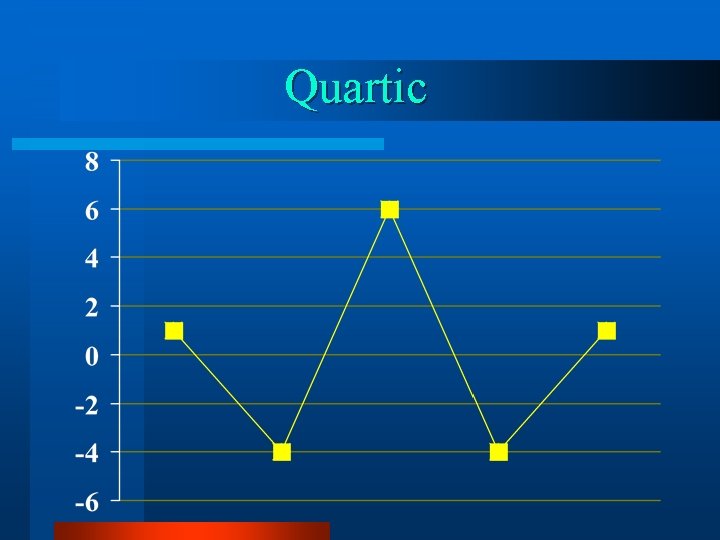
Quartic

Example #5 v. Two carrot cultivars (‘Orange Gold’ and ‘Bugs Delight’. v. Four seeding rates (1. 5, 2. 0, 2. 5 and 3. 0 lb/acre). v. Three replicates.

Example #5

Analysis of Variance

Analysis of Variance

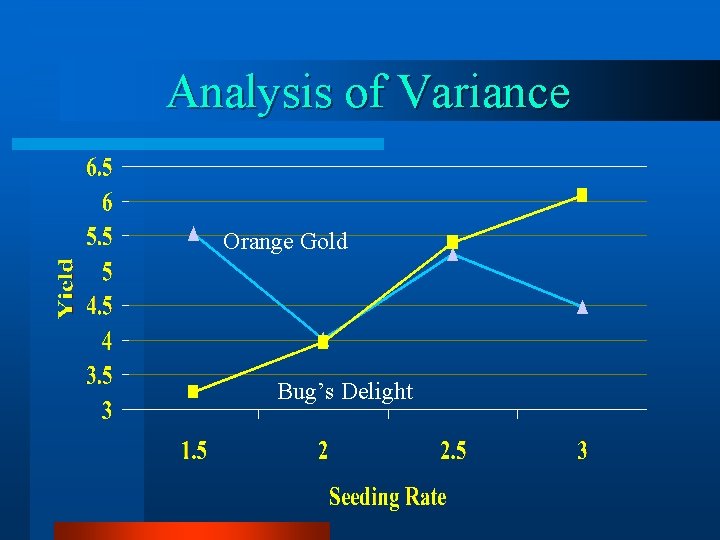
Analysis of Variance Orange Gold Bug’s Delight

End of Analyses of Variance Section