Multiphase Chemical Reactor Engineering Quak Foo Lee Ph



















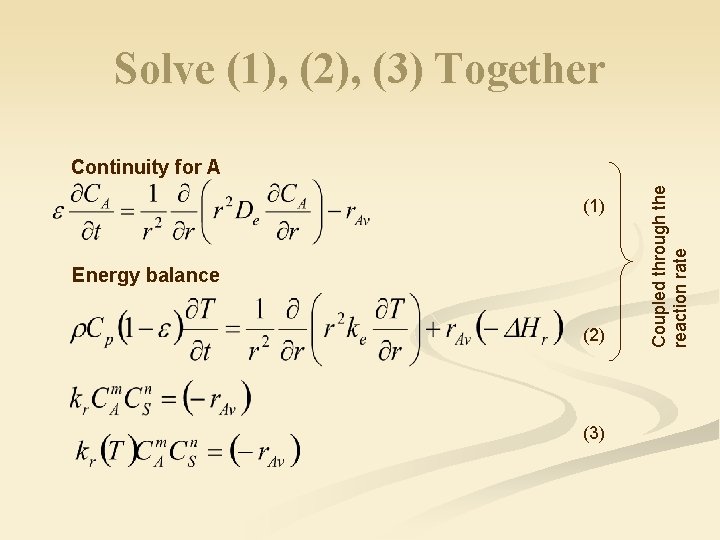










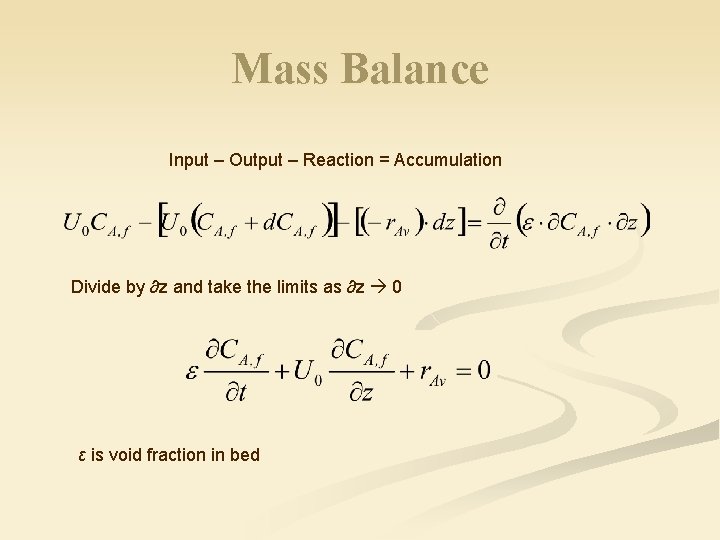














- Slides: 57

Multiphase Chemical Reactor Engineering Quak Foo Lee Ph. D. Candidate Chemical and Biological Engineering The University of British Columbia

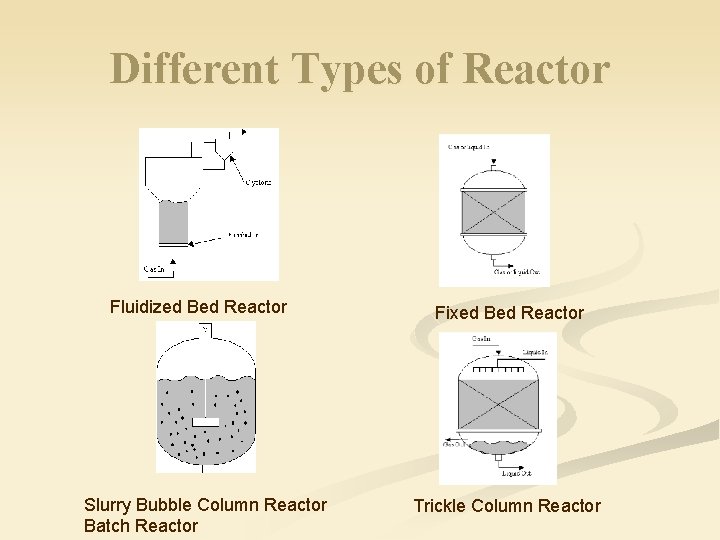
Different Types of Reactor Fluidized Bed Reactor Slurry Bubble Column Reactor Batch Reactor Fixed Bed Reactor Trickle Column Reactor

Fixed Bed Rector Fixed Bed Reactor that converts sulfur in diesel fuel to H 2 S

Fluidized Bed Reactor using H 2 SO 4 as a catalyst to bond butanes and iso-butanes to make high octane gas

Batch Reactor Stirring Apparatus

Straight Through Transport Reactor Riser Settling Hopper Standpipe The reactor is 3. 5 m in diameter and 38 m tall. Sasol/Sastech PT Limited

Slurry Phase Distillate Reactor

Packed Bed Reactor

CSTR Hand holes for charging reactor Connection for heating or cooling jacket Agitator

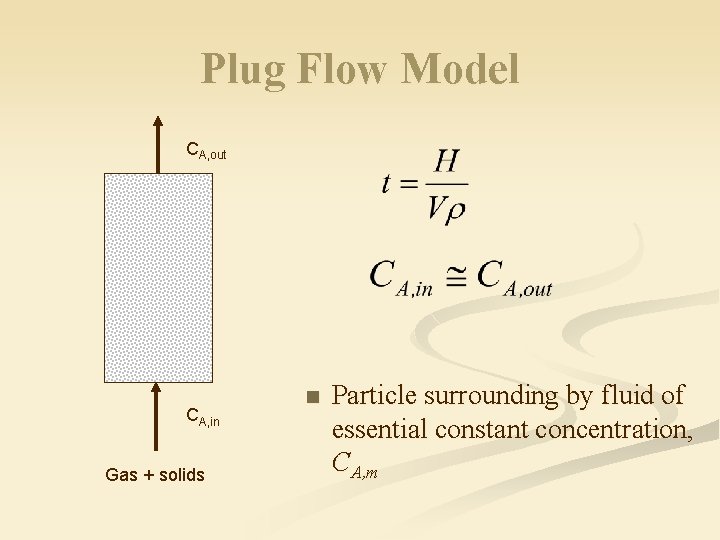
Plug Flow Model CA, out CA, in Gas + solids n Particle surrounding by fluid of essential constant concentration, CA, m

Batch Mix Flow: Charge Reactor n Residence time distribution n Particle stays in the reactor for certain length of time

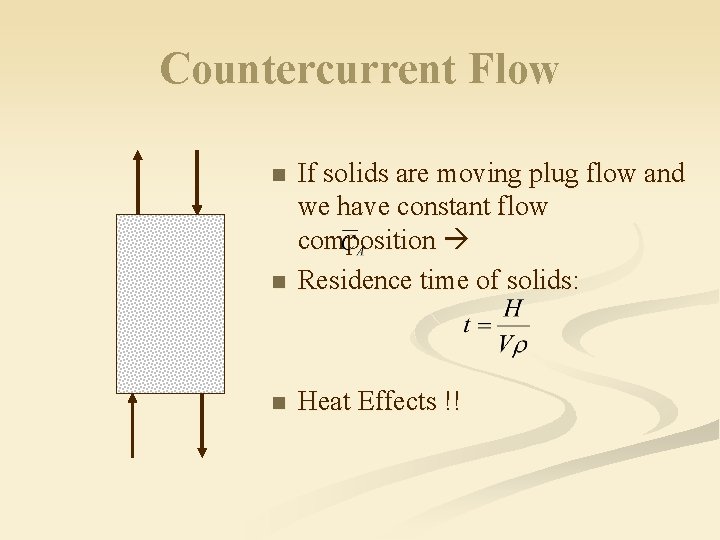
Countercurrent Flow n If solids are moving plug flow and we have constant flow composition Residence time of solids: n Heat Effects !! n

Heat Effects on Reactions of Single Particles n n Normally (developed) dealing with exothermic and endothermic reaction. If reaction occurs at a rate such that the heat absorbed (endothermic) or generated (for exothermic) can’t be transferred rapidly enough, then non-isothermal effects become important: The particle T ≠ the fluid T For exothermic reaction, Tp will increase and the rate of reaction will increase above that expected for the isothermal case. Two conditions: n i) Film ∆T (external ∆T) Tf (bulk fluid) ≠ Tp (particle) n ii) Intraparticle ∆T (internal ∆T) Tr=Rp ≠ Tr=∞

Non-Reacting 1. Small particles highly conductive particles 2. Small particles volumetric reaction

1) Small Particles: Highly Conductive Particles n Tp Fluid at Tf n Particle initially at uniform T = Tp At t = 0, we drop it into our furnace

Energy Balance Heat in by convection and radiation = change in enthalpy of particle Where, Area of sphere = 4πR 2 Hcv = convection coefficient σ = Stefan-Boltzman constant Єm = emissivity of the particle (wall has Є = 1)

Energy Balance Can solve this equation to get Tp =f(t)

Find hcv n n Have film: ∆H Tf ≠ Tp Use mass transfer analogy to get hcv

2. Small Particles: Volumetric Reaction Heat generated by reaction = Heat transferred to surrounding Steady State: n Volume of particle Rate of reaction Small such that no internal gradients Exothermic Rxn: -∆Hr = (+) -r. Av = (+)

3. Large Particles: Possible Internal Particle Gradients n n We have to solve the conduction equation Non reacting particle: the conduction equation for sphere: Ke = effective thermoconductivity within the particle ∂T/∂r = 0 at steady state Heat conducted into particle at r =Rp Heat transferred into particle Note: accommodate radiation in the definition of h if that is the case

Boundary Conditions Symmetry condition Initial condition Internal gradient External gradient

Reacting Systems n General equation for volumetric reactions (Reaction in porous particles) n Recall continuity equation: continuity for A
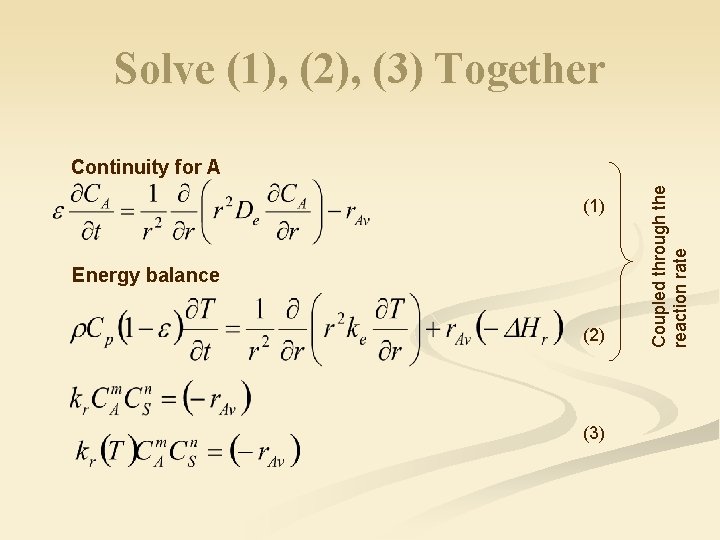
Solve (1), (2), (3) Together (1) Energy balance (2) (3) Coupled through the reaction rate Continuity for A

In Steady State n Showed that for steady conditions: Integrate at r = 0, r = R For sphere

Some Notes n If we know CA, s (surface concentration) and CA, r=0 (CA within pellet at r = 0), we can calculate temperature gradient, previous equation tell us either we need or don’t need to worry about T gradient within particle. n Where isothermal (approach) approximation can be used and where internal T gradients must be considered. n Volumetric reaction for porous particles, heat is generated in a volume.

Shrinking Core: Non-Isothermal Tc n Ts Heat generated at reaction front, not throughout the volume rc r n In Steady State, n Solve R Tf

T Conditions

Boundary Condition 1: r = rc Heat is generated = Heat conducted out through product layer Area

Boundary Condition 2: r = R Heat arriving by conduction from within particle = Can be obtained from B. C. 1 Heat removed for convection Bi-1

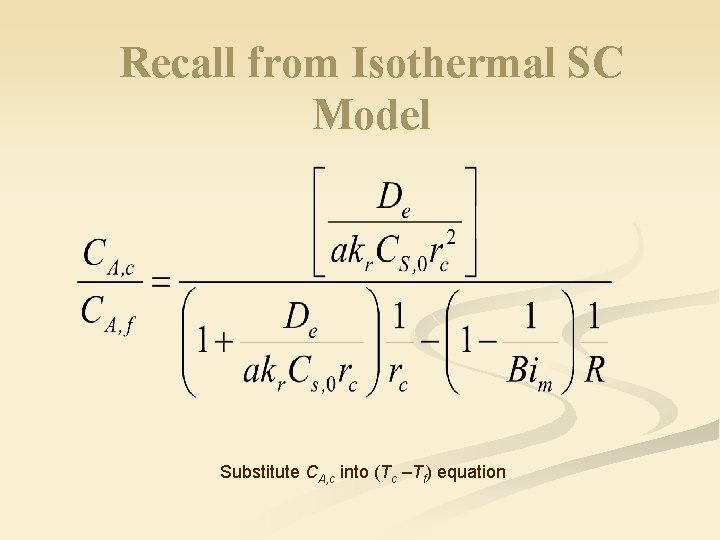
Solution n Combine equations and eliminate TS to get Tc-Tf

Recall from Isothermal SC Model Substitute CA, c into (Tc –Tf) equation

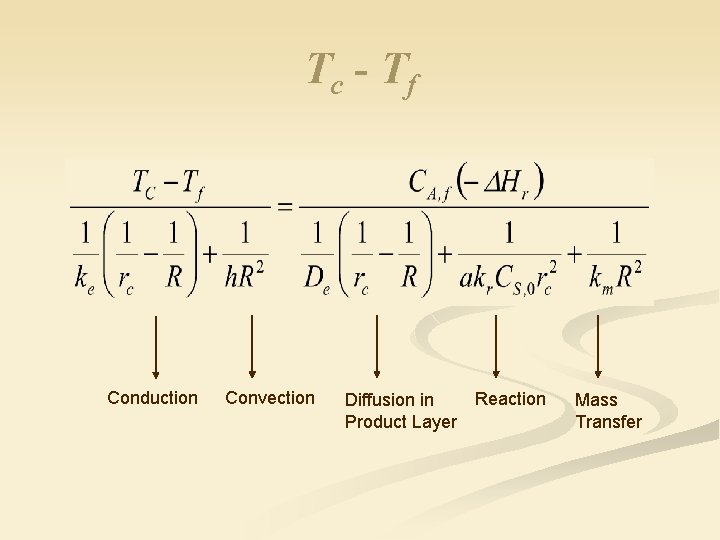
Tc - Tf Conduction Convection Diffusion in Product Layer Reaction Mass Transfer


Can Heat Transfer Control the Rate in Endo- and Exothermal Rxn? n Consider CA, c ≈ CA, f; initially rapid reaction a) Endothermic with poor heat transfer, heat will be consumed in reaction, and if can’t transfer heat in, TC will drop reaction rate ↓ markedly and rate of reaction become the slow step occurring at a rate dictated by the flow of heat. b) Exothermic initial rapid reaction and with poor Q, TC will increased, then rate of reaction ↑ and eventually reach point where gaseous reactant can’t be transferred fast enough (external mass transfer or diffusion). Hence rate is limited.

Fixed Bed Reactor

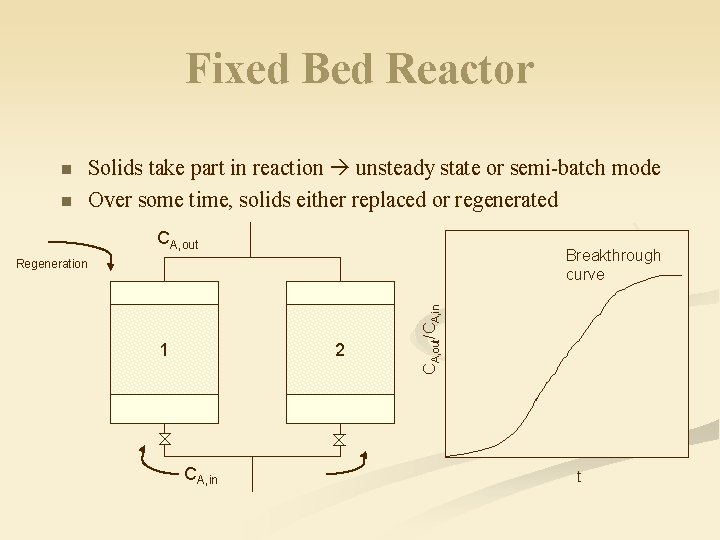
Fixed Bed Reactor n n Solids take part in reaction unsteady state or semi-batch mode Over some time, solids either replaced or regenerated CA, out Breakthrough curve 1 2 CA, in CA, out/CA, in Regeneration t

Isothermal Reaction: Plug Flow Reactor n Plug flow of fluid – no radial gradients, and no axial dispersion n Constant density with position n Superficial velocity remains constant

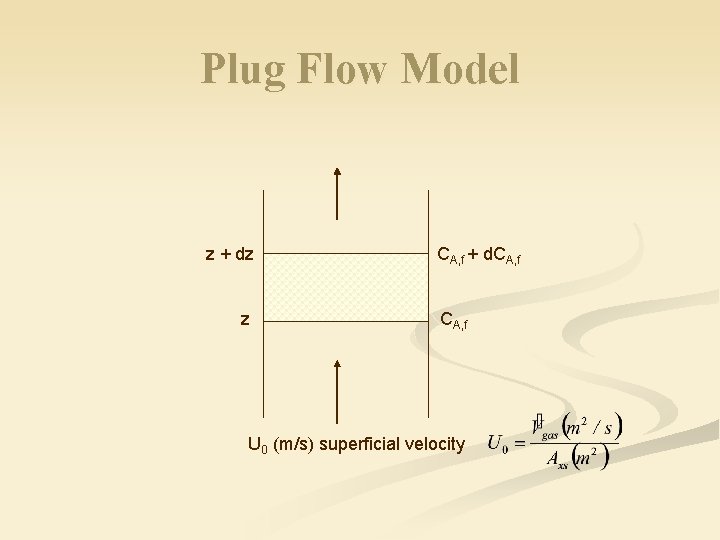
Plug Flow Model z + dz z CA, f + d. CA, f U 0 (m/s) superficial velocity
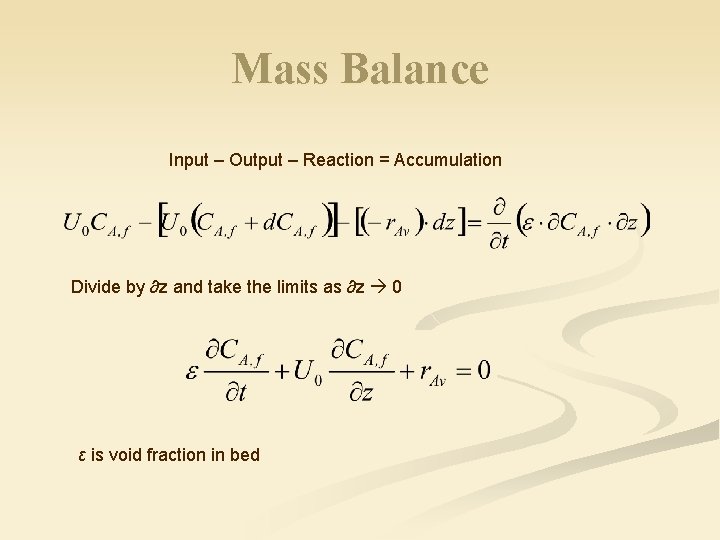
Mass Balance Input – Output – Reaction = Accumulation Divide by ∂z and take the limits as ∂z 0 ε is void fraction in bed

For first order reaction, fluid only: For steady state: Therefore, Void fraction Volume of reactor

Conversion as a function of Height Integrating with CA, f = CA, f, in at z = 0 Note 1: Same equation as for catalytic reactor with 1 st order reaction Note 2: Can be used in pseudo-homogeneous reaction

Balance on Solid n n n a. A (fluid) + S (solid) Products Input – Output – Reaction = Accumulation Over increment of dz: input = 0, output =0 Volume fraction of solid = m 3 of solid m 3 of reactor volume mol m 3 of solid · s

Balance on Solid

Solve These Equations Su bs titu te r. A v = 0 (In quasi steady state, we ignore the accumulation of A in gas)

a) b) c) d) e) Shrinking Core Model Uniform reaction in porous particle, zero order in fluid Uniform reaction, 1 st order in fluid and in solid Park et al. , “An Unsteady State Analysis of Packed Bed Reactors for Gas-Solid Reactions”, J. Chem. Eng. Of Japan, 17(3): 269 -274 (1984) Evans et al. , “Application of a Porous Pellet Model to Fixed, Moving and Fluid Bed Gas-Solid Reactors”, Ind. Eng. Chem. Proc. Des. 13(2): 146 -155 (1974)

a) In Shrinking Core Model Recall that Solid Phase Liquid Phase For SCM Solve CA, f = f(z) rc = f(z, t)

Conversion vs Time t=0 z t>0

Overall Conversion of Solid

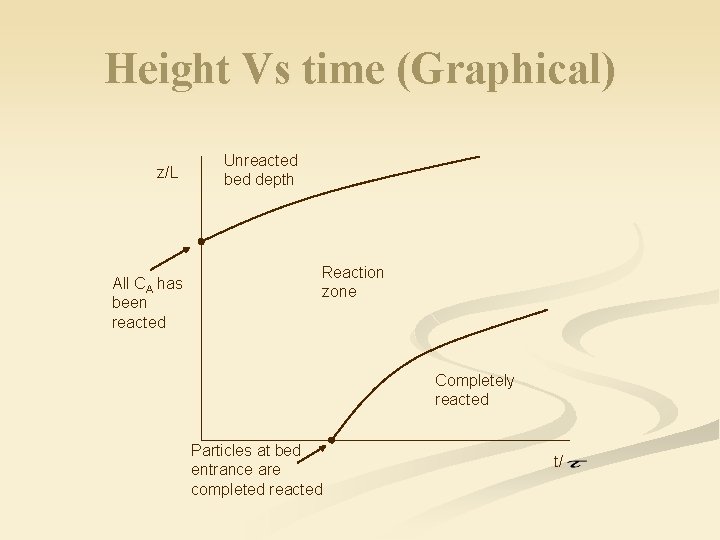
Height Vs time (Graphical) z/L All CA has been reacted Unreacted bed depth Reaction zone Completely reacted Particles at bed entrance are completed reacted t/

b) Uniform Reaction in Porous Particle and Zero Order in Fluid where

c) Uniform Reaction and 1 st order in Fluid and in solid

Non-Isothermal Packed Bed Reactor For mass continuity did balance on fluid and on solid n For energy balance, we do balance on each phase n

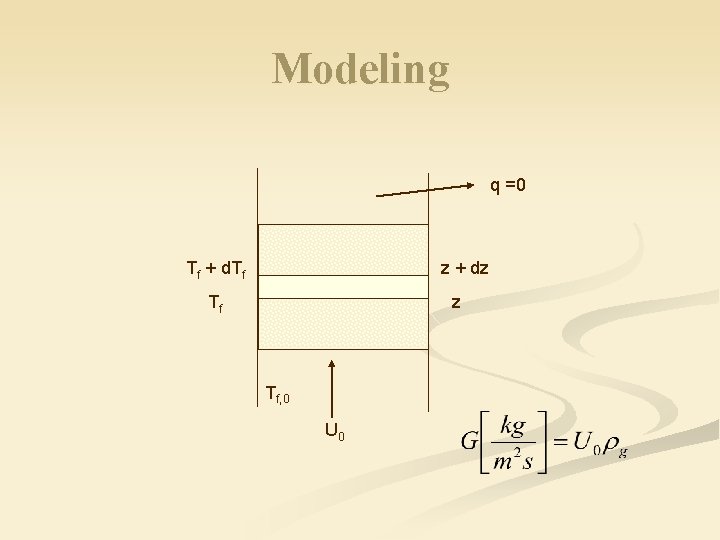
Non-Isothermal Packed Bed Reactor n Assumptions: 1) Adiabatic reaction – no heat lost through shell to surroundings (no radial temperature gradients) q =0 2) Biλ is small – uniform T within particle (an exothermic reaction Tp > Tg) 3) Plug flow of gas and use Tref =0 for enthalpy calculations 4) Assume an average density can be used (ρg = constant)

Modeling q =0 Tf + d. Tf z + dz Tf, 0 U 0

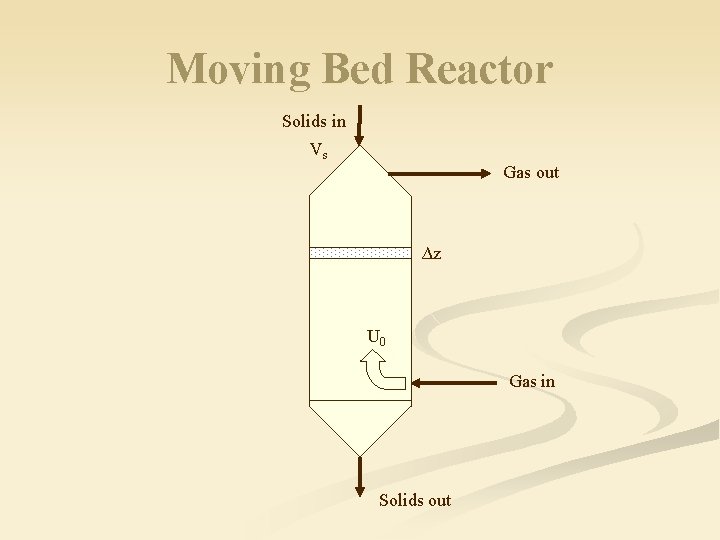
Moving Bed Reactor Solids in Vs Gas out ∆z U 0 Gas in Solids out

Moving Bed Reactor (MBR) n n n Steady state reactor where solids moving at near their packed bed voidage Counter or co-current operation Solid usually move downward (vertical shaft reactor or furnace) Voidage is near that of a packed bed n Slightly above random loose-packed voidage Solids move mainly in a plug floe, but region near wall have a velocity distribution

Advantages of MBR n n n True counter-current flow Uniform residence time (essentially plug flow) Reasonable ∆P Throughput variable Generally larger particle dp > 2 -3 mm Difficulties coping with wide size distribution of particles (fines tend to block up the void spaces)