Multilinear NC 1 Multilinear NC 2 Ran Raz

Multilinear NC 1 Multilinear NC 2 Ran Raz Weizmann Institute

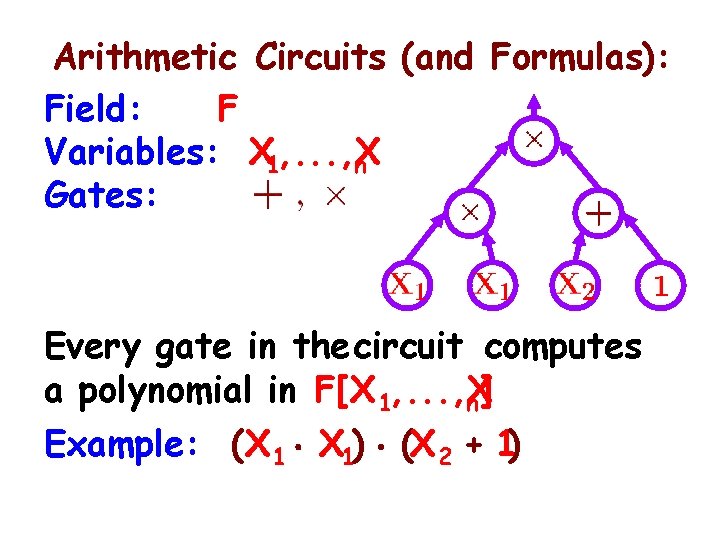
Arithmetic Circuits (and Formulas): Field: F Variables: X 1, . . . , X n Gates: Every gate in the circuit computes a polynomial in F[X 1, . . . , X n] Example: (X 1 ¢ X 1) ¢ (X 2 + 1)

Classes of Arithmetic Circuits: NC 1: Size: poly(n) Degree: poly(n) Depth: O(log n) (poly-size formulas) NC 2: Size: poly(n) Degree: poly(n) Depth: O(log 2 n) P : Size: poly(n) Degree: poly(n)

Valiant Skyum Berkowitz Rackoff: Arithmetic NC 2 = Arithmetic P [H]: poly-size arithmetic circuit ! quasipoly-size arithmetic formula Outstanding open problem: Arithmetic NC 1 Arithmetic NC 2 Are arithmetic formulas weaker than arithmetic circuits ?

Multilinear Circuits: [NW]: Every gate in the circuit computes a multilinear polynomial Example: (X 1 ¢ X 2) + (X 2 ¢ X 3) (no high powers of variables)

Motivation: 1) For many functions, non-multilinear circuits are very counter-intuitive 2) For many functions, most (or all) known circuits are multilinear 3) Multilinear polynomials: interesting subclass of polynomials 4) Multilinear circuits: strong subclass of circuits (contains other classes) 5) Relations to quantum circuits [Aaronson]

Previous Work : [NW 95]: Lower bounds for a subclass of constant depth multilinear circuits [Nis, NW, RS]: Lower bounds for other subclasses of multilinear circuits [R 04]: Multilinear formulas for Determinant and Permanent are of size [Aar 04]: Lower bounds for multilinear formulas for other functions

Our Result: Explicit f(X 1, . . . , X n), with coeff. in {0, 1}, s. t. , over any field: 1) 9 poly-size NC 2 multilinear circuit for f 2) Any multilinear formula for f is of size multilinear NC 1 multilinear NC 2

Partial Derivatives Matrix [Nis]: f = a multilinear polynomial over {y 1, . . . , y m} [ {z 1, . . . , z m} P = set of multilinear monomials in m {y 1, . . . , y }. P| | = 2 m Q = set of multilinear monomials in m {z 1, . . . , z }. Q| | = 2 m

Partial Derivatives Matrix [Nis]: f = a multilinear polynomial over {y 1, . . . , y m} [ {z 1, . . . , z m} P = set of multilinear monomials in {y 1, . . . , y P| | = 2 m m}. Q = set of multilinear monomials in m {z 1, . . . , z }. Q| | = 2 m M = Mf = 2 m dimensional matrix: For every p 2 P, q 2 Q, Mf(p, q) = coefficient of pq in f

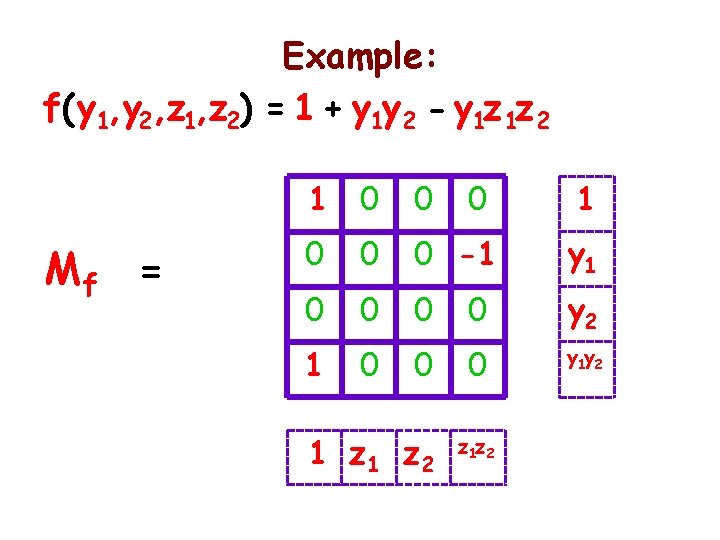
Example: f(y 1, y 2, z 1, z 2) = 1 + y 1 y 2 - y 1 z 1 z 2 Mf = 1 0 0 0 -1 y 1 0 0 y 2 1 0 0 0 y 1 y 2 1 z 2 0 z 1 z 2 1

Partial Derivatives Method [N, NW] [Nis]: If f is computed by a noncommutative formula of size s then Rank(Mf) = poly(s) [NW, RS]: The same for other classes of formulas Is the same true for multilinear formulas ?

Counter Example: Mf is a permutation matrix Rank(Mf) = 2 m

We Prove: Partition (at random) {X 1, . . . , X 2 m } ! {y 1, . . . , y z m} m} [ {z 1, . . . , If f has poly-size multilinear formula, then (w. h. p. ): If for every partition Rank(Mf)=2 m then any multilinear formula forf is of super-poly-size ( )

High-Rank Polynomials: Define: f(X 1, . . , X 2 m ) is High-Rank if for every partition Rank(Mf)=2 m f is High-Rank ! any multilinear formula for f is of super-poly-size

Our Result: Step 1 Explicit f(X 1, . . , X 2 m ) over C, s. t. : 1) 9 poly-size NC 2 multilinear circuit for f 2) f is High-Rank (coefficients different than 0, 1) (We use algebraicly independent constants from C)

Our Result: Step 2 Explicit f(X 1, . . , X 2 m , X’ 1, . . , X’ r), with coeff. in {0, 1}, and r=poly(m), s. t. (over any field) 1) 9 poly-size NC 2 multilinear circuit for f 2) a 1, . . , a r algeb. independent ! f(X 1, . . , X 2 m , a 1, . . , a r) is High-Rank

Our Result: Step 3 If F is a finite field take. F ½ G of infinite transcendental dimension (G contains an infinite number of algeb. independent elements) Step 2 ! lower bound over G ! lower bound over F

The End