MultiLimb Robots on Irregular Terrain NASAJPLs LEMUR Robot

Multi-Limb Robots on Irregular Terrain

NASA/JPL’s LEMUR Robot

Only friction and internal degrees of freedom are used to achieve equilibrium F r e e C l i m b i n g

Other Climbing Robots Cutkosky, Stanford, 2004 NINJA II Hirose et al, 1991 Yim, PARC, 2002

Free climbing is a problem -solving activity § Each step is unique § Where to make contact? § Which body posture to take? § Which forces to exert? § Decisions at one step may affect the ability to perform future steps

ATHLETE (NASA/JPL)

HRP-2 (AIST, Japan)

Motion-Before-Stances Approach Suitable when the terrain is mostly even and horizontal Stances-Before-Motion Approach
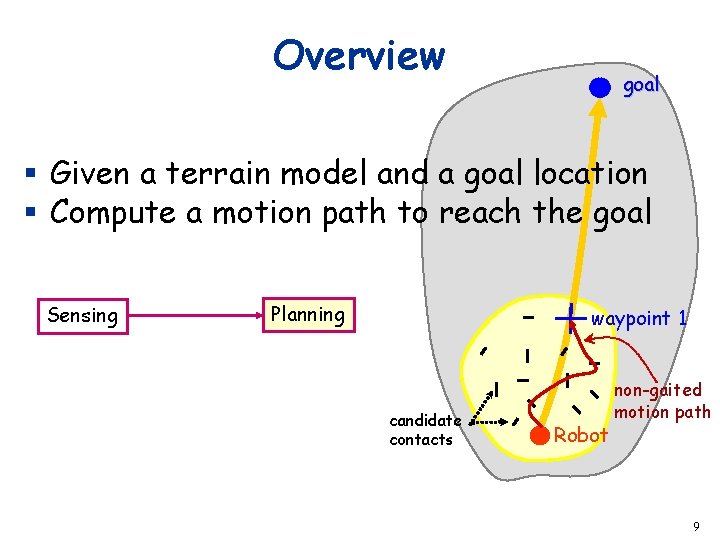
Overview goal § Given a terrain model and a goal location § Compute a motion path to reach the goal Sensing Planning waypoint 1 candidate contacts Robot non-gaited motion path 9
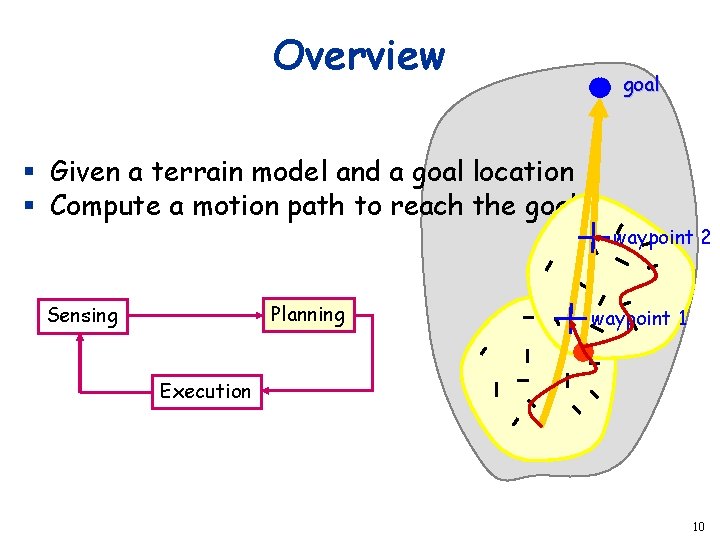
Overview § Given a terrain model and a goal location § Compute a motion path to reach the goal Planning Sensing goal waypoint 2 waypoint 1 Execution 10

Key Concept: Stance § Set of fixed robotenvironment contacts § Fs: space of feasible robot configurations at stance s 3 -stance of LEMUR 1. 2. 3. 4. Contacts Quasi-static equilibrium No (self-)collision Torques within bounds Feasible motion at 4 -stance

Inverse Kinematics Problem
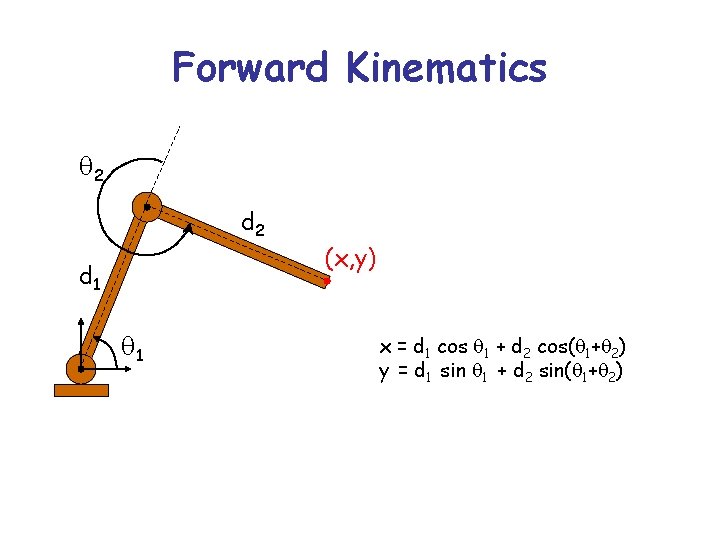
Forward Kinematics q 2 d 1 q 1 (x, y) x = d 1 cos q 1 + d 2 cos(q 1+q 2) y = d 1 sin q 1 + d 2 sin(q 1+q 2)
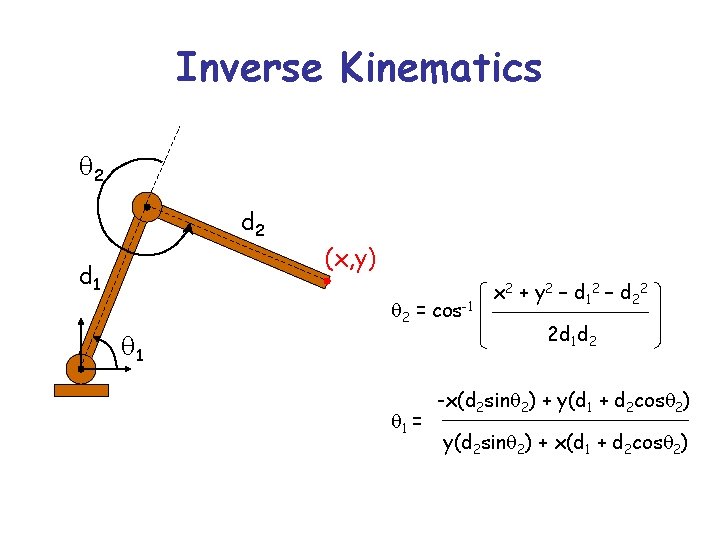
Inverse Kinematics q 2 d 1 (x, y) q 2 = cos-1 q 1 = x 2 + y 2 – d 12 – d 22 2 d 1 d 2 -x(d 2 sinq 2) + y(d 1 + d 2 cosq 2) y(d 2 sinq 2) + x(d 1 + d 2 cosq 2)
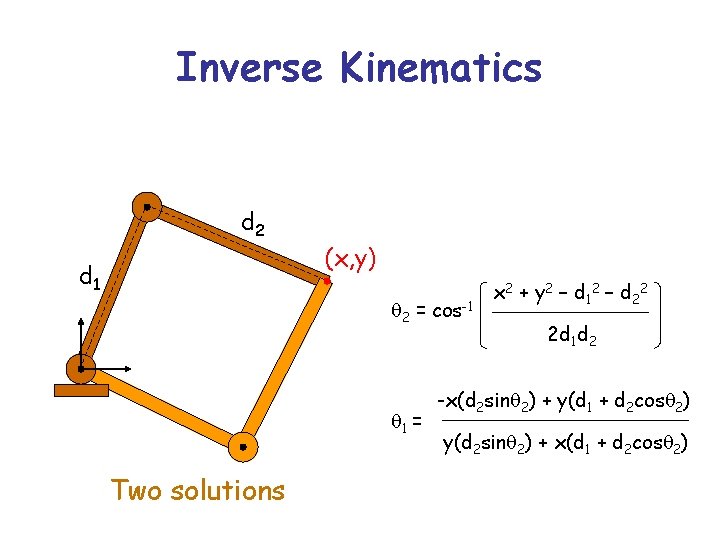
Inverse Kinematics d 2 d 1 (x, y) q 2 = cos-1 q 1 = Two solutions x 2 + y 2 – d 12 – d 22 2 d 1 d 2 -x(d 2 sinq 2) + y(d 1 + d 2 cosq 2) y(d 2 sinq 2) + x(d 1 + d 2 cosq 2)

More Complicated Example q 2 d 2 (x, y) d 3 q 3 d 1 q 1 § Redundant linkage § Infinite number of solutions § Self-motion space
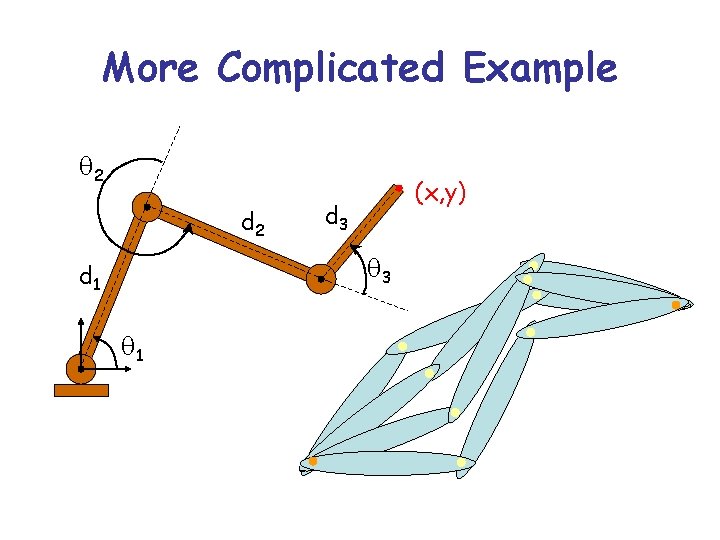
More Complicated Example q 2 d 2 (x, y) d 3 q 3 d 1 q 1
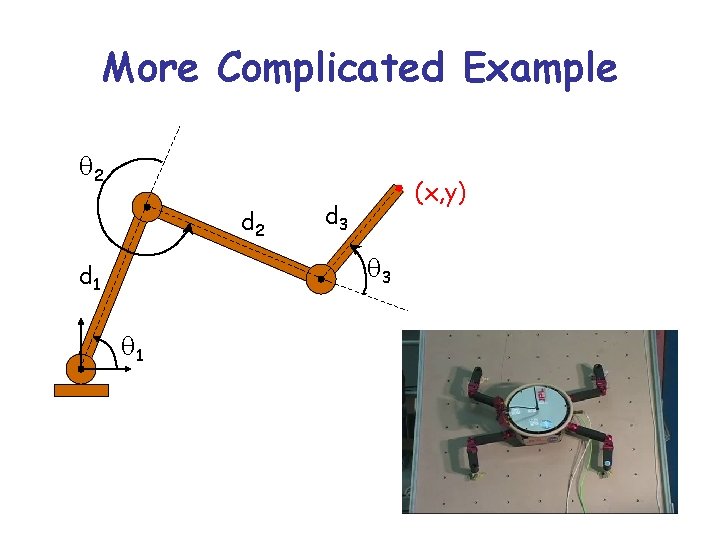
More Complicated Example q 2 d 2 (x, y) d 3 q 3 d 1 q 1

Challenge § High-dimensional configuration space C (11 LEMUR, 42 for ATHLETE, 36 for HRP-2, 16 for Stanford robot) § Many possible contacts, hence many stances C Fs
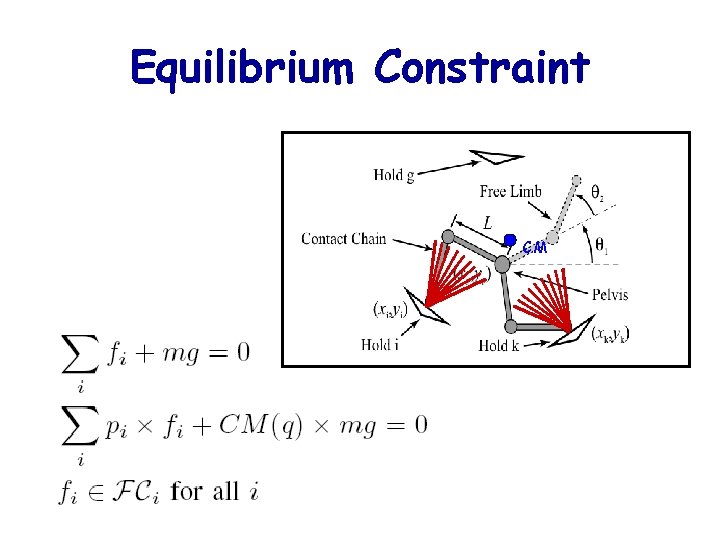
Equilibrium Constraint CM

backstep highstep lieback
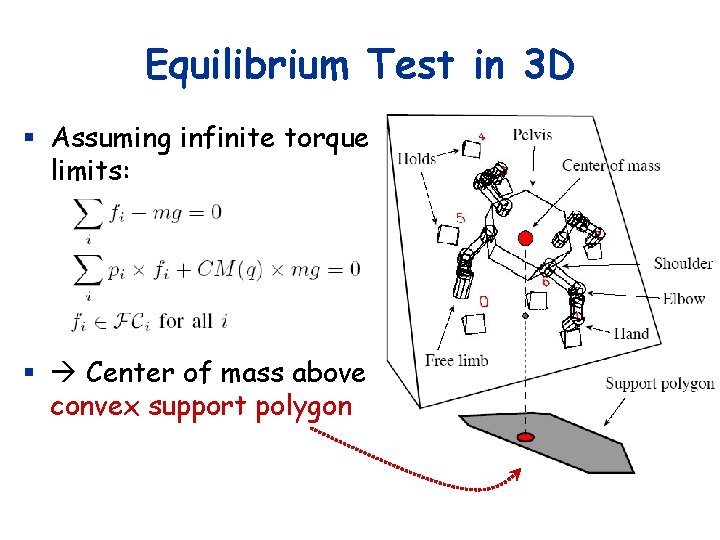
Equilibrium Test in 3 D § Assuming infinite torque limits: § Center of mass above convex support polygon

Equilibrium Test § Assuming infinite torque limits: § Center of mass above convex support polygon CM

Equilibrium Test § Assuming infinite torque limits: § Center of mass above convex support polygon

Transition Configuration Zero force
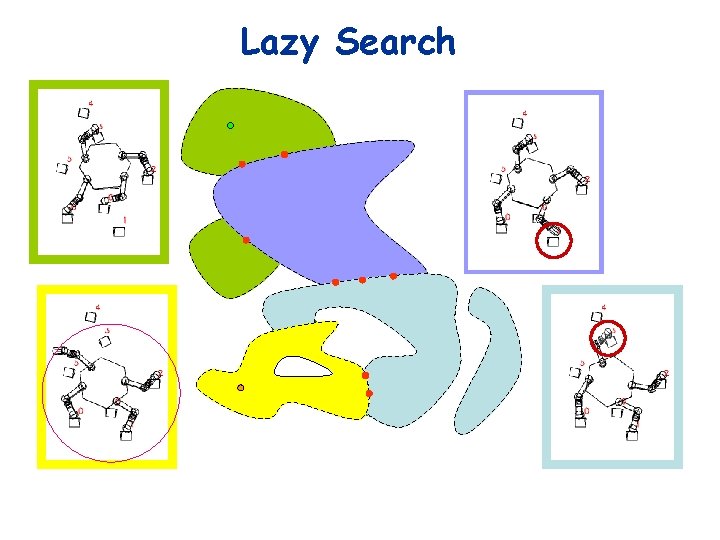
Lazy Search
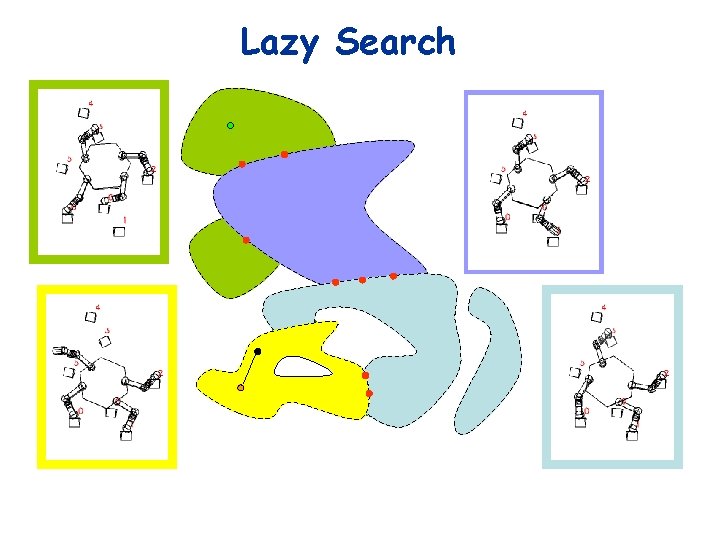
Lazy Search
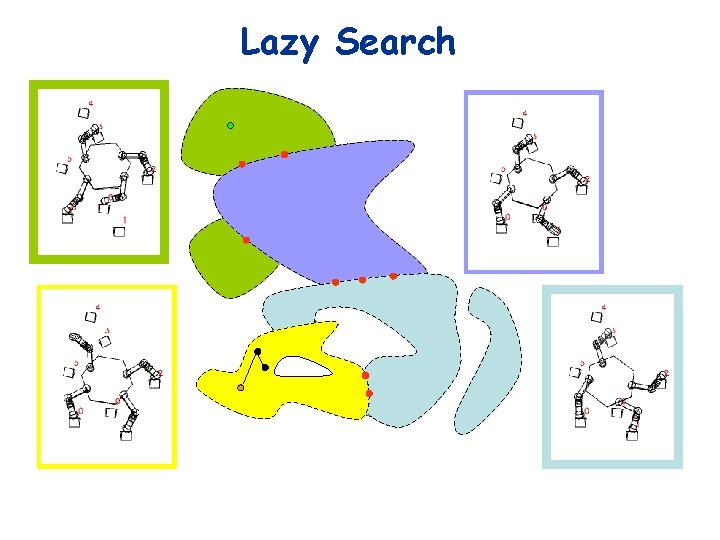
Lazy Search
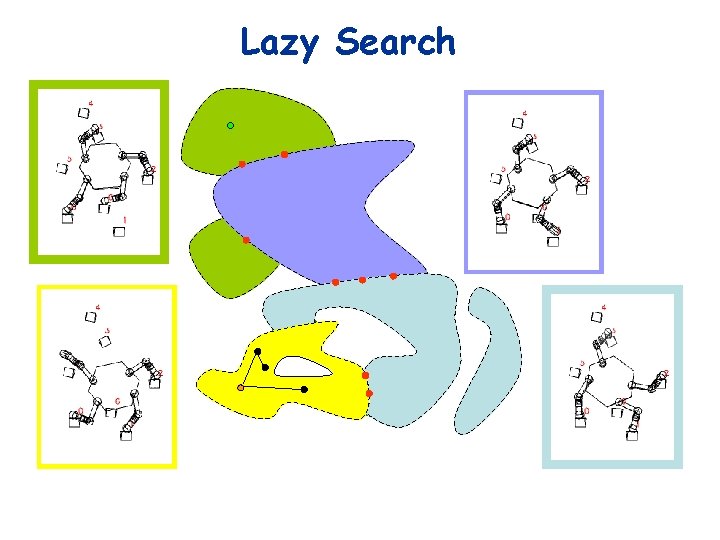
Lazy Search
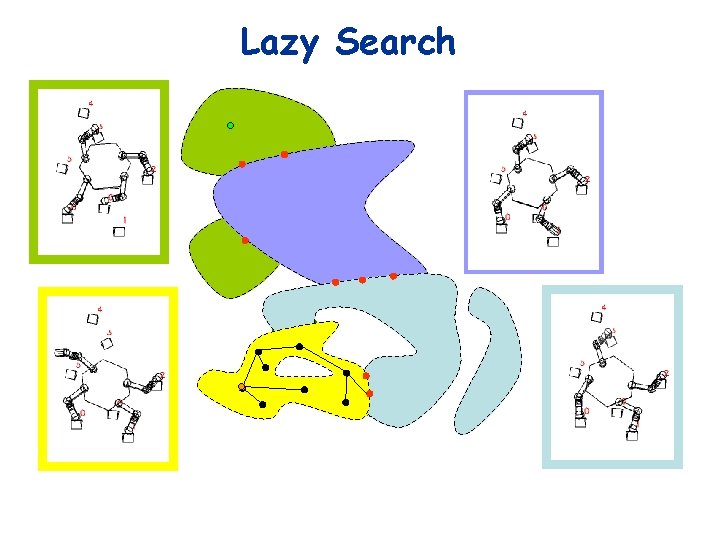
Lazy Search
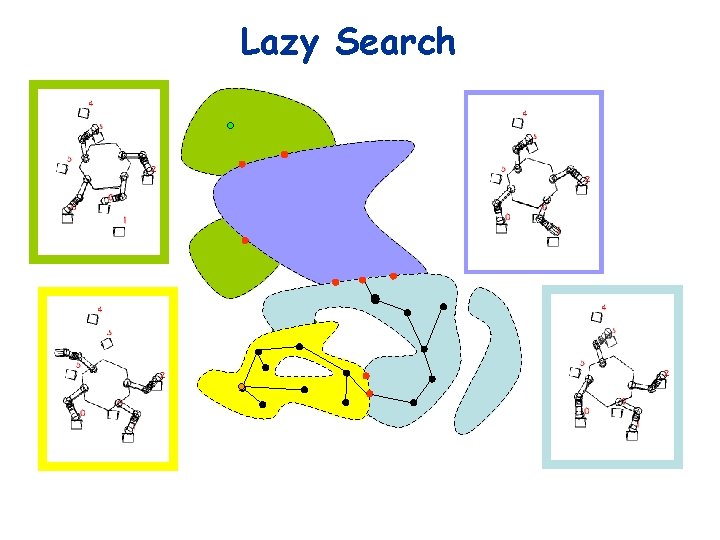
Lazy Search
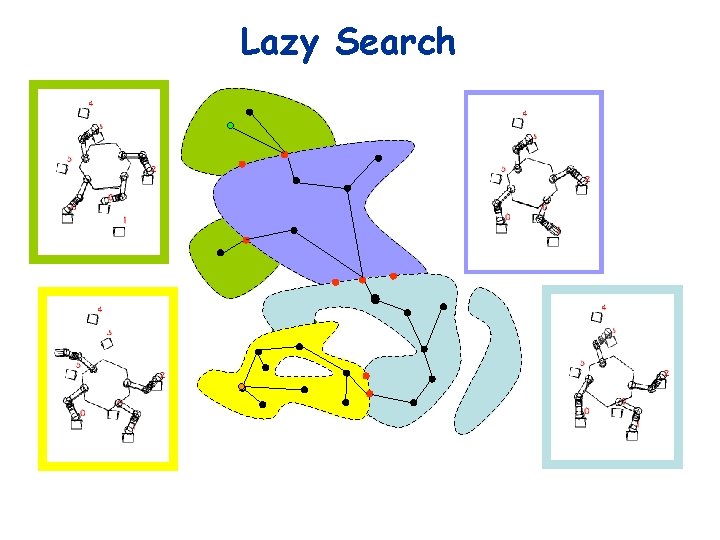
Lazy Search
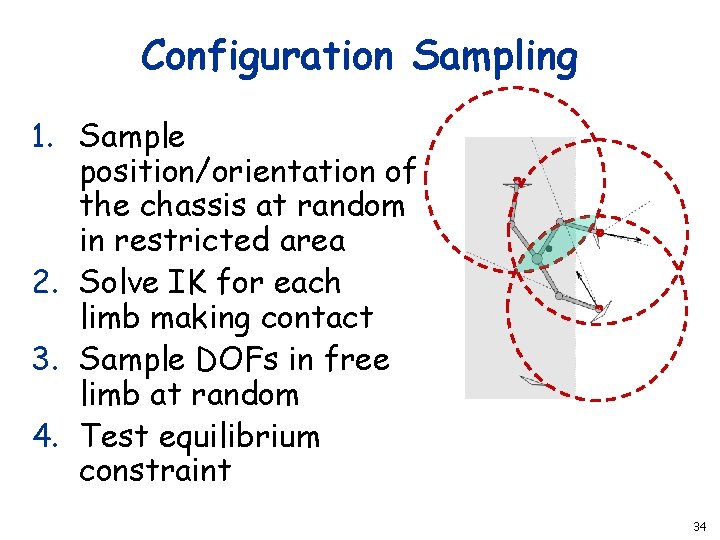
Configuration Sampling 1. Sample position/orientation of the chassis at random in restricted area 2. Solve IK for each limb making contact 3. Sample DOFs in free limb at random 4. Test equilibrium constraint 34

35

Need for Sensor Feedback
- Slides: 36