Multilevel Modelling of PLASC data Harvey Goldstein University

Multilevel Modelling of PLASC data Harvey Goldstein University of Bristol

Data structure • Students nested within schools • Students changing schools over time • Students moving between stages (e. g. Junior – Secondary) • Students nested within neighbourhoods • Students moving between neighbourhoods • Statistical modelling requires use of crossclassifications and multiple membership models

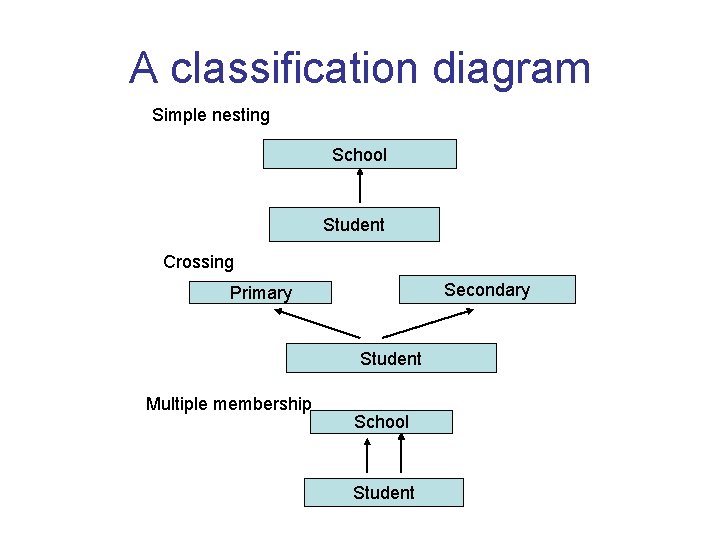
A classification diagram Simple nesting School Student Crossing Secondary Primary Student Multiple membership School Student

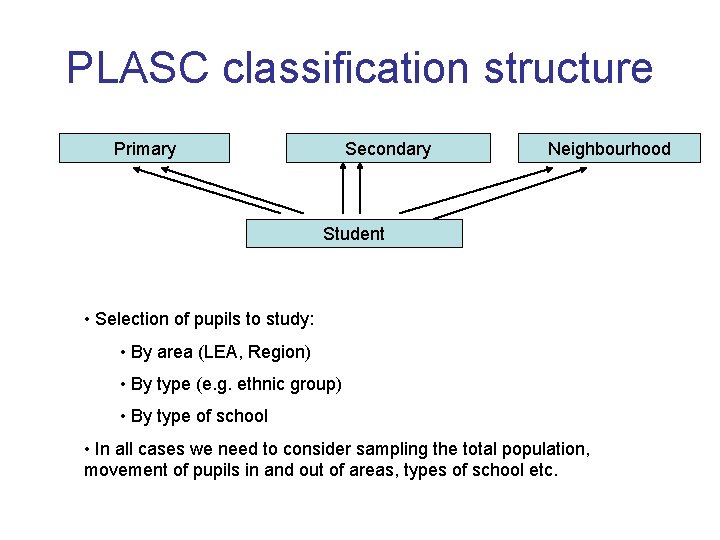
PLASC classification structure Primary Secondary Neighbourhood Student • Selection of pupils to study: • By area (LEA, Region) • By type (e. g. ethnic group) • By type of school • In all cases we need to consider sampling the total population, movement of pupils in and out of areas, types of school etc.

Case study: all students in an LEA Issues: 1. How to deal with movement in and out (mobility) 2. How to measure time in each school 3. How to deal with ‘special’ schools 4. How to measure and use composition of school 5. How well does a ‘simple’ analysis approximate a full ‘structural’ model ?

Data and Mobility (turbulence) • Study of Secondary years 7 – 9. KS 3 scores as outcome; KS 2 as predictor; FSM, gender, ethnic group. • Mobility is movement between secondary schools (and possibly neighbourhoods) • We compare MM model with standard model using only KS 3 school • We also study cross classification of KS 2 school by secondary school(s).

Time in each school • Multiple membership requires us to weight school level contribution in proportion to time in each school. • PLASC only allows us to approximate these. • We know school each January and at KS 2 and at KS 3 • Units of measurement are 0. 4, 0. 6, 1. 0 year.

‘Special’ schools • Some schools are very small and may take just SEN pupils for example. • We can deal with them as a separate category – we have in fact excluded them since they are few in number • Including them greatly increases the between school variation

Compositional effects 1. 2. 3. 4. average KS 2 scores of KS 3 cohort proportion FSM eligible for KS 3 cohort Proportion of minority ethnic groups Average KS 2 score for those remaining in KS 3 school years 7 – 9; average for those not 5. Proportion of girls averaged over years 7 – 9 that student encounters in schools attended

Some results for Maths Intercept and KS 2 only – Hampshire years 7 -9 Simple Models with no MM using KS 3 school + various predictors – no cohorts < 30 Note: correlation between residuals using Yr 7 rather than Yr 9 as ID is 0. 90

For contrast -intercept only

Multiple membership model Also includes non-Hampshire schools years 7 & 8

Exclusions • We have 13 pupils who are in secondary schools outside Hampshire in yr 7 and year 8 where these schools do not appear elsewhere in data set. These have been excluded from the analysis as has 1 student who is not in Hampshire school in year 9. • We have also excluded pupils (200 or so) who are in 146 schools that do not appear to have Hamshire secondary IDs ( i. e. not beginning with 850). This leaves 170 schools.

MM vs simple hierarchy • Level 2 variance increases by about 11% using MM model. For these data the % students not in same school years 7 -9 is about 5%. • Now look at more complex models • These cross-classify students by Yr 7 school – subscript v is primary, u is secondary

Intcpt + KS 2 score + XC primary No Multiple membership. Adding mean KS 2 score for class student was in at year 7 (s_ks 2 mean_po 2), FSM eligibility at year 9 and year 7 (fsm_po 4_1, fsm_po 2_1) and gender (boy)

Now adding MM at secondary

Inferences • Note primary school variance about twice that for secondary: primary schools are smaller and more homogeneous. Similar results in other studies • Now MM model increase in level 2 variance is about 5%. • Note significant effects of FSM status at both ages – 5% change status.

FSM YR 9 x YR 7 • 0 1 TOTALS • 0 11843 307 12150 • 1 335 571 906 • TOTALS 12178 878 13056

Conclusions • Ignoring multiple membership where % mobility about 5% implies underestimation of level 2 variance up to ~ 11% • Adding primary school identification reduces level 2 secondary variance by ~ 15% but gives primary school variance up to twice secondary school variance. • The estimated school effects will also change.