Multilevel Modeling Multilevel Question Turns out the Simple

Multilevel Modeling

Multilevel Question • • Turns out the Simple Random Sampling is very expensive Travel to Moscow, Idaho to give survey to a single student. The subsets are conventionally called primary sampling units or psu's. In a two-stage sample, rst a sample is drawn from the primary sampling units (the rst-stage sample), and within each psu included in the rst-stage sample, a sample of population elements is drawn (the second-stage sample). This can be extended to situations with more than two levels, e. g. , individuals within households within municipalities, and then is called a multistage sample.

These are examples of two-level data structures, but extensions to multiple levels n are possible: 10 cities ->In each city: 5 schools ->In each school: 2 classes ->In each class: 5 students ->Each student given the test twice n

What is Multilevel or Hierarchical Linear Modeling? Nested Data Structures

Individuals Undivided Unit of Analysis = Individuals

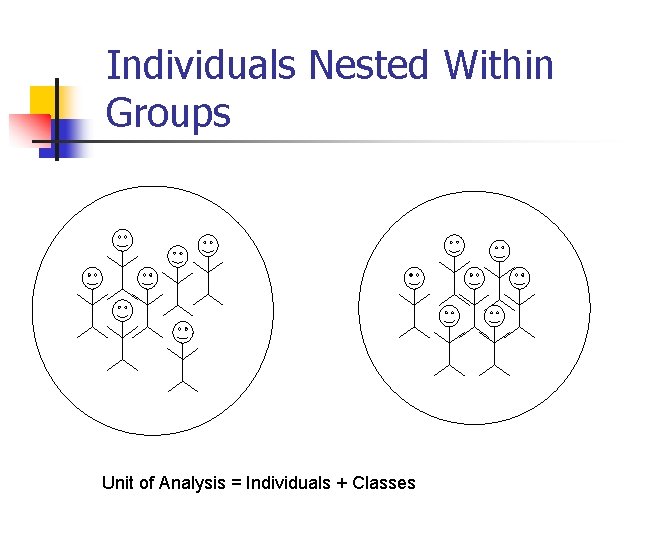
Individuals Nested Within Groups Unit of Analysis = Individuals + Classes

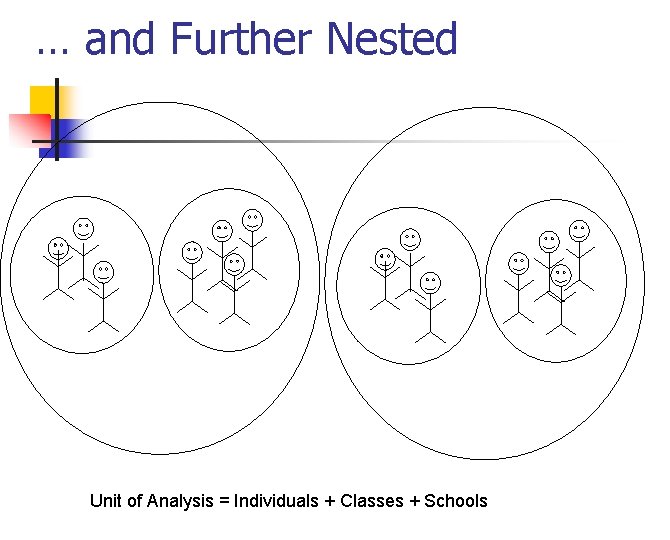
… and Further Nested Unit of Analysis = Individuals + Classes + Schools

Examples of Multilevel Data Structures n n n Neighborhoods are nested within communities Families are nested within neighborhoods Children are nested within families

Examples of Multilevel Data Structures n Schools are nested within districts n Classes are nested within schools n Students are nested within classes

Multilevel Data Structures Level 4 District (l) Level 3 School (k) Level 2 Class (j) Level 1 Student (i)

2 nd Type of Nesting n Repeated Measures Nested Within Individuals Focus = Change or Growth

Time Points Nested Within Individuals

Nested Data n n Data nested within a group tend to be more alike than data from individuals selected at random. Nature of group dynamics will tend to exert an effect on individuals.

Nested Data n Intraclass correlation (ICC) provides a measure of the clustering and dependence of the data 0 (very independent) to 1. 0 (very dependent) Details discussed later

Multilevel Modeling Seems New But…. Extension of General Linear Modeling Simple Linear Regression Multiple Linear Regression ANOVA ANCOVA Repeated Measures ANOVA

Why Multilevel Modeling vs. Traditional Approaches? Traditional Approaches – 1 -Level 1. 2. Individual level analysis (ignore group) Group level analysis (aggregate data and ignore individuals)

Problems with Traditional Approaches 1. Individual level analysis (ignore group) Violation of independence of data assumption leading to misestimated standard errors (standard errors are smaller than they should be).

Problems with Traditional Approaches 1. Group level analysis (aggregate data and ignore individuals) Aggregation bias = the meaning of a variable at Level-1 (e. g. , individual level SES) may not be the same as the meaning at Level-2 (e. g. , school level SES)

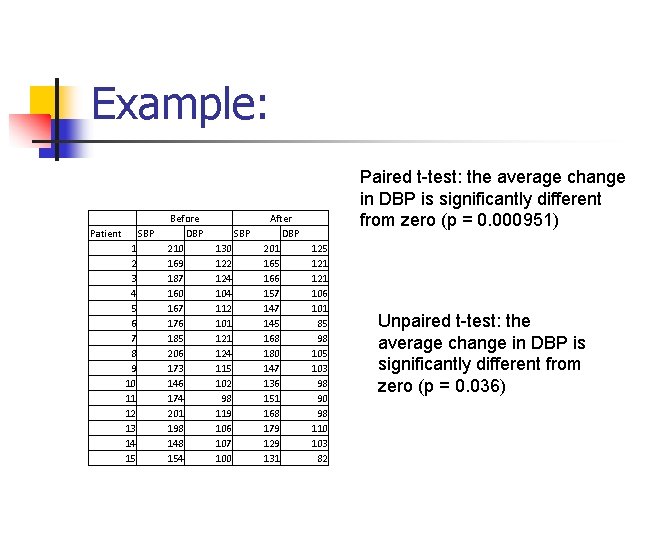
Example: Patient SBP 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Before DBP 210 169 187 160 167 176 185 206 173 146 174 201 198 148 154 SBP 130 122 124 104 112 101 124 115 102 98 119 106 107 100 After DBP 201 165 166 157 145 168 180 147 136 151 168 179 129 131 Paired t-test: the average change in DBP is significantly different from zero (p = 0. 000951) 125 121 106 101 85 98 105 103 98 90 98 110 103 82 Unpaired t-test: the average change in DBP is significantly different from zero (p = 0. 036)

Multilevel Approach n n 2 or more levels can be considered simultaneously Can analyze within- and betweengroup variability

How Many Levels Are Usually Examined? 2 or 3 levels very common 15 students x 10 classes x 10 schools = 1, 500

Types of Outcomes n n n Continuous Scale (Achievement, Attitudes) Binary (pass/fail) Categorical with 3 + categories

Effect for estimation of a mean n if the sample is a two-stage sample using random sampling with replacement at either stage or if the sampling fractions are so low that the difference between sampling with and sampling without replacement is negligible.

Effect for estimation of a mean n n n Since considerations for the choice of a design always are of an approximate nature, only those designs are considered here where each level-two unit contains the same number of level-one units. Level-two units will sometimes be referred to as clusters. The number of level-two units is denoted N The number of level-one units within each level-two unit is denoted n These numbers are called the level-two sample size and the cluster size, respectively The total sample size is Nn. If in reality the number of level-one units fluctuates between level -two units, it will almost always be a reasonable approximation to use for n the average number of sampled level-one units per level -two unit.

Effect for estimation of a mean n Suppose that the mean is to be estimated of some variable Y in a population which has a two-level structure. As an example, Y could be the duration of hospital stay after a certain operation under the condition that there are no complications or additional health problems. Random Intercept

Effect for estimation of a mean 1. This increase in complexity permeates to regression, etc 2. This is a relatively simple model, more complex models lead to more complex calculations that require the calculation of large covariance matrices

Easier Case The effect of each level-2 unit is a constant (fixed), not a random variable Another alternative to this operation is to add a dummy variable for each individual

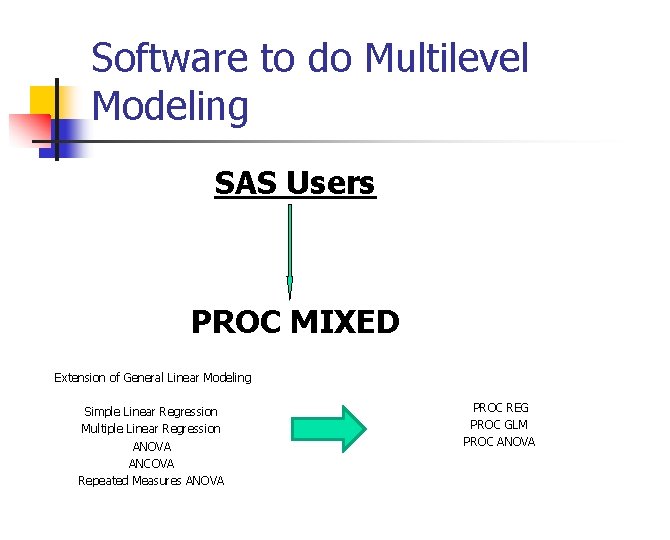
Software to do Multilevel Modeling SAS Users PROC MIXED Extension of General Linear Modeling Simple Linear Regression Multiple Linear Regression ANOVA ANCOVA Repeated Measures ANOVA PROC REG PROC GLM PROC ANOVA

Example: Family and Gender n n The response variable Height measures the heights (in inches) of 18 individuals. The individuals are classified according to Family and Gender data heights; input Family Gender$ Height @@; datalines; 1 F 67 1 F 66 1 F 64 1 M 71 1 M 72 2 F 63 2 F 67 2 M 69 2 M 68 2 M 70 3 F 63 3 M 64 4 F 67 4 F 66 4 M 67 4 M 69 ; run; Different than “Effects…” because now we have more cluster levels, but no random intercepts

Example: Family and Gender n n n The PROC MIXED statement invokes the procedure. The CLASS statement instructs PROC MIXED to consider both Family and Gender as classification variables. Dummy (indicator) variables are, as a result, created corresponding to all of the distinct levels of Family and Gender. For these data, Family has four levels and Gender has two levels. proc mixed data=heights; class Family Gender; model Height = Gender Family*Gender/s; run; s : requests that a solution for the fixed-effects parameters be produced along with their approximate standard errors

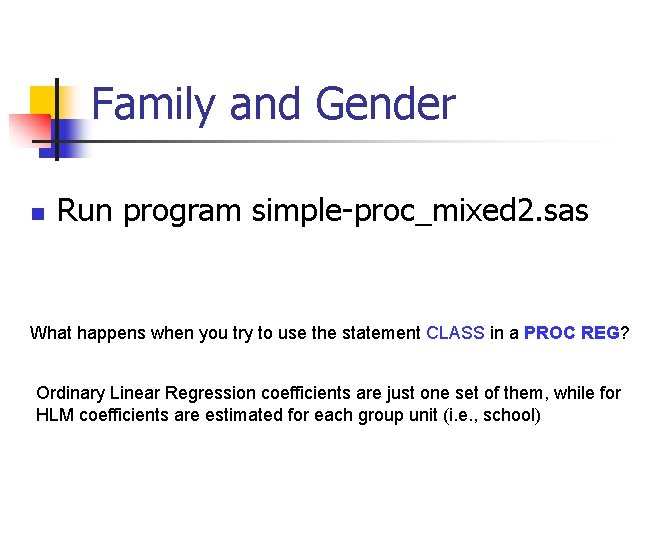
Family and Gender n Run program simple-proc_mixed 2. sas What happens when you try to use the statement CLASS in a PROC REG? Ordinary Linear Regression coefficients are just one set of them, while for HLM coefficients are estimated for each group unit (i. e. , school)

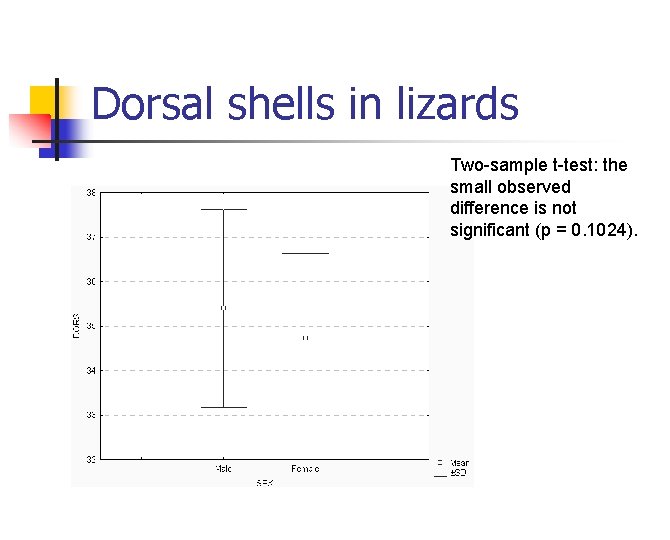
Dorsal shells in lizards Two-sample t-test: the small observed difference is not significant (p = 0. 1024).

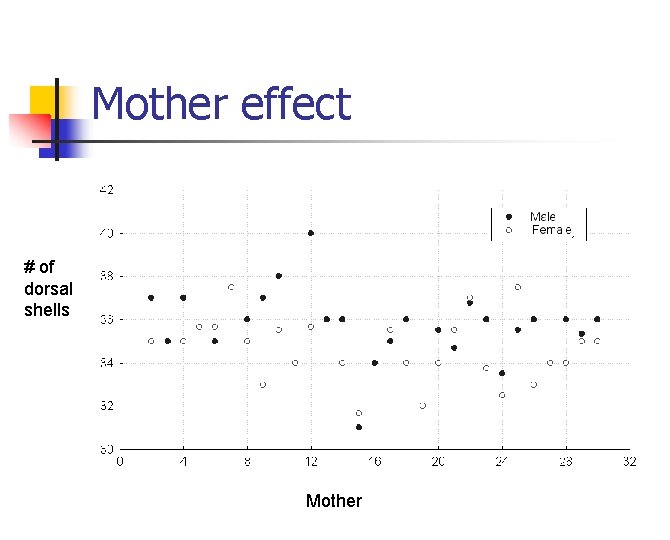
Mother effect n n n We have 102 lizards from 29 mothers Mother effects might be present Hence a comparison between male and female animals should be based on within-mother comparisons.

Mother effect # of dorsal shells Mother

First Choice Β can be interpreted as the average difference between males and females for each mother Test for a ‘sex’ effect, correcting for ‘mother’ effects, More complex example than “Effect…” because now we have a variable xij for each observation

Notice that in the previous example “Family and Gender” , gender was a used to define level(cluster) here is just a variable. In previous example it was assumed that individual of the same gender were “clustered”/correlated? Now it is just an input variable SAS program proc mixed data = lizard; class mothc; model dors = sex mothc; run; Source SEX MOTHC F Value 7. 19 3. 95 Pr > F 0. 0091 <. 0001 1. Highly significant mother effect. 2. Significant gender effect. 3. Many degrees of freedom are spent to the estimation of the mother effect, which is not even of interest

Later in this semester… n Note the different nature of the two factors: n n n SEX: defines 2 groups of interest MOTHER: defines 29 groups not of real interest. A new sample would imply other mothers. In practice, one therefore considers the factor ‘mother’ as a random factor. The factor ‘sex’ is a fixed effect. Thus the model is a mixed model. In general, models can contain multiple fixed and/or random factors. Fixed Effects Model Random Effects Model As in the slides of “Effect…”

Later in this semester… n Note the different nature of the two factors: n n n SEX: defines 2 groups of interest MOTHER: defines 29 groups not of real interest. A new sample would imply other mothers. In practice, one therefore considers the factor ‘mother’ as a random factor. The factor ‘sex’ is a fixed effect. Thus the model is a mixed model. In general, models can contain multiple fixed and/or random factors. proc mixed data = lizard; class mothc; model dors = sex / solution; random mothc; run;

More terminology n Fixed coefficient n n A regression coefficient that does not vary across individuals Random coefficient n A regression coefficient that does vary across individuals

Is a variable random or fixed effect? n n n La. Motte 1983, pp. 138– 139 Treatment levels used are the only ones about which inferences are sought => fixed Effect Inferences are sought about a broader collection of treatment effects than those used in the experiment, or if the treatment levels are not selected purposefully => Random Effect

More terminology n Balanced design n n Unbalanced design n n Unequal number of observation per unit Unconditional model n n Equal number of observations per unit Simplest level 2 model; no predictors of the level 1 parameters (e. g. , intercept and slope) Conditional model n Level 2 model contains predictors of level 1 parameters

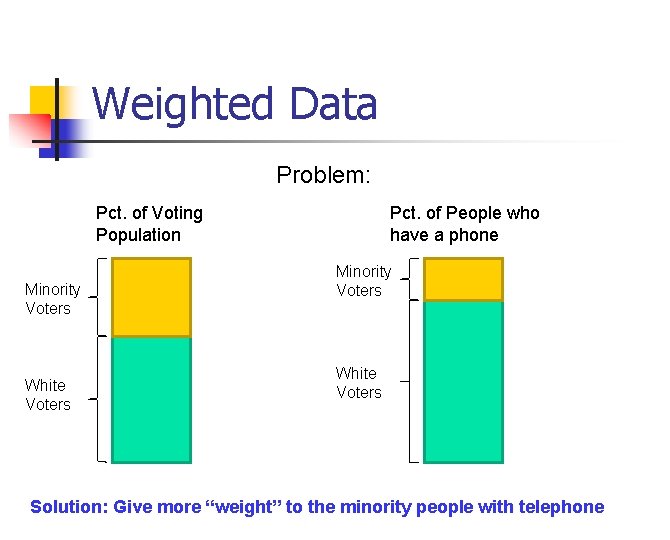
Weighted Data Problem: Pct. of Voting Population Minority Voters White Voters Pct. of People who have a phone Minority Voters White Voters Solution: Give more “weight” to the minority people with telephone

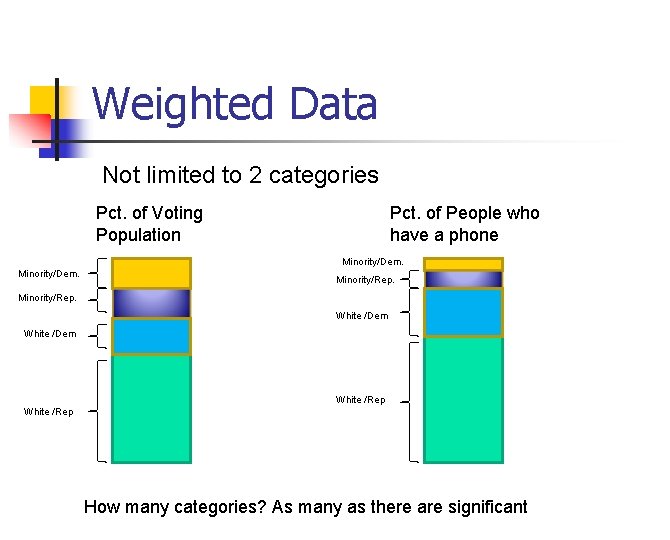
Weighted Data Not limited to 2 categories Pct. of Voting Population Pct. of People who have a phone Minority/Dem. Minority/Rep. White /Dem White /Rep How many categories? As many as there are significant

Proportion Suppose minority voters are 1/3 of the voting population but only 1/6 of the people with phone A sampling weight for a given data point is the number of receipts in the target population which that sample point represents. Needless to say that in reality this is a much more complex issue

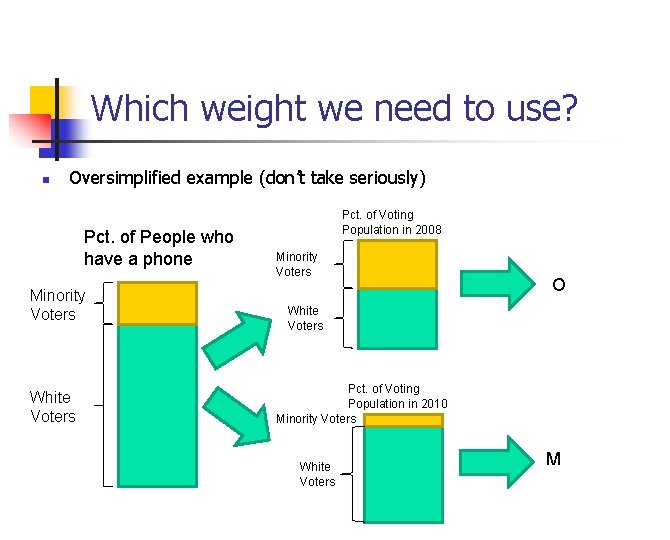
Which weight we need to use? n Oversimplified example (don’t take seriously) Pct. of People who have a phone Minority Voters White Voters Pct. of Voting Population in 2008 Minority Voters O White Voters Pct. of Voting Population in 2010 Minority Voters White Voters M

Proportion Suppose minority voters are 1/3 of the voting population but only 1/6 of the people with phone 1. 100 minority + 500 white answer the phone survey 2. 75 Minority will vote for candidate X 3. 250 White will votes for candidate X 4. Non-Weighted Conclusion: 325/600 =54. 16% of the voters will vote for candidate X 5. Weighted Conclusion: 1. 75 minority = 75% of minority with phone=>(. 75)*(1/6)=12. 5% of people with phone * 2 weight= 25% pct of voting population 2. 250 white = 50% of white people with phone =>(. 5)*(5/6)= 41. 66% of people with phone *. 8 weight =>33. 33% 3. 25% +33. 33%=58. 33%

SAS Weighted Mean proc means data=sashelp. class; var height; run; proc means data=sashelp. class; weight; var height; run;

Weighted PROC MIXED proc mixed data=sashelp. class covtest; class Sex; model height=Sex Age/solution; weight; run; Notice the difference (kind of small) in let’s say the coefficients of the model (Solution for Fixed Effects/Estimates)

Farms Example n n It's stratified by regions within Iowa and Nebraska. Regress on farm area, with separate intercept and slope for each state

References n La. Motte, L. R. (1983). Fixed-, random-, and mixed-effects models. In Encyclopedia of Statistical Sciences, S. Kotz, N. L. Johnson, and C. B. Read