Multilevel Hypergraph Partitioning Applications in VLSI Domain G

Multilevel Hypergraph Partitioning Applications in VLSI Domain G. Karypis, R. Aggarwal, V. Kumar, and S. Shekhar Computer Science Department, U of MN

Overview • • Problem definition Earlier work on partitioning Multilevel graph partitioning algorithms Multilevel hypergraph partitioning algorithms • Experimental results • Conclusion

Problem Definition • Given a hypergraph G = (V, E) we want to find a balanced bisection such that the number of hyperedges that are cut is minimized. • Applications 4 4 VLSI (packaging, synthesis, optimization, …) Numerical computations Transportation Data-mining

Overview of Partitioning Algorithms Effective partitioning algorithms must utilize both global as well as local information. Global View Knowing where to bisect Local View The ability to fine-tune a bisection A number of partitioning algorithms have been developed, utilizing global and local information to different degrees. Single-level Two-level Multi-level

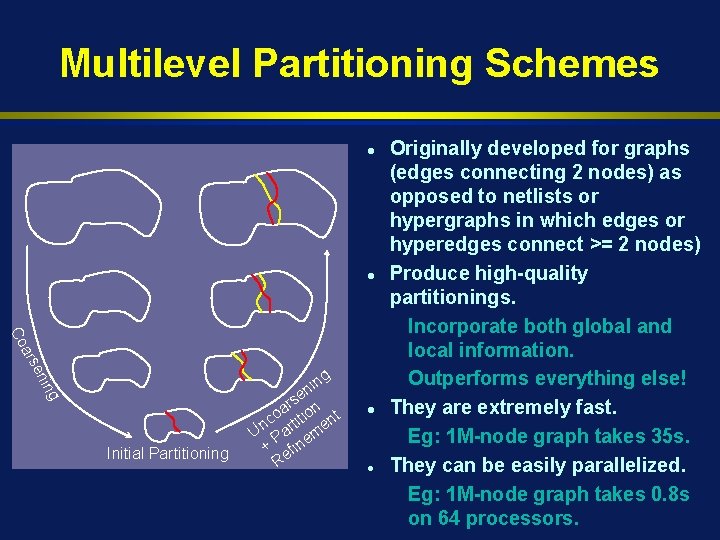
Multilevel Partitioning Schemes l l ars Co ing en Initial Partitioning n e rs n a co rtitio ent n U Pa em + fin Re l l Originally developed for graphs (edges connecting 2 nodes) as opposed to netlists or hypergraphs in which edges or hyperedges connect >= 2 nodes) Produce high-quality partitionings. Incorporate both global and local information. Outperforms everything else! They are extremely fast. Eg: 1 M-node graph takes 35 s. They can be easily parallelized. Eg: 1 M-node graph takes 0. 8 s on 64 processors.

Ingredients of Multilevel Partitioning Coarsening u u u Refinement Successive coarse graphs must make it easier to find a good partition. u u Initial Partitioning Uniform vertex weights (node/vertex “sizes” should be as uniform as possible). Exposed edge-weight must decrease rapidly. The `how to coarsen’ computation must be fast. The size of successive coarse graphs must decrease relatively fast u less time spent in coarsening, less memory.

Ingredients of Multilevel Partitioning Coarsening u u u Initial Partitioning This is the easiest of the three phases. Everything reasonable works fine. Random+FM, spectral, region growing, etc. It requires very little time Operates on small graphs (~100 vertices). Refinement

Ingredients of Multilevel Partitioning Coarsening u u u Initial Partitioning Refinement Needs a local partitioning refinement algorithm. Any vertex-swapping algorithm can be used KL, FM, etc. If coarsening is done correctly, simple refinement algorithms work extremely well and this phase requires very little time.

Metis: Multilevel Graph Partitioning u Coarsening u u u Maximal independent set of edges (matching). Preference to high weight edges: heavy-edge. Effective in reducing the exposed edge-weight! u Initial u Partitioning A region-growing followed by FM u Refinement u 2 2 1 A simplified version of FM Only up to 4 passes, Early exit u Very fast refinement. Metis is an extremely fast, robust, high-quality graph partitioning algorithm.

Going from Graphs to Hypergraphs • Hypergraph partitioning is significantly more complicated than graph partitioning. • Just look at the various refinement algorithms used in hypergraphs. n n Graphs: KL/FM Hypergraphs: KL/FM, LA, PROP, CLIP, etc. Can we find proper coarsening schemes that will let us use simple and fast refinement schemes and get good and robust performance?

Hypergraph Coarsening Schemes • Edge-based coarsening schemes n 4 8 Pairs of connected vertices are collapsed together, using the heavy-edge heuristic. Easy and fast to compute. Does not dramatically decrease the exposed hyperedge weight. u 8 Requires a lot of refinement in order to obtain good partitionings u 8 Cannot easily remove moderate-size hyperedges. Requires sophisticated refinement schemes Can lead to good partitionings but very slow!

Hypergraph Coarsening Schemes • Hyperedge-based coarsening schemes Collapses together all the vertices of an entire hyperedge. n Preference is given to the heavier hyperedges. 4 Easy and fast to compute. 4 It dramatically decreases the exposed hyperedge weight. 4 Leads to very good initial partitionings. n u 3600 as opposed to 6200 for golem 3! Requires very little refinement time. 4 High-quality partitionings can be obtained with simple refinement schemes. 4

h. Metis: Multilevel Hypergraph Partitioning Algorithm • Uses hyperedge-based coarsening. • Uses a simplified version of FM for refinement n Limits the number of passes, Early-exit • Employs some new multilevel refinement techniques to further improve the quality. h. Metis is an extremely fast, robust, highquality hypergraph partitioning algorithm.

Experimental Setup • We used the ACM/SIGDA circuit partitioning benchmark. • Experiments were performed on a MIPS R 10000@200 Mhz. • Results represent a 45 -55 balance condition. • Best out of 20 runs using EE-FM and multilevel refinement.

Bisection Quality

Bisection Runtime

Conclusions • The multilevel paradigm with the right coarsening and refinement scheme works extremely well for hypergraphs. • The quality of the partitionings can be further improved by running the algorithm multiple times. • h. Metis will be made available in the public domain by the end of June. URL: http: //www. cs. umn. edu/~karypis/metis