Multilevel Hierarchical Matrix Multiplication on Clusters Sascha Hunold

Multilevel Hierarchical Matrix Multiplication on Clusters Sascha Hunold Thomas Rauber Gudula Runger

Outline • Background • Introduction algorithm • Multilevel combination • Experiment result • Conclusion

Background • One of the core computations algorithms for scientific computing and numerical analysis.

Background • Many efficient realizations have been invented over the years, such as Strassen on distributed system and BLAS on single processor. • In this paper, different combinations of existing algorithms applying in the multilevel were investigated, and compared with the isolation algorithms.

Introduction algorithm • Strassen algorithm • Task parallel matrix multiplication(tp. MM) • PDGEMM

Strassen algorithm • Matrices A and B are of dimension with an even n, the matrix product can be expressed as: where Total 7 multiplications and 18 additions

Strassen algorithm Task C 11 compute Q 7 receive Q 5 Task C 12 compute Q 3 compute Q 5 send Q 5 Task C 21 compute Q 2 compute Q 4 send Q 2 Task C 22 compute Q 1 compute Q 6 receive Q 2 receive Q 4 send Q 3 send Q 4 receive Q 3 Time complexity O(n 2. 8) while recursive call Strassen for the distributed sub-blocks.

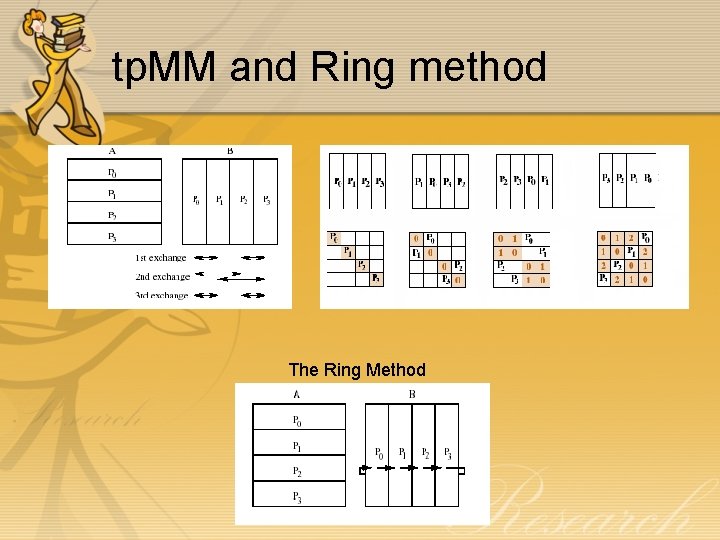
Task parallel matrix multiplication(tp. MM) • tp. MM is designed to work with processors which are groups into clusters. • The input matrices Amn and Bnk and p % m=0 and p % k=0. • The initial data distribution is a row block-wise distribution for matrix A and a column block-wise distribution for matrix B.

tp. MM and Ring method The Ring Method

PDGMM • Functions declaration from the Parallel Basic Linear algebra set(PBLAS) (part of the SCal. LAPACK project). • Exists numerous implementations, vendorspecific or free realizations as in Scal. APACK. • The algorithm that lies behind this function interface differs in most libraries. • Available on almost all parallel systems and becomes the de-facto standard for fast parallel matrix-matrix multiplication.

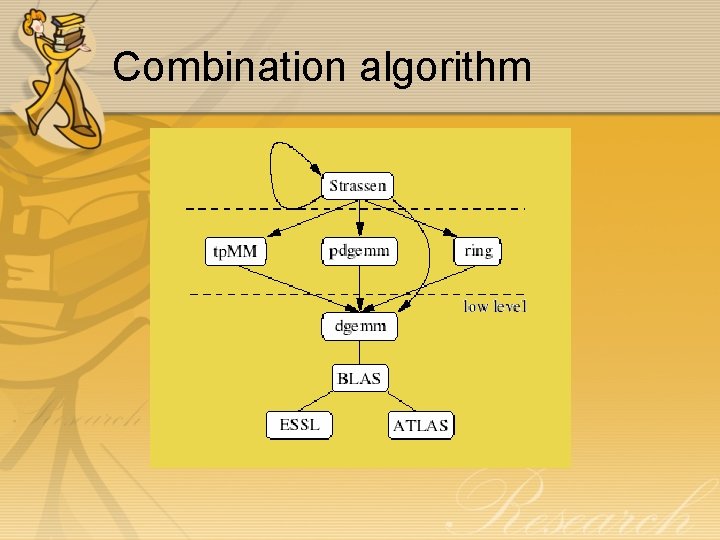
Combination algorithm

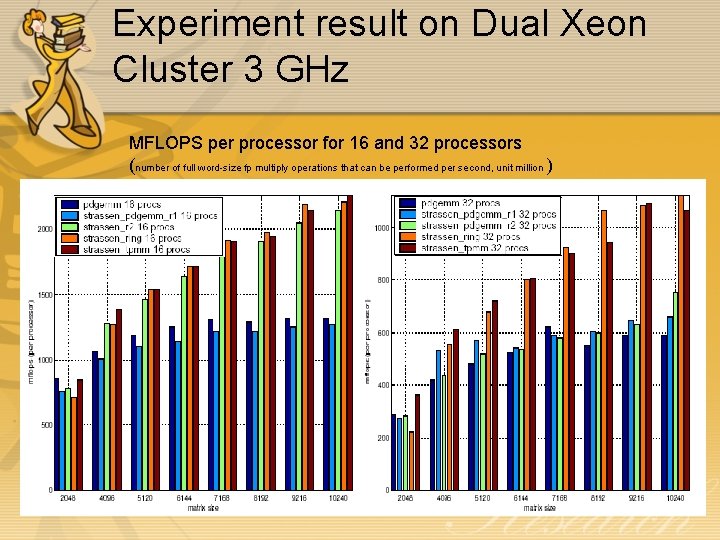
Experiment result on Dual Xeon Cluster 3 GHz MFLOPS per processor for 16 and 32 processors (number of full word-size fp multiply operations that can be performed per second, unit million )

Conclusion • Combination multilevel algorithms can get significant performance. • Important point for the construction of the multilevel algorithms is the order and block size. • Experiment shows that a combination Strassen’s method at top level with special communications-optimized algorithms on the intermediate level and ATLAS or DGEMM at the bottom level to the best results

Questions • Q&A