Multilevel Codes and Iterative Multistage Decoding M Jaber

Multilevel Codes and Iterative Multistage Decoding M. Jaber Borran and Behnaam Aazhang Rice University

Overview • Motivation – High rate communication in fading channels – Diversity gain and coding gain • Multilevel codes – Multistage decoding – Updated a priori probabilities • Concatenated space-time codes – Higher dimensional coded modulation
Motivation Fast fading environment
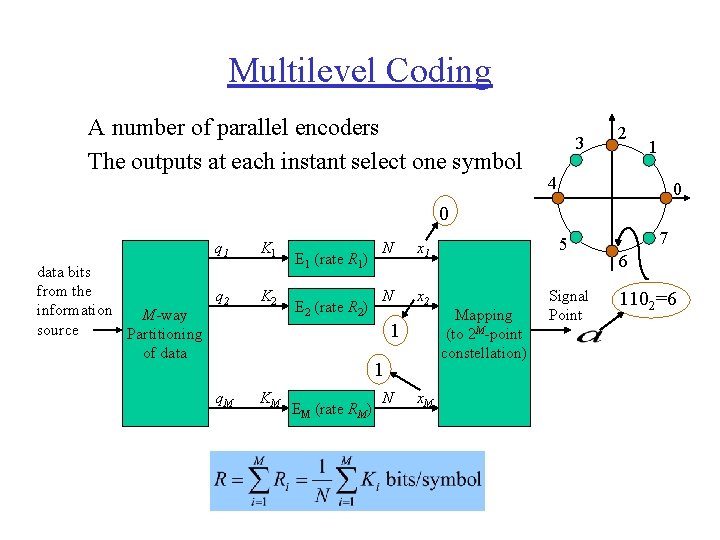
Multilevel Coding A number of parallel encoders The outputs at each instant select one symbol 3 2 1 4 0 0 q 1 data bits from the q 2 information M-way source Partitioning of data q. M K 1 K 2 E 1 (rate R 1) E 2 (rate R 2) N x 1 N x 2 1 1 KM EM (rate RM) N x. M 5 Mapping (to 2 M-point constellation) Signal Point 7 6 1102=6

Distance Properties • Minimum Hamming distance for encoder i: d. Hi , Minimum Hamming distance for symbol sequences • For TCM (because of the parallel transitions) d. H = 1 • MLC is a better candidate for coded modulation over fast fading channels

Decoding • Optimum decoder: Maximum-Likelihood decoder • If the encoder memories are n 1, n 2, …, n. M, the total number of states is 2 n, where n = n 1 + n 2 + … + n. M. • Complexity Need to look for suboptimum decoders
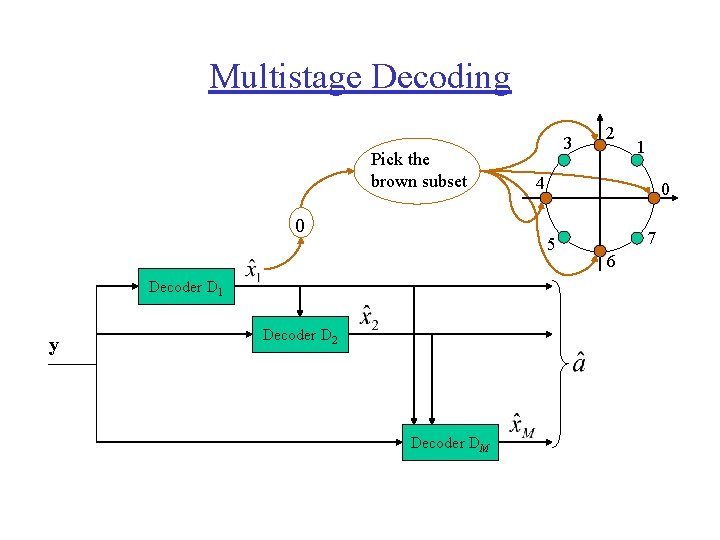
Multistage Decoding Pick the brown subset 0 Decoder D 2 Decoder DM 2 1 4 0 5 Decoder D 1 y 3 7 6
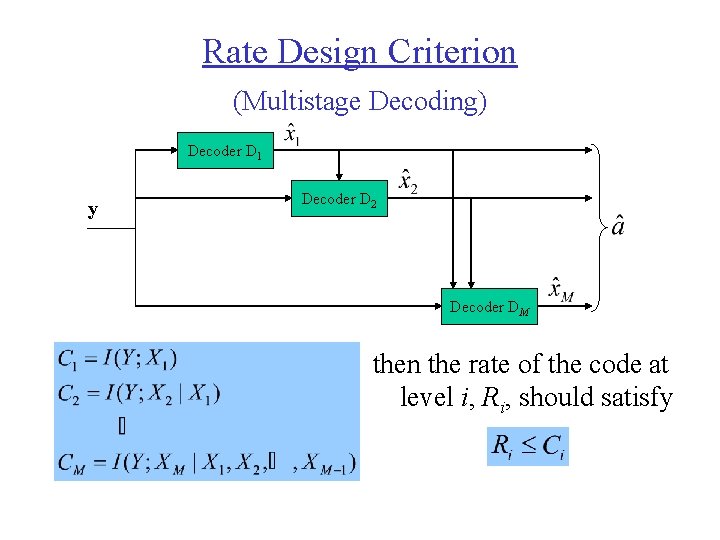
Rate Design Criterion (Multistage Decoding) Decoder D 1 y Decoder D 2 Decoder DM then the rate of the code at level i, Ri, should satisfy
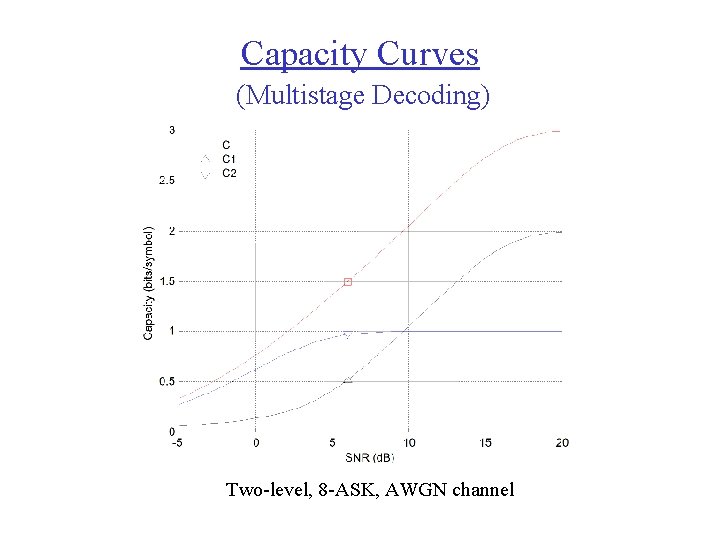
Capacity Curves (Multistage Decoding) Two-level, 8 -ASK, AWGN channel
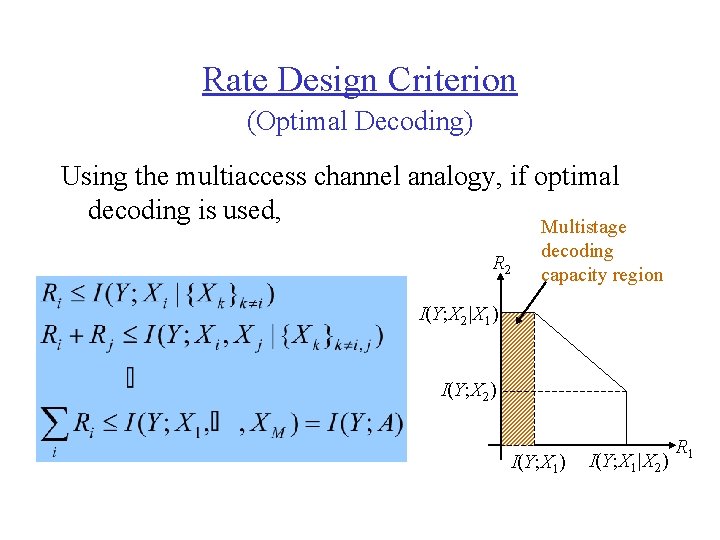
Rate Design Criterion (Optimal Decoding) Using the multiaccess channel analogy, if optimal decoding is used, Multistage R 2 decoding capacity region I(Y; X 2|X 1) I(Y; X 2) I(Y; X 1|X 2) R 1
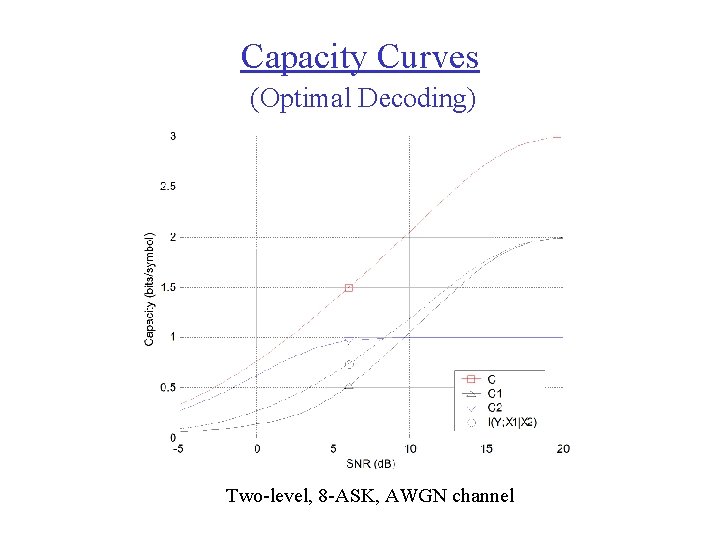
Capacity Curves (Optimal Decoding) Two-level, 8 -ASK, AWGN channel

Iterative Multistage Decoding • Approximating the optimum decoding • Assuming – Two level Code – R 1 I(Y; X 1|X 2) – Decoder D 1: then the a posteriori probabilities are This expression, then, can be used as a priori probability of point a for the second decoder.
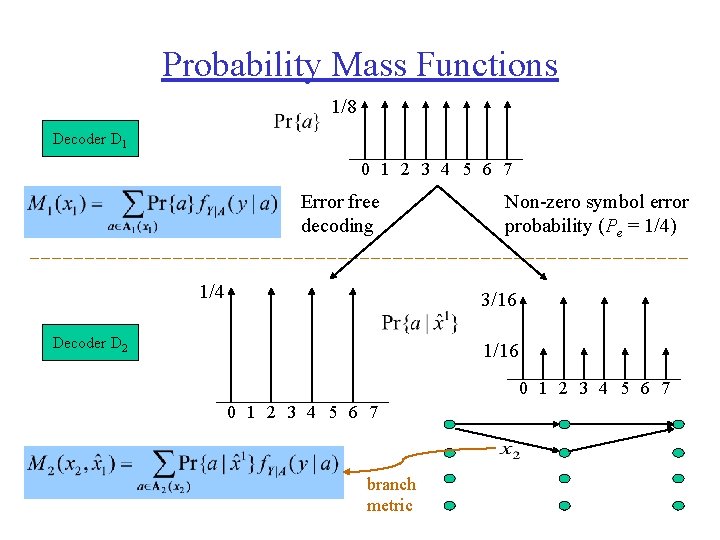
Probability Mass Functions 1/8 Decoder D 1 0 1 2 3 4 5 6 7 Error free decoding 1/4 Non-zero symbol error probability (Pe = 1/4) 3/16 Decoder D 2 1/16 0 1 2 3 4 5 6 7 branch metric
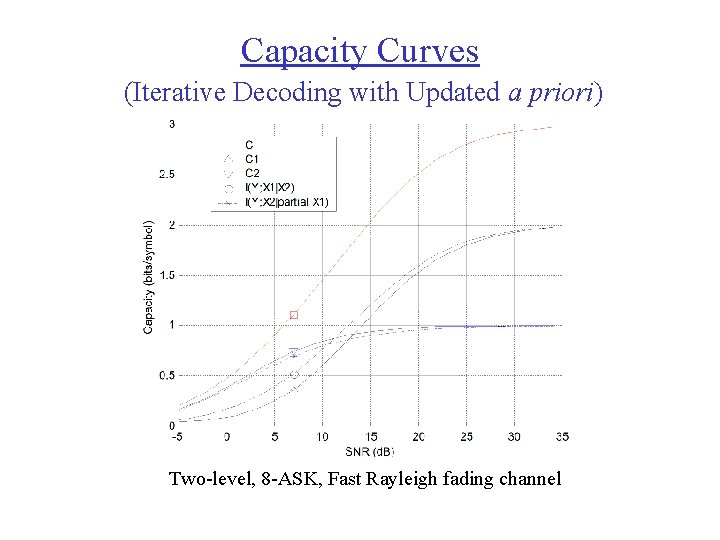
Capacity Curves (Iterative Decoding with Updated a priori) Two-level, 8 -ASK, Fast Rayleigh fading channel
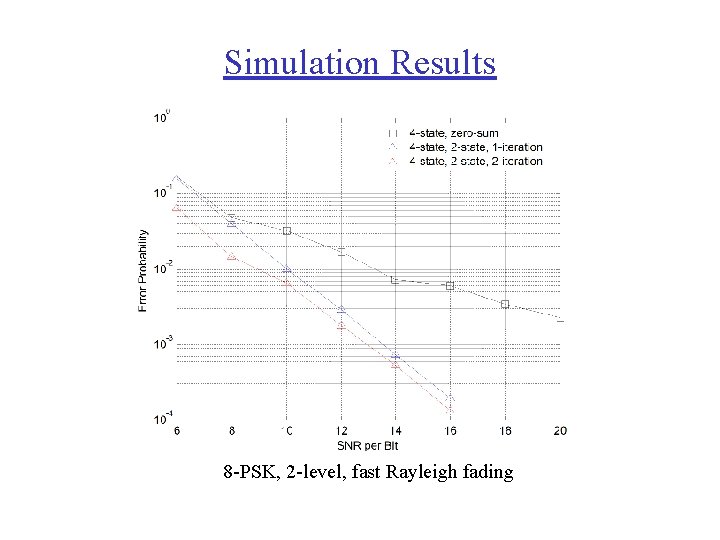
Simulation Results 8 -PSK, 2 -level, fast Rayleigh fading
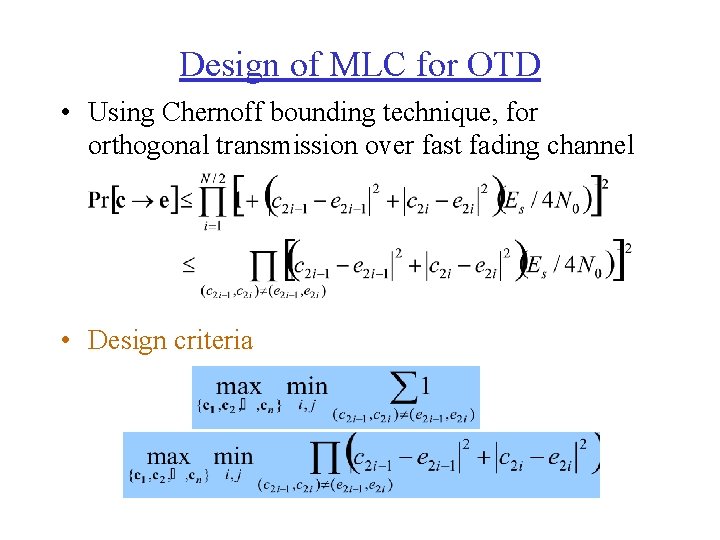
Design of MLC for OTD • Using Chernoff bounding technique, for orthogonal transmission over fast fading channel • Design criteria
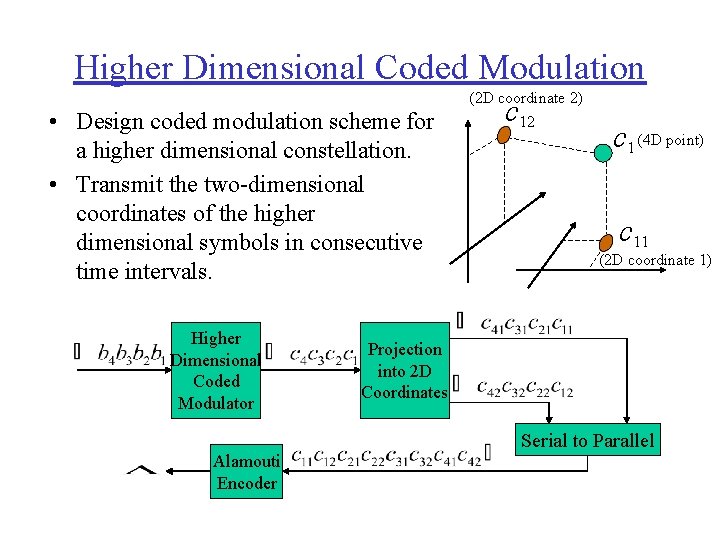
Higher Dimensional Coded Modulation • Design coded modulation scheme for a higher dimensional constellation. • Transmit the two-dimensional coordinates of the higher dimensional symbols in consecutive time intervals. Higher Dimensional Coded Modulator (2 D coordinate 2) 12 c c 1 (4 D point) c 11 (2 D coordinate 1) Projection into 2 D Coordinates Serial to Parallel Alamouti Encoder
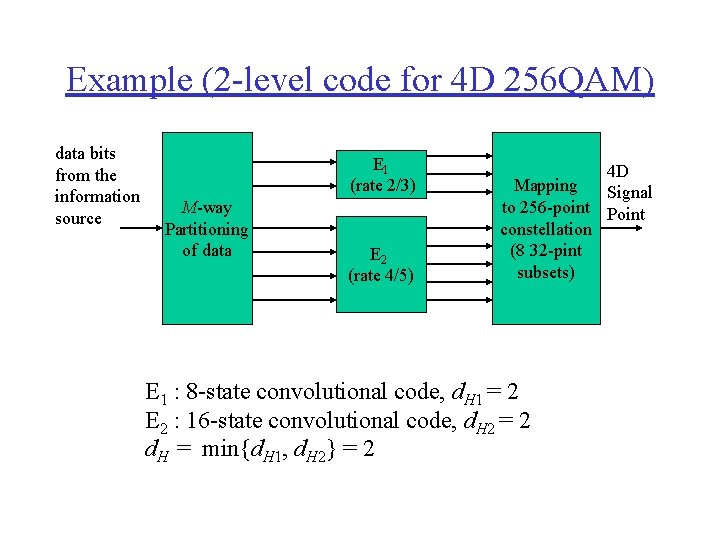
Example (2 -level code for 4 D 256 QAM) data bits from the information source E 1 (rate 2/3) M-way Partitioning of data E 2 (rate 4/5) 4 D Mapping Signal to 256 -point Point constellation (8 32 -pint subsets) E 1 : 8 -state convolutional code, d. H 1 = 2 E 2 : 16 -state convolutional code, d. H 2 = 2 d. H = min{d. H 1, d. H 2} = 2
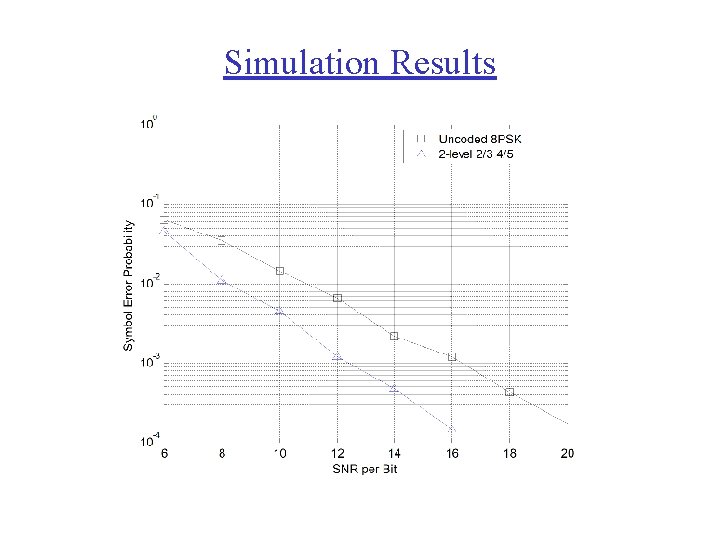
Simulation Results

Conclusions • Using iterative MSD with updated a priori probabilities, a broader sub-region of the capacity region of the MLC can be achieved. • MLC with iterative MSD and updated a priori probabilities can achieve better performance compared to regular MSD. • Higher dimensional constellations can be used to design MLC for OTD. As a result, temporal diversity can be traded off for coding gain.
- Slides: 20