Multigrid Algorithms for QCD Richard C Brower Mike

Multi-grid Algorithms for QCD Richard C. Brower (Mike Clark, James Brannick, Claudio Rebbi et al) CCS, University of Tsukuba March 10 , 2009 Future Code distribution at: http: //www. usqcd. org/software. html

Outline I. Failure of attempts in 1990’s : Why? II. Motivation and Current Progress III. Adaptive Multigrid – Wilson Dirac MG Algorithm IV. Discussion of Future Directions – – – Success of Adaptive GM: Why? Prune content of Null Space Actions: Domain Wall/Staggered MG Applications: Variance Reduction, RHMC Software Tools: Multi-level QMG API, ILDG – Consequence for GPGPU (see Clark’s talk)�

Failure of attempts in 1990’s : Why? – Partial success (RG) weak coupling – Maintain Gauge invariance – Maintain ° 5 Hermiticity – Learn from Failure

I. Early QCD attempts: See Thomas Kalkretuer hep-lat/9409008 review on “MG Methods for Propators in LGT”. Israel: Ben-Av, M. Harmatz, P. G. Lauwers & S. Solomon Boston: Brower, Edwards, Rebbi & Vicari Amsterdam: A. Hulsebos, J Smit J. C. Vick Hamburg: T. Kalkreuter, G. Mack & M. Speh

y R. C. Brower, R. Edwards, C. Rebbi, and E. Vicari, "Projective multigrid for. Wilson fermions", Nucl. Phys. B 366 (1991) 689 (aka Spectral AMG, Tim Chatier, 199? )

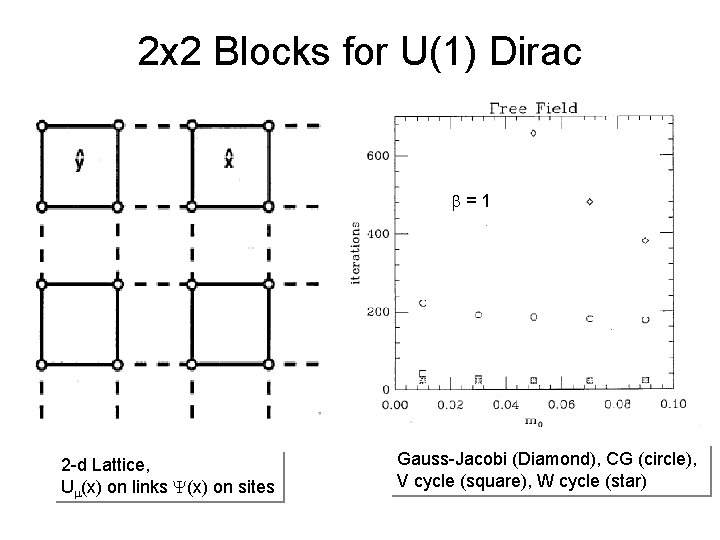
2 x 2 Blocks for U(1) Dirac =1 2 -d Lattice, U (x) on links (x) on sites Gauss-Jacobi (Diamond), CG (circle), V cycle (square), W cycle (star)

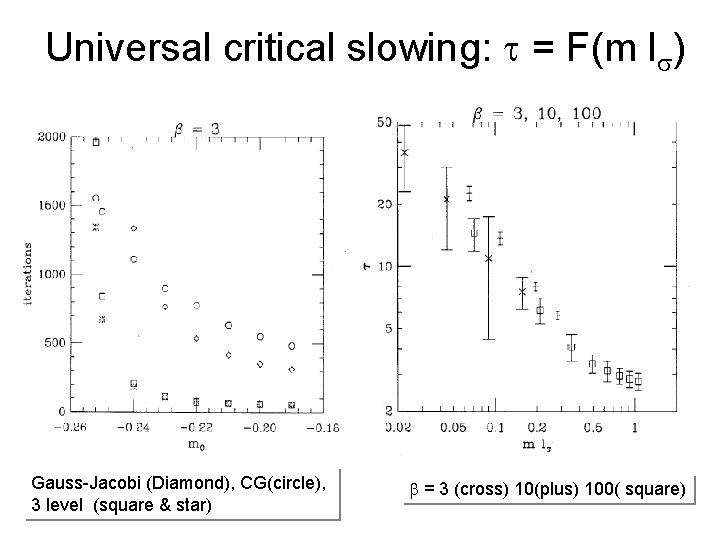
Universal critical slowing: = F(m l ) Gauss-Jacobi (Diamond), CG(circle), 3 level (square & star) = 3 (cross) 10(plus) 100( square)

Instantons, Confinement length l l Derek Leinweber http: //www. physics. adelaide. edu. au/~dleinweb/Visual. QCD/Nobel/index. html

II. Motivation and Current Progress

Higher resolution QCD • Lattice scales: – a(lattice) << 1/Mproton << 1/m¼ << L (box) – 0. 06 fermi << 0. 2 fermi << 1. 4 fermi << 6. 0 fermi 3. 3 x • Consequences: 7 x 4. 25 ' 100 – Increasing ill-conditioned Dirac operator – Suffer from worse critical slowing down (CSD) – O(100^4) lattice volume – 1/4 Terabyte file for a single Dirac propagator

Improved Dirac Inverters • Little progress in last 20 years? – Red-black preconditioning • (De. Grand 1988) • But recent progress (now that it’s needed!) – Eigenvector Deflation • (Morgan/Wilcox, Orginos/Stathopoulos) – Inexact Deflation + Schwarz Domain Decomp. • (Lüscher) – Adaptive Multi-grid • (BU/TOPS)

BU Applied Math/Physics Collaboration! Harvard U Mike Clark

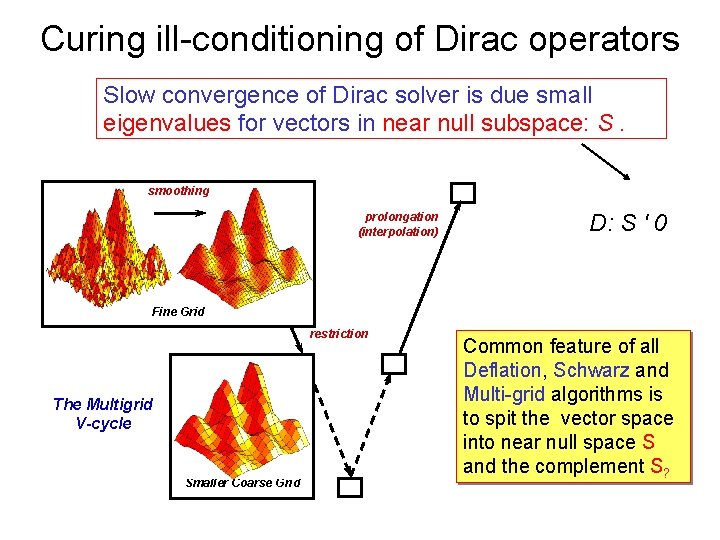
Curing ill-conditioning of Dirac operators Slow convergence of Dirac solver is due small eigenvalues for vectors in near null subspace: S. smoothing prolongation (interpolation) D: S ' 0 Fine Grid restriction The Multigrid V-cycle Smaller Coarse Grid Common feature of all Deflation, Schwarz and Multi-grid algorithms is to spit the vector space into near null space S and the complement S?

intro to multigrid: Laplace Operator Define the Prolongator P Define the Restriction operator R = P† Operator on coarse space

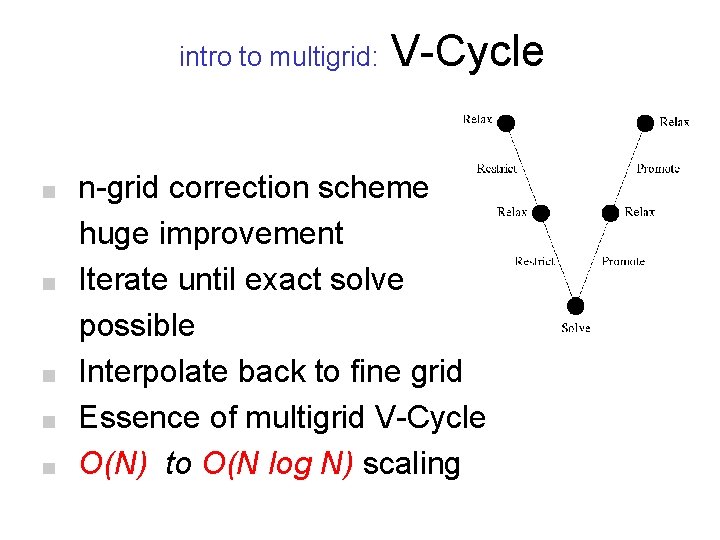
intro to multigrid: V-Cycle n-grid correction scheme huge improvement Iterate until exact solve possible Interpolate back to fine grid Essence of multigrid V-Cycle O(N) to O(N log N) scaling

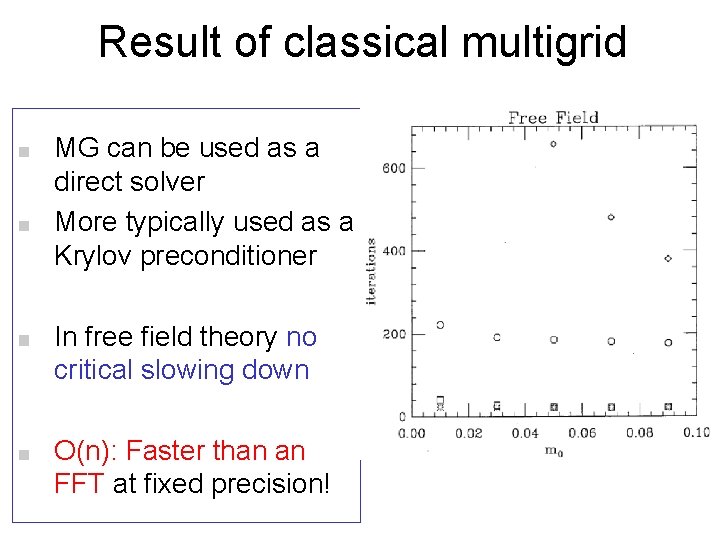
Result of classical multigrid MG can be used as a direct solver More typically used as a Krylov preconditioner In free field theory no critical slowing down O(n): Faster than an FFT at fixed precision!

General Problem: D à = b • “split” vector space into: – near null D S ' 0 & Complement S? • Schur decomposition (of course) does this! – Coarse = near null (IR) , Fine = complement (UV) Schur: Implies ��

Block solution to D Ã = b • Questions: • How to choose the splitting? • How to iterate to find Solution?

3 approaches to near null space 1. “Deflation”: Nº exact eigenvector projection 2. “Inexact deflation” plus Schwarz (Lüscher) 3. Multi-grid preconditioning Little Dirac: 1. Ze ro on co ar se s pa 2 & 3 use the same splitting S and S? ce

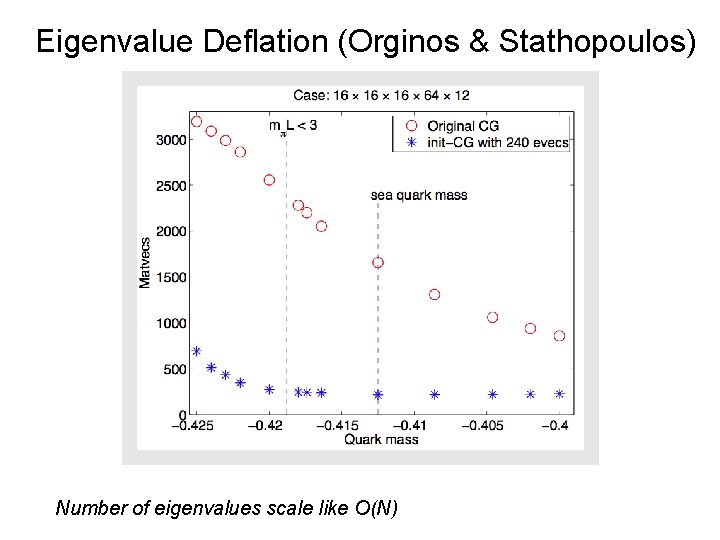
Eigenvalue Deflation (Orginos & Stathopoulos) Number of eigenvalues scale like O(N)

2 -level Multigrid Cycle (simplified) • Smooth: x’ = (1 - D) x + b • Project: D c = Py D P • A c ec = r Solve: • Prolongate e = P e_c • Update x’ = x + e �� ) r’ = (1 - D) r & rc = Py�� r ) ec = A-1 c Py r ) r’ = b -D(x + e) = [ 1 - D P (Py D P)-1 Py] r RESULT: D is preconditioned by M = P (Py D P)-1 Py M-1 D x = M-1 b ) r’ = ( 1 - D M-1 ) r Note since Py r’ = 0 ) full (exact) deflation on S

Choosing the Prolongator (P) and Restrictor (R = Py) ? Relax from random vector to find near null vectors. Cut up on sublattice in Blocks of size 4 d d=2 for d=1, s =1 P= Ã1 Ã2 Ã3 Ã4 0 0 Ã5 Ã6 Ã7 Ã8. . . 0 0 0 . . . .

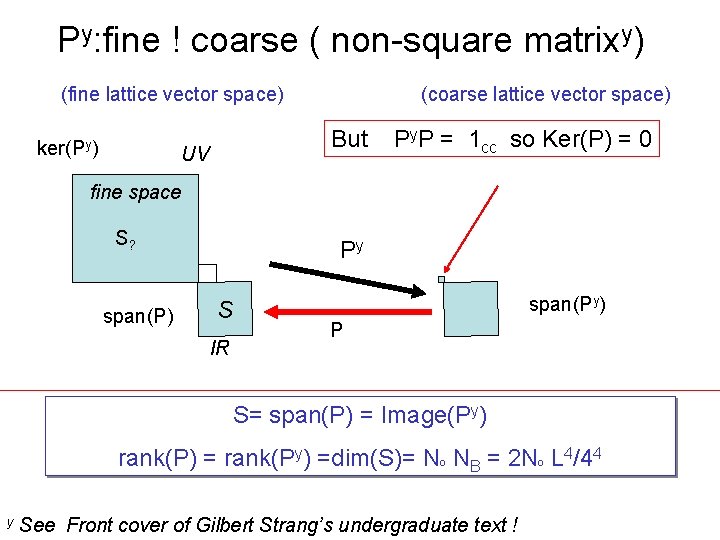
Py: fine ! coarse ( non-square matrixy) (fine lattice vector space) ker(Py) (coarse lattice vector space) But UV Py. P = 1 cc so Ker(P) = 0 fine space S? span(P) Py S IR span(Py) P S= span(P) = Image(Py) rank(P) = rank(Py) =dim(S)= Nº NB = 2 Nº L 4/44 y See Front cover of Gilbert Strang’s undergraduate text !

Oblique Projector Algebra of splitting But P 2 ≠ P is not a “proper projection operator” -The projectors operator (¦ 2 = ¦ ) are: Lüscher’s “oblique” projectors are: PL = 1 - ¦y. L and PR = 1 - ¦R

• Real algorithm has lots of tuning! – MG proofs only for normal equation (Dy D Ã = b) – Multigrid is recursive to multi-levels. – – Near null vectors Ãsx found recursive use of MG itself. Preserves ° 5 ( [° 5, P]= 0) and Gauge invariance pre and post-smoothing is done by Minimum Residual. Entire cycle is used as preconditioner in CG • Current benchmarks for Wilson-Dirac: – – – V=163 x 32, β=6. 0, mcrit = 0. 8049, 4 Coarse lattice Block = 4 x Nc x 2, Nº =20. 3 level V(2, 2) MG cycle. 1 CG application per 6 Dirac application Note Nº scales O(1) but deflation Nº = O(V) Reducing Nº by pruning

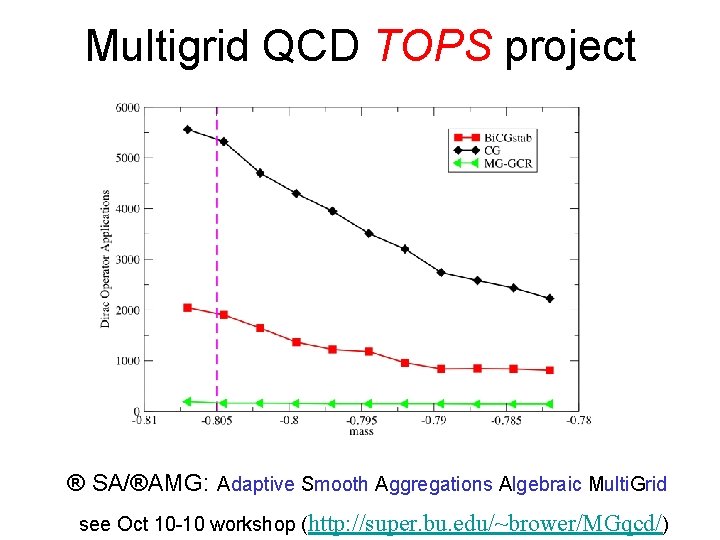
Multigrid QCD TOPS project ® SA/®AMG: Adaptive Smooth Aggregations Algebraic Multi. Grid see Oct 10 -10 workshop (http: //super. bu. edu/~brower/MGqcd/)

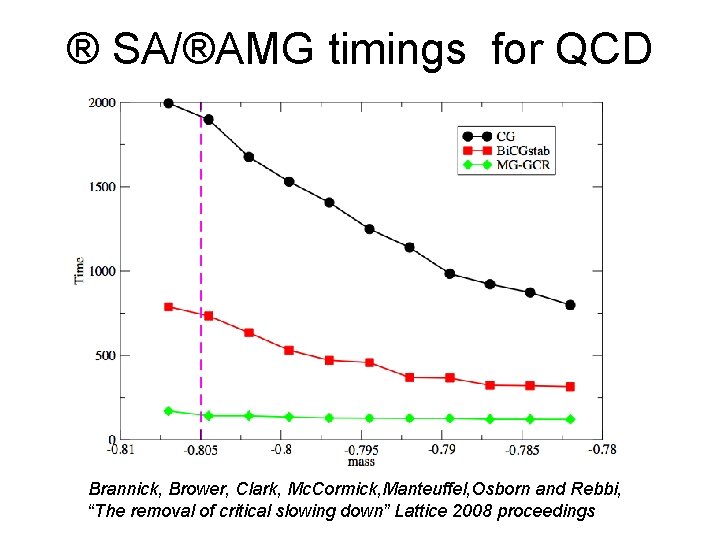
® SA/®AMG timings for QCD Brannick, Brower, Clark, Mc. Cormick, Manteuffel, Osborn and Rebbi, “The removal of critical slowing down” Lattice 2008 proceedings

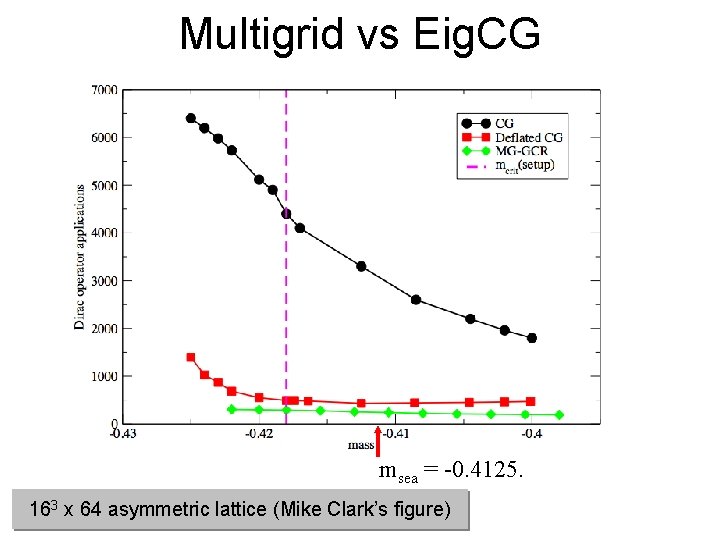
Multigrid vs Eig. CG msea = -0. 4125. 163 x 64 asymmetric lattice (Mike Clark’s figure)

IV. Discussion of Future Directions – Success of Adaptive GM: Why? – Prune content of Null Space – Other Lattice Actions • Domain Wall (or Overlap ? ) w. Scott Machachlan at Tufts • Staggered w. Carleton Detar and Mehmet Okay at Utah – Applications: • Multiple RHS (all to all/disconnected) • Variance Reduction (BU disco project • RHMC (see Luscher)

Instantons, Topological Zero Modes (Atiyah-Singer index) and Confinement length l l

Physics: Disconnected Diagrams Connected vs. Disconnected Want matrix element: 31

How strangey is the proton? Who cares? • Violation of Standard Model: – Dark Energy (Neutralino scattering): – Nu. Tev anomaly: • Nucleon Physics (include u/d + s quarks): – iso-scalar Form Factors, nucleon structure function, – Spin crisis for proton, matrix element etc. y see Lattice 2008: Ohki et al Lattice plenary talk. S. Collins, G. Bali, A. Schafer “Hunting for the strangeness. . . nucleon” Takumi Doi et al Ron Babich et al “Strangeness and glue in the nucleon from lattice QCD “Strange quark content of the nucleon”

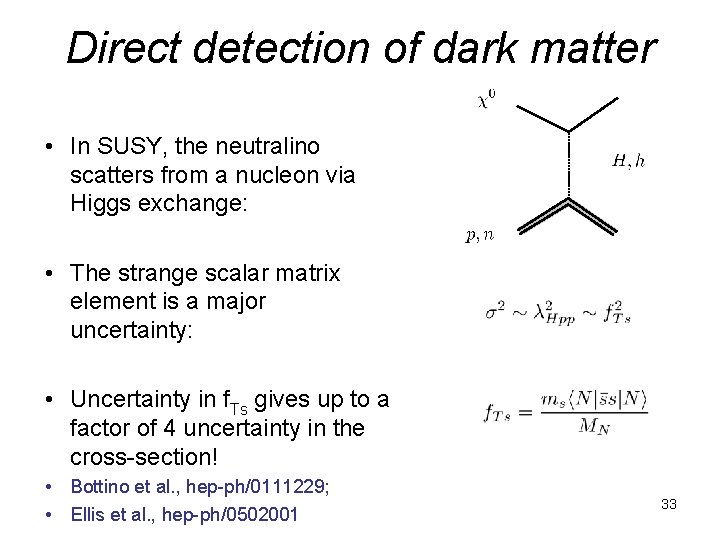
Direct detection of dark matter • In SUSY, the neutralino scatters from a nucleon via Higgs exchange: • The strange scalar matrix element is a major uncertainty: • Uncertainty in f. Ts gives up to a factor of 4 uncertainty in the cross-section! • Bottino et al. , hep-ph/0111229; • Ellis et al. , hep-ph/0502001 33

Multi-grid Variance Reduction • The signal and variance of the first term is down by 1 to 2 orders of magnitude because Dc » D • The Coarse level Trace for D-1 c is as cheap to calculate as the level down operator inverse. • This can of course be done recursively giving an O(N log N) trace calculation to fixed tolerance ?

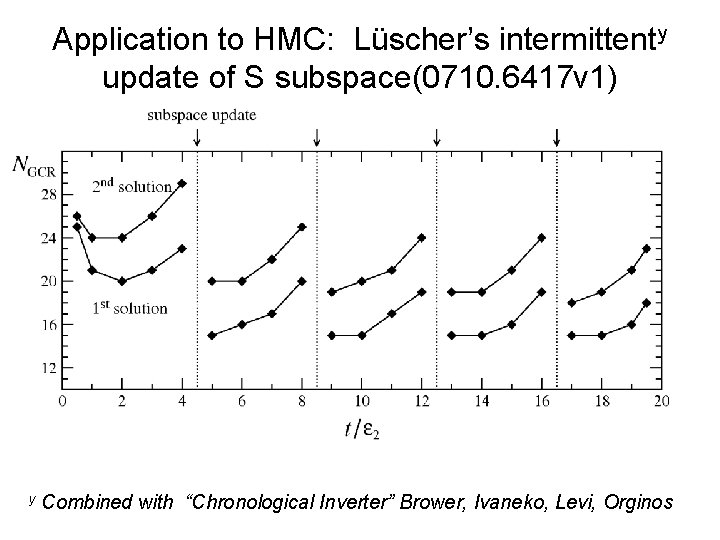
Application to HMC: Lüscher’s intermittenty update of S subspace(0710. 6417 v 1) y Combined with “Chronological Inverter” Brower, Ivaneko, Levi, Orginos

IV. More Future Directions – Software Tools: Multi-level Sci. DAC API • QMG w. James Osborn – ILDG • Store MG precondition with lattice? – Consequences for GPGPU • Mike Clark’s talk�

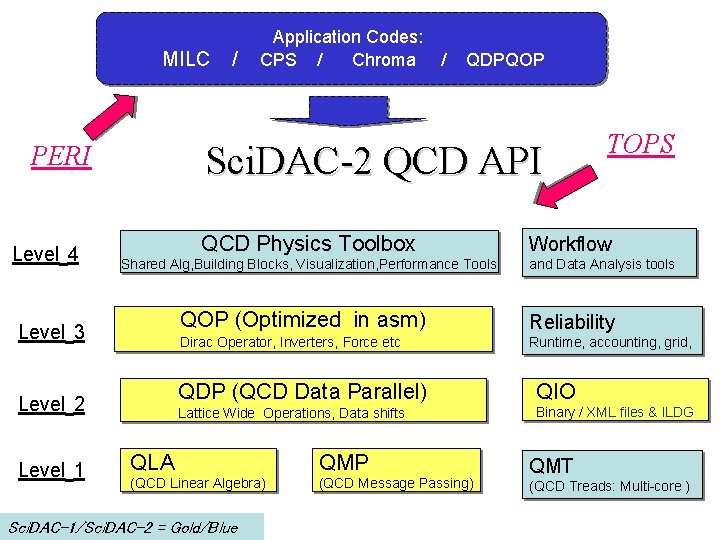
MILC QCD Physics Toolbox Shared Alg, Building Blocks, Visualization, Performance Tools QOP (Optimized in asm) Level 3 Dirac Operator, Inverters, Force etc Level 2 Level 1 QDPQOP Sci. DAC-2 QCD API PERI Level 4 / Application Codes: CPS / Chroma / TOPS Workflow and Data Analysis tools Reliability Runtime, accounting, grid, QDP (QCD Data Parallel) QIO Lattice Wide Operations, Data shifts Binary / XML files & ILDG QLA QMP (QCD Linear Algebra) (QCD Message Passing) Sci. DAC-1/Sci. DAC-2 = Gold/Blue QMT (QCD Treads: Multi-core )

Need Dirac Propagator Farm • The Clark-Kennedy RHMC Paradox: (Faster you go the harder it is to keep up) • Analysis is now the “Ἀχιλλεύς heel”

Nvidia Tesla Quad S 1070 1 U System $8 K Processors 4 x Tesla T 10 P Number of cores 960 Core clock 1. 5 Hz Performance 4 Teraflops memory BW 16. 0 GB bandwidth 408 GB/sec Memory I/0 2048 bit, 800 MHz Form factor 1 U (EIA 19” rack) System I/O 2 PCIe x 16 Gen 2 Typical power 700 W

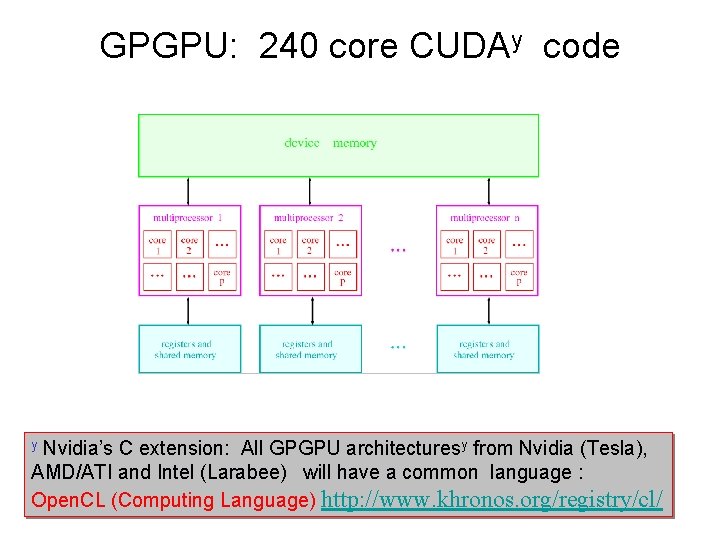
GPGPU: 240 core CUDAy code Nvidia’s C extension: All GPGPU architecturesy from Nvidia (Tesla), AMD/ATI and Intel (Larabee) will have a common language : Open. CL (Computing Language) http: //www. khronos. org/registry/cl/ y

Commercial Break: (QCDNA in Boston Fall 2009? )