MultiDimensional Scaling and MODELLER based Evolutionary Algorithms for

Multi-Dimensional Scaling and MODELLER based Evolutionary Algorithms for Protein Model Refinement Yan Chen Advisor: Yi Shang 12. 06. 2013

Motivation q q To obtain an accurate protein structure is important in bioinformatics Refinement is a step in the prediction process Refinement category added since CASP 8(2008), the category is drawing increasing attention In CASP 10, 7 out of 50 groups improved the quality of the starting models (though only 2 or 3 are significantly better) 2

Motivation q q q Most groups degrade the starting model more often than they improve it Improvements are still small even for the best groups The goal of the project: Exploring new ways to improve existing refinement techniques 3

Methods Developed in the Project q Three evolutionary algorithms for protein model refinement v MDS-based: takes a purely geometrical approach and generates model by combining the contact maps. v MODELLER-based: takes a statistical and energy minimization approach and uses the remodeling module in MODELLER program. v Hybrid: first generates models using the MDS-based method and then run them through the MODELLERbased method, aiming at combining the strength of both. 4

Outline Existing work q Foundations q Proposed Methods q Experimental Results q Conclusions q 5

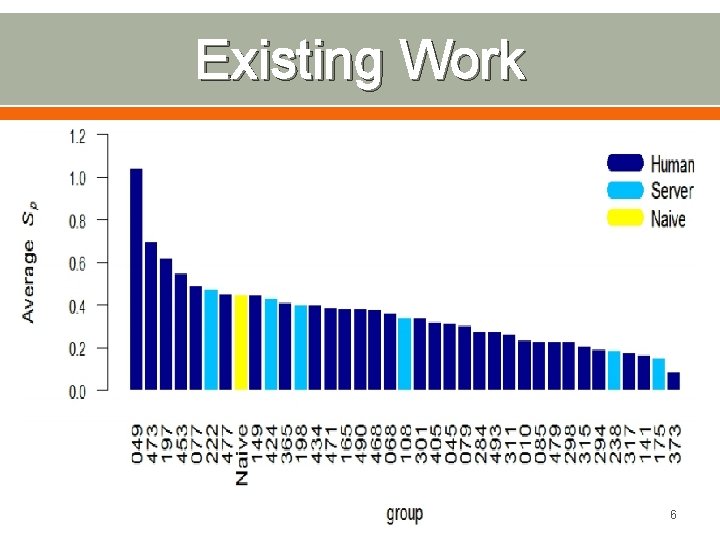
Existing Work 6

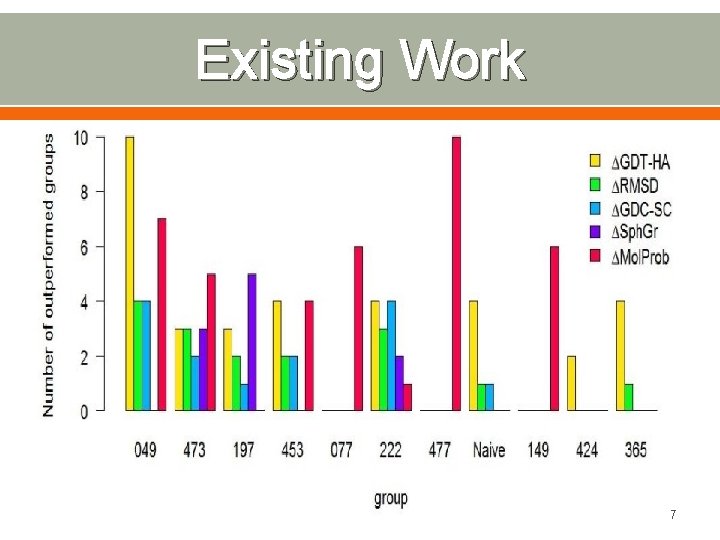
Existing Work 7

Outline Existing work q Foundations of the proposed methods q v Evolutionary Algorithm (EA) v Protein Quality Evaluation v MDS v MODELLER Proposed methods q Experimental Results q Conclusions q 8

Evolutionary Algorithm Start Initial population Evaluation En d Y Generation Cycle terminate? N Selection Crossover 9

Models Quality Assessment—CGDTTS q q Measure the correct positioning of amino acid sequences between two protein models Widely accepted as a QA tool in CASP 10

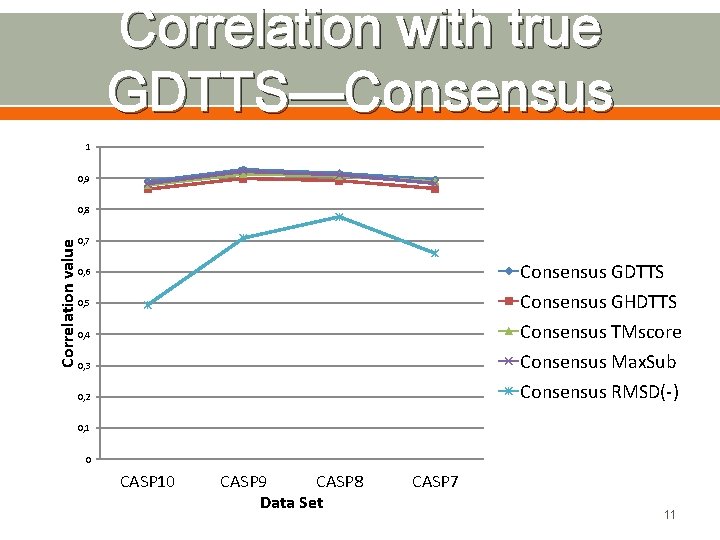
Correlation with true GDTTS—Consensus 1 0, 9 Correlation value 0, 8 0, 7 Consensus GDTTS Consensus GHDTTS Consensus TMscore Consensus Max. Sub Consensus RMSD(-) 0, 6 0, 5 0, 4 0, 3 0, 2 0, 1 0 CASP 10 CASP 9 CASP 8 Data Set CASP 7 11

Models Quality Assessment—Pro. Q 2 q Developed by B Wallner from Sweden in 2012 q Best single-model method in CASP 10 q Uses support vector machines to validate local and global quality of protein models 12

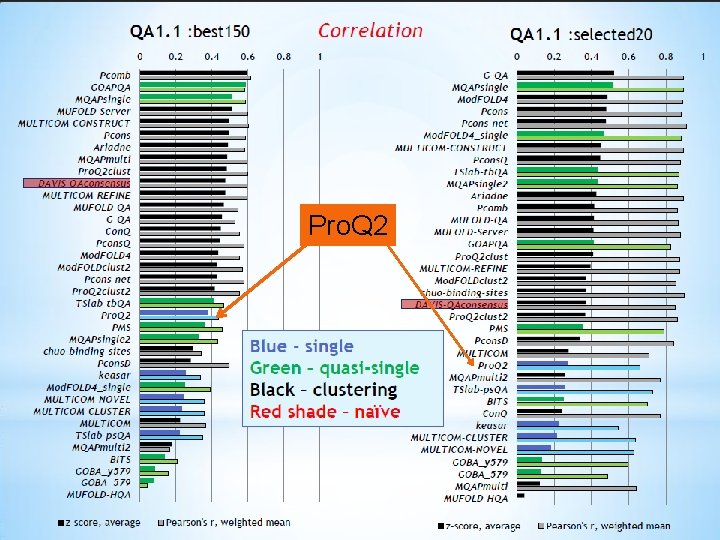
Pro. Q 2 13

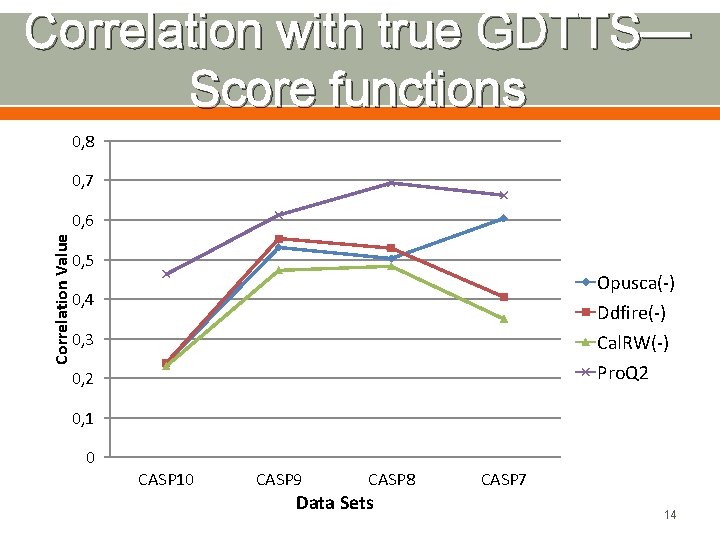
Correlation with true GDTTS— Score functions 0, 8 0, 7 Correlation Value 0, 6 0, 5 Opusca(-) Ddfire(-) Cal. RW(-) Pro. Q 2 0, 4 0, 3 0, 2 0, 1 0 CASP 10 CASP 9 CASP 8 Data Sets CASP 7 14

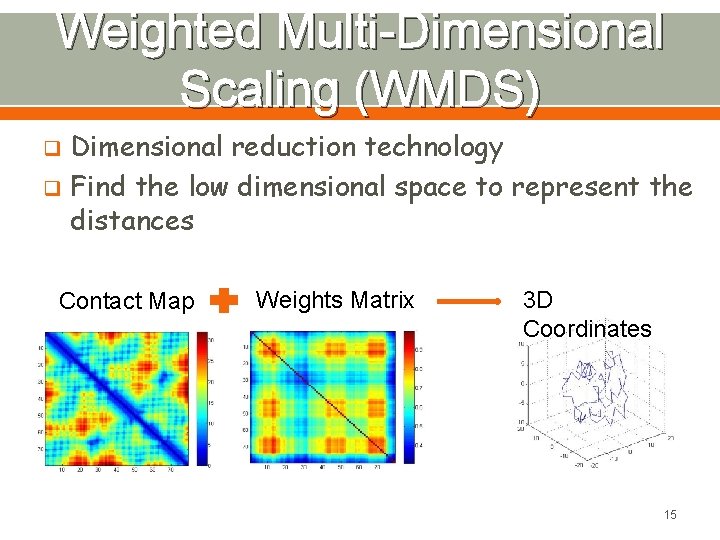
Weighted Multi-Dimensional Scaling (WMDS) Dimensional reduction technology q Find the low dimensional space to represent the distances q Contact Map Weights Matrix 3 D Coordinates 15

MODELLER Written by Andrej Sali at the University of California, San Francisco in 1993 q Used for homology or comparative modeling of protein three-dimensional structures q Sequence file <5 models Script file 3 D model 16

Outline Existing Work q Foundations q Proposed Methods q v Flow Chart v Generate Initial Population v Roulette Wheel Selection v Three Crossover Methods Experimental Results q Conclusions q 17

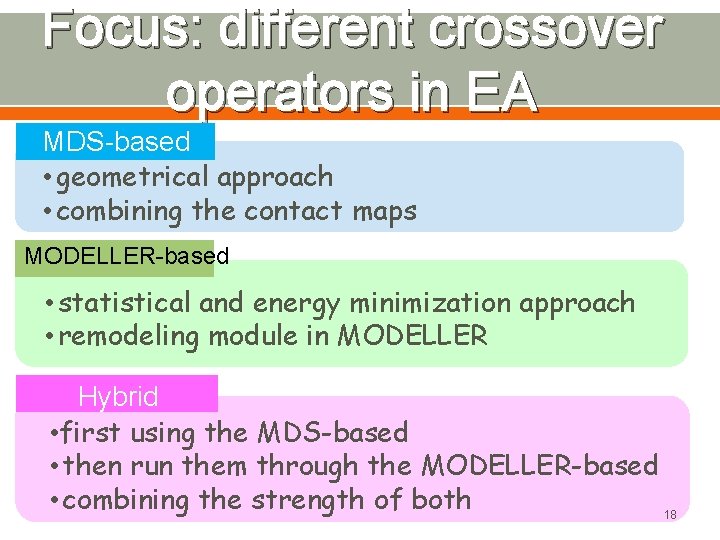
Focus: different crossover operators in EA MDS-based • geometrical approach • combining the contact maps MODELLER-based • statistical and energy minimization approach • remodeling module in MODELLER Hybrid • first using the MDS-based • then run them through the MODELLER-based • combining the strength of both 18

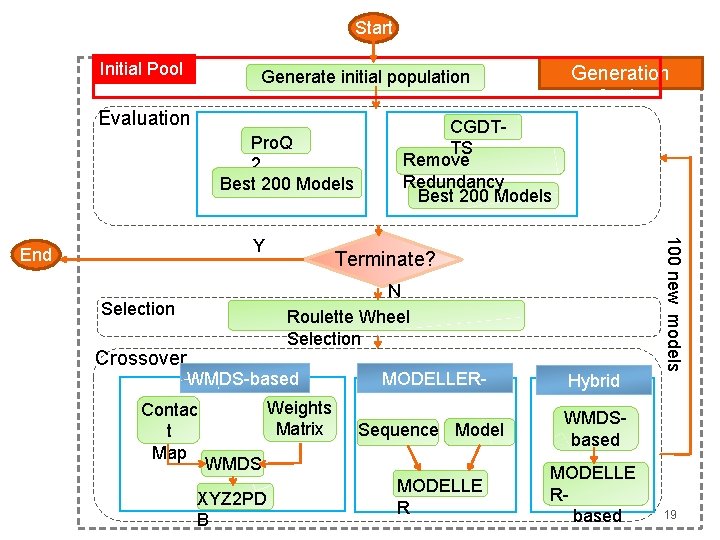
Start Initial Pool Evaluation Pro. Q 2 Best 200 Models CGDTTS Remove Redundancy Best 200 Models Terminate? N Roulette Wheel Selection WMDS-based Contac t Map Weights Matrix MODELLERbased Sequence Model WMDS XYZ 2 PD B MODELLE R Hybrid 100 new models Y End Crossover Generation Cycle Generate initial population WMDSbased MODELLE Rbased 19

Generate Initial Population q 20

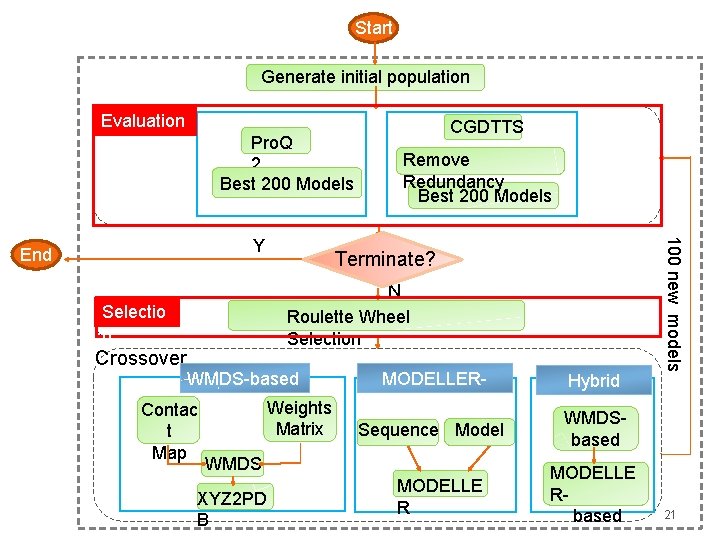
Start Generate initial population Evaluation Pro. Q 2 Best 200 Models Terminate? N Roulette Wheel Selection Selectio n Crossover Remove Redundancy Best 200 Models WMDS-based Contac t Map Weights Matrix MODELLERbased Sequence Model WMDS XYZ 2 PD B MODELLE R Hybrid 100 new models Y End CGDTTS WMDSbased MODELLE Rbased 21

Roulette Wheel Selection The most wildly used selection method q Based on the probability of individual q v The selection probability Pi for individual i where f 1, f 2, …, fn are the fitness values of individual 1, 2, …, n 22

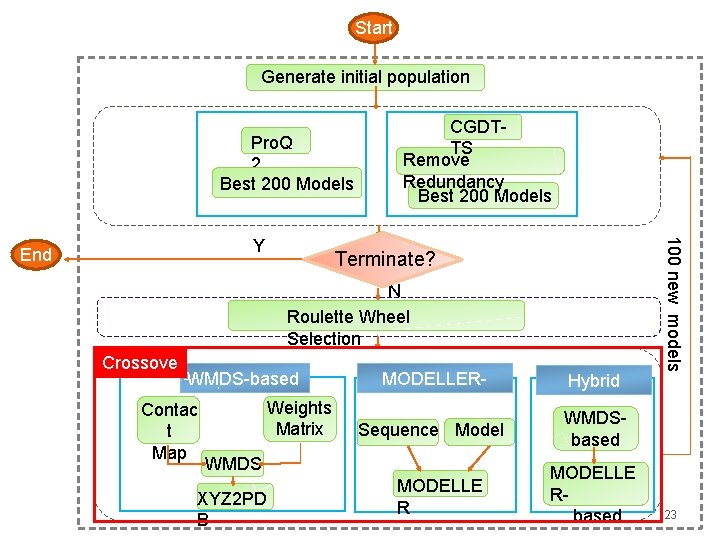
Start Generate initial population Pro. Q 2 Best 200 Models Y Terminate? N Roulette Wheel Selection Crossove WMDS-based r Weights Contac Matrix t Map WMDS XYZ 2 PD B MODELLERbased Sequence Model MODELLE R Hybrid 100 new models End CGDTTS Remove Redundancy Best 200 Models WMDSbased MODELLE Rbased 23

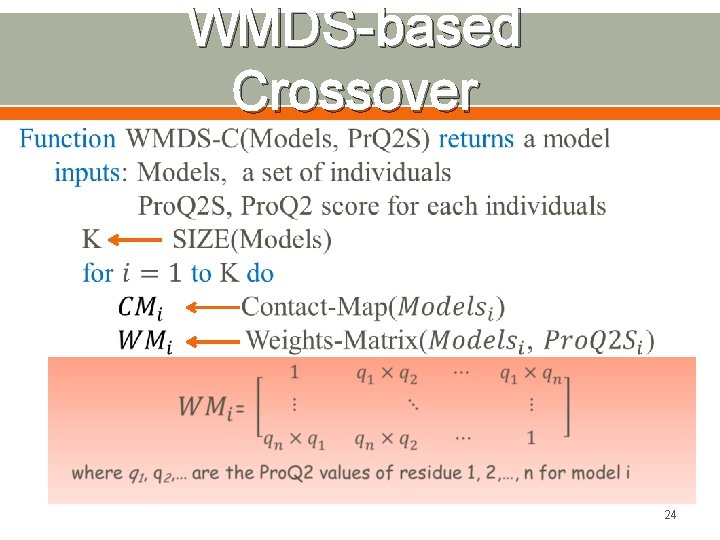
WMDS-based Crossover 24

Other Weights Matrix 25

MODELLER-based Crossover Function MODELLER-C(Models, Seq. F, Scripts. F) returns a model inputs: Models, a set of individuals Seq. F, Sequences file Script. F, Script file for MODELLER do run MODELLER(Models, Seq. F, Scripts. F) return the best model generate by MODELLER 26

Hybrid MDS and MODELLER-based Crossover 27

Example: P-2 P-WMDSMODELLER 28

Outline Existing Work q Foundations q Proposed Methods q Experimental Results q v Data Set v Computation time v Results using Pro. Q 2 as QA v Results using CGDT-TS as QA q Conclusions 29

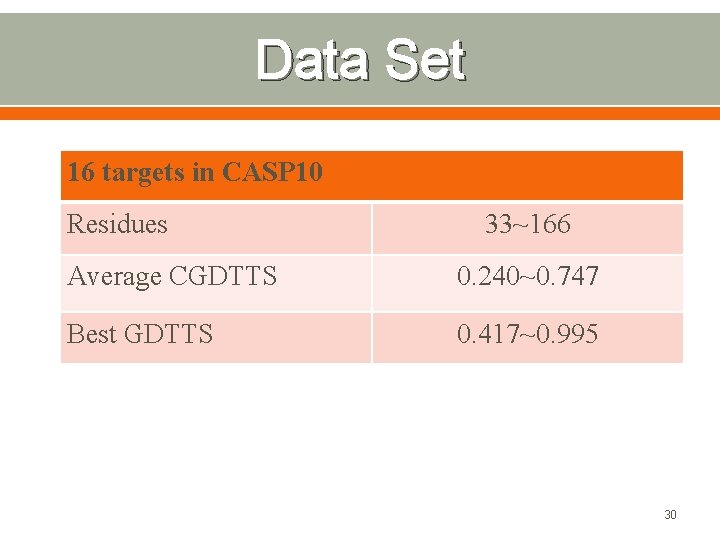
Data Set 16 targets in CASP 10 Residues 33~166 Average CGDTTS 0. 240~0. 747 Best GDTTS 0. 417~0. 995 30

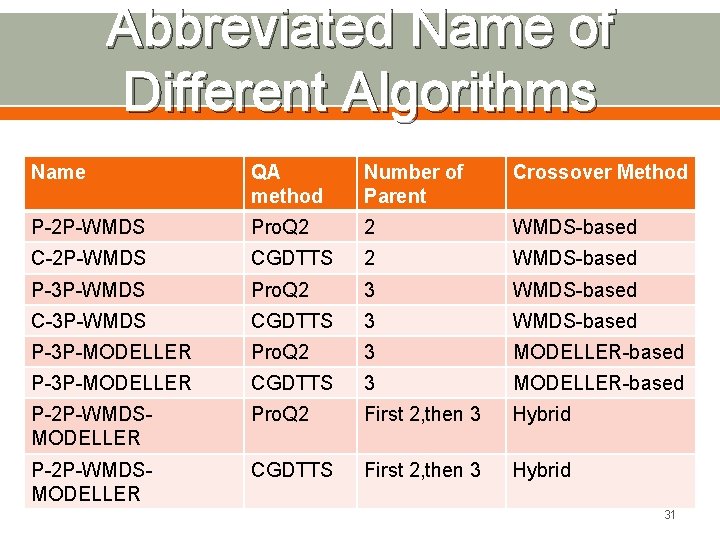
Abbreviated Name of Different Algorithms Name QA method Number of Parent Crossover Method P-2 P-WMDS Pro. Q 2 2 WMDS-based C-2 P-WMDS CGDTTS 2 WMDS-based P-3 P-WMDS Pro. Q 2 3 WMDS-based C-3 P-WMDS CGDTTS 3 WMDS-based P-3 P-MODELLER Pro. Q 2 3 MODELLER-based P-3 P-MODELLER CGDTTS 3 MODELLER-based P-2 P-WMDSMODELLER Pro. Q 2 First 2, then 3 Hybrid P-2 P-WMDSMODELLER CGDTTS First 2, then 3 Hybrid 31

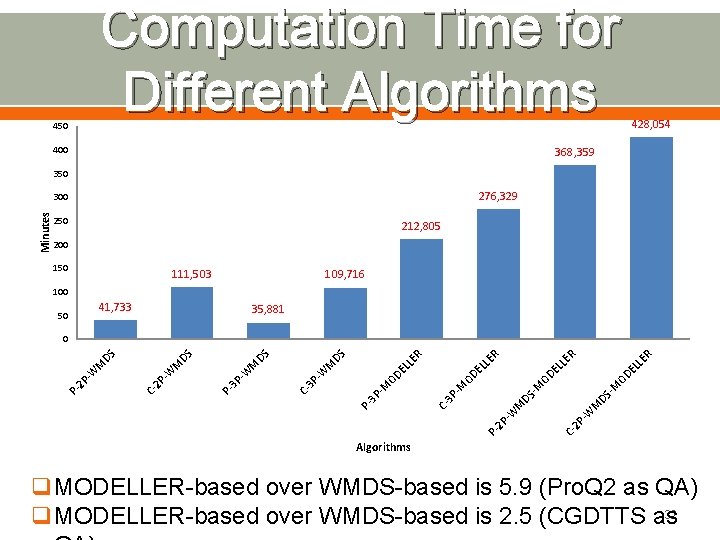
Computation Time for Different Algorithms 450 400 428, 054 368, 359 350 276, 329 Minutes 300 250 212, 805 200 150 111, 503 109, 716 100 41, 733 50 35, 881 R M DS - 2 P -W M C- P 2 P- W M C- 3 P DS -M -M OD OD EL LE LL ER LE R EL R OD EL LE -M P 3 P DS C- 3 P -W M DS 3 P -W M P- M -W 2 P C- P- 2 P -W M DS DS 0 Algorithms q. MODELLER-based over WMDS-based is 5. 9 (Pro. Q 2 as QA) 32 q. MODELLER-based over WMDS-based is 2. 5 (CGDTTS as

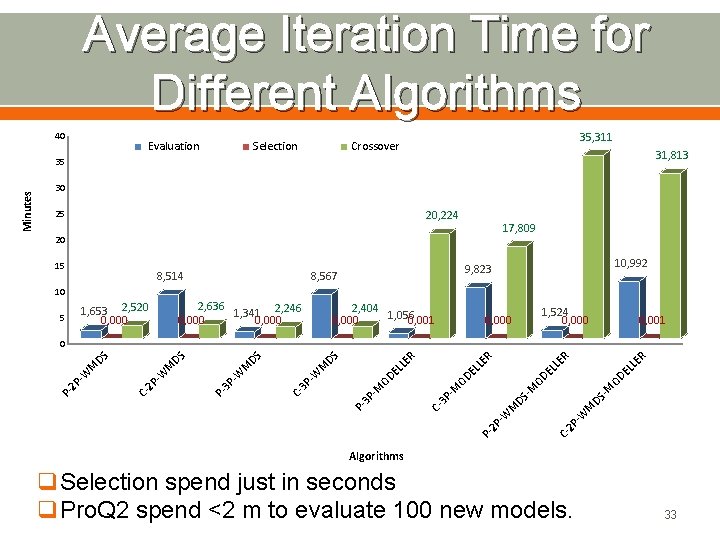
Average Iteration Time for Different Algorithms 40 Evaluation Selection 35, 311 Crossover 31, 813 30 20, 224 25 17, 809 20 15 8, 514 10, 992 9, 823 8, 567 10 2, 636 1, 341 2, 246 0, 000 1, 653 2, 520 0, 000 5 2, 404 1, 056 0, 000 0, 001 1, 524 0, 000 0, 001 R M -W 2 P C- P 2 P -W M DS DS - -M M OD OD E LL EL LE ER R EL LE OD -M 3 P C- P 3 P -M OD E LL ER DS C- 3 P -W M DS P- 3 P -W M M -W 2 P C- 2 P -W M DS DS 0 P- Minutes 35 Algorithms q. Selection spend just in seconds q. Pro. Q 2 spend <2 m to evaluate 100 new models. 33

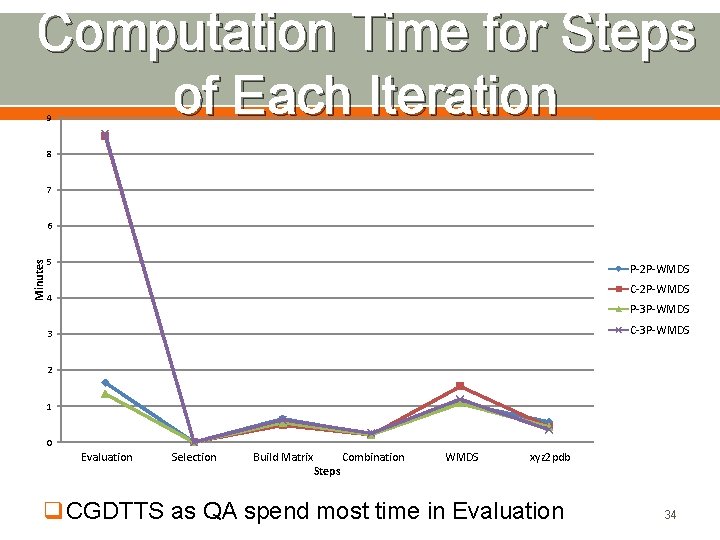
Computation Time for Steps of Each Iteration 9 8 7 Minutes 6 5 P-2 P-WMDS C-2 P-WMDS 4 P-3 P-WMDS C-3 P-WMDS 3 2 1 0 Evaluation Selection Build Matrix Steps Combination WMDS xyz 2 pdb q. CGDTTS as QA spend most time in Evaluation 34

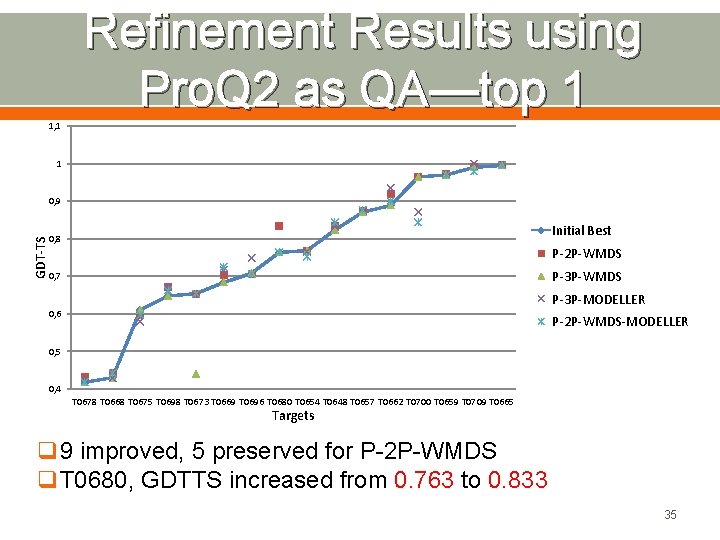
Refinement Results using Pro. Q 2 as QA—top 1 1, 1 1 GDT-TS 0, 9 Initial Best 0, 8 P-2 P-WMDS P-3 P-WMDS 0, 7 P-3 P-MODELLER 0, 6 P-2 P-WMDS-MODELLER 0, 5 0, 4 T 0678 T 0668 T 0675 T 0698 T 0673 T 0669 T 0696 T 0680 T 0654 T 0648 T 0657 T 0662 T 0700 T 0659 T 0709 T 0665 Targets q 9 improved, 5 preserved for P-2 P-WMDS q. T 0680, GDTTS increased from 0. 763 to 0. 833 35

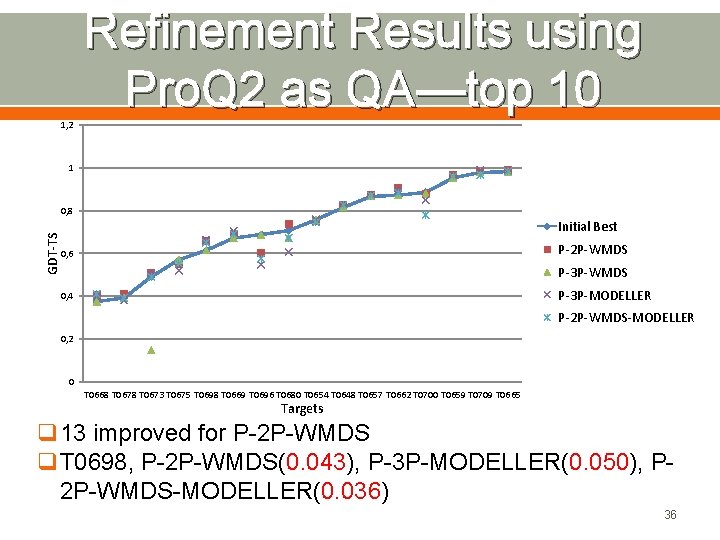
Refinement Results using Pro. Q 2 as QA—top 10 1, 2 1 GDT-TS 0, 8 Initial Best P-2 P-WMDS 0, 6 P-3 P-WMDS P-3 P-MODELLER 0, 4 P-2 P-WMDS-MODELLER 0, 2 0 T 0668 T 0673 T 0675 T 0698 T 0669 T 0696 T 0680 T 0654 T 0648 T 0657 T 0662 T 0700 T 0659 T 0709 T 0665 Targets q 13 improved for P-2 P-WMDS q. T 0698, P-2 P-WMDS(0. 043), P-3 P-MODELLER(0. 050), P 2 P-WMDS-MODELLER(0. 036) 36

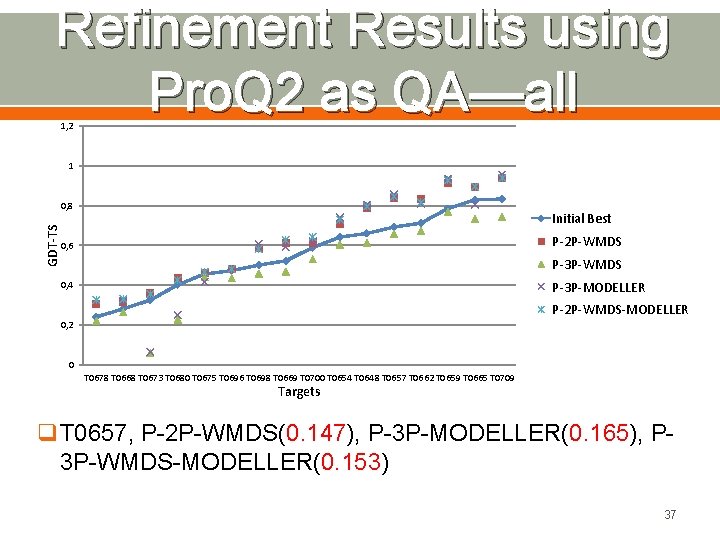
Refinement Results using Pro. Q 2 as QA—all 1, 2 1 GDT-TS 0, 8 Initial Best P-2 P-WMDS 0, 6 P-3 P-WMDS P-3 P-MODELLER 0, 4 P-2 P-WMDS-MODELLER 0, 2 0 T 0678 T 0668 T 0673 T 0680 T 0675 T 0696 T 0698 T 0669 T 0700 T 0654 T 0648 T 0657 T 0662 T 0659 T 0665 T 0709 Targets q. T 0657, P-2 P-WMDS(0. 147), P-3 P-MODELLER(0. 165), P 3 P-WMDS-MODELLER(0. 153) 37

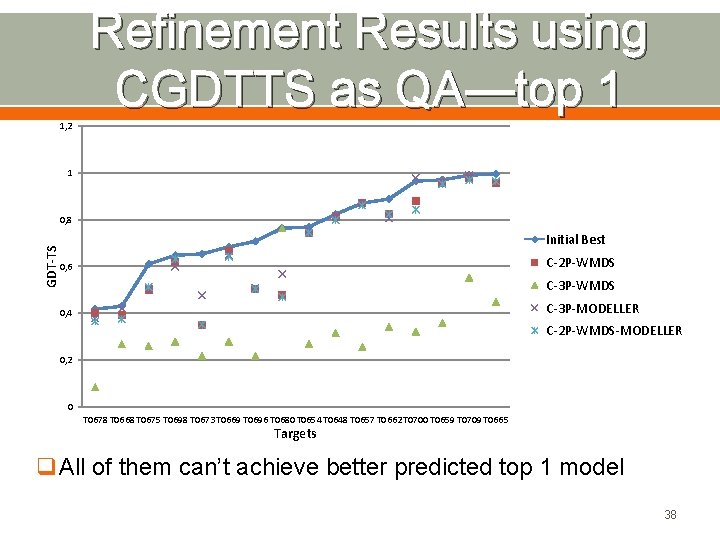
Refinement Results using CGDTTS as QA—top 1 1, 2 1 GDT-TS 0, 8 Initial Best C-2 P-WMDS 0, 6 C-3 P-WMDS C-3 P-MODELLER 0, 4 C-2 P-WMDS-MODELLER 0, 2 0 T 0678 T 0668 T 0675 T 0698 T 0673 T 0669 T 0696 T 0680 T 0654 T 0648 T 0657 T 0662 T 0700 T 0659 T 0709 T 0665 Targets q. All of them can’t achieve better predicted top 1 model 38

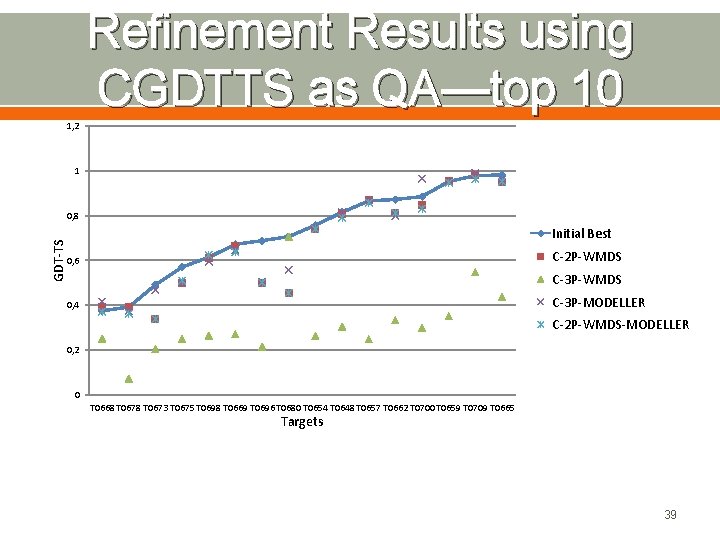
Refinement Results using CGDTTS as QA—top 10 1, 2 1 GDT-TS 0, 8 Initial Best C-2 P-WMDS 0, 6 C-3 P-WMDS C-3 P-MODELLER 0, 4 C-2 P-WMDS-MODELLER 0, 2 0 T 0668 T 0673 T 0675 T 0698 T 0669 T 0696 T 0680 T 0654 T 0648 T 0657 T 0662 T 0700 T 0659 T 0709 T 0665 Targets 39

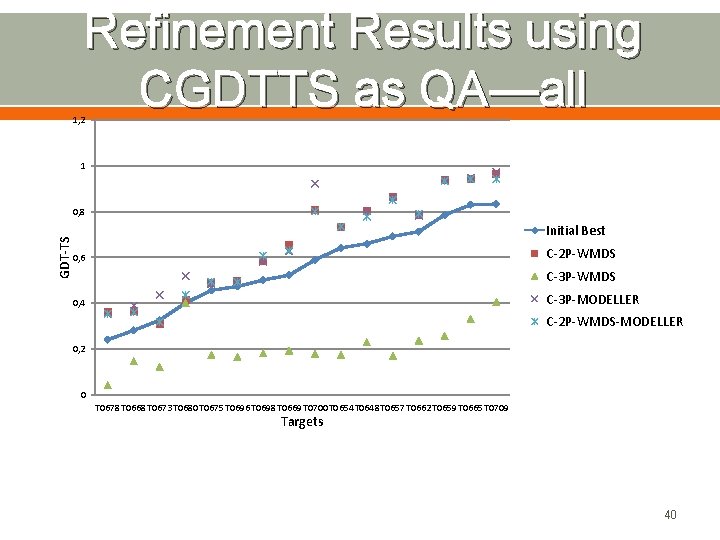
Refinement Results using CGDTTS as QA—all 1, 2 1 GDT-TS 0, 8 Initial Best C-2 P-WMDS 0, 6 C-3 P-WMDS C-3 P-MODELLER 0, 4 C-2 P-WMDS-MODELLER 0, 2 0 T 0678 T 0668 T 0673 T 0680 T 0675 T 0696 T 0698 T 0669 T 0700 T 0654 T 0648 T 0657 T 0662 T 0659 T 0665 T 0709 Targets 40

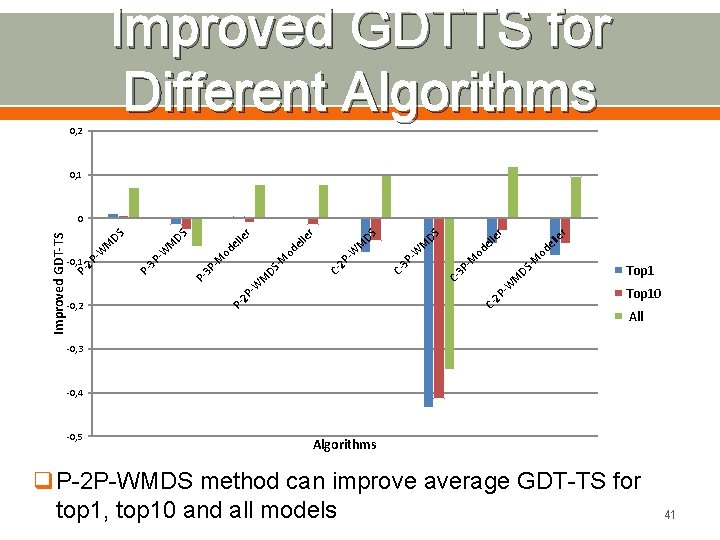
Improved GDTTS for Different Algorithms 0, 2 0, 1 C- 2 P r 2 P -W M C 3 P DS -M -M od e lle r DS C- 3 P -W M DS M -W -W M C- 2 P od el le r DS -M 3 P P- -0, 2 -M od el le r DS M P- -0, 1 P 3 P -W DS M P 2 P -W Improved GDT-TS 0 Top 10 All -0, 3 -0, 4 -0, 5 Algorithms q. P-2 P-WMDS method can improve average GDT-TS for top 1, top 10 and all models 41

Summary of the Experimental Results q The computation time for MODELLER-based over WMDS-based is 5. 9 using Pro. Q 2 as QA, CGDTTS as QA the ratio is 2. 5 q q P-2 P-WMDS EA improved GDT-TS of 9 models and 5 preserved out of 16 models for top 1 model; The true GDT-TS of best model for T 0680 is changed from 0. 763 to 0. 833 by using P-2 PWMDS method; 42

Summary of the Experimental Results q q 3 parents for WMDS-based EAs is failed in most cases; Using CGDT-TS as QA method can’t achieve better top 1 model and top 10 models. 43

Outline Existing Work q Foundations q Proposed Methods q Experimental Results q Conclusions q 44

Conclusions q This project applied EA framework and tested three algorithms: v WMDS-based method v MODELLER-based method v Hybrid method q WMDS-based method: v 3 parents v CGDTTS as QA v 2 parents, Pro. Q 2 as QA 45

Conclusions q MODELLER-based method: v The average computation time for each target is more than 3. 5 hours; v could achieve better models in some cases; q Hybrid method: v could attain few better models sometimes; v Can’t improve the average GDTTS for each target on top 1 and top 10 46

Conclusions q Compare three EAs v The computation time for MODELLER-based method are slow than WMDS-based method; v Pro. Q 2 evaluation method fast than CGDTTS; v Except 3 parents, all methods could improve the overall quality of the population; v Only P-2 P-WMDS could improve the average GDTTS of each target on top 1, top 10 and all models. 47

Future Works q q Multi-parents for WMDS-based refinement needs more research; Known the best starting model, then refine it. 48

Acknowledgements Prof. Shang, Prof. Xu, Prof. Kosztin q All group members and friends q Husband Relatives q 49