Multidimensional Scaling Agenda Multidimensional Scaling Goodness of fit

Multidimensional Scaling

Agenda • Multidimensional Scaling • Goodness of fit measures • Nosofsky, 1986

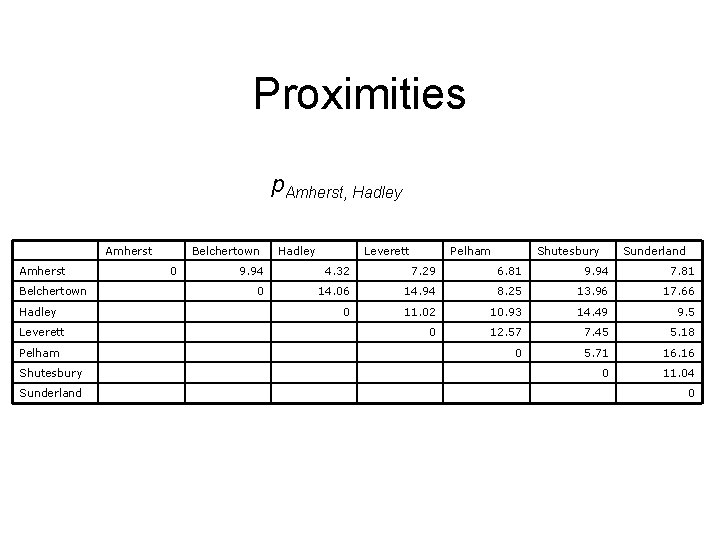
Proximities p. Amherst, Hadley Amherst Belchertown Hadley Leverett Pelham Shutesbury Sunderland Belchertown 0 Hadley Leverett Pelham Shutesbury Sunderland 9. 94 4. 32 7. 29 6. 81 9. 94 7. 81 0 14. 06 14. 94 8. 25 13. 96 17. 66 0 11. 02 10. 93 14. 49 9. 5 0 12. 57 7. 45 5. 18 0 5. 71 16. 16 0 11. 04 0

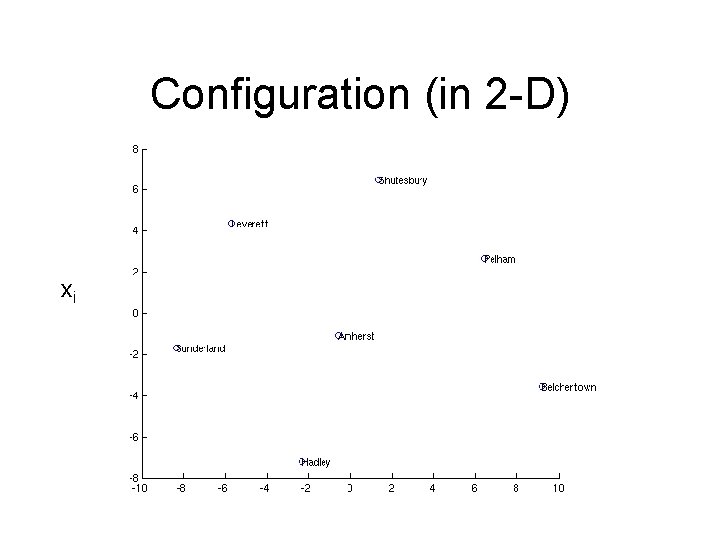
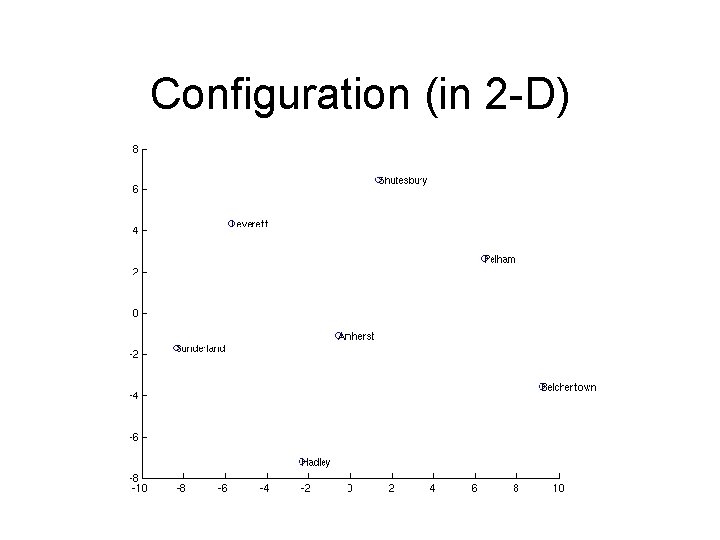
Configuration (in 2 -D) xi

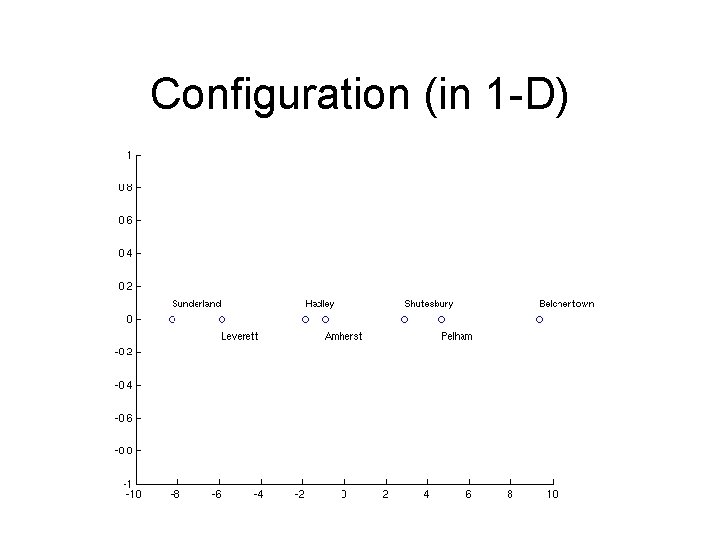
Configuration (in 1 -D)

Formal MDS Definition • f: pij dij(X) • MDS is a mapping from proximities to corresponding distances in MDS space. • After a transformation f, the proximities are equal to distances in X. Amherst Belcherto wn Hadley Leverett Pelham Shutesbu ry Sunderla nd 0 Belcherto wn Hadley Leverett Pelham Shutesbu ry Sunderla nd 9. 94 4. 32 7. 29 6. 81 9. 94 7. 81 0 14. 06 14. 94 8. 25 13. 96 17. 66 0 11. 02 10. 93 14. 49 9. 5 0 12. 57 7. 45 5. 18 0 5. 71 16. 16 0 11. 04 0

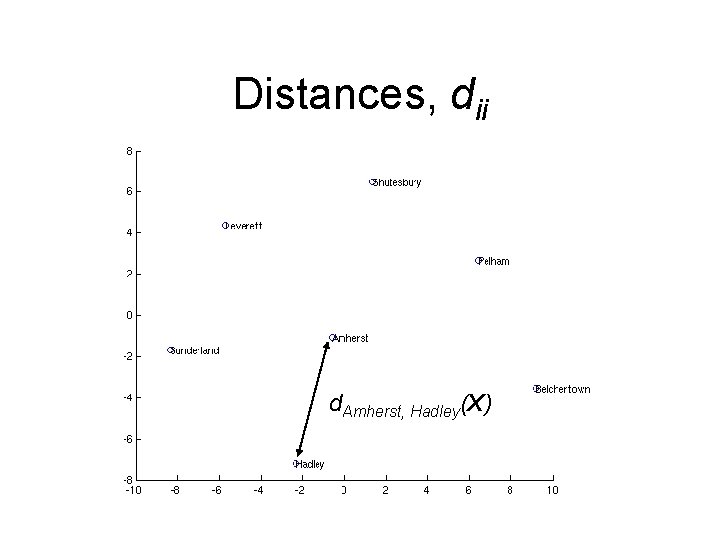
Distances, dij d. Amherst, Hadley(X)

Distances, dij

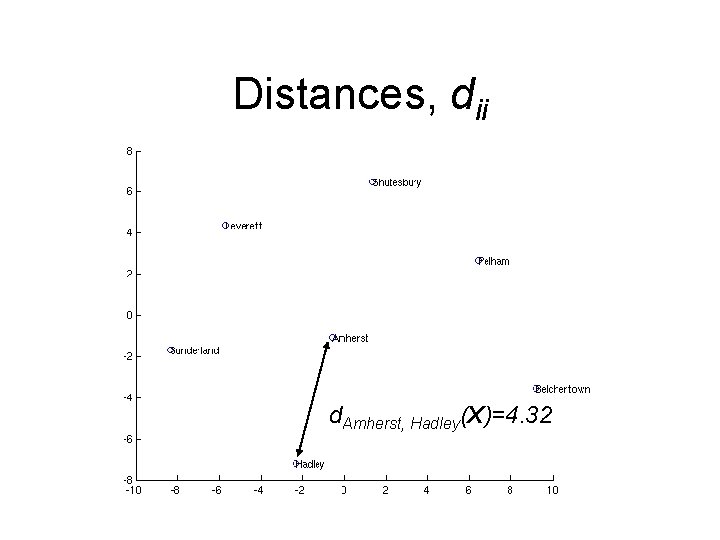
Distances, dij d. Amherst, Hadley(X)=4. 32

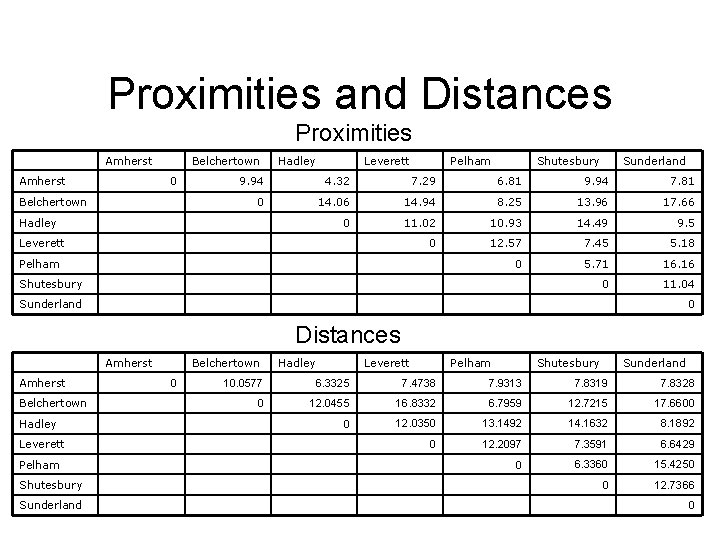
Proximities and Distances Proximities Amherst Belchertown 0 Belchertown Hadley Leverett Pelham Shutesbury Sunderland 9. 94 4. 32 7. 29 6. 81 9. 94 7. 81 0 14. 06 14. 94 8. 25 13. 96 17. 66 0 11. 02 10. 93 14. 49 9. 5 0 12. 57 7. 45 5. 18 0 5. 71 16. 16 0 11. 04 Hadley Leverett Pelham Shutesbury Sunderland 0 Distances Amherst Belchertown Hadley Leverett Pelham Shutesbury Sunderland Belchertown 0 Hadley Leverett Pelham Shutesbury Sunderland 10. 0577 6. 3325 7. 4738 7. 9313 7. 8319 7. 8328 0 12. 0455 16. 8332 6. 7959 12. 7215 17. 6600 0 12. 0350 13. 1492 14. 1632 8. 1892 0 12. 2097 7. 3591 6. 6429 0 6. 3360 15. 4250 0 12. 7366 0

The Role of f • f relates the proximities to the distances. • f(pij)=dij(X)

The Role of f • f can be linear, exponential, etc. • In psychological data, f is usually assumed any monotonic function. – That is, if pij<pkl then dij(X) dkl(X). – Most psychological data is on an ordinal scale, e. g. , rating scales.

Looking at Ordinal Relations Proximities Amherst Belchertown 0 Belchertown Hadley Leverett Pelham Shutesbury Sunderland 9. 94 4. 32 7. 29 6. 81 9. 94 7. 81 0 14. 06 14. 94 8. 25 13. 96 17. 66 0 11. 02 10. 93 14. 49 9. 5 0 12. 57 7. 45 5. 18 0 5. 71 16. 16 0 11. 04 Hadley Leverett Pelham Shutesbury Sunderland 0 Distances Amherst Belchertown Hadley Leverett Pelham Shutesbury Sunderland Belchertown 0 Hadley Leverett Pelham Shutesbury Sunderland 10. 0577 6. 3325 7. 4738 7. 9313 7. 8319 7. 8328 0 12. 0455 16. 8332 6. 7959 12. 7215 17. 6600 0 12. 0350 13. 1492 14. 1632 8. 1892 0 12. 2097 7. 3591 6. 6429 0 6. 3360 15. 4250 0 12. 7366 0

Stress • It is not always possible to perfectly satisfy this mapping. • Stress is a measure of how closely the model came. • Stress is essentially the scaled sum of squared error between f(pij) and dij(X)

Stress “Correct” Dimensionality Dimensions

Distance Invariant Transformations • Scaling (All X doubled in size (or flipped)) • Rotatation (X rotated 20 degrees left) • Translation (X moved 2 to the right)

Configuration (in 2 -D)

Rotated Configuration (in 2 -D)

Uses of MDS • Visually look for structure in data. • Discover the dimensions that underlie data. • Psychological model that explains similarity judgments in terms of distance in MDS space.

Simple Goodness of Fit Measures • Sum-of-squared error (SSE) • Chi-Square • Proportion of variance accounted for (PVAF) • R 2 • Maximum likelihood (ML)

Sum of Squared Error Data Prediction (Data-Prediction)2 7 5. 03 3. 88 8 6. 97 1. 06 1 2. 12 1. 25 8 8. 91 0. 83 6 6. 97 0. 94 SSE 7. 97

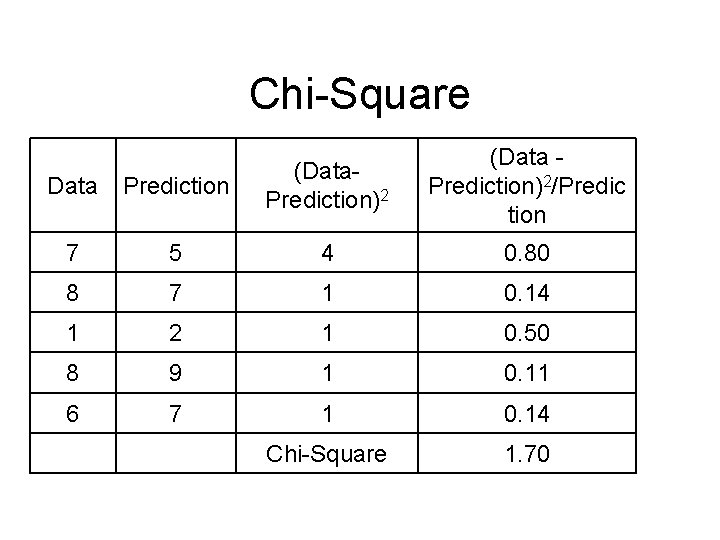
Chi-Square (Data Prediction)2/Predic tion Data Prediction (Data. Prediction)2 7 5 4 0. 80 8 7 1 0. 14 1 2 1 0. 50 8 9 1 0. 11 6 7 1 0. 14 Chi-Square 1. 70

Proportion of Variance Accounted for Data 7 8 1 8 6 Mean Prediction Mean Error 2 6 1 1 6 2 4 6 6 6 -5 2 0 SST 25 4 0 34 Model Prediction Error 2 5. 03 1. 97 3. 88 6. 97 1. 03 1. 06 2. 12 8. 91 6. 97 -1. 12 -0. 91 -0. 97 SSE (SST-SSE)/SST = (34 -7. 96)/34 =. 77 1. 25 0. 83 0. 94 7. 96

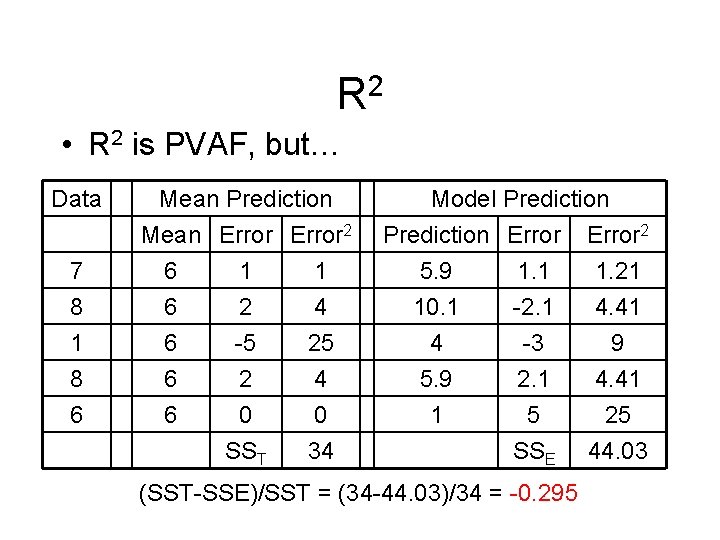
R 2 • R 2 is PVAF, but… Data 7 8 1 8 6 Mean Prediction Mean Error 2 6 1 1 6 2 4 6 6 6 -5 2 0 SST 25 4 0 34 Model Prediction Error 2 5. 9 1. 1 1. 21 10. 1 -2. 1 4. 41 4 5. 9 1 -3 2. 1 5 SSE (SST-SSE)/SST = (34 -44. 03)/34 = -0. 295 9 4. 41 25 44. 03

Maximum Likelihood • Assume we are sampling from a population with probability f(Y; ). • The Y is an observation and the are the model parameters. =[0] Y N(-1. 7; [ =0])=0. 094

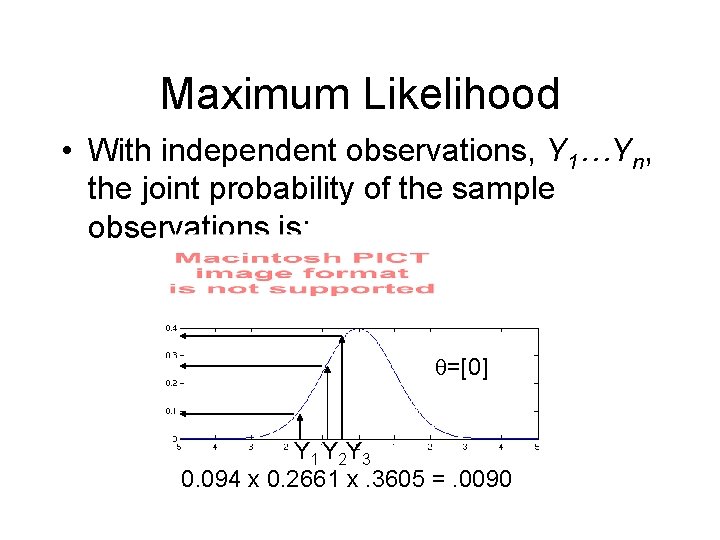
Maximum Likelihood • With independent observations, Y 1…Yn, the joint probability of the sample observations is: =[0] Y 1 Y 2 Y 3 0. 094 x 0. 2661 x. 3605 =. 0090

Maximum Likelihood • Expressed as a function of the parameters, we have the likelihood function: • The goal is to maximize L with respect to the parameters, .

Maximum Likelihood =[0] Y 1 Y 2 Y 3 0. 094 x 0. 2661 x. 3605 =. 0090 =[-1. 0167] Y 1 Y 2 Y 3 0. 3159 x 0. 3962 x. 3398 =. 0425 (Assuming =1)

Maximum Likelihood • Preferred to other methods – Has very nice mathematical properties. – Easier to interpret. – We’ll see specifics in a few weeks. • Often harder (or impossible? ) to calculate than other methods. • Often presented as log likelihood, ln(ML). – Easier to compute (sums, not products). – Better numerical resolution. • Sometimes equivalent to other methods. – E. g. , same as SSE when calculating mean of a distribution.