Multidimensional Arrays 01204111 Computer and Programming Agenda Quick

Multidimensional Arrays 01204111 Computer and Programming

Agenda • Quick review on 1 -dimensional array. • Declaring and creating multidimensional arrays • 2 -dimensional array – Nested for-loop – Applications • 3 -dimensional array

Quick review

Quick review (1) • What is the output of the following program? int [] a = new int[5]; for(int i=0; i<5; i++) a[i] = 10 - i; for(int i=0; i<5; i++) Console. Write. Line(a[i]); 10 9 8 7 6

Quick review (2) • What is the output of the following program? int [] a = new int[5]; for(int i=0; i<5; i++) a[i] = 10 – i*2; for(int i=1; i<=5; i++) Console. Write. Line(a[i]); You are trying to access a[5] which does not exist. You will see an error message: System. Index. Out. Of. Range. Exception. 10 8 6 4 2

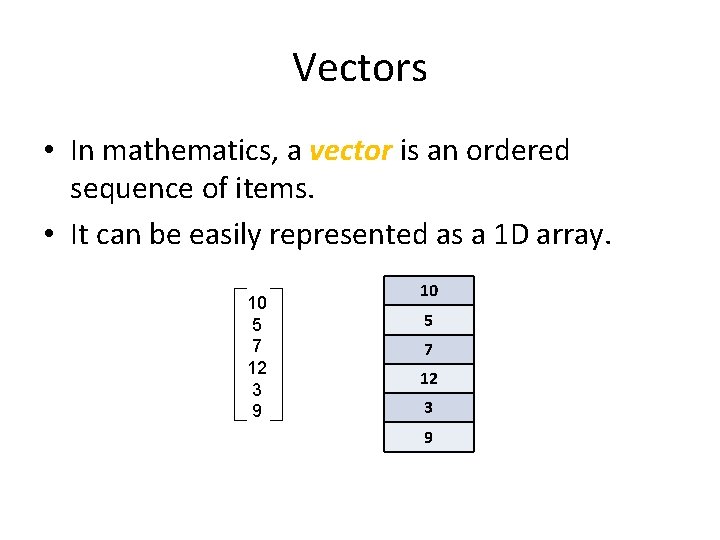
Vectors • In mathematics, a vector is an ordered sequence of items. • It can be easily represented as a 1 D array. 10 5 7 12 3 9

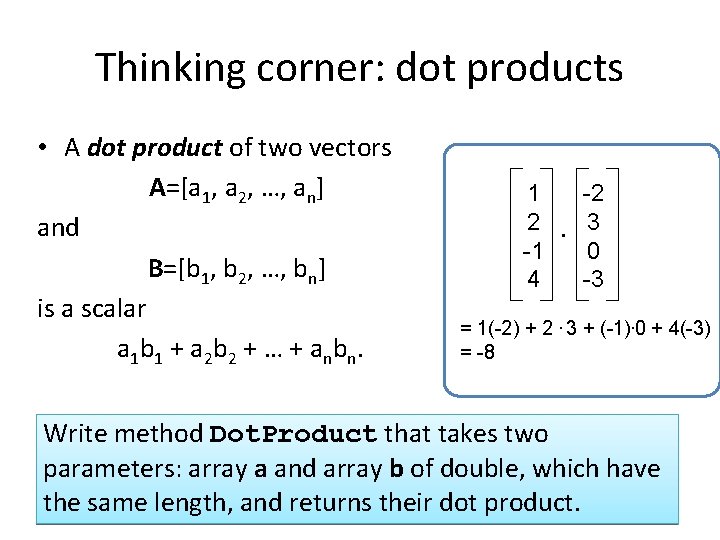
Thinking corner: dot products • A dot product of two vectors A=[a 1, a 2, …, an] and B=[b 1, b 2, …, bn] is a scalar a 1 b 1 + a 2 b 2 + … + a n b n. 1 2 -1 4 . -2 3 0 -3 = 1(-2) + 2. 3 + (-1). 0 + 4(-3) = -8 Write method Dot. Product that takes two parameters: array a and array b of double, which have the same length, and returns their dot product.

Dot product: solution static double Dot. Product(double [] a, double [] b) { int d = a. Length; double p = 0; (Click to show) for(int i = 0; i < d; i++) p += a[i] * b[i]; return p; }

2 -dimensional arrays

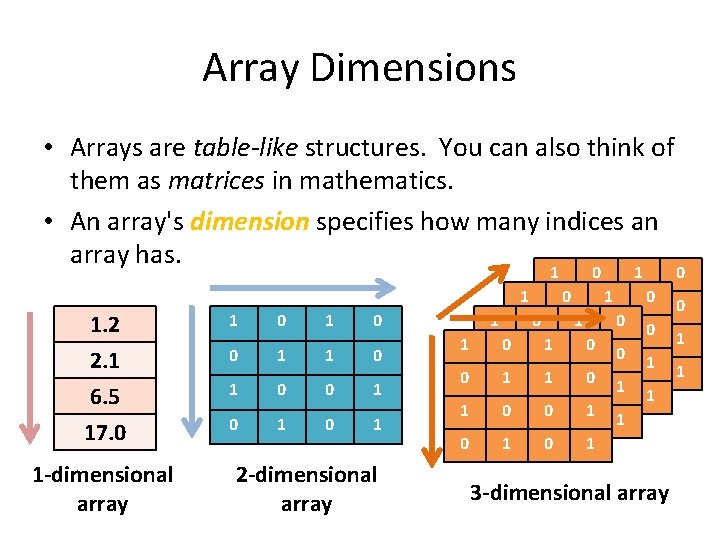
Array Dimensions • Arrays are table-like structures. You can also think of them as matrices in mathematics. • An array's dimension specifies how many indices an array has. 1 0 1 1 1. 2 2. 1 6. 5 17. 0 1 -dimensional array 1 0 0 1 1 1 0 0 1 0 1 2 -dimensional array 1 1 0 00 11 10 00 111 010 00 1 10 0 1 1 00 10 01 1 00 1 0 1 10 01 1 0 1 3 -dimensional array 0 0 1 1

Higher Dimensions • You can arrays with higher than 3 dimensions, but it will be very hard to visualize. • In this course, we shall not focus on them. 1 1 1 0 0 1 1 0 0 1 1 00 0 1 1 0 0 0 1 0 0 1 1 0 0 1 1 1 1 0 0 1 1 0 0 1 1 00 0 1 1 0 0 0 1 1 1 0 0 1 1 0 0 1 1 0 0 1 1 00 0 1 1 0 0 0 1 1 2 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 00 0 1 1 0 0 0 1 1 3 0 1 1 0 0 1 1 1 0 0 1

1 D, 2 D, 3 D, … • To save space, we sometimes refer to – 1 -dimensional arrays as 1 D arrays – 2 -dimensional arrays as 2 D arrays – 3 -dimensional arrays as 3 D arrays 1 D 2 D 3 D

2 -dimensional arrays: declaration • Since 2 -dimensional arrays have 2 indices, when we declare them, we put 1 comma in the brackets: type [, ] varname;

2 -dimensional arrays: creation • To create the array, we use the new operator and supply the ranges of both indices. int [, ] tab; tab = new int[3, 4]; tab 0 0 0

Elements in an array int [, ] tab; tab = new int[3, 4]; tab 0 1 2 Both indices run from 0 to their range minus one. 0 1 2 3 tab[0, 0] tab[1, 0] tab[2, 0] tab[0, 1] tab[1, 1] tab[2, 1] tab[0, 2] tab[1, 2] tab[2, 2] tab[0, 3] tab[1, 3] tab[2, 3]

Example 1 int [, ] d; d = new int[2, 2]; d[0, 0] = 7; d[0, 1] = 9; d[1, 0] = 3; d[1, 1] = 6; d 7 0 0 3 9 0 0 6 Do not forget that an array must be created with the new operator before using it.

Array initialization • As in 1 D arrays, we can initialize a 2 D array when we create it. int [, ] a = new int [2, 3] { { 10, 1000 }, {20, 2000 } }; 10 20 100 200 • We can also leave the new part out. int [, ] a = new int [2, 3] { { 10, 1000 }, {20, 2000 } }; int [, ] a = { { 10, 1000 }, {20, 2000 } }; 1000 2000

How to visualize a 2 D array (1) • You can view it in either direction. double [, ] a = new double[5, 3]; a[0, 0] a[0, 1] a[0, 0] a[1, 1] a[1, 2] a[2, 0] a[2, 1] a[2, 2] a[3, 0] a[3, 1] a[3, 2] a[4, 0] a[4, 1] a[4, 2] a[0, 0] a[1, 0] a[2, 0] a[3, 0] a[4, 0] a[0, 1] a[1, 1] a[2, 1] a[3, 1] a[4, 1] a[0, 2] a[1, 2] a[2, 2] a[3, 2] a[4, 2] It usually does not matter which way you visualize it, as long as the first index runs from 0 to 4, and the second index runs from 0 to 2.

How to visualize a 2 D array (2) • However, in C# the way you initialize a 2 D array is to group the elements based on the first index first. double [, ] a = { {1, 2, 3}, {4, 5, 6}, {7, 8, 9}, {10, 11, 12}, {13, 14, 15} }; a[0, 0] 1 a[0, 1] 2 a[0, 0] 3 a[1, 0] 4 a[1, 1] 5 a[1, 2] 6 a[2, 0] 7 a[2, 1] 8 a[2, 2] 9 a[3, 0] 10 a[3, 1] 11 a[3, 2] 12 a[4, 0] 13 a[4, 1] 14 a[4, 2] 15 This is also how the array is stored in the memory.

Example 2 (1) • You can use a 2 D array to represent many table-like data. int [, ] map = { {1, 0, 1, 1, 1, 0, 1}, {1, 0, 0, 0}, {1, 1, 1, 0}, {1, 1, 0, 0}, {0, 0, 0, 1, 1, 0, 1}, {1, 0, 1, 1, 1, 0, 1} }; It's a maze!

Example 2 (2) • How to display the maze on the screen? Console. Write. Line("{0}{1}{2}{3}{4}{5}{6}", map[0, 0], map[0, 1], map[0, 2], map[0, 3], map[0, 4], map[0, 5], map[0, 6]); Console. Write. Line("{0}{1}{2}{3}{4}{5}{6}", map[1, 0], map[1, 1], map[1, 2], map[1, 3], map[1, 4], map[1, 5], map[1, 6]); //… and so on This is a bad idea. int [, ] map = { {1, 0, 1, 1, 1, 0, 1}, {1, 0, 0, 0}, {1, 1, 1, 0}, {1, 1, 0, 0}, {0, 0, 0, 1, 1, 0, 1}, {1, 0, 1, 1, 1, 0, 1} };

Example 2 (3) • Let's try to print just the first line first! Console. Write. Line("{0}{1}{2}{3}{4}{5}{6}", map[0, 0], map[0, 1], map[0, 2], map[0, 3], map[0, 4], map[0, 5], map[0, 6]); How can we remove these duplications? Use some kind of loops! for(int i = 0; i < 7; i++) Console. Write("{0}", map[0, i]); Console. Write. Line();

Thinking corner • Can you write a program that prints the whole map (in 0 and 1)? // This only prints the first line for(int i = 0; i < 7; i++) Console. Write("{0}", map[0, i]); Console. Write. Line(); This index specify which line to be printed.

Thinking corner: solution • We can loop over the first index as well. for(int j = 0; j < 6; j++) { // This prints one line for(int i = 0; i < 7; i++) (Click to show) Console. Write("{0}", map[j, i]); Console. Write. Line(); }

Thinking corner: a nicer solution • We can have a better maze by printing # and. instead of 1 and 0. for(int j = 0; j < 6; j++) { // This prints one line for(int i = 0; i < 7; i++) if(map[j, i]==0) Console. Write(". "); else Console. Write("#"); Console. Write. Line(); } #. ###. # 1011101 1000000 #. . . 1110110 ###. (Click to show) 1100100 ##. . 0001101. . . ##. # 1011101 #. ###. #

Array lengths • The program in the previous example does not work right away when we change the size of the maze, because we put 6 and 7 in the code. for(int j = 0; j < 6; j++) { // … for(int i = 0; i < 7; i++) // … Console. Write. Line(); } However, we can read these length directly from the array.

Array properties / methods • Method Get. Length( j ) – returns the length of the j-th index; the first index starts at 0. • Property Length – returns the total number of elements double [, ] temp = new double[10, 30]; Console. Write. Line(temp. Get. Length(0)); Console. Write. Line(temp. Get. Length(1)); Console. Write. Line(temp. Length); 10 30 300

Thinking corner: final solution • We read the lengths from the array itself. So that our code works when we change array initialization. for(int j = 0; j < map. Get. Length(1); j++) { // … for(int i = 0; i < map. Get. Length(2); i++) // … Console. Write. Line(); }

Matrices: 2 D arrays

Matrices • We can naturally represent matrices as 2 D arrays. 1 3 0 0 7 9 1 0 5 5 4 0 Usually the matrix entries are floating-point number. So we usually declare an array of double for a matrix.

Quick Review • We have a 2 D array mat representing a matrix. • How can we know its "dimension"? I. e. , how many rows and how many columns does mat have? mat. Get. Length(1) mat. Get. Length(0) 1 3 0 0 7 9 1 0 5 5 4 0

Thinking Corner: how many zero's? • Write method Count. Zero that takes – A 2 D array mat and returns the number of zero entries in mat. static int Count. Zero(double [, ] mat) { takes a 2 D array int zcount = 0; for(int r = 0; r < mat. Get. Length(0); r++) for(int c = 0; c < mat. Get. Length(1); c++) (Click to show) if(mat[r, c] == 0) zcount++; return zcount; }

Nested for-loops • When working with 2 D arrays, we usually have to write nested loop to iterate over all elements in the arrays.

Quick practice (1) • What is the output of this program? for(int i=0; i<4; i++) for(int j=0; j<2; j++) Console. Write. Line("{0}, {1}", i, j); We often learn how nested loops work by considering from the inner loop. • This inner loop runs twice. • For the first round, j=0, and j=1 in the second round. • It prints whatever the value of variable i with the value of j. 0, 0 0, 1 1, 0 1, 1 2, 0 2, 1 3, 0 3, 1 i, 0 i, 1

Quick practice (2) • What is the output of this program? for(int i=0; i<4; i++) for(int j=0; j<=i; j++) Console. Write. Line("{0}, {1}", i, j); What can we learn by looking at the inner loop? • This inner loop may runs many times depending on the value of i. • It runs variable j from 0 to i. • It prints whatever the value of variable i with the value of j. 0, 0 1, 1 2, 0 2, 1 2, 2 3, 0 3, 1 3, 2 3, 3 i, 0 i, 1. . . i, i

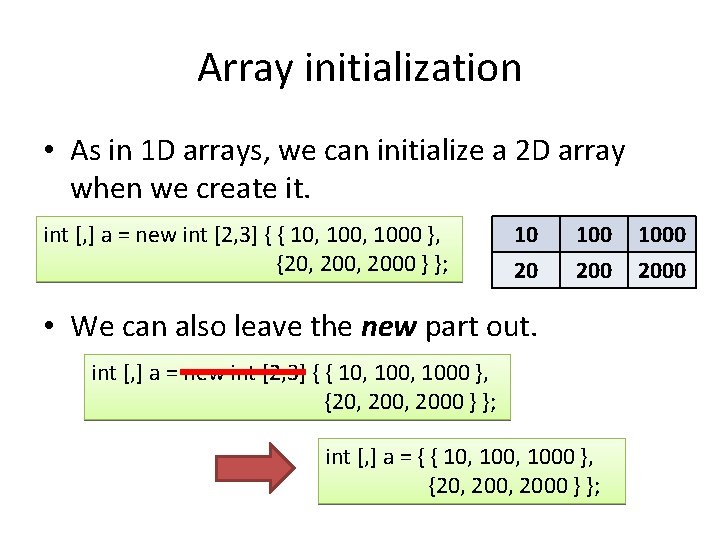
How to read matrices • Write a method Read. Matrix that takes as parameters: – integer r denoting the number of rows – integer c denoting the number of columns, reads a r x c matrix from the user, and returns the matrix. • The user will enter one double 1 0 1 per line, starting from the first row 3 7 0 in the following order: 0 9 5 5 4 0

Method Read. Matrix static double [, ] Read. Matrix(int r, int c) { double [, ] mat = new double[r, c]; Create the array. Read each entry for(int i = 0; i < r; i++) for(int j = 0; j < c; j++) mat[i, j] = double. Parse(Console. Read. Line()); Return the array } return mat;

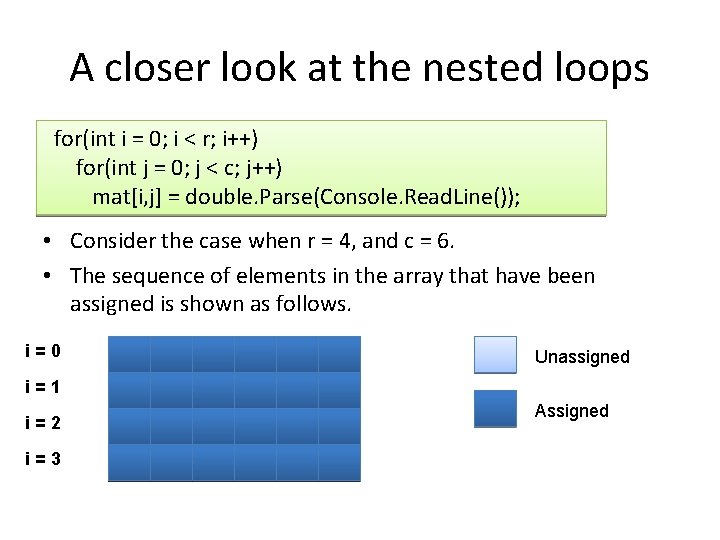
A closer look at the nested loops for(int i = 0; i < r; i++) for(int j = 0; j < c; j++) mat[i, j] = double. Parse(Console. Read. Line()); • Consider the case when r = 4, and c = 6. • The sequence of elements in the array that have been assigned is shown as follows. i=0 Unassigned i=1 i=2 i=3 Assigned

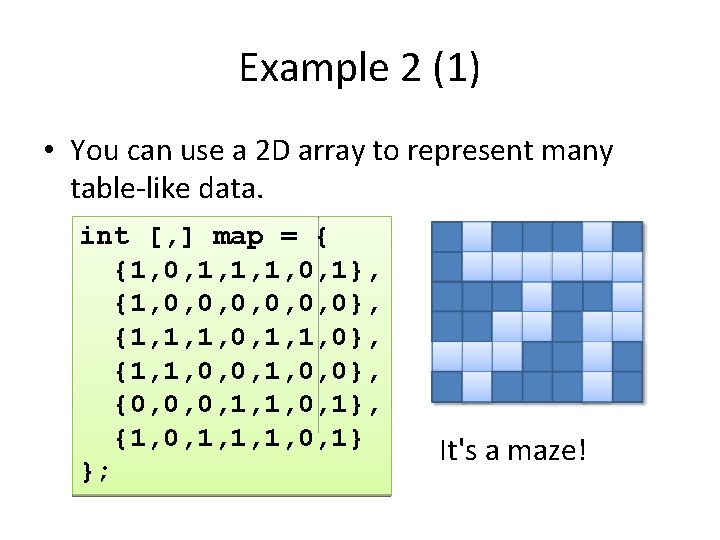
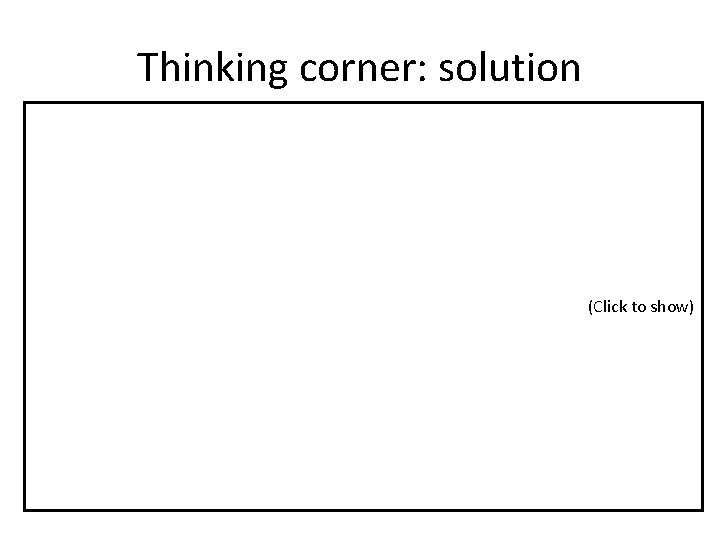
Thinking corner: matrix addition (1) • Write method Add. Matrix that takes matrices a and b and returns a new matrix c = a + b. • Note that you have to create matrix c inside method Add. Matrix. • What does the method look like? returns a 2 D array static double [, ] Add. Matrix(double [, ] a, double [, ] b) { }

Thinking corner: matrix addition (2) • To create 2 D array c, we have to read the matrix dimension from a and b. static double [, ] Add. Matrix(double [, ] a, double [, ] b) { double [, ] c = new double[a. Get. Length(0), a. Get. Length(1)]; // add a and b } return c;

Thinking corner: solution to matrix addition (3) static double [, ] Add. Matrix(double [, ] a, double [, ] b) { double [, ] c = new double[a. Get. Length(0), a. Get. Length(1)]; for(int r = 0; r < a. Get. Length(0); r++) for(int c = 0; c < a. Get. Length(1); c++) c[r, c] = a[r, c] + b[r, c]; } return c; (Click to show)

Upper right corner • Often we would like to find the sum of elements in a specific part of the matrix. • In this case, we are given 1 0 1 an n x n matrix and 3 7 0 we would like to find 0 9 5 the sum of the upper right 1 0 1 corner entries. 5 4 0 3

Quick analysis (1) • Let's start with a specific example. • Let n be 4. • These are the list of columns that you have to sum, for each row. – – row 1: 1, 2, 3, 4 row 2: 2, 3, 4 row 3: 3, 4 row 4: 4 1 3 0 1 0 7 9 0 1 0 5 1 • In general: in row i, you will have to look at column i, i + 1, i + 2, …, n. 5 4 0 3

Quick analysis (2): 0 -index • In general: in row i, you will have to look at column i, i + 1, i + 2, …, n. This is based on counting rows and columns starting at 1. • Don't forget the our indices start at 0. – Row numbers start at 0, end at n-1. – In row i, sum entries in columns i, i+1, …, n-1.

Solution static double Sum. Upper. Right(double [, ] mat) { int n = mat. Get. Length(0); double sum = 0; Work on row i for(int i = 0; i < n; i++) Work on entries. column j, in row i for(int = i; j < n; right j++) corner Sumj upper entries in row i. sum += Sum mat[i, j]; } return sum;

3 -dimensional arrays

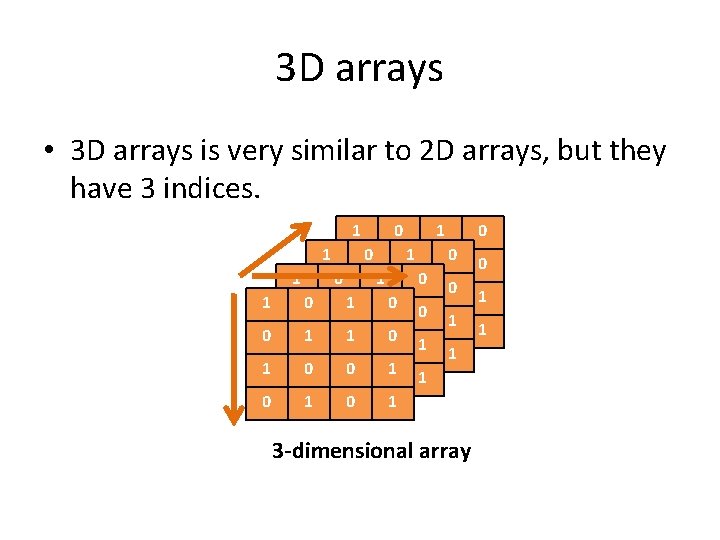
3 D arrays • 3 D arrays is very similar to 2 D arrays, but they have 3 indices. 1 0 1 1 00 0 11 1 00 1 0 00 11 10 00 111 010 00 1 10 0 1 1 00 10 01 1 00 1 0 1 10 01 1 0 1 3 -dimensional array 0 0 1 1

Declaration, creation, and initialization • Declaration: type [, , ] varname; int [, , ] credits; • Creation: varname = new type[s 1, s 2, s 3]; credits = new int[50, 4, 5]; • Initialization: int [, , ] credits = { {{ 1, 2 }, { 3, 4 }, {4, 5}}, {{ 6, 7 }, { 8, 9 }, {10, 11}} };

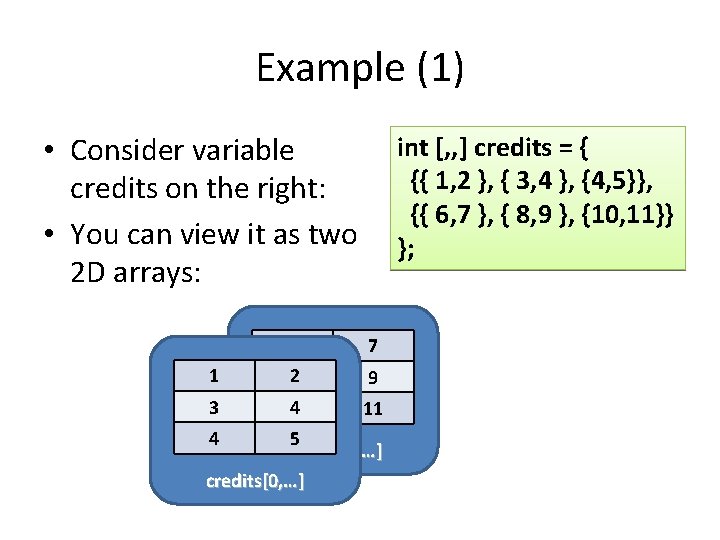
Example (1) • Consider variable credits on the right: • You can view it as two 2 D arrays: 1 3 6 82 int [, , ] credits = { {{ 1, 2 }, { 3, 4 }, {4, 5}}, {{ 6, 7 }, { 8, 9 }, {10, 11}} }; 7 9 4 10 11 4 5 credits[1, …] credits[0, …]

Example • Sample operations credits[0, 2, 1] = 100; credits[1, 1, 0] = 50; int [, , ] credits = { {{ 1, 2 }, { 3, 4 }, {4, 5}}, {{ 6, 7 }, { 8, 9 }, {10, 11}} }; 1 2 6 7 3 4 50 8 9 4 5 100 10 11 credits[0, …] credits[1, …]

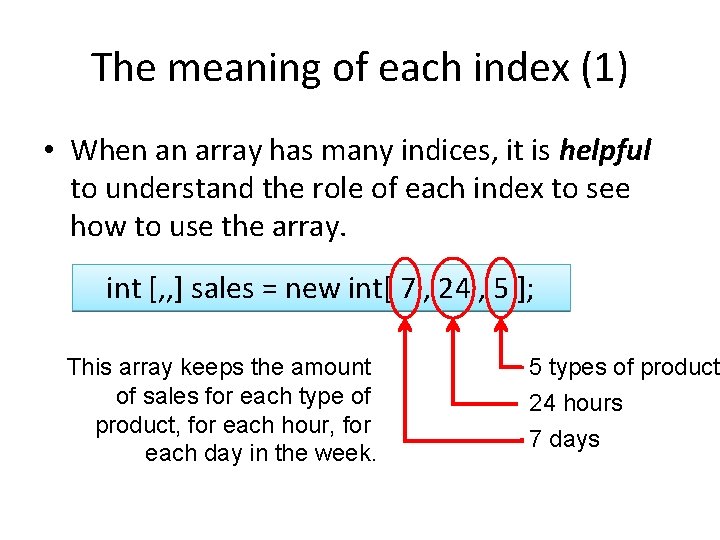
The meaning of each index (1) • When an array has many indices, it is helpful to understand the role of each index to see how to use the array. int [, , ] sales = new int[ 7 , 24 , 5 ]; This array keeps the amount of sales for each type of product, for each hour, for each day in the week. 5 types of product 24 hours 7 days

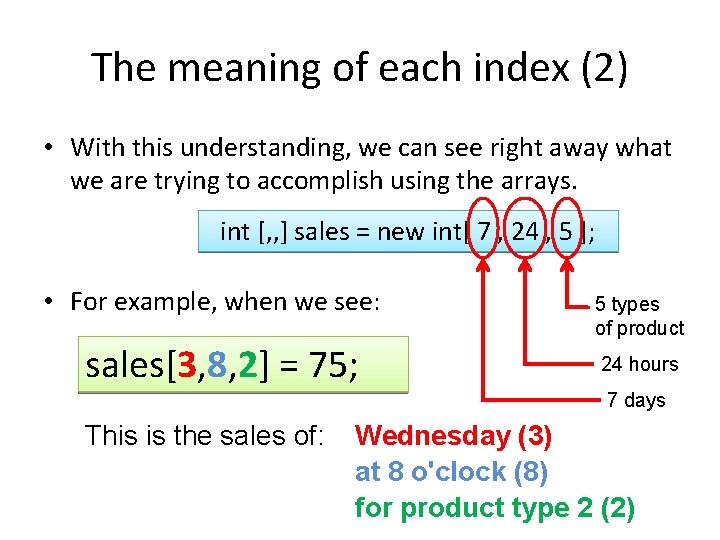
The meaning of each index (2) • With this understanding, we can see right away what we are trying to accomplish using the arrays. int [, , ] sales = new int[ 7 , 24 , 5 ]; • For example, when we see: sales[3, 8, 2] = 75; 5 types of product 24 hours 7 days This is the sales of: Wednesday (3) at 8 o'clock (8) for product type 2 (2)

Property Rank • To distinguish between arrays with different dimensions, we can use property Rank. string [] a = new string[100]; double [, ] b = new double[10, 20]; int [, , ] c = new int[5, 10, 20]; a. Rank 1 b. Rank 2 c. Rank 3

Conclusions

Conclusion • To store table-like data, we can use 2 D arrays. • If our data have more indices, we can use arrays with higher dimensions. • Useful for arrays: – Method Get. Length – Properties Length, and Rank. • It is helpful to try to understand nested loop from inside out.