Multicolored Subgraphs in an Edge Colored Graph HungLin

Multicolored Subgraphs in an Edge Colored Graph Hung-Lin Fu Department of Applied Mathematics NCTU, Hsin Chu, Taiwan 30050

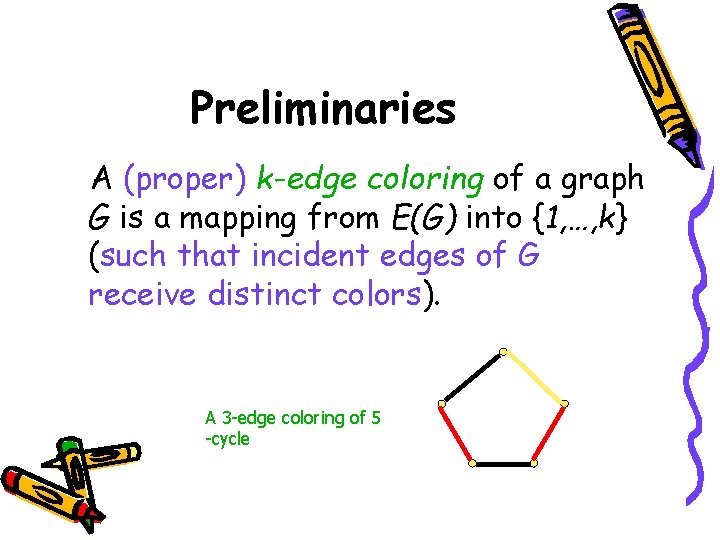
Preliminaries A (proper) k-edge coloring of a graph G is a mapping from E(G) into {1, …, k} (such that incident edges of G receive distinct colors). A 3 -edge coloring of 5 -cycle

Facts on Edge-Colorings • Let G be a simple graph with maximum degree (G). Then, the minimum number of colors needed to properly color G, (G), is either (G) or (G) + 1. (Vizing’s Theorem) • G is of class one if (G) = (G) and class two otherwise. • Kn is of class one if and only if n is even. • Kn, n is of class one.

Rainbow Subgraph • Let G be an edge-colored graph. Then a subgraph whose edges are of distinct colors is called a rainbow subgraph of G. • It is also known as a heterochromatic subgraph or a multicolored subgraph. • Note that the edge-coloring of the edgecolored graph may not be proper. • In this talk, all edge-colorings are proper edge-colorings. Therefore, a rainbow star can be found easily.

Rainbow 1 -factor Theorem (Woolbright and Fu, JCD 1998) In any (2 m-1)-edge-colored K 2 m where m > 2, there exists a rainbow 1 -factor. Conjecture (Transversal) In any n-edge-colored Kn, n, there exists a rainbow 1 -factor for each odd integer n.

Room Squares • A Room square of side 2 m-1 provides a (2 m -1)-edge-coloring of K 2 m such that 2 m-1 edge- disjoint multicolored 1 -factors exist. 35 17 28 46 26 48 15 37 13 57 68 24 47 16 38 25 58 23 14 67 12 78 56 34 36 45 27 18

Orthogonal Latin Squares • A Latin square of order n corresponds to an n-edge-coloring of Kn, n. • A Latin square of order n with an orthogonal mate provides n edge-disjoint multicolored 1 -factors of Kn, n. 1 2 3 2 3 1 2 2 3 1

Multicolored Subgraph • Conjecture Given an (n-1)-edgecolored Kn for even n > n 0, a multicolored Hamiltonian path exists. (By whom? ) • How about multicolored spanning trees?

Brualdi-Hollingsworth’s Conjecture If m>2, then in any proper edge coloring of K 2 m with 2 m-1 colors, all edges can be partitioned into m multicolored spanning trees.

Multicolored Tree Parallelism • K 2 m admits a multicolored tree parallelism (MTP) if there exists a proper (2 m-1)-edge-coloring of K 2 m for which all edges can be partitioned into m isomorphic multicolored spanning trees.

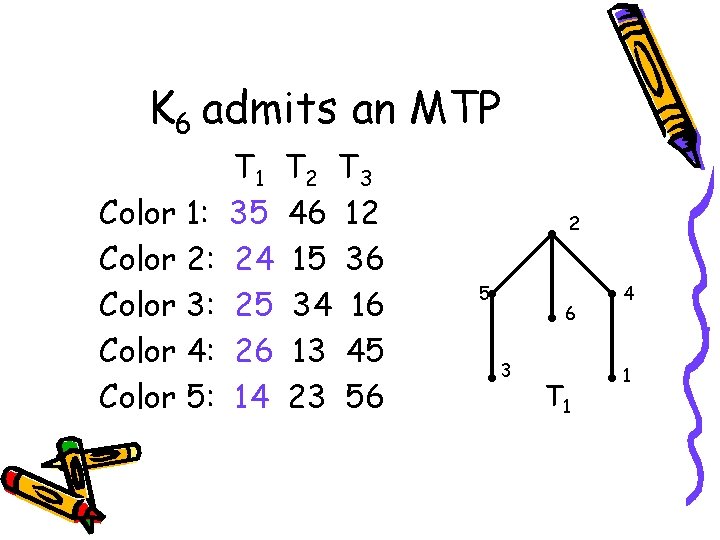
K 6 admits an MTP Color 1: Color 2: Color 3: Color 4: Color 5: T 1 35 24 25 26 14 T 2 T 3 46 12 15 36 34 16 13 45 23 56 2 5 6 3 T 1 4 1

Two Conjectures on MTP Constantine’s Weak Conjecture For any natural number m > 2, there exists a (2 m-1)-edgecoloring of K 2 m for which K 2 m can be decomposed into m multicolored isomorphic spanning trees.

Constantine’s Strong Conjecture If m > 2, then in any proper edge coloring of K 2 m with 2 m-1 colors, all edges can be partitioned into m isomorphic multicolored spanning trees. (Three, so far!)

Theorem (Akbari, Alipour, Fu and Lo) For m is an odd positive integer, then K 2 m admits an MTP. Fact. Constantine’s Weak Conjecture is true.

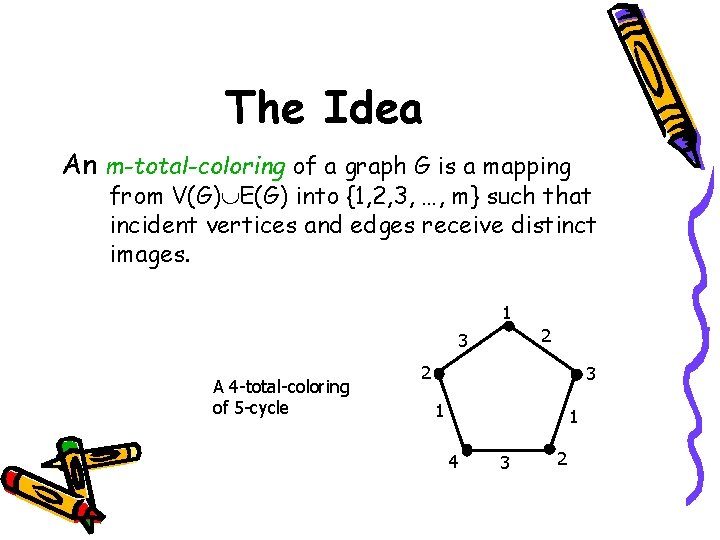
The Idea An m-total-coloring of a graph G is a mapping from V(G) E(G) into {1, 2, 3, …, m} such that incident vertices and edges receive distinct images. 1 2 3 A 4 -total-coloring of 5 -cycle 2 3 1 1 4 3 2

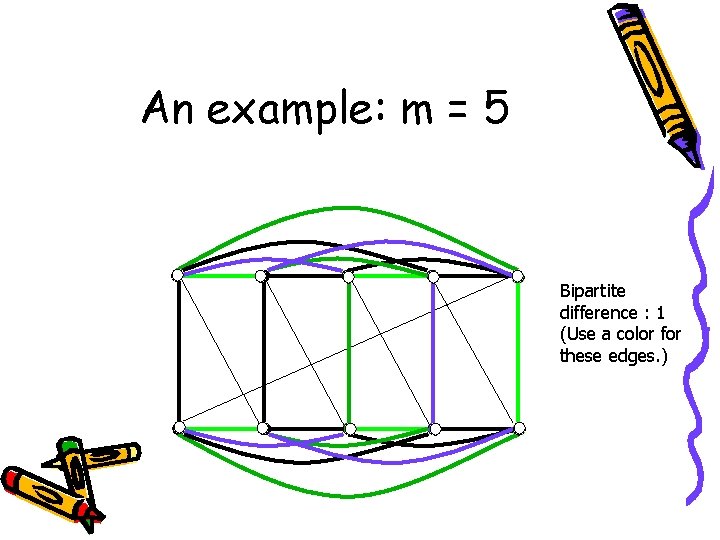
An example: m = 5 Bipartite difference : 1 (Use a color for these edges. )

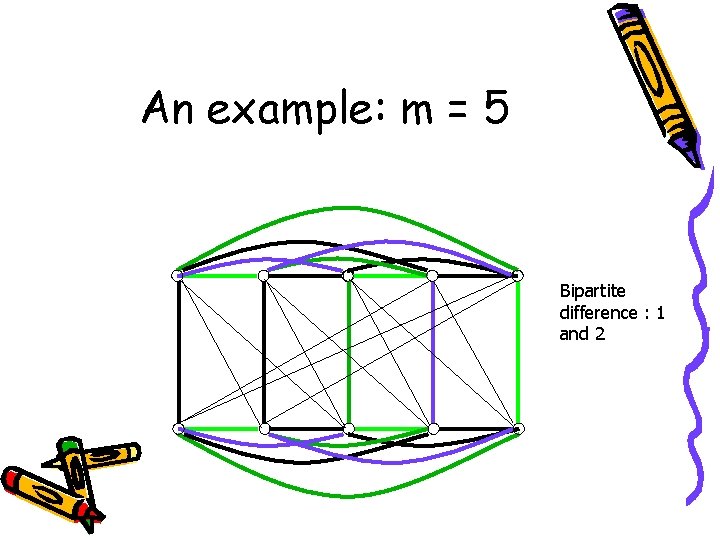
An example: m = 5 Bipartite difference : 1 and 2

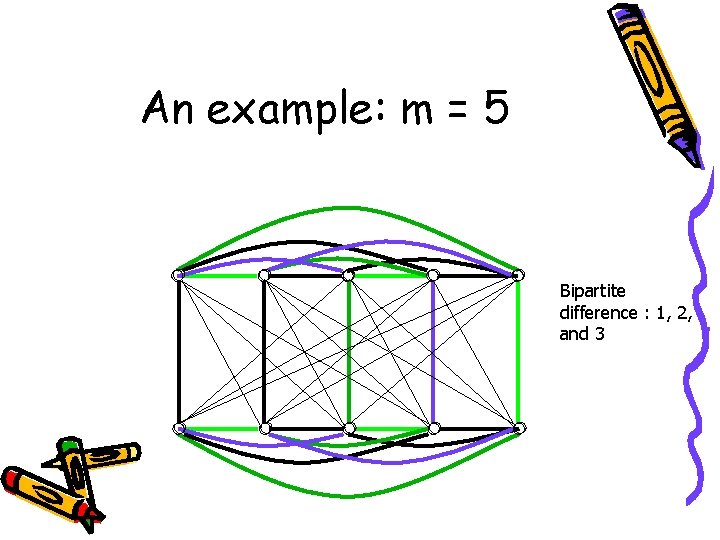
An example: m = 5 Bipartite difference : 1, 2, and 3

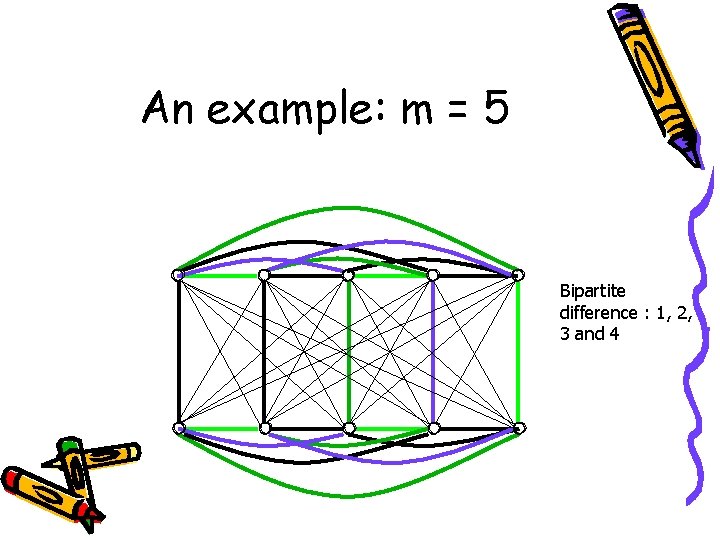
An example: m = 5 Bipartite difference : 1, 2, 3 and 4

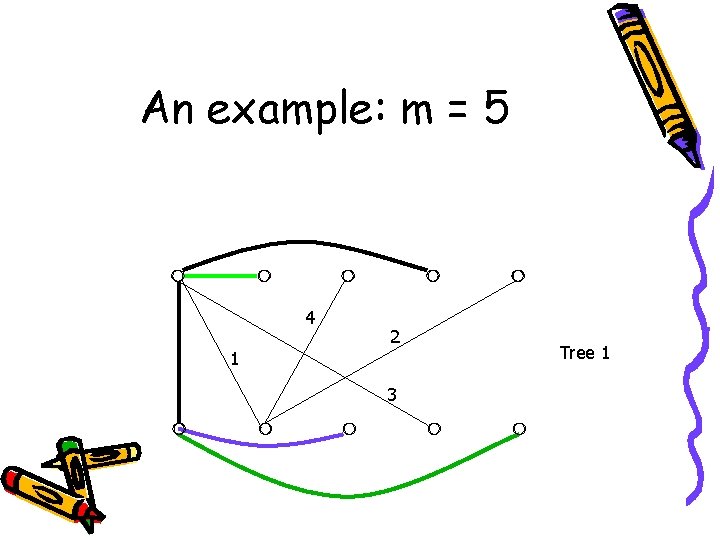
An example: m = 5 4 2 1 3 Tree 1

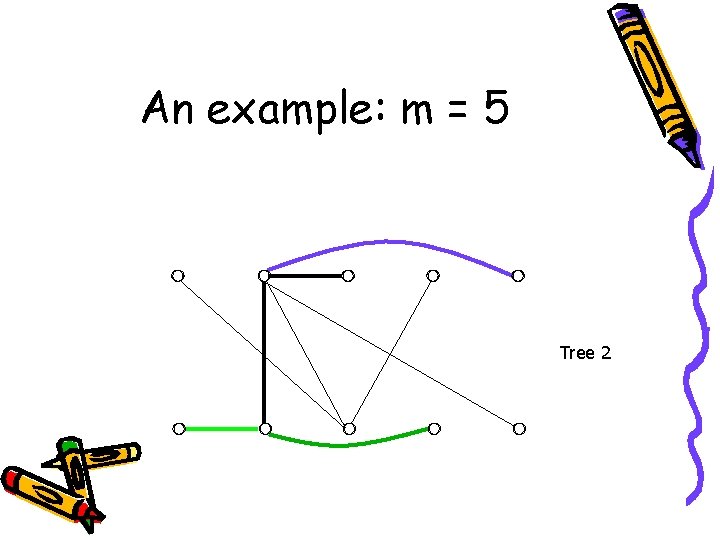
An example: m = 5 Tree 2

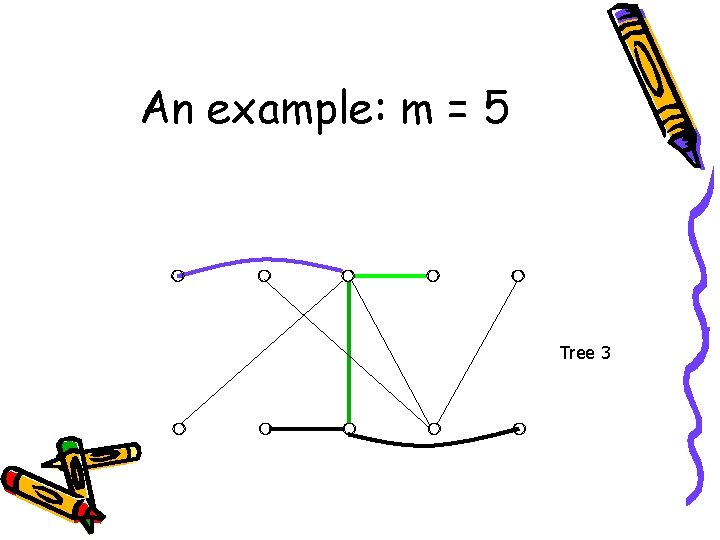
An example: m = 5 Tree 3

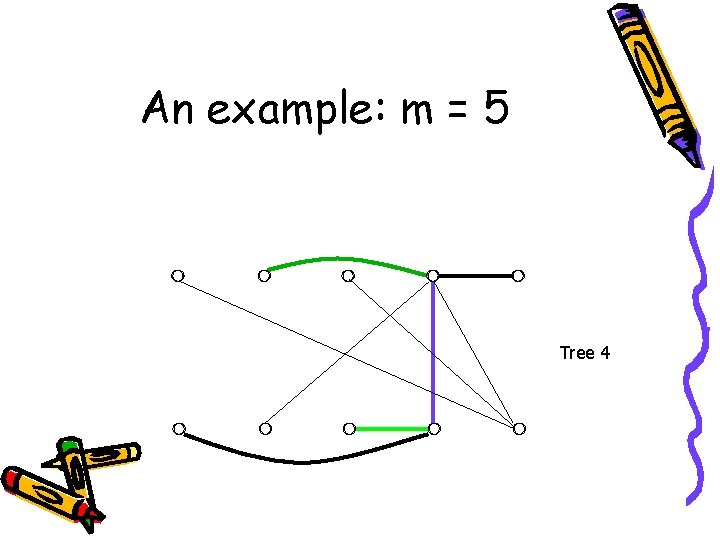
An example: m = 5 Tree 4

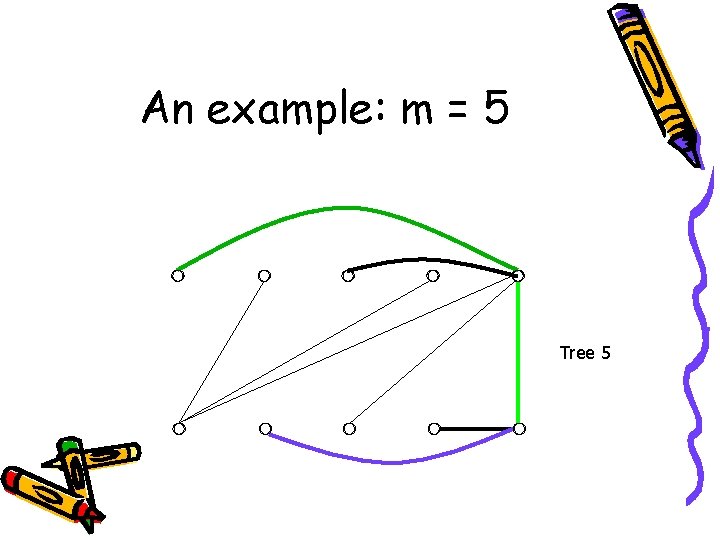
An example: m = 5 Tree 5

An example: m = 5 These trees are isomorphic to : Done!

Edge-colored Kn, n is Odd • It is well known that Kn is of class 2 when n is odd, i. e. the chromatic index of Kn is n. • In order to find multicolored parallelism, each subgraph has to be of size n. The best candidate is therefore the Hamiltonian cycles of K n.

MHCP • K 2 m+1 admits a multicolored Hamiltonian cycle parallelism (MHCP) if there exists a proper (2 m+1)-edge-coloring of K 2 m+1 for which all edges can be partitioned into m multicolored Hamiltonian cycles.

The Existence • Theorem (Constantine, SIAM DM) If n is an odd prime, then Kn admits an MHCP. • Conjecture Kn admits an MHCP for each odd integer n.

MHCP Lemma (Fu and Lo, DM) Let v be a composite odd integer and n is the smallest prime which is a factor of v, say v = mn. If Km admits an MHCP, then Km(n) admits an MHCP.

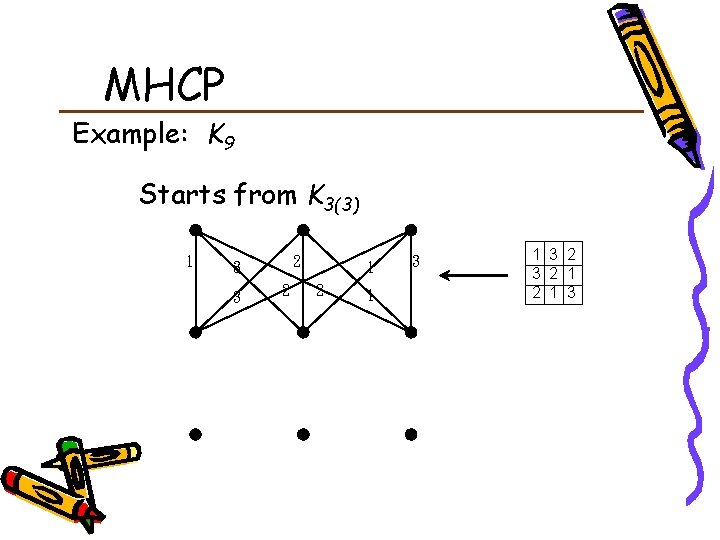
MHCP Example: K 9 Starts from K 3(3) 1 2 3 3 2 1 3 1 3 2 1 2 1 3

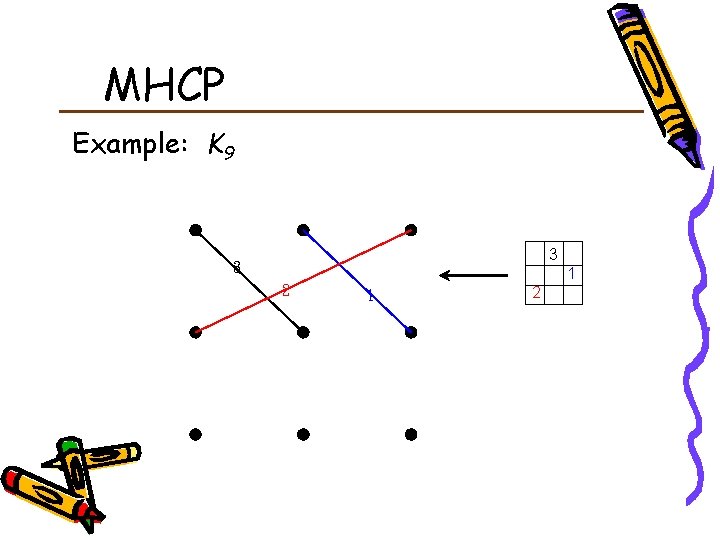
MHCP Example: K 9 3 3 2 1 1 2

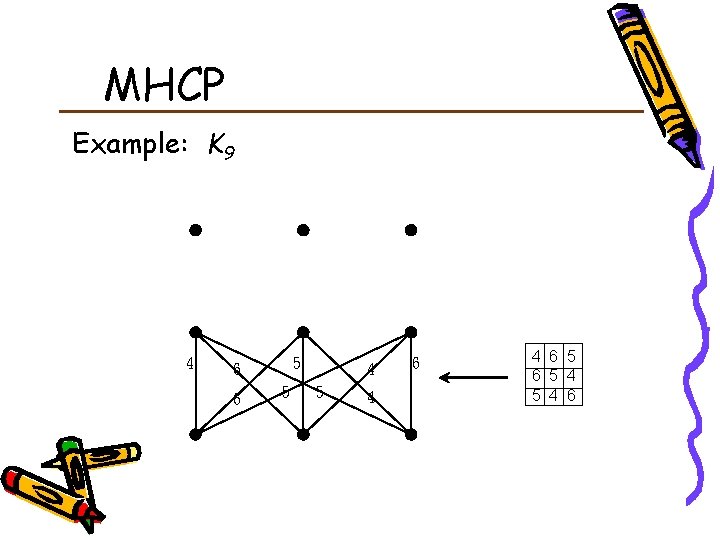
MHCP Example: K 9 4 5 6 6 5 4 6 4 6 5 4 5 4 6

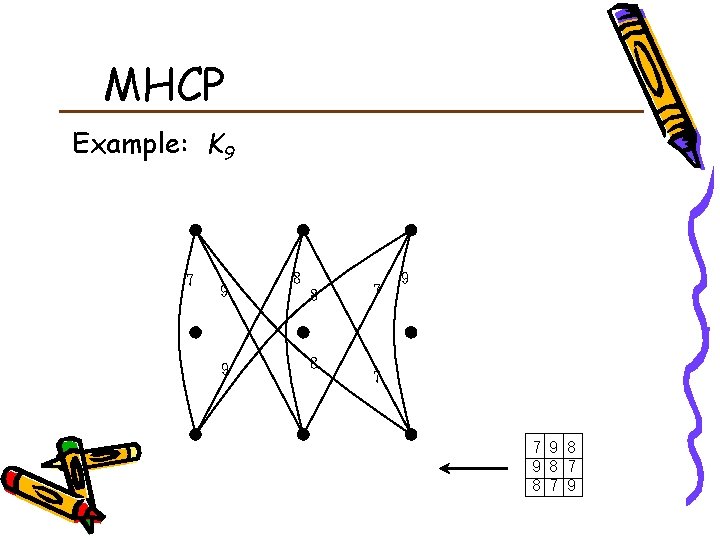
MHCP Example: K 9 7 9 9 8 8 8 7 9 7 7 9 8 7 8 7 9

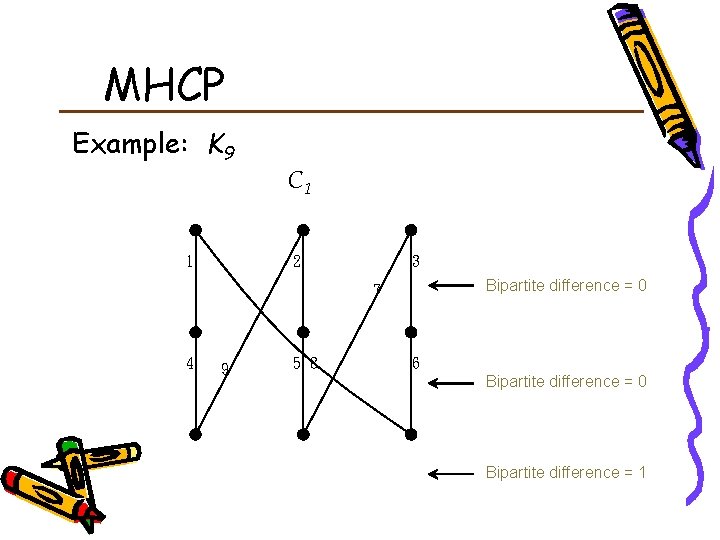
MHCP Example: K 9 1 C 1 2 3 Bipartite difference = 0 7 4 9 5 8 6 Bipartite difference = 0 Bipartite difference = 1

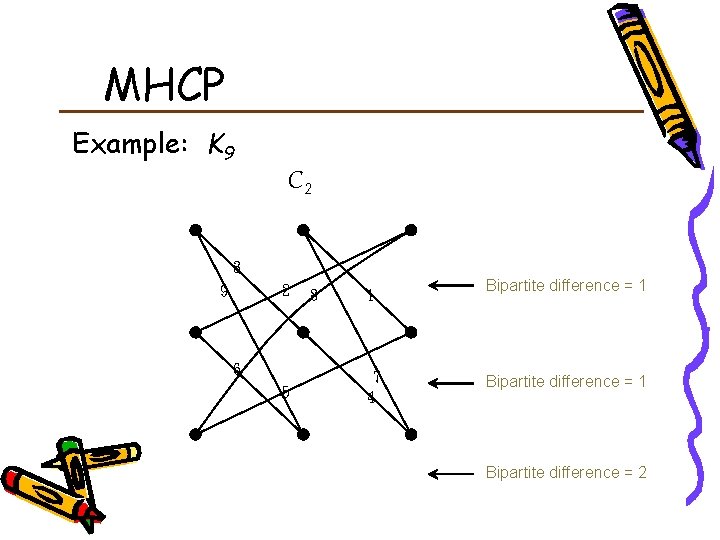
MHCP Example: K 9 C 2 3 2 9 6 5 8 1 7 4 Bipartite difference = 1 Bipartite difference = 2

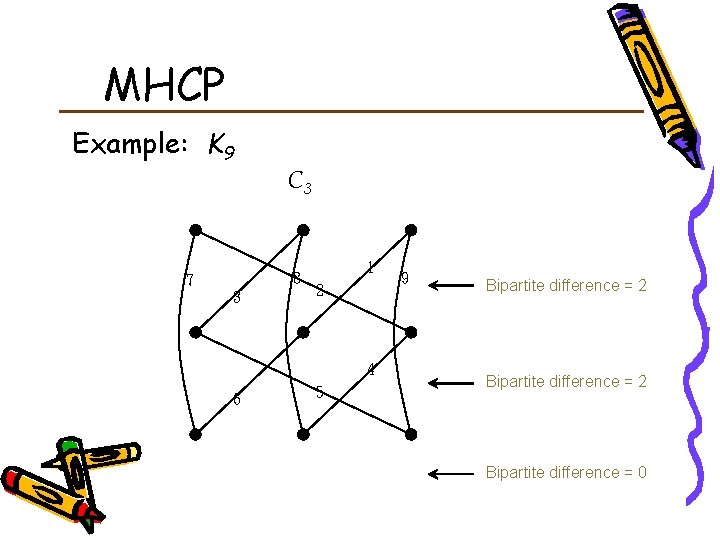
MHCP Example: K 9 C 3 8 7 3 1 2 4 6 5 9 Bipartite difference = 2 Bipartite difference = 0

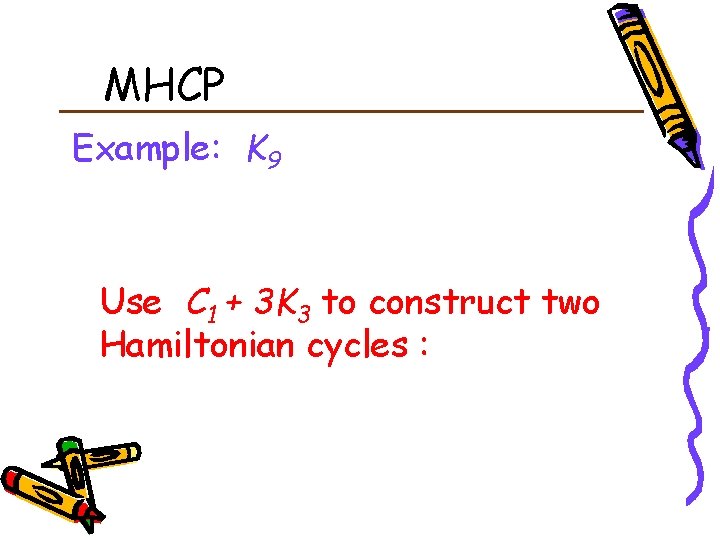
MHCP Example: K 9 Use C 1 + 3 K 3 to construct two Hamiltonian cycles :

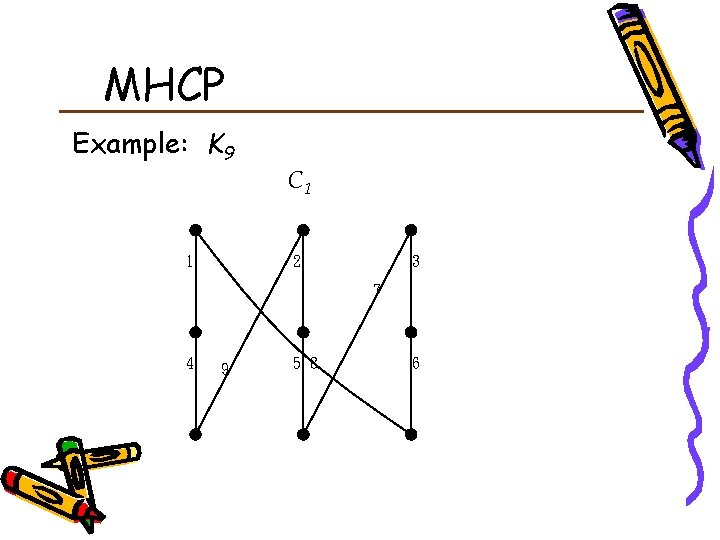
MHCP Example: K 9 1 C 1 2 3 7 4 9 5 8 6

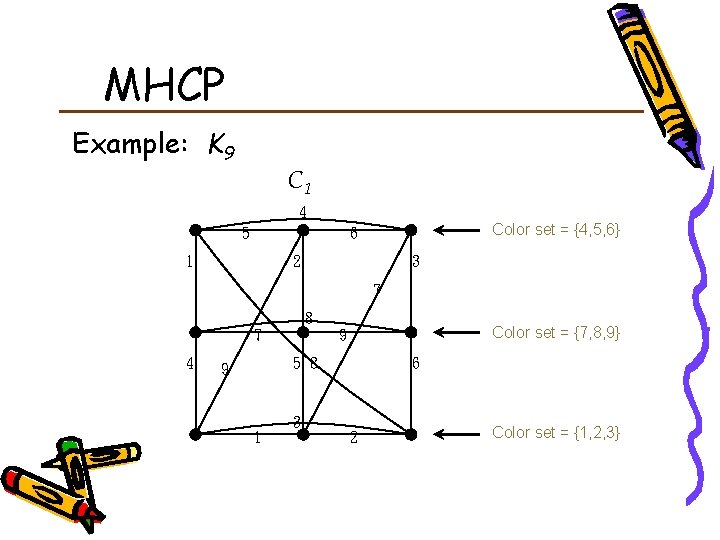
MHCP Example: K 9 C 1 4 5 Color set = {4, 5, 6} 6 1 2 3 7 8 7 4 Color set = {7, 8, 9} 9 5 8 9 1 3 6 2 Color set = {1, 2, 3}

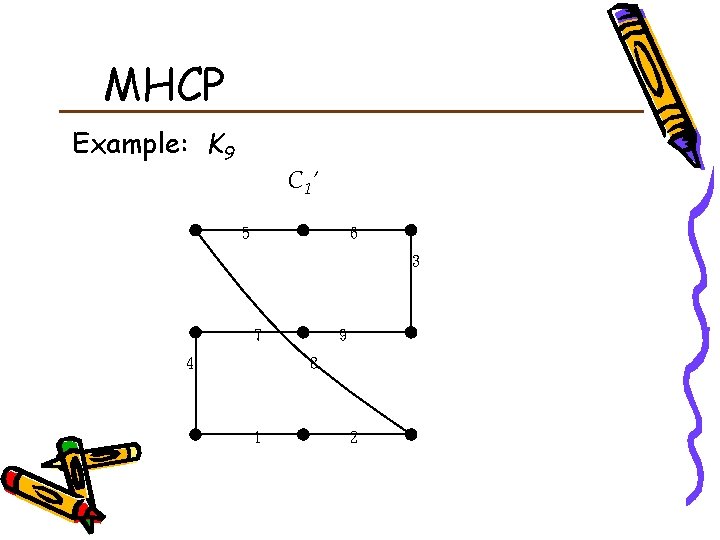
MHCP Example: K 9 C 1’ 5 6 3 7 9 8 4 1 2

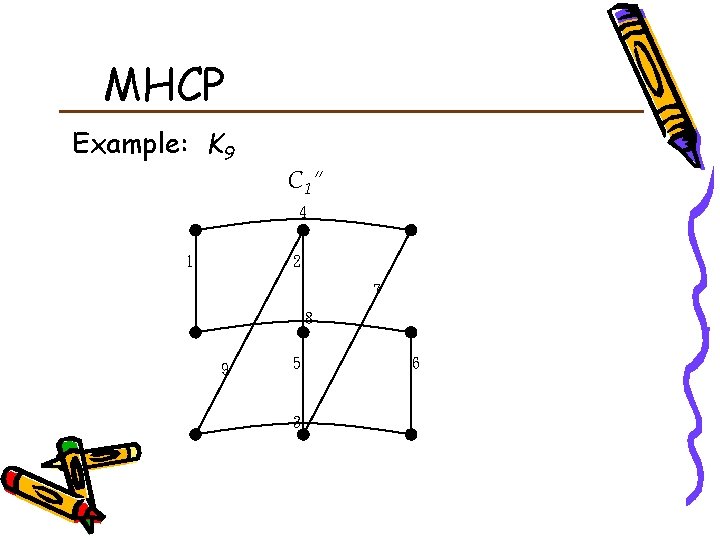
MHCP Example: K 9 C 1” 4 1 2 7 8 9 5 3 6

Not Many Are found in General • Let μ be an arbitrary (2 m-1)-edgecoloring of K 2 m. Then there exist three isomorphic multicolored spanning trees in K 2 m for m > 2. • Joint work with Y. H. Lo.

Observation • If the edge-coloring is arbitrarily given, then the proof of finding MTP is going to be very difficult. • If we drop “isomorphism” for the above case, then can we find m multicolored spanning trees of K 2 m?

Problem: How many multicolored spanning trees of an edge-colored K 2 m can we find if m is getting larger? • Guess? is m. Of course, the best result

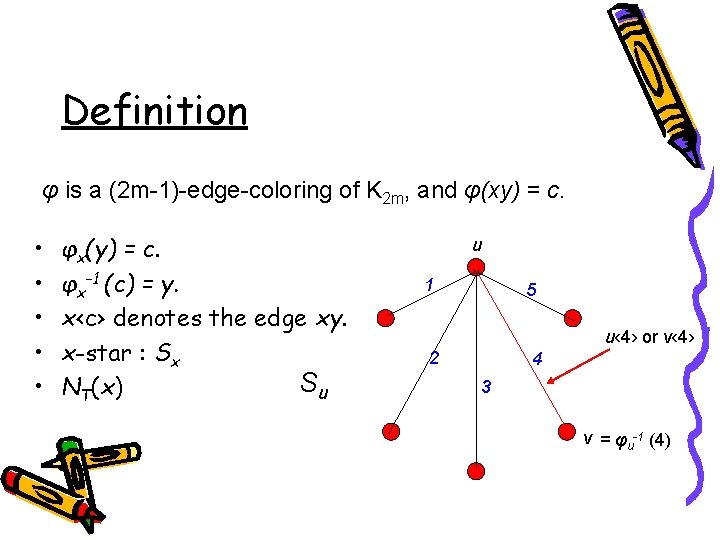
Definition φ is a (2 m-1)-edge-coloring of K 2 m, and φ(xy) = c. • • • φx(y) = c. φx-1 (c) = y. x‹c› denotes the edge xy. x-star : Sx Su NT(x) u 1 5 u‹ 4› or v‹ 4› 2 4 3 v = φu-1 (4)

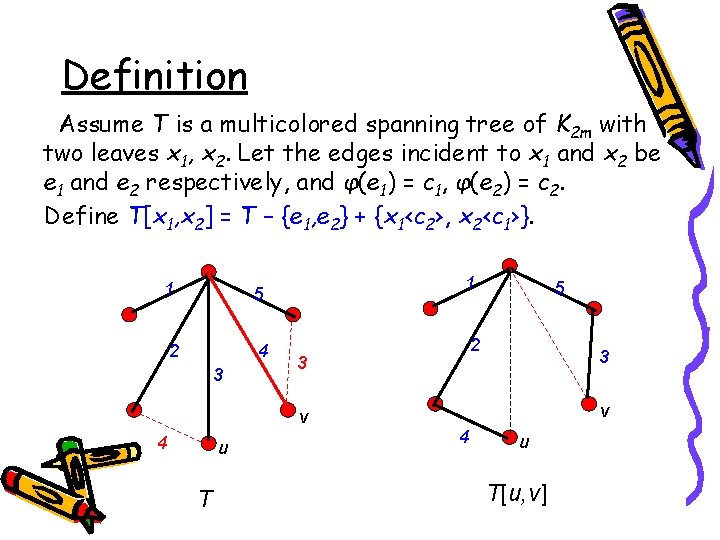
Definition Assume T is a multicolored spanning tree of K 2 m with two leaves x 1, x 2. Let the edges incident to x 1 and x 2 be e 1 and e 2 respectively, and φ(e 1) = c 1, φ(e 2) = c 2. Define T[x 1, x 2] = T – {e 1, e 2} + {x 1‹c 2›, x 2‹c 1›}. 1 5 2 4 3 1 4 u T 2 3 v 5 3 v 4 u T[u, v]

Definition T is a set of mutually disjoint multicolored spanning trees in a (2 m-1)-edge-colored K 2 m. A multicolored spanning tree T is said to be feasible for T if the union of trees in T and T are disjoint.

Constructing Process T = {T 1, …, Tn}, xi is the root of Ti. Let U = 1. Pick u 2. Choose v 1 T T 1. 3. For 2 ≤ I ≤ n, choose vi U {u} s. t. Ti [u, vi] is feasible for T Ti and (1) …, (2)…, (3)…… 4. Redefine Ti = Ti [u, vi] and let Tn+1 = Su [u 1, u 2, …, un]. U, and let φ(uxi ) = i. U {u} s. t. T 1[u, v 1] is feasible for

Constructing Process x 1 x 3 x 2 U x 4 x 5

Constructing Process x 1 x 2 1 2 x 3 3 u x 4 4 5 x 5

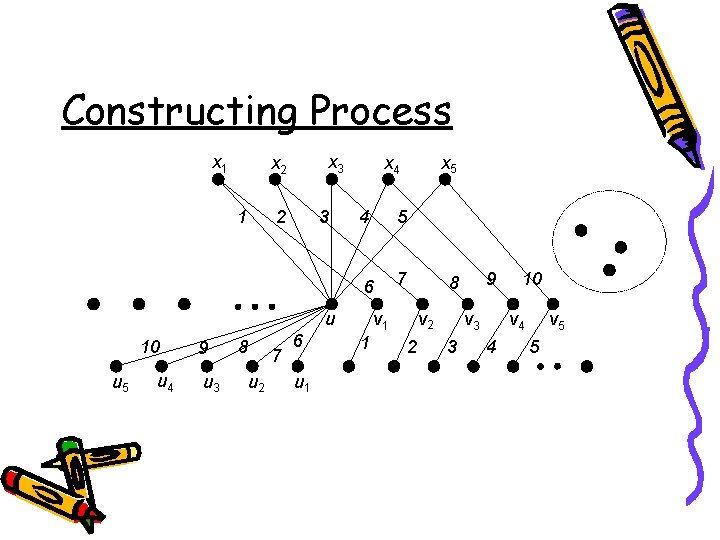
Constructing Process x 1 x 3 x 2 1 2 3 4 5 6 7 u 10 u 5 u 4 9 u 3 8 7 u 2 6 u 1 x 5 x 4 v 2 v 1 1 9 8 2 v 3 3 10 v 4 4 v 5 5

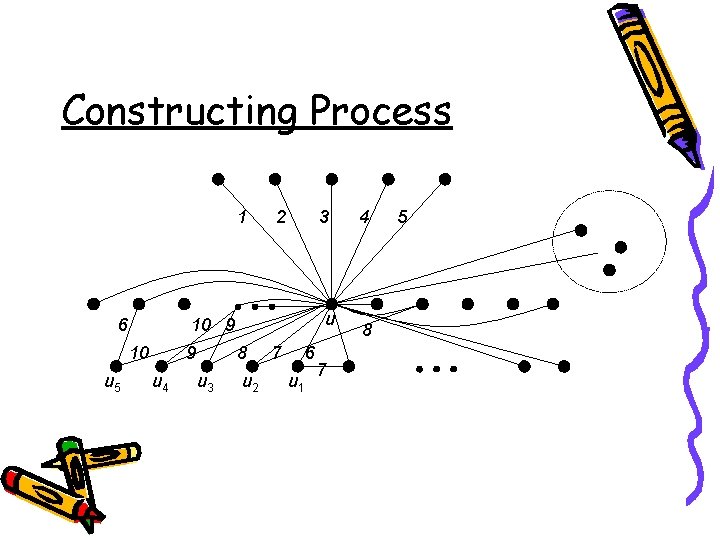
Constructing Process 1 6 3 u 10 9 10 u 5 2 8 9 u 4 u 3 u 2 7 6 u 1 7 4 8 5

Note 1. Colors 6~10 are distinct. 2. v 1‹ 7›, v 2‹ 8›, v 3‹ 9›, v 4‹ 10›, v 5‹ 6› are not incident to x 1 ~ x 5. 3. v 1‹ 7›, v 2‹ 8›, v 3‹ 9›, v 4‹ 10›, v 5‹ 6› can not form a cycle. In order to get vn, |U| ≥ 6 n-4.

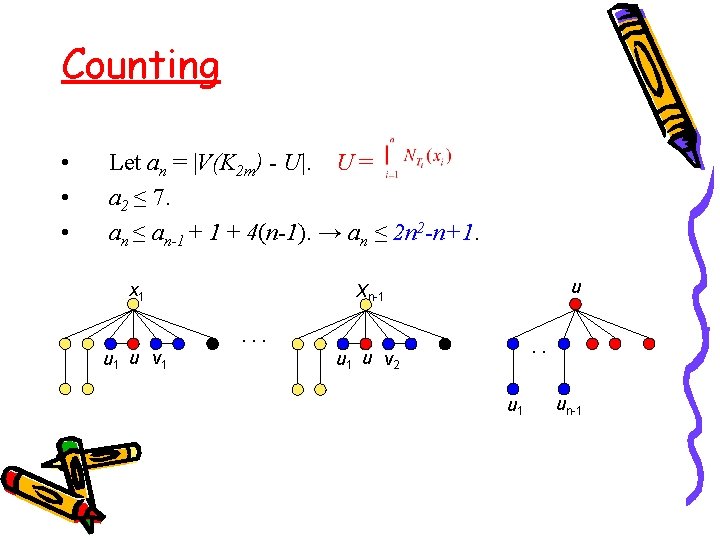
Counting • • • Let an = |V(K 2 m) - U|. U = a 2 ≤ 7. an ≤ an-1 + 4(n-1). → an ≤ 2 n 2 -n+1. x 1 u Xn-1. . . u 1 u v 1 . . u 1 u v 2 u 1 un-1

Theorem (with Y. H. Lo) • For m large enough, we can find at least about (2 m)1/2 multicolored spanning trees in (2 m-1)-edge-colored K 2 m.

Don’t Stop!

We Have to Stop! Never Ever Give Up!!

• Thank you for your attention!

th 60 Happy Birthday to 藤原 良教授