Multiclass Classification in NLP n NameEntity Recognition Label

Multiclass Classification in NLP n Name/Entity Recognition Label people, locations, and organizations in a sentence ¨ [PER Sam Houston], [born in] [LOC Virginia], [was a member of the] [ORG US Congress]. ¨ n Decompose into sub-problems ¨ Sam Houston, born in Virginia. . . (1) ¨ Sam Houston, born in Virginia. . . (0) ¨ Sam Houston, born in Virginia. . . (2) n (PER, LOC, ORG, ? ) PER (PER, LOC, ORG, ? ) None (PER, LOC, ORG, ? ) LOC Many problems in NLP are decomposed this way ¨ Disambiguation tasks n n n ¨ POS Tagging Word-sense disambiguation Verb Classification Semantic-Role Labeling 1

Outline n Multi-Categorical Classification Tasks ¨ n n Decomposition Approaches Constraint Classification ¨ n example: Semantic Role Labeling (SRL) Unifies learning of multi-categorical classifiers Structured-Output Learning ¨ revisit SRL n Decomposition versus Constraint Classification n Goal: Discuss multi-class and structured output from the same perspective. ¨ Discuss similarities and differences ¨ 2

Multi-Categorical Output Tasks n Multi-class Classification (y {1, . . . , K}) character recognition (‘ 6’) document classification (‘homepage’) n Multi-label Classification (y {1, . . . , K}) document classification (‘(homepage, facultypage)’) n Category Ranking (y K) user preference (‘(love > like > hate)’) document classification (‘hompage > facultypage > sports’) n Hierarchical Classification (y {1, . . , K}) cohere with class hierarchy place document into index where ‘soccer’ is-a ‘sport’ 3

(more) Multi-Categorical Output Tasks n Sequential Prediction (y {1, . . . , K}+) e. g. POS tagging (‘(NVNNA)’) “This is a sentence. ” D V N D e. g. phrase identification Many labels: KL for length L sentence n Structured Output Prediction (y C({1, . . . , K}+)) e. g. parse tree, multi-level phrase identification e. g. sequential prediction Constrained by domain, problem, data, background knowledge, etc. . . 4

Semantic Role Labeling A Structured-Output Problem n For each verb in a sentence Identify all constituents that fill a semantic role Determine their roles 1. 2. • • Core Arguments, e. g. , Agent, Patient or Instrument Their adjuncts, e. g. , Locative, Temporal or Manner A 0 : leaver A 2 : benefactor I left my pearls to my daughter-in-law in my will. A 1 : thing left AM-LOC 5

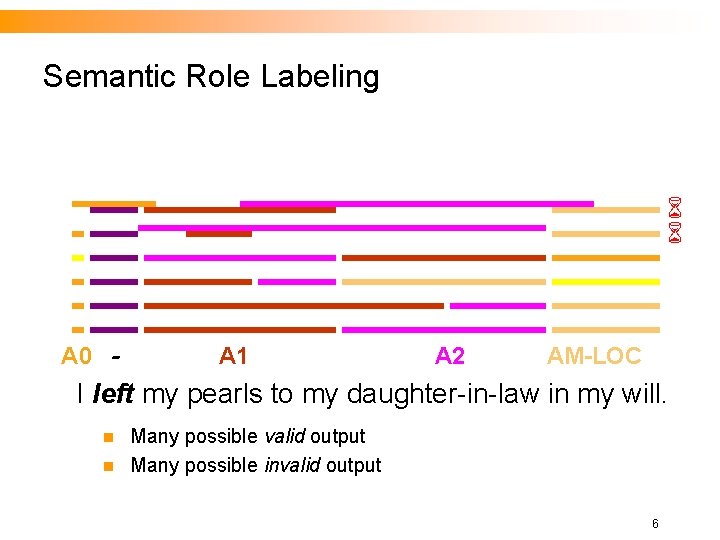
Semantic Role Labeling A 0 - A 1 A 2 AM-LOC I left my pearls to my daughter-in-law in my will. n n Many possible valid output Many possible invalid output 6

Structured Output Problems n Multi-Class View y=4 as (y 1, . . . , yk) = ( 0 0 0 1 0 0 0 ) ¨ The output is restricted by “Exactly one of yi=1” ¨ Learn f 1(x), . . , fk(x) ¨ n Sequence Prediction e. g. POS tagging: x = (My name is Dav) y = (Pr, N, V, N) ¨ e. g. restriction: “Every sentence must have a verb” ¨ n Structured Output Arbitrary global constraints ¨ Local functions do not have access to global constraints! ¨ n Goal: Discuss multi-class and structured output from the same perspective. ¨ Discuss similarities and differences ¨ 7

Transform the sub-problems n Sam Houston, born in Virginia. . . (PER, LOC, ORG, ? ) PER (1) n Transform each problem to feature vector ¨ n Sam Houston, born in Virginia (Bob-, JOHN-, SAM HOUSTON, HAPPY, -BORN, --BORN, . . . ) ( 0 , 1 , . . . ) Transform each label to a class label PER ¨ LOC ¨ ORG ¨ ? ¨ n n Input : Output: 0 1 2 3 {0, 1}d or Rd {0, 1, 2, 3, . . . , k} 8

Solving multiclass with binary learning n Multiclassifier ¨ Function f : Rd {1, 2, 3, . . . , k} n Decompose into binary problems n Not always possible to learn No theoretical justification (unless the problem is easy) n 9

The Real Multi. Class Problem n General framework Extend binary algorithms ¨ Theoretically justified ¨ n n ¨ n Provably correct Generalizes well Verified Experimentally Naturally extends binary classification algorithms to mulitclass setting ¨ e. g. Linear binary separation induces linear boundaries in multiclass setting 10

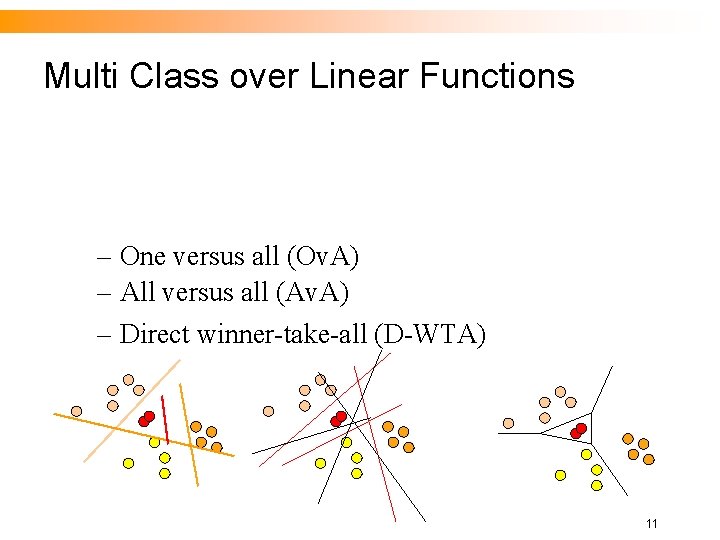
Multi Class over Linear Functions – One versus all (Ov. A) – All versus all (Av. A) – Direct winner-take-all (D-WTA) 11

WTA over linear functions n Assume examples generated from winner-take-all y = argmax wi. x + ti ¨ wi, x Rn , ti R ¨ • Note: Voronoi diagrams are WTA functions argminc || ci – x || = argmaxc ci. x – ||ci||2 / 2 12

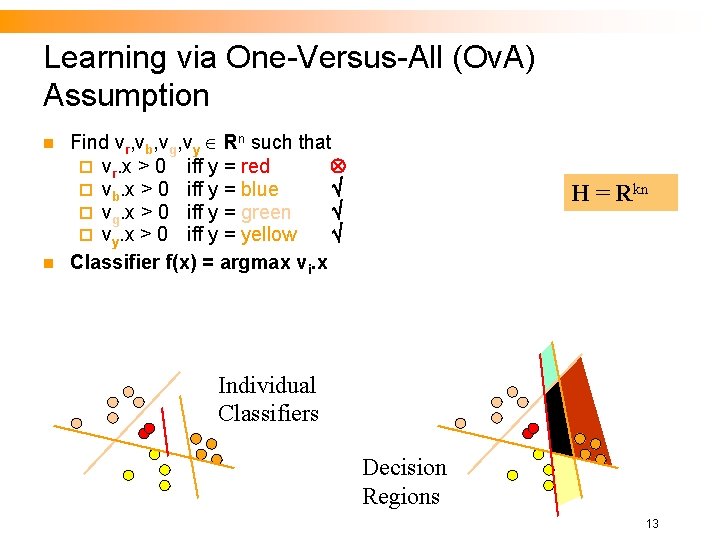
Learning via One-Versus-All (Ov. A) Assumption n n Find vr, vb, vg, vy Rn such that ¨ vr. x > 0 iff y = red ¨ vb. x > 0 iff y = blue ¨ vg. x > 0 iff y = green ¨ vy. x > 0 iff y = yellow Classifier f(x) = argmax vi. x H = Rkn Individual Classifiers Decision Regions 13

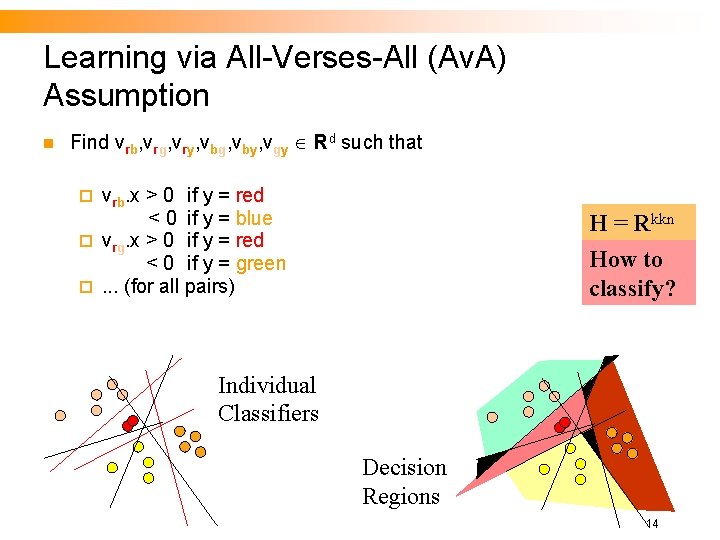
Learning via All-Verses-All (Av. A) Assumption n Find vrb, vrg, vry, vbg, vby, vgy Rd such that vrb. x > 0 if y = red < 0 if y = blue ¨ vrg. x > 0 if y = red < 0 if y = green ¨. . . (for all pairs) ¨ H = Rkkn How to classify? Individual Classifiers Decision Regions 14

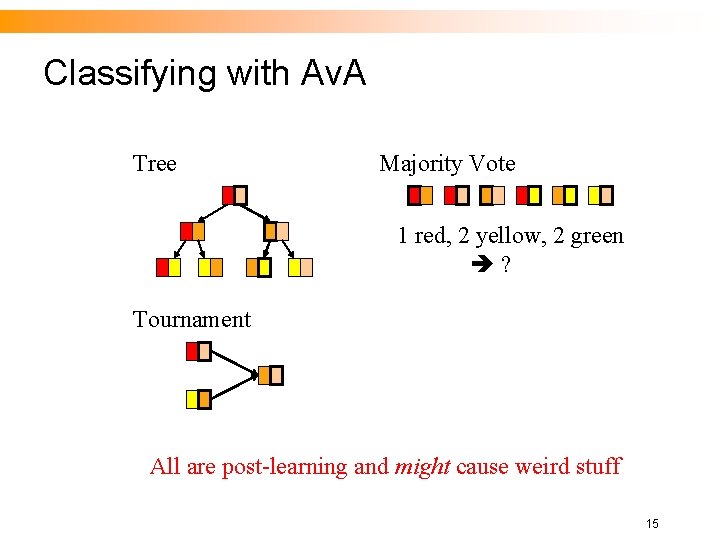
Classifying with Av. A Tree Majority Vote 1 red, 2 yellow, 2 green ? Tournament All are post-learning and might cause weird stuff 15

Summary (1): Learning Binary Classifiers n On-Line: Perceptron, Winnow Mistake bounded ¨ Generalizes well (VC-Dim) ¨ Works well in practice ¨ n SVM Well motivated to maximize margin ¨ Generalizes well ¨ Works well in practice ¨ n Boosting, Neural Networks, etc. . . 16

From Binary to Multi-categorical n Decompose multi-categorical problems ¨ n n into multiple (independent) binary problems Multi-class: Ov. A, Av. A, ECOC, DT, etc. . . Multi-label: reduce to multi-class Categorical Ranking: reduce or regression Sequence Prediction: Reduce to Multi-class ¨ part/alphabet based decompositions ¨ n Structured Output: ¨ learn parts of output based on local information!!! 17

Problems with Decompositions n Learning optimizes over local metrics ¨ Poor global performance n n n What is the metric? We don’t care about the performance of the local classifiers Poor decomposition poor performance Difficult local problems ¨ Irrelevant local problems ¨ n Not clear how to decompose all Multi-category problems 18

Multi-class Ov. A Decomposition: a Linear Representation n n Hypothesis: h(x) = argmaxi vix Decomposition ¨ n Learning: One-versus-all (Ov. A) ¨ n Each class represented by a linear function vix For each class i vix > 0 iff i=y General Case ¨ Each class represented by a function fi(x) > 0 19

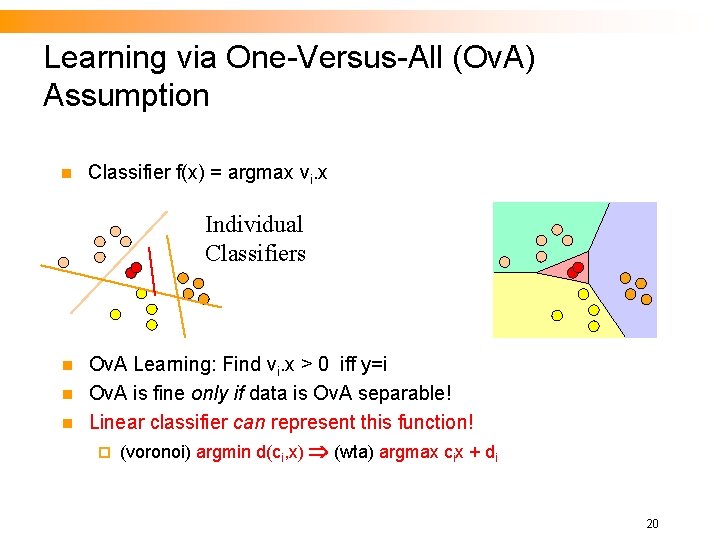
Learning via One-Versus-All (Ov. A) Assumption n Classifier f(x) = argmax vi. x Individual Classifiers n n n Ov. A Learning: Find vi. x > 0 iff y=i Ov. A is fine only if data is Ov. A separable! Linear classifier can represent this function! ¨ (voronoi) argmin d(ci, x) (wta) argmax cix + di 20

Other Issues we Mentioned n Error Correcting Output Codes Another (class of) decomposition ¨ Difficulty: how to make sure that the resulting problems are separable. ¨ n Commented on the advantage of All vs. All when working with the dual space (e. g. , kernels) 21

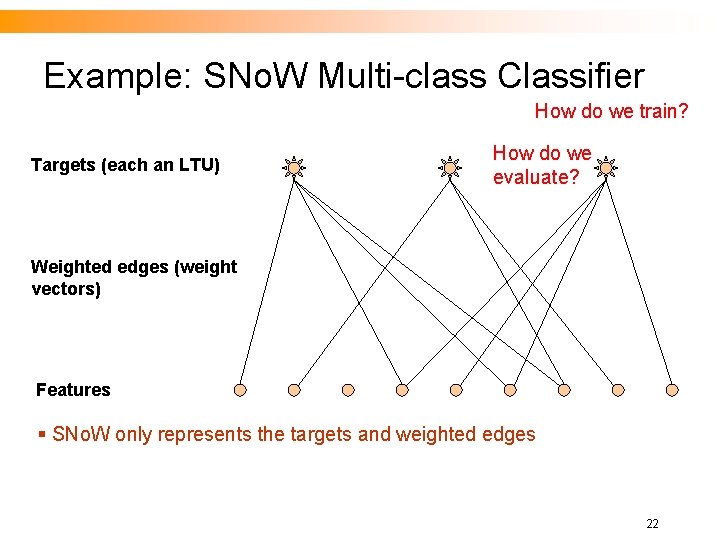
Example: SNo. W Multi-class Classifier How do we train? Targets (each an LTU) How do we evaluate? Weighted edges (weight vectors) Features § SNo. W only represents the targets and weighted edges 22

Winnow: Extensions n n Winnow learns monotone boolean functions To learn non-monotone boolean functions: For each variable x, introduce x’ = ¬x ¨ Learn monotone functions over 2 n variables ¨ n To learn functions with real valued inputs: “Balanced Winnow” ¨ 2 weights per variable; effective weight is the difference ¨ Update rule: ¨ 23

An Intuition: Balanced Winnow n n In most multi-classifiers you have a target node that represents positive examples and target node that represents negative examples. Typically, we train each node separately (my/not my example). Rather, given an example we could say: this is more a + example than a – example. We compared the activation of the different target nodes (classifiers) on a given example. (This example is more class + than class -) 24

Constraint Classification n n n Can be viewed as a generalization of the balanced Winnow to the multi-class case Unifies multi-class, multi-label, category-ranking Reduces learning to a single binary learning task Captures theoretical properties of binary algorithm Experimentally verified Naturally extends Perceptron, SVM, etc. . . Do all of this by representing labels as a set of constraints or preferences among output labels. 25

Multi-category to Constraint Classification n Multiclass ¨ n (x, (A>B, A>C, A>D) ) Multilabel ¨ n (x, A) (x, (A, B)) (x, ( (A>C, A>D, B>C, B>D) ) Label Ranking ¨ (x, (5>4>3>2>1)) (x, ( (5>4, 4>3, 3>2, 2>1) ) n Examples (x, y) y Sk Sk : partial order over class labels {1, . . . , k} ¨ defines “preference” relation ( > ) for class labeling n Constraint Classifier n h: X Sk 26

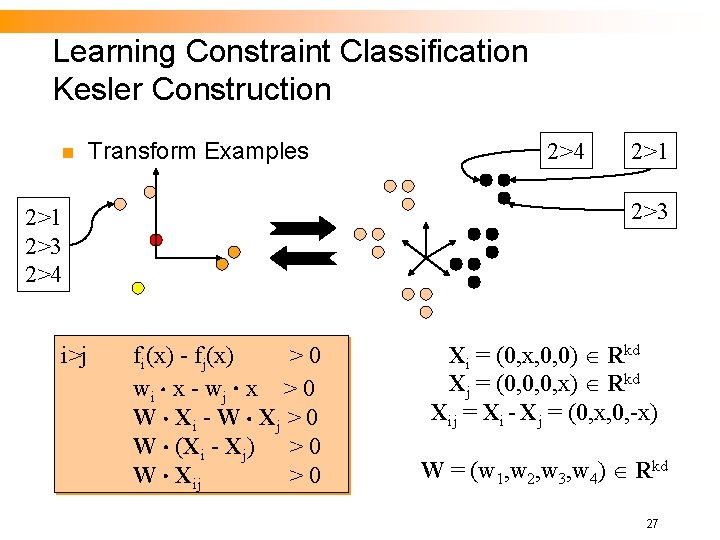
Learning Constraint Classification Kesler Construction n Transform Examples 2>1 2>3 2>4 i>j 2>4 fi(x) - fj(x) >0 wi x - wj x > 0 W Xi - W Xj > 0 W (Xi - Xj) > 0 W Xij >0 Xi = (0, x, 0, 0) Rkd Xj = (0, 0, 0, x) Rkd Xij = Xi - Xj = (0, x, 0, -x) W = (w 1, w 2, w 3, w 4) Rkd 27

Kesler’s Construction (1) n y = argmaxi=(r, b, g, y) vi. x ¨ n vi , x Rn Find vr, vb, vg, vy Rn such that vr. x > vb. x ¨ vr. x > vg. x ¨ vr. x > vy. x ¨ H = Rkn 28

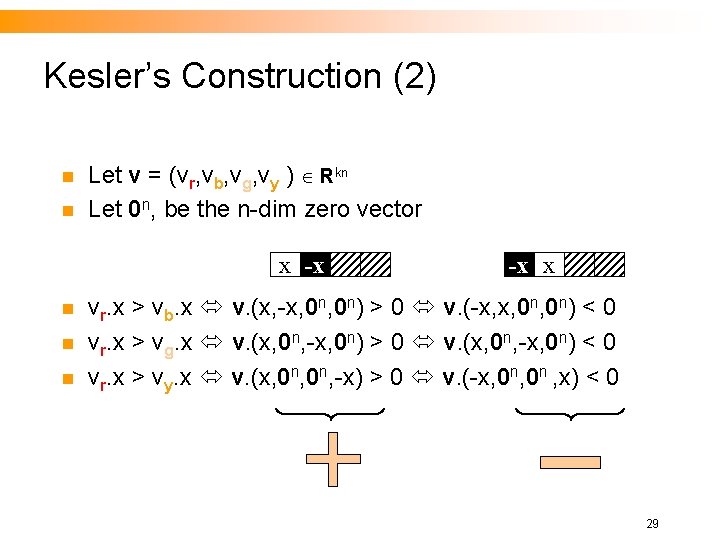
Kesler’s Construction (2) n n Let v = (vr, vb, vg, vy ) Rkn Let 0 n, be the n-dim zero vector x -x n n n -x x vr. x > vb. x v. (x, -x, 0 n) > 0 v. (-x, x, 0 n) < 0 vr. x > vg. x v. (x, 0 n, -x, 0 n) > 0 v. (x, 0 n, -x, 0 n) < 0 vr. x > vy. x v. (x, 0 n, -x) > 0 v. (-x, 0 n , x) < 0 29

Kesler’s Construction (3) n Let v = (v 1, . . . , vk) Rn x. . . x Rn = Rkn ¨ xij = (0(i-1)n, x, 0(k-i)n) – (0(j-1)n, –x, 0(k-j)n) Rkn ¨ n x Given (x, y) Rn x {1, . . . , k} ¨ For all j y n n -x Add to P+(x, y), (xyj, 1) Add to P-(x, y), (–xyj, -1) P+(x, y) has k-1 positive examples ( Rkn) P-(x, y) has k-1 negative examples ( Rkn) 30

Learning via Kesler’s Construction n n Given (x 1, y 1), . . . , (x. N, y. N) Rn x {1, . . . , k} Create P+ = P+(xi, yi) ¨ P– = P–(xi, yi) ¨ n Find v = (v 1, . . . , vk) Rkn, such that ¨ n v. x separates P+ from P– Output ¨ f(x) = argmax vi. x 31

Constraint Classification n Examples (x, y) ¨ n n y Sk Sk : partial order over class labels {1, . . . , k} ¨ defines “preference” relation (<) for class labels ¨ e. g. Multiclass: 2<1, 2<3, 2<4, 2<5 ¨ e. g. Multilabel: 1<3, 1<4, 1<5, 2<3, 2<4, 4<5 Constraint Classifier f: X Sk ¨ f(x) is a partial order ¨ ¨ f(x) is consistent with y if (i<j) y (i<j) f(x) 32

Implementation n Examples (x, y) ¨ n n n y Sk Sk : partial order over class labels {1, . . . , k} ¨ defines “preference” relation (>) for class labels ¨ e. g. Multiclass: 2>1, 2>3, 2>4, 2>5 Given an example that is labeled 2, the activation of target 2 on it, should be larger than the activation of the other targets. SNo. W implementation: Conservative. Only the target node that corresponds to the correct label and the highest activation are compared. ¨ If both are the same target node – no change. ¨ Otherwise, promote one and demote the other. ¨ 33

Properties of Construction n n Can learn any argmax vi. x function Can use any algorithm to find linear separation ¨ Perceptron Algorithm n ¨ Winnow Algorithm n n ultraconservative online algorithm [Crammer, Singer 2001] multiclass winnow [ Masterharm 2000 ] Defines a multiclass margin by binary margin in Rkd ¨ multiclass SVM [Crammer, Singer 2001] ¨ 34

Margin Generalization Bounds n Linear Hypothesis space: ¨ h(x) = argsort vi. x n n n vi, x Rd argsort returns permutation of {1, . . . , k} CC margin-based bound ¨ n n = min(x, y) S min (i < j) y vi. x – vj. x m - number of examples R - maxx ||x|| - confidence C - average # constraints 35

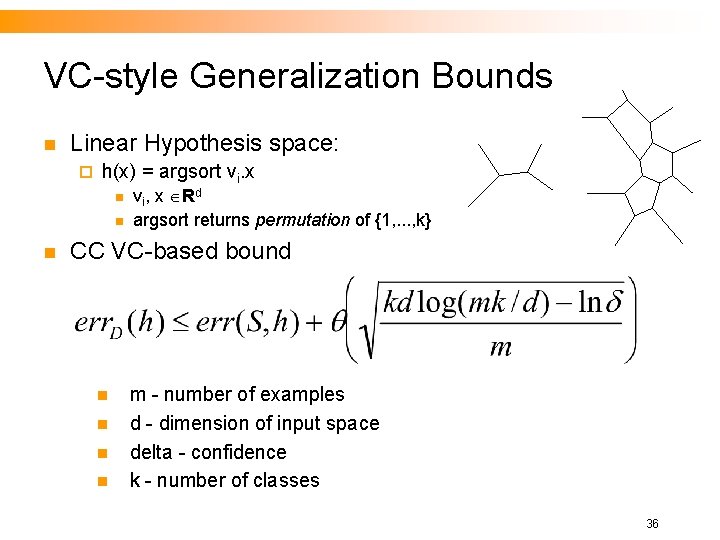
VC-style Generalization Bounds n Linear Hypothesis space: ¨ h(x) = argsort vi. x n n n vi, x Rd argsort returns permutation of {1, . . . , k} CC VC-based bound n n m - number of examples d - dimension of input space delta - confidence k - number of classes 36

Beyond Multiclass Classification n Ranking category ranking (over classes) ¨ ordinal regression (over examples) ¨ n Multilabel ¨ n Complex relationships ¨ n n n x is more red than blue, but not green Millions of classes ¨ n x is both red and blue sequence labeling (e. g. POS tagging) LATER SNo. W has an implementation of Constraint Classification for the Multi-Class case. Try to compare with 1 -vs-all. Experimental Issues: when is this version of multi-class better? Several easy improvements are possible via modifying the loss function. 37

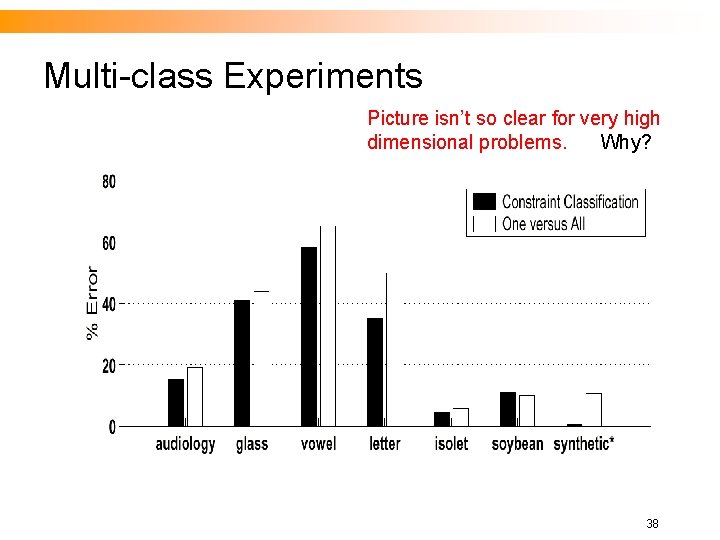
Multi-class Experiments Picture isn’t so clear for very high dimensional problems. Why? 38

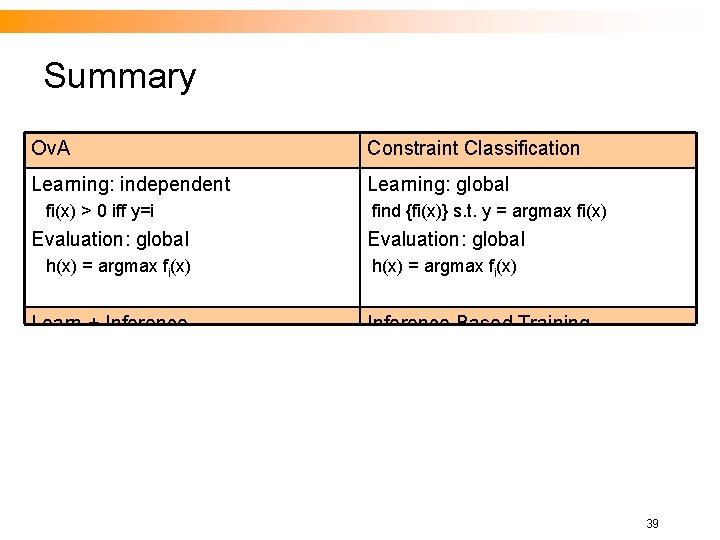
Summary Ov. A Constraint Classification Learning: independent Learning: global fi(x) > 0 iff y=i Evaluation: global h(x) = argmax fi(x) find {fi(x)} s. t. y = argmax fi(x) Evaluation: global h(x) = argmax fi(x) Learn + Inference Based Training Learning: independent Learning: global fi(x) > 0 iff “i is a part of y” Evaluation: global Inf h(x) = argmaxyin. C SU fi(x) find {fi(x)} s. t. y = argmax fi(x) Evaluation: global h(x) = argmax fi(x) 39

Structured Output Learning n Abstract View: ¨ n Decomposition versus Constraint Classification More details: Inference with Classifiers 40

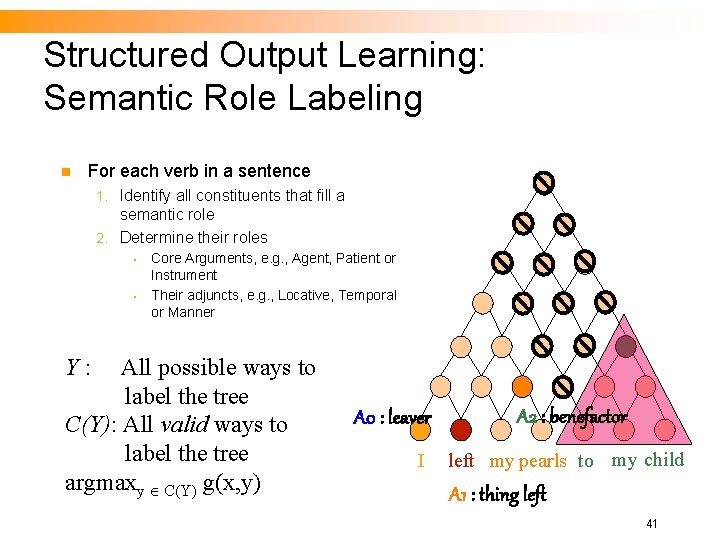
Structured Output Learning: Semantic Role Labeling n For each verb in a sentence Identify all constituents that fill a semantic role 2. Determine their roles 1. • • Core Arguments, e. g. , Agent, Patient or Instrument Their adjuncts, e. g. , Locative, Temporal or Manner Y: All possible ways to label the tree C(Y): All valid ways to label the tree argmaxy C(Y) g(x, y) A 0 : leaver I A 2 : benefactor left my pearls to my child A 1 : thing left 41

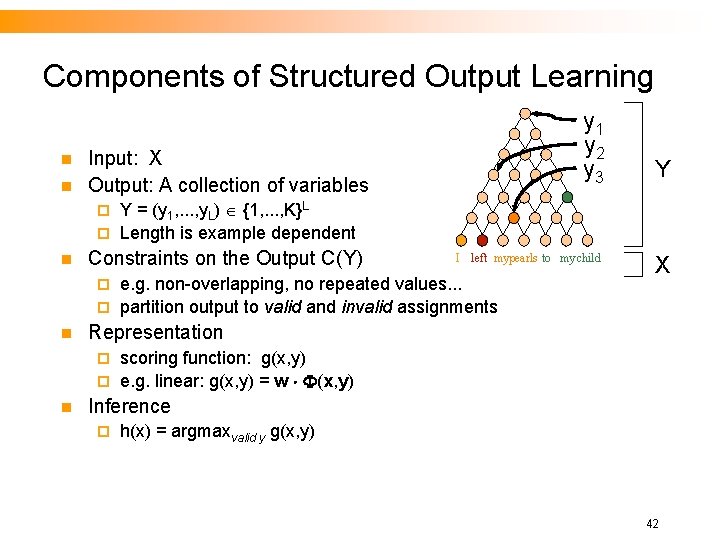
Components of Structured Output Learning n n y 1 y 2 y 3 Input: X Output: A collection of variables Y Y = (y 1, . . . , y. L) {1, . . . , K}L ¨ Length is example dependent ¨ n Constraints on the Output C(Y) I left mypearls to my child e. g. non-overlapping, no repeated values. . . ¨ partition output to valid and invalid assignments ¨ n X Representation scoring function: g(x, y) ¨ e. g. linear: g(x, y) = w (x, y) ¨ n Inference ¨ h(x) = argmaxvalid y g(x, y) 42

Decomposition-based Learning n Many choices for decomposition ¨ n Depends on problem, learning model, computation resources, etc. . . Value-based decomposition ¨ A function for each output value n n ¨ fk(x, l), k = {1, . . , K} e. g. SRL tagging f. A 0(x, node), f. A 1(x, node), . . . Ov. A learning n fk(x, node) > 0 iff k=y 43

Learning Discriminant Functions: The General Setting n n n n g(x, y) > g(x, y’) w (x, y) > w (x, y’) w (x, y, y’) = w ( (x, y) - (x, y’)) > 0 P(x, y) = { (x, y, y’)} y’ Y y P(S) = {P(x, y)}(x, y) S y’ Y y Learn unary classifer over P(S) (binary) (+P(S), -P(S)) Used in many works [C 02, WW 00, CS 01, CM 03, TGK 03] 44

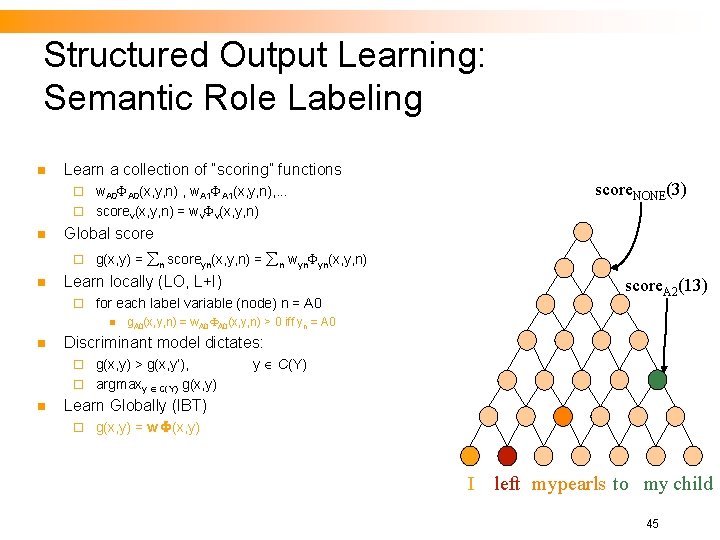
Structured Output Learning: Semantic Role Labeling n Learn a collection of “scoring” functions w. A 0(x, y, n) , w. A 1(x, y, n), . . . ¨ scorev(x, y, n) = wv v(x, y, n) ¨ n Global score ¨ n g(x, y) = n scoreyn(x, y, n) = n wyn yn(x, y, n) Learn locally (LO, L+I) ¨ for each label variable (node) n = A 0 n n score. A 2(13) g. A 0(x, y, n) = w. A 0(x, y, n) > 0 iff yn = A 0 Discriminant model dictates: g(x, y) > g(x, y’), ¨ argmaxy C(Y) g(x, y) ¨ n score. NONE(3) y C(Y) Learn Globally (IBT) ¨ g(x, y) = w (x, y) I left mypearls to my child 45

Multi-class Summary Ov. A Constraint Classification Learning: Independent Learning: global fi(x) > 0 iff y=i Evaluation: global Structured Output h(x) = argmax fi(x) find {fi(x)} s. t. y = argmax fi(x) Evaluation: global h(x) = argmax fi(x) Learn + Inference Based Training Learning: Independent Learning: global fi(x) > 0 iff “i is a part of y” find {fi(x)} s. t. Y = Inference {fi(x)} Evaluation: global Inference Evaluation: global inference h(x) = Inference {fi(x)} Efficient Learning h(x) = Inference {fi(x)} Less Efficent Learning 46