Multi Phase Flow Measurement By S Manickarajan What

Multi Phase Flow Measurement By S. Manickarajan

What is Multi Phase Flow Meter ? v If the measurement fluid consists of more than one phase, the multiphase flow meter comes in present v Examples • Product fluids such as crude oil from wells • Steam and condensate flow

Why Multi Phase Flow Meter is required? v Water breakthrough detection v Gas coning detection v Gas lift optimisation v Other optimisation considerations can be made for chemical injection (e. g. methanol, demulsifier, etc. ) v Custody transfer measurements for production fluid are the basis for money transfer, either between company and government or between two companies.

Water coning or Water breakthrough detection n When a layer of water under the oil layer channeling into the oil accumulation, it is called water breakthrough or water coning phenomena Heterogeneous reservoir without inflow control evidences early water breakthrough.

Gas coning or Gas breakthrough detection n When a part of gas above the oil layer channeling into the oil accumulation, it is called Gas breakthrough or Gas coning phenomena Heterogeneous reservoir without inflow control evidences early gas breakthrough.

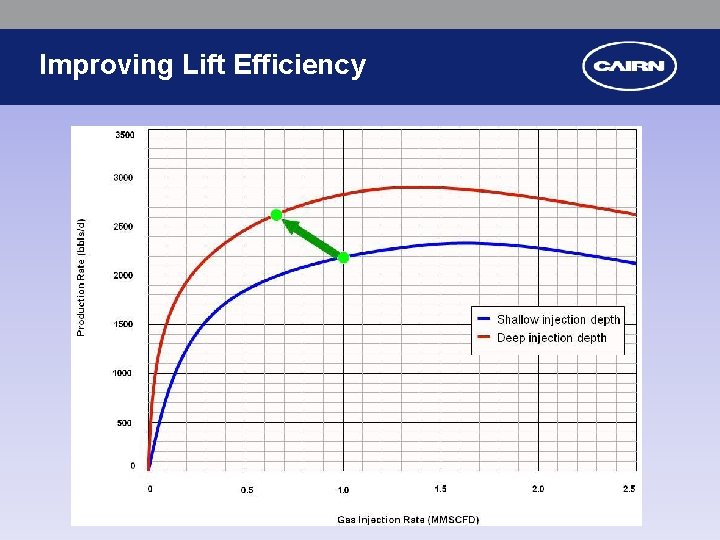
Improving Lift Efficiency

Why Methanol Chemical Injection? v In order to avoid costly downtime due to freeze-ups of deep water well systems , chemicals such as Methanol are injected into each well as a preventive countermeasure. v The methanol Injection shall be decided by observing the water cut profile over a period for early identification of frozen of water

Types of Multi Phase Flow Meter n Separator based MPFM n In line MPFM

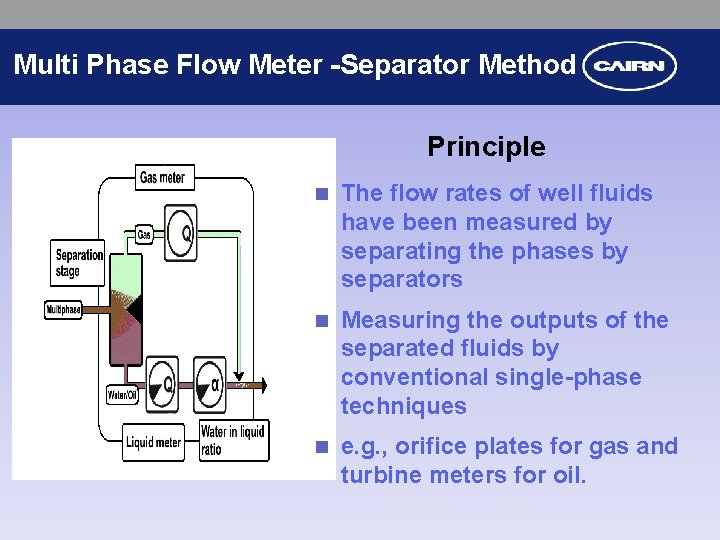
Multi Phase Flow Meter -Separator Method Principle n The flow rates of well fluids have been measured by separating the phases by separators n Measuring the outputs of the separated fluids by conventional single-phase techniques n e. g. , orifice plates for gas and turbine meters for oil.

Multi Phase Flow Meter -Separator Method Constraints n Accuracy depends on separation efficiency Disadvantages n Bulk in Size n High Installation cost

In line MPFM Principle The volumetric flow rate Q =A (α vg + β vw +χ vo) where A is the cross-sectional area of the pipe. Since α + β + χ = 1, only two of the phase fractions (usually gas void fraction α and water fraction β) need to be measured. Q =A {α vg + β vw +[1 - (α + β)] vo } with five independent measurements required to determine the total volumetric Flow rate of the mixture. The mass flow rate M of the three-phase mixture is given by M =A {α vg Dg + β vw Dw +[1 - (α + β)] vo Do } with eight independent measurements required to determine the total mass Flow rate of the mixture.

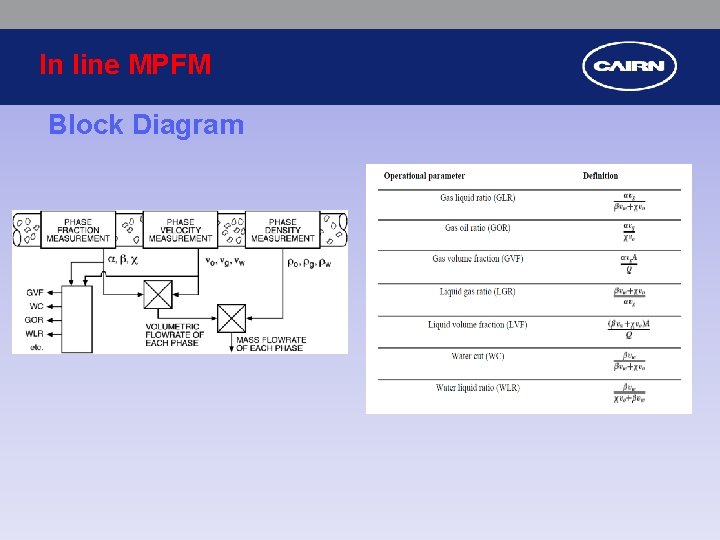
In line MPFM Block Diagram

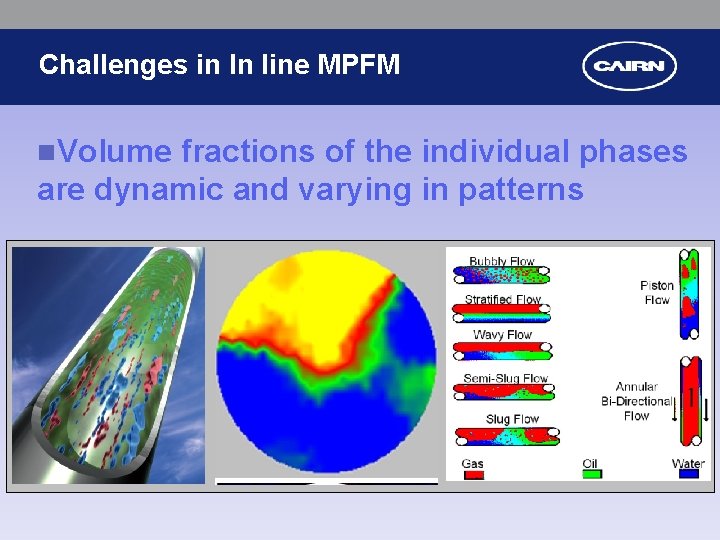
Challenges in In line MPFM n. Volume fractions of the individual phases are dynamic and varying in patterns

Challenges in In line MPFM Significant variation in the PVT properties leads to water at different phases n

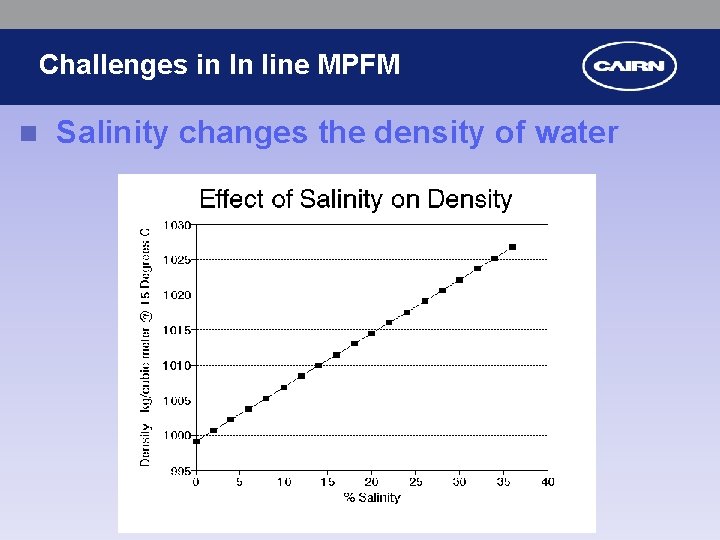
Challenges in In line MPFM n Salinity changes the density of water

Challenges in In line MPFM Velocities of individual phases are different due to different in viscosities n

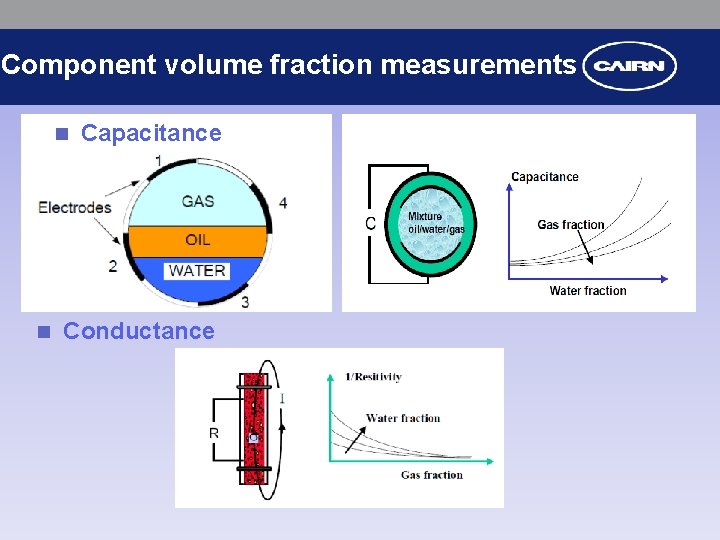
Component volume fraction measurements n n Capacitance Conductance

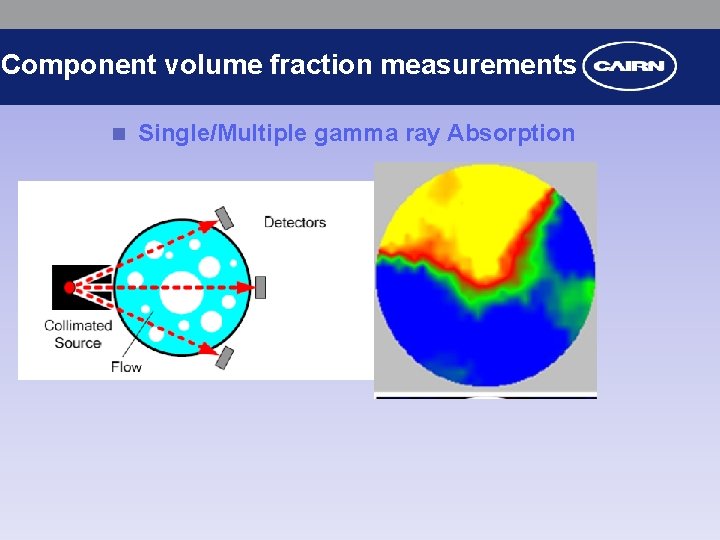
Component volume fraction measurements n Single/Multiple gamma ray Absorption

Component volume fraction measurements n Microwave Propagation

Velocity measurements n Cross correlation techniques n Acoustic attenuation n Coriolis device n Dual Venturi n Positive displacement device

Cross-Correlation Techniques • • Assume that the phases fractions pattern remains unaltered as it travels between the sensors The output signal generated by the downstream sensor will then be a timedelayed replica of the upstream sensor's output.

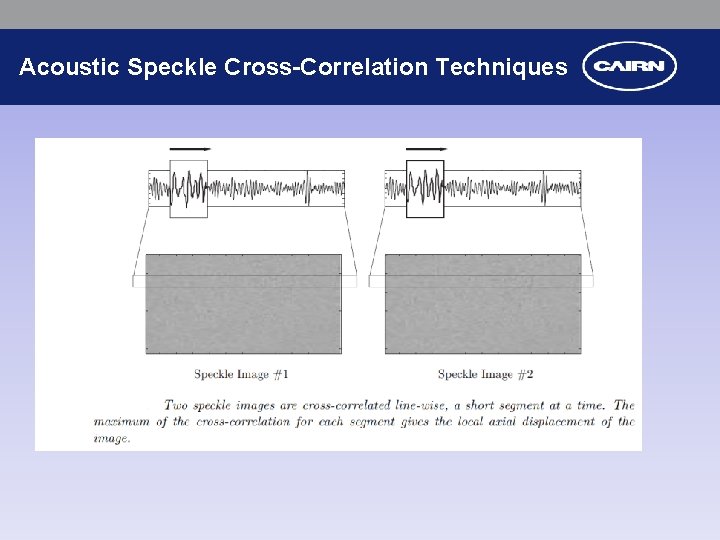
Acoustic Speckle Cross-Correlation Techniques

Principle of Coriolis flow meter for 2 Phase Measurement at MPT - Aishwarya PLR • When an oscillating excitation force is applied to the tube causing it to vibrate; the tube will vibrate at its natural frequency which depends upon the linear density. • With the measurement of the vibrating frequency, density of the fluid stream can be accurately obtained. • The fluid flowing through the tube will induce a rotation or twist which is directly affected by the mass passing through the tube. Hence mass flow rate shall be measured.

Principle of Coriolis flow meter for 2 Phase Measurement at MPT - Aishwarya PLR By conservation of Mass MW + M O Q W X DW + Q O X DO ML = Q L X DL = Where DL is density of total liquid measured by coriolisis meter Do is density of oil to be configured Dw is density of water to be configured Let WC is the water cut, then QL X WC X DW + QL X(1 -WC) X DO = QL X DL QL X WC X DW + QL X DO –WC X QL X DO = Q L X DL WC X DW + DO –WC X DO = DL WC X DW–WC X DO = D L - DO WC X ( DW– DO ) = DL – DO WC = (DL – DO ) / ( DW– DO ) And hence QW = WC X QL Where QL –Total Liquid Volume measured by Coriolisis QO = (1 -WC) QL

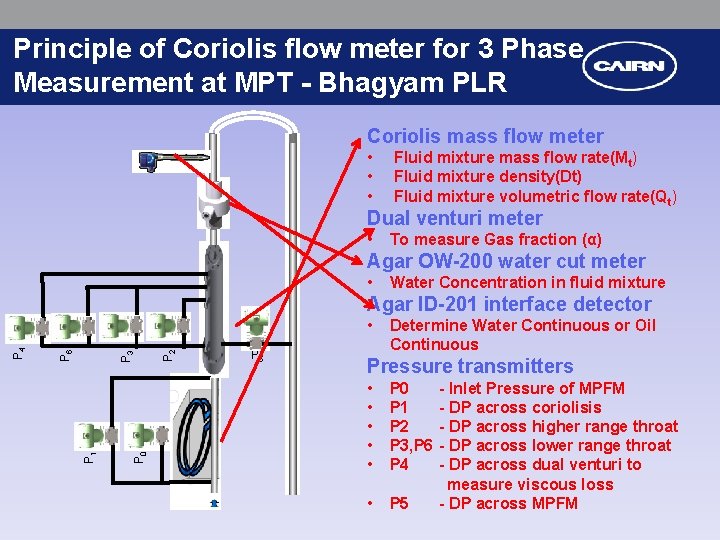
Principle of Coriolis flow meter for 3 Phase Measurement at MPT - Bhagyam PLR Coriolis mass flow meter • • • Fluid mixture mass flow rate(Mt) Fluid mixture density(Dt) Fluid mixture volumetric flow rate(Qt) Dual venturi meter • To measure Gas fraction (α) Agar OW-200 water cut meter • Water Concentration in fluid mixture Agar ID-201 interface detector P 0 P 1 P 2 P 3 P 6 P 4 • P 5 Determine Water Continuous or Oil Continuous Pressure transmitters • • • P 0 P 1 P 2 P 3, P 6 P 4 • P 5 - Inlet Pressure of MPFM - DP across coriolisis - DP across higher range throat - DP across lower range throat - DP across dual venturi to measure viscous loss - DP across MPFM

Principle of Coriolis flow meter for 3 Phase Measurement at MPT - Bhagyam PLR • When an oscillating excitation force is applied to the tube causing it to vibrate; the tube will vibrate at its natural frequency which depends upon the linear density. • With the measurement of the vibrating frequency, density of the fluid stream can be accurately obtained. • The fluid flowing through the tube will induce a rotation or twist which is directly affected by the mass passing through the tube. Hence mass flow rate shall be measured.

Dual venturi meter dp 1 D 1 dp 2 D 2 d 2 • By conservation of Mass M 1=M 2 Applying Bernoulli’s Theorem for Ventury 1&2 • δ 1 dp 1=δ 2 dp 2 • V 1/V 2=δ 1 dp 1/δ 2 dp 2 • V 2/V 1=δ 2 dp 2/δ 1 dp 1 • V 1=Vo 1+Vw 1+Vg 1 and V 2=Vo 2+Vw 2+Vg 2 • At 1 and 2 Water volume will not change since water is assumed as non-compressible • Vw 2=Vw 1 • Vo 2=Vo 1 -(ε)Dp*Vo 1 Where ε is shrinkage factor of oil as gas in the oil is liberated • Vg 2=(Vg 1*Cg* dp)+(δRs*Vo 1) where δRs is the volume of the gas liberated by oil per unit volume and Cg is expansion co-efficient of gas

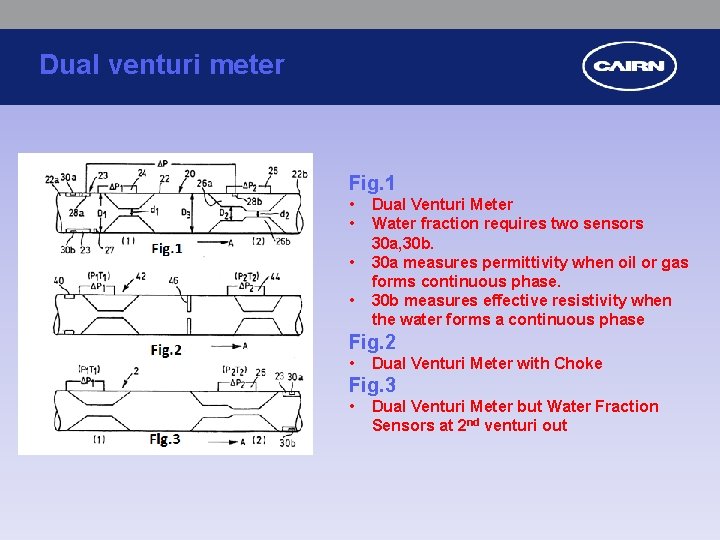
Dual venturi meter Fig. 1 • • Dual Venturi Meter Water fraction requires two sensors 30 a, 30 b. 30 a measures permittivity when oil or gas forms continuous phase. 30 b measures effective resistivity when the water forms a continuous phase Fig. 2 • Dual Venturi Meter with Choke Fig. 3 • Dual Venturi Meter but Water Fraction Sensors at 2 nd venturi out

Component volume fraction measurements n Microwave Propagation

Agar ID-201 interface detector • A radiofrequency signal is provided by the electronic control and radiated by an antenna. • Water in the interface absorbs the radiated energy due to its conductive nature, but hydrocarbon will not. • The amount of absorbed energy is measured by the electronic control and a 4 -20 m. A is generated proportionally to that absorption.

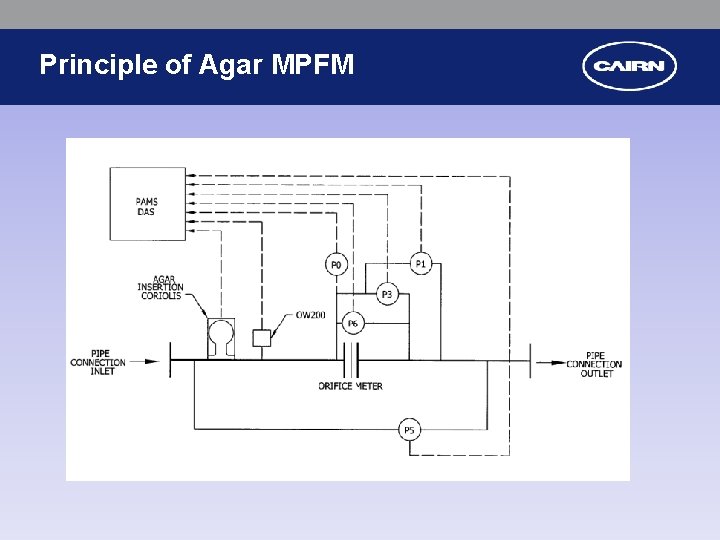
Principle of Agar MPFM

Calculation in Agar MPFM • QT = MT/ DT , Where MT Mass flow rate of Gas and Liquid mixture and DT Density of Gas and Liquid mixture are Measured by Coriolisis Meter By conservation of Mass ML + MG = MT Q L X DL + Q G X DG is density of liquid (Oil & Water) = QTX DT Where DL DG is density of gas (1 - α ) X QT X DL + α X Q T X DG = QTX DT (1 - α ) X QT X DL + α X Q T X DG = Q T X DT (1 - α ) X DL + α X DG = DT D L - α X DL + α X DG = DT α X (DG – DL ) = DT – DL α = (DT – DL ) / ( DG– DL ) By conservation of Mass MW + M O = ML Q W X DW + Q O X DO = QL X DL Where Do is density of oil to be configured Dw is density of water to be configured Let CW is the water cut, then QL X CW X DW + QL X(1 - CW) X DO = QL X DL QL X CW X DW + QL X DO –CWC X QL X DO = Q L X DL QL X CW X DW + QL X DO –CW X QL X DO = Q L X DL CW X DW + DO –CW X DO = DL DL = CW X (DW –DO ) + DO α = (DT– DO – CW X (DW –DO )) / ( DG– DO – CW X (DW –DO )) α = (DT– DO – CW X (DW –DO )) / ( DG– DO ) as CW X (DW –DO ) in Numerator negligible

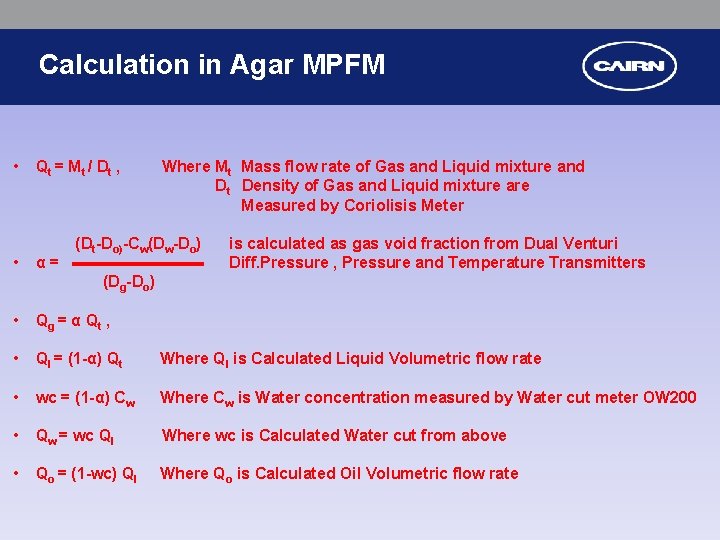
Calculation in Agar MPFM • • Qt = M t / D t , α= Where Mt Mass flow rate of Gas and Liquid mixture and Dt Density of Gas and Liquid mixture are Measured by Coriolisis Meter (Dt-Do)-Cw(Dw-Do) is calculated as gas void fraction from Dual Venturi Diff. Pressure , Pressure and Temperature Transmitters (Dg-Do) • Qg = α Q t , • Ql = (1 -α) Qt Where Ql is Calculated Liquid Volumetric flow rate • wc = (1 -α) Cw Where Cw is Water concentration measured by Water cut meter OW 200 • Qw = wc Ql Where wc is Calculated Water cut from above • Qo = (1 -wc) Ql Where Qo is Calculated Oil Volumetric flow rate

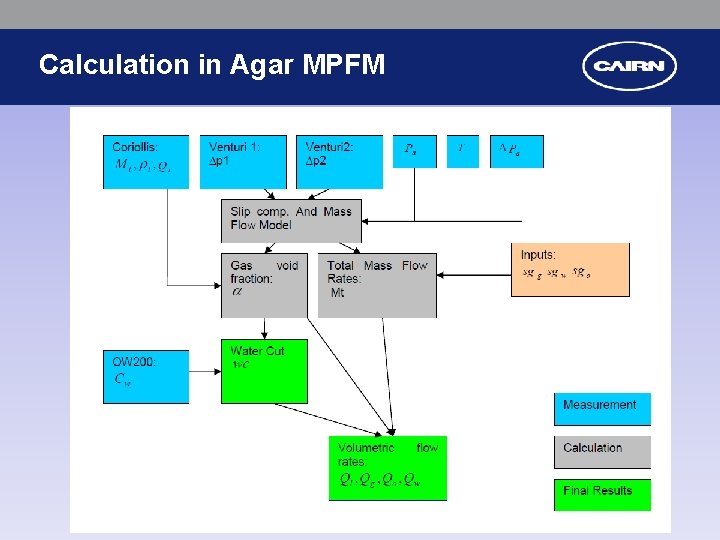
Calculation in Agar MPFM

MPFM installed in Mangala & Aishwarya Make Model Location AGAR MPFM-50 Bhagyam Header Line Schlumberger Phase watcher VX MPT and Aishwarya Wellpads test header Haimo MFM-2100/M-3 MPT Wellpads test header Emerson Model 3700 Aishwarya PLR : :

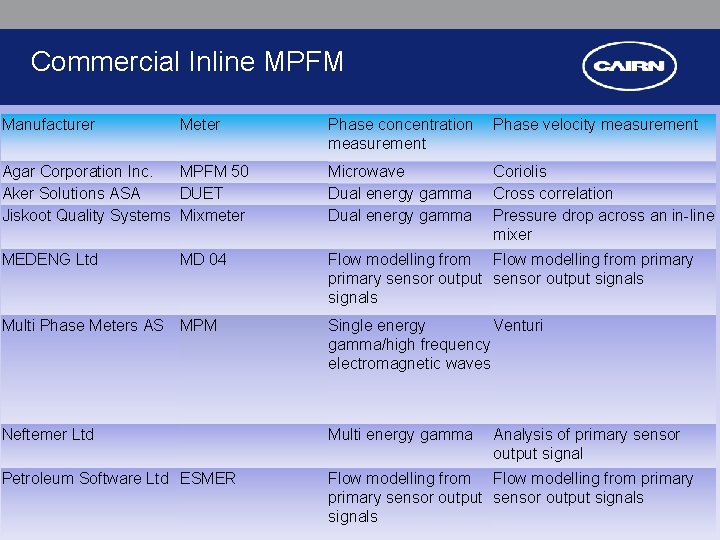
Commercial Inline MPFM Manufacturer Meter Phase concentration Phase velocity measurement Agar Corporation Inc. MPFM 50 Aker Solutions ASA DUET Jiskoot Quality Systems Mixmeter Microwave Dual energy gamma MEDENG Ltd Flow modelling from primary sensor output signals MD 04 Coriolis Cross correlation Pressure drop across an in-line mixer Multi Phase Meters AS MPM Single energy Venturi gamma/high frequency electromagnetic waves Neftemer Ltd Multi energy gamma Petroleum Software Ltd ESMER Analysis of primary sensor output signal Flow modelling from primary sensor output signals

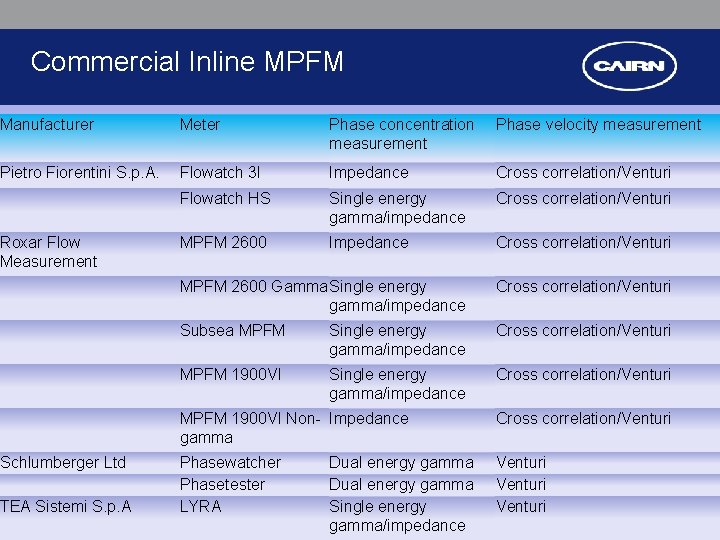
Commercial Inline MPFM Manufacturer Meter Phase concentration measurement Phase velocity measurement Pietro Fiorentini S. p. A. Flowatch 3 I Impedance Cross correlation/Venturi Flowatch HS Single energy gamma/impedance Cross correlation/Venturi Roxar Flow Measurement MPFM 2600 Impedance Cross correlation/Venturi MPFM 2600 Gamma. Single energy gamma/impedance Cross correlation/Venturi Subsea MPFM Single energy gamma/impedance Cross correlation/Venturi MPFM 1900 VI Non- Impedance gamma Cross correlation/Venturi Schlumberger Ltd TEA Sistemi S. p. A Phasewatcher Phasetester LYRA Venturi Dual energy gamma Single energy gamma/impedance

References 1. M. J. Berger, J. H. Hubbel et al. , XCOM Photon Cross Section Database, National Institute of Standards and Technology 2. Hans R E van Maanen, Shell Global Solutions, Measurement of the Liquid Water Flow Rate Using Microwave Sensors in Wet-Gas Meters: Not As Simple As You Might Think, North Sea Flow Measurement Workshop 2008. 3. J. P. Couput, G. Salque, P. Gajan, A. Strzelecki, J. L. Fabre, New Correction Method For Wet Gas Flow Metering Based on Two Phase Flow Modelling: Validation on Industrial Air/Oil/Water Tests at Low And High Pressure, North Sea Flow Measurement Workshop 2007. 4. R. de Leeuw, Liquid Correction of Venturi meter Reading in Wet Gas Flow, North Sea Flow Measurement Workshop 1997 5. M. van Werven, H. R. E. van Maanen Modelling Wet Gas Annular/Dispersed Flow Through a Venturi AICh. E Journal , June 2003, Vol. 409, No. 6 6. A Wee, H Berentsen, V. R. Midttveit, H. Moestue, H. O. Hide, Tomography powered multiphase and wetgas meter providing measurements used for fiscal metering, North Sea Flow Measurement Workshop 2007. 7. Handbook of Multiphase Flow Metering, Rev. 2, March 2005, Tekna 8. MPM Meter Qualification – MPM White Paper No. 4 9. Water Salinity Measurement & Auto Configuration – MPM White Paper No. 2 10. A. Wee, I. M. Skjældal, Ø. L. Bø, Multiphase metering with early detection of changes in water salinity – Americas Workshop, 2009 11. Ø. L. Bø, A. Wee, I. M. Skjældal, Tomography powered 3 -phase flow metering in the wet gas regine, 8 th International South East Hydrocarbon Flow Measurement Workshop, March 2009 12. MPM Droplet Count, MPM White Paper No. 7 13. United States Patent for Dual Venturi Multiphase flow meter.

ANY QUESTIONS?