MTRIXELMOZDULSMDSZER MTRIXARITMETIKAI ALAPFOGALMAK Tartk Statikja II SZCHENYI EGYETEM

MÁTRIX-ELMOZDULÁSMÓDSZER MÁTRIXARITMETIKAI ALAPFOGALMAK Tartók Statikája II. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék 1

A MÁTRIX DEFINÍCIÓJA Lineáris (vagy linearizálható) függvénykapcsolatban álló halmazok vizsgálatára igen alkalmas a lineáris egyenlet(rendszer). Az ebben szereplő együtthatók számtáblázatba rendezve a halmazok diszkrét elemei közötti összefüggéseket tömören és matematikailag korrekt módon írják le. Az ilyen kétdimenziós, diszkrét elemekből álló táblázatot MÁTRIXnak nevezzük. Tartók Statikája II. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék 2

A MÁTRIX DEFINÍCIÓJA Az m × n méretű mátrixnak m sora és n oszlopa van. i= 1, 2, 3, . . . , n j= 1, 2, 3, . . . , m Tartók Statikája II. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék 3

NÉHÁNY EGYSZERŰ NEVEZETES MÁTRIX A sorok és az oszlopok felcserélésével kapott mátrix az eredeti transzponáltja. Tartók Statikája II. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék 4

NÉHÁNY EGYSZERŰ NEVEZETES MÁTRIX Az egydimenziós mátrix neve vektor. Alaphelyzetben a vektor oszlopvektort jelöl, a sorvektort a (neki megfelelő) oszlopvektor transzponáltjaként értelmezzük. Tartók Statikája II. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék 5

NÉHÁNY EGYSZERŰ NEVEZETES MÁTRIX Ha a mátrix sorainak és oszlopainak száma megegyezik, kvadratikus mátrixról beszélünk. A kvadratikus mátrix sorainak ill. oszlopainak száma a mátrix rendje. Tartók Statikája II. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék 6

NÉHÁNY EGYSZERŰ NEVEZETES MÁTRIX Ha a kvadratikus mátrix megegyezik a saját transzponáltjával, szimmetrikus mátrixról beszélünk. Tartók Statikája II. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék 7

NÉHÁNY EGYSZERŰ NEVEZETES MÁTRIX Ha a kvadratikus mátrixnak csak a főátlójában van zérustól különböző elem, a mátrixot diagonális mátrixnak nevezzük. Tartók Statikája II. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék 8

NÉHÁNY EGYSZERŰ NEVEZETES MÁTRIX Ha a diagonális mátrix főátlójában lévő valamennyi elem értéke 1, akkor az egységmátrixot kapjuk (ezzel szorozva a szorzat mátrix az eredeti tényező-mátrixot adja vissza). E=dij Tartók Statikája II. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék 9

NÉHÁNY EGYSZERŰ NEVEZETES MÁTRIX. A kontinuáns mátrix olyan tridiagonális kvadratikus mátrix, amelyben csak a főátlóban, és annak közvetlen szomszédjaiban álló elemek különböznek zérustól. [aij=0, ha |i-j|>1] Tartók Statikája II. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék 10

NÉHÁNY EGYSZERŰ NEVEZETES MÁTRIX Ha a szimmetrikus mátrixban a főátló mellett több szomszéd is zérustól különböző, sávmátrixról, vagy szalagmátrixról beszélünk. [aij=0, ha |i-j|>k, ahol a sávszélesség 2 k] Ha a kvadratikus mátrixban a főátló alatt, vagy a főátló felett csak zérus elemek állnak, háromszögmátrixról beszélünk. [aij=0, ha i<j, ill. aij=0, ha i>j, ] Ha a mátrix minden eleme zérus, a mátrix neve (furcsa és meglepő módon): zérusmátrix. Tartók Statikája II. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék 11

EGYSZERŰ MÁTRIXMŰVELETEK ÖSSZEADÁS-KIVONÁS: a műveleteket rendre a megfelelő elemeken kell végrehajtani! Csak azonos méretű mátrixok vonhatók össze! A±B=C [aij] ± [ bij ] = [ cij] MÁTRIX SZORZÁSA KONSTANSSAL: a konstanssal minden elem külön-külön szorzandó. k×D = [k×dij] Tartók Statikája II. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék 12

EGYSZERŰ MÁTRIXMŰVELETEK KÉT MÁTRIX SZORZATA A mátrix-szorzásban a tényezők NEM felcserélhetők! A szorzás csak akkor értelmezhető, ha az első tényező OSZLOPAINAK és a második tényező SORAINAK száma MEGEGYEZIK. Ilyenkor a szorzatmátrix ij indexű eleme az első tényező i-ik sorának (mint sorvektornak) és a második tényező j-ik oszlopának (mint oszlopvektornak) a SKALÁRIS SZORZATA. r ckl=S(a ×b ) kj jl j=1 A × B = C (m, r) (r, n) (m, n) Tartók Statikája II. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék 13

EGYSZERŰ MÁTRIXMŰVELETEK SOR- ÉS OSZLOPVEKTOR SZORZATA Egy sor- és egy oszlopvektor akkor szorozható össze, ha elemszámuk megegyezik. Ilyenkor (skalár)szorzatuk eredménye egy SZÁM. a. T (1, n) n ×(n, 1) b =(1, 1) c ahol c = i=1 S (ai×bi) c Tartók Statikája II. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék 14

EGYSZERŰ MÁTRIXMŰVELETEK OSZLOP- ÉS SORVEKTOR SZORZATA Egy oszlop- és egy sorvektor mindenképp összeszorozható, a szorzat egy MÁTRIX, amelyben a sorok száma az első tényező elemszámával, az oszlopok száma a második tényező elemszámával egyezik meg. Az így előálló mátrixok neve DIÁD. T = C ahol c = a ×b a × b i, j i j (m, 1) (1, n) (m, n) Minden mátrix felírható diádok összegeként. A mátrixot előállító minimális diádszám a mátrix rangja, r(A). A rang a mátrix lineárisan független sorainak ill. oszlopainak számával (is) megegyezik, tehát a sor- ill. oszlopszámnál nagyobb nem lehet. Tartók Statikája II. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék 15

NEVEZETES MÁTRIXOK Ha egy kvadratikus mátrix rendje és rangja azonos, a mátrix nemszinguláris (determinánsa nem zérus). Ha a mátrix nem kvadratikus, vagy rangja kisebb a rendjénél (ez esetben determinánsa zérus), a mátrix szinguláris. A nemszinguláris mátrixok esetében létezik az inverzmátrix, amelynek az eredeti mátrixszal képzett szorzata az egységmátrix: Tartók Statikája II. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék 16

NEVEZETES MÁTRIXOK A (kvadratikus) mátrix ortogonális, ha inverze és transzponáltja azonos. Az ortogonális mátrixokra igaz, hogy: Tartók Statikája II. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék 17

A DERÉKSZÖGŰ KOORDINÁTARENDSZER MÁTRIXELMÉLETI ALAPJAI A pontok helyét, a vektorok állását a térben a koordinátageometria eszközrendszerével kezeljük. Leggyakrabban a Descartes-féle derékszögű (ortogonális) koordinátarendszert alkalmazzuk. Ilyenkor egy pont helyét a tengelyekkel párhuzamos (egység)vektorok, és egy-egy, az illető tengely mentén mérendő távolságot mérő skalárszám szorzata adja a megfelelő koordinátát. A fenti ábrázolás alapját a koordinátatengely-irányú (egység)vektorok képezik, ezért ezeket a rendszer bázisvektorainak nevezzük. Tartók Statikája II. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék 18

A DERÉKSZÖGŰ KOORDINÁTARENDSZER MÁTRIXELMÉLETI ALAPJAI Ortogonális (bázis) vektorrendszert alkot az az n darab, n méretű, nemzérus vektor, amelyekre igaz, hogy páronként skalárszorzatuk zérus. Ha emellett a (bázis)vektorok mindegyikére igaz, hogy a saját magával képzett skalárszorzata 1, akkor ortonormált (bázis)vektorrendszerről beszélhetünk. ha j≠k; ha j=k Ezek felhasználásával az n dimenziós (matematikai) „tér”-ben egyértelműen megadható egy pont helyzete, egy vektor állása. Tartók Statikája II. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék 19

A DERÉKSZÖGŰ KOORDINÁTARENDSZER MÁTRIXELMÉLETI ALAPJAI Az egymásra kölcsönösen merőleges (egység)vektorokból álló mátrix mindig ortogonális. Az (n méretű) egységmátrixból egy (bármelyik) egységvektorral képzett diádot levonva annak rangja eggyel csökken. Az olyan mátrixot, vektort, amelynek elemei maguk is mátrixok, ill. vektorok, hipermátrixnak, ill. hipervektornak nevezzük. Tartók Statikája II. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék 20

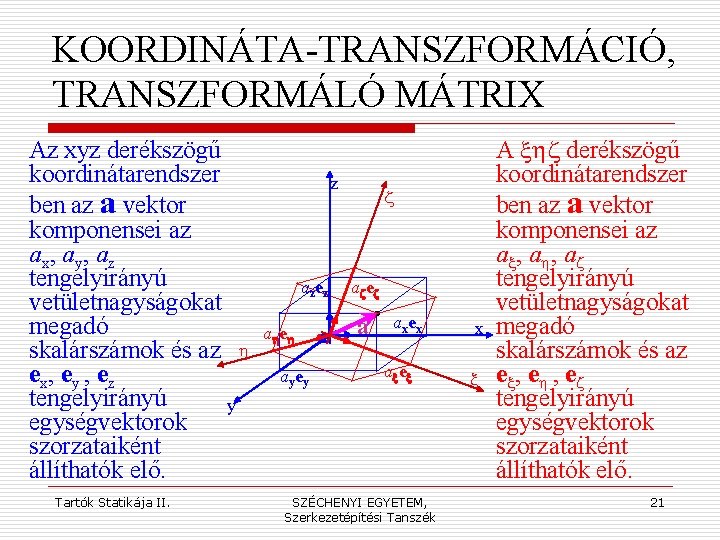
KOORDINÁTA-TRANSZFORMÁCIÓ, TRANSZFORMÁLÓ MÁTRIX Az xyz derékszögű koordinátarendszer ben az a vektor komponensei az ax, ay, az tengelyirányú vetületnagyságokat megadó skalárszámok és az h e x, e y , e z tengelyirányú y egységvektorok szorzataiként állíthatók elő. Tartók Statikája II. z azez aheh ayey z azez a axex SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék x x A xhz derékszögű koordinátarendszer ben az a vektor komponensei az ax, ah, az tengelyirányú vetületnagyságokat megadó skalárszámok és az e x, e h , e z tengelyirányú egységvektorok szorzataiként állíthatók elő. 21

KOORDINÁTA-TRANSZFORMÁCIÓ, TRANSZFORMÁLÓ MÁTRIX A vetületek skalárszámait (oszlop)vektorba rendezve az a vektor a tengelyirányú egységvektorokból képzett sorvektor és a vetületnagyságokból képzett oszlopvektor skaláris szorzataként jelenik meg. Természetesen a kétféle koordinátarendszerből előállított a vektor nem különbözhet, azaz: Tartók Statikája II. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék 22

KOORDINÁTA-TRANSZFORMÁCIÓ, TRANSZFORMÁLÓ MÁTRIX Ha az előbbi egyenlőség mindkét oldalát balról megszorozzuk az ex-ey-ez egységvektorokból képzett (a sorvektor transzponáltjaként értelmezhető) oszlopvektorral, a bal oldalon (az egységvektorok ortonormáltsága miatt) az egységmátrix, a jobb oldalon a transzformációs mátrix lesz az a vetületvektor szorzója. (Ez a transzformáció a xhz koordinátarendszerből az xyz-be visz át. ) Tartók Statikája II. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék 23

KOORDINÁTA-TRANSZFORMÁCIÓ, TRANSZFORMÁLÓ MÁTRIX A T transzformációs (vagy: forgató-) mátrix elemei az xyz ill. a xhz koordinátarendszerek tengelyirányú egységvektorainak skaláris szorzatai, amik valójában (a vektorok normáltsága miatt) a megfelelő tengelyek által bezárt szögek koszinuszai. Ha a forgatás csak egy síkban történik (pl. a z tengely körül), akkor a T transzformációs (vagy: forgató-) mátrix egyszerűbb alakba írható: Tartók Statikája II. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék 24

MÁTRIX-ELMOZDULÁSMÓDSZER A FELTÉTELI MÁTRIXEGYENLET(RENDSZER) Tartók Statikája II. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék 25

AZ ELMOZDULÁSMÓDSZER MÁTRIXEGYENLETE Ax+a 0=0 Kv=q v=x, q=a 0, K=-A Tartók Statikája II. az elmozdulásmódszer klasszikus feltételi egyenlete a mátrix-elmozdulásmódszer és a klasszikus elmozdulásmódszer jelöléseinek megfeleltetése: v a csomóponti elmozdulások vektora q a csomópontokra ható erők-nyomatékok vektora K a szerkezet merevségi mátrixa SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék 26

MÁTRIX-ELMOZDULÁSMÓDSZER A CSOMÓPONTI DINÁMOKELMOZDULÁSOK Tartók Statikája II. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék 27

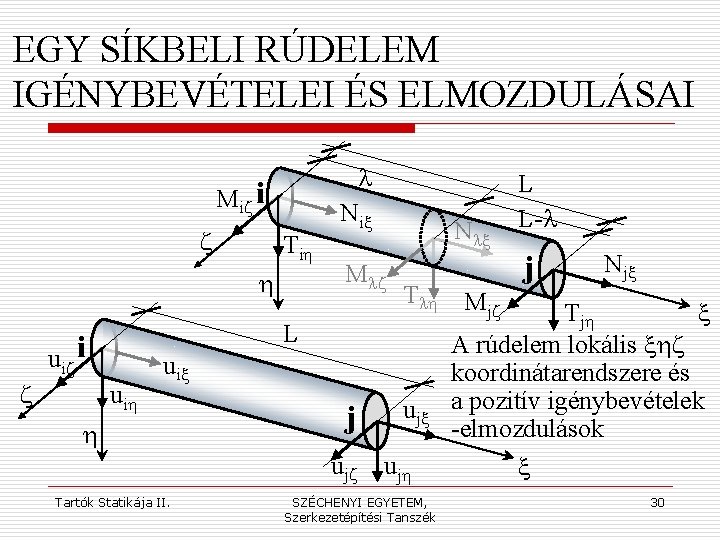
AZ ALKALMAZOTT KOORDINÁTARENDSZEREK A szerkezet vizsgálata során kétféle koordinátarendszert célszerű használni: o o a csomópontok adatait és jellemzőit (csomóponti erőknyomatékok, csomóponti eltolódások-elfordulások) a szerkezet xyz globális koordinátarendszerében lehet jól kezelni; a rúdelemek adatait és jellemzőit (belső erő- és nyomatéki függvények, keresztmetszeti elmozdulási és alakváltozási függvények) a rúdelem saját, rudanként felvett xhz lokális koordinátarendszerében lehet jól kezelni. Tartók Statikája II. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék 28

A CSOMÓPONTI DINÁMOKELMOZDULÁSOK JELÖLÉSE Általános (térbeli) esetben a csomópontra működő erőhatások és a csomópont elmozdulásai (a csomópont elmozdulási szabadságfokának megfelelően) hatfélék lesznek: Fix, Fiy, Fiz, Mix, Miy, Miz, ill. eix, eiy, eiz, fix, fiy, fiz Síkbeli (pl. xy síkbeli) szerkezet esetében a csomóponti erőkelmozdulások a következők: Fix, Fiy, Miz, ill. eix, eiy, fiz Ezek az erő- ill. elmozdulás-összetevők (oszlop)vektor(ok)ba rendezhetők, és ezekből a csomópontonkénti „vektor-blokkok”ból áll össze a teljes szerkezet erő- ill. elmozdulásvektora. Tartók Statikája II. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék 29

EGY SÍKBELI RÚDELEM IGÉNYBEVÉTELEI ÉS ELMOZDULÁSAI Miz i z Tih h z l Nix Mlz L uiz i uih Nlx Tlh M jz uix h j ujz Tartók Statikája II. ujx ujh SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék L L-l j Njx Tjh x A rúdelem lokális xhz koordinátarendszere és a pozitív igénybevételek -elmozdulások x 30

A RÚDERŐK ÉS A CSOMÓPONTI ERŐK MEGFELELTETÉSE Az i-j jelű rúdon (i<j) a rúd igénybevételeiként (sij, j) a nagyobbik sorszámú (j jelű) végen számítható belső erőket definiáljuk. Ezek megegyeznek a rúd j végére ható külső erőkkel (sj=sij, j). A kisebbik sorszámú (i jelű) végen működő külső erők az ott értelmezett igénybevételek ellentettjeivel egyeznek meg (si=-sij, i). A rúd saját (statikai és kinematikai) terhelését külön kezeljük. Tartók Statikája II. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék 31

A CSOMÓPONTI ERŐK A csomópontokra ható erők a következők lehetnek: o o o közvetlen csomóponti erő közvetlen csomóponti nyomaték a rúdról (rudakról) a csomópontra átadódó erő (ez származhat a rúd erőterheléséből, a rúd kinematikai terheléséből) o a rúdról (rudakról) a csomópontra átadódó nyomaték (ez származhat a rúd erőterheléséből, a rúd kinematikai terheléséből) Tartók Statikája II. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék 32

MÁTRIX-ELMOZDULÁSMÓDSZER A SZERKEZET MEREVSÉGI MÁTRIXA Tartók Statikája II. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék 33

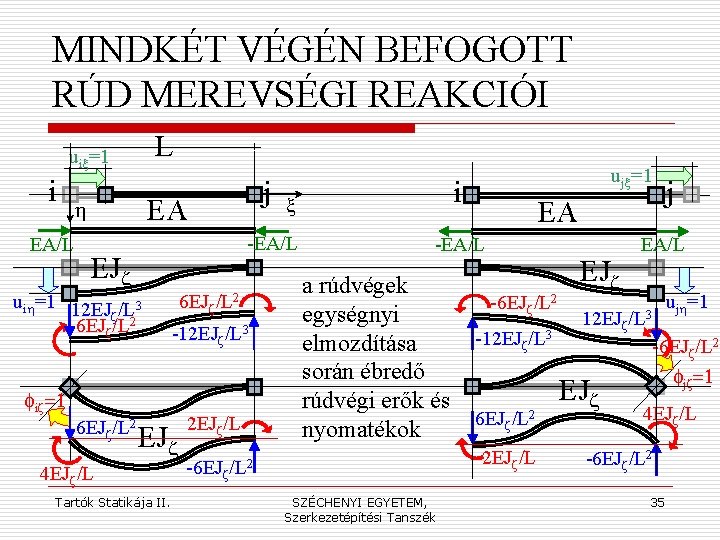
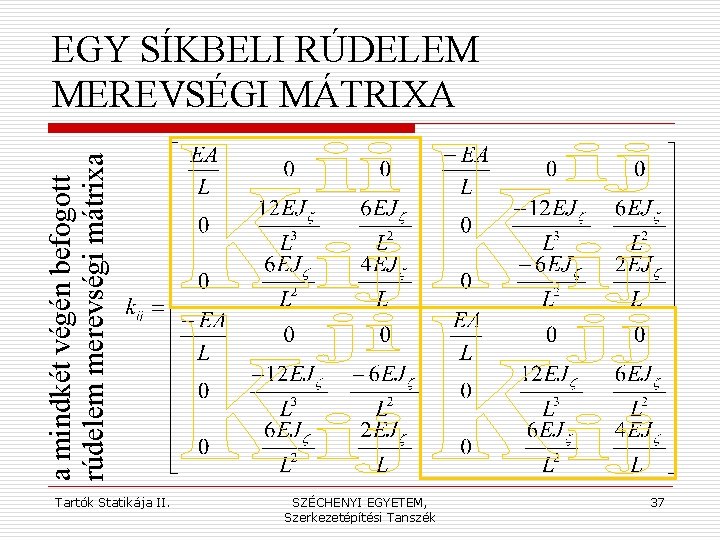
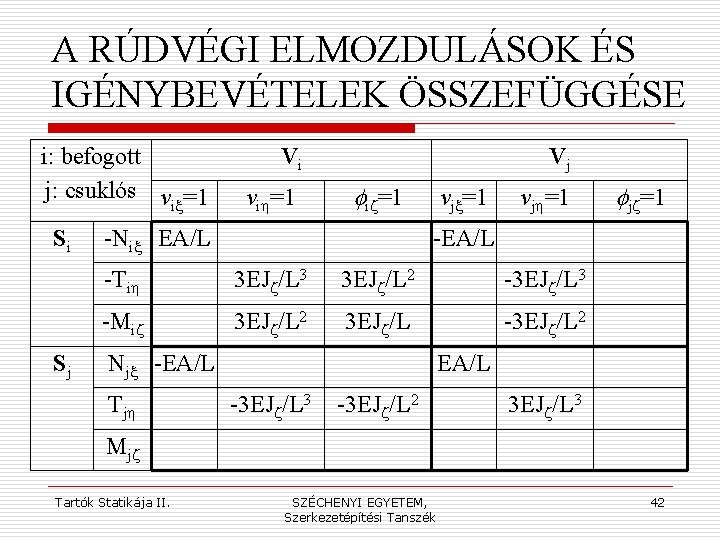
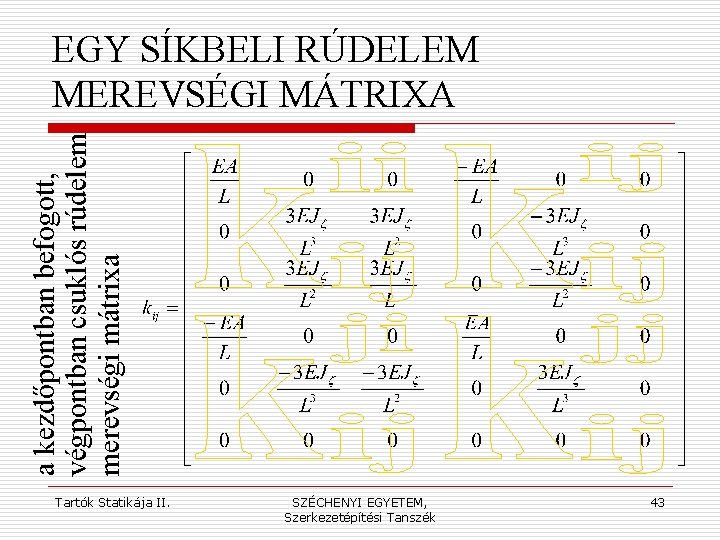
A MEREVSÉGI MÁTRIX DEFINÍCIÓJA A szerkezet(i elem) merevsége mindig egy elmozdulás-elmozdítás nyomán keletkező (belső) erőt, igénybevételt jelent (úgy is értelmezhetjük, hogy a szerkezet ellenállása az elmozdítással szemben). Minthogy az elmozdulás-módszerben a csomóponti elmozdulás-összetevőket tekintjük ismeretleneknek, a síkbeli rúdelem merevségi mátrixa a két rúdvégen beiktatható három-három elmozdulás-komponensből ébred(het)ő három belső dinámot szolgáltatja, azaz egy 6× 6 méretű mátrix. Ez egyúttal jelzi a mátrix struktúráját is: a négy 3× 3 -as méretű blokk az egyes rúdvégeken ébredő erőket adja meg, a saját ill. a másik vég lehetséges elmozdulásai hatására. Tartók Statikája II. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék 34

MINDKÉT VÉGÉN BEFOGOTT RÚD MEREVSÉGI REAKCIÓI L uix=1 i EA h EA/L j EJz uih=1 12 EJ /L 3 z 6 EJz/L 2 -12 EJz/L 3 fiz=1 6 EJz/L 2 EJz 4 EJz/L Tartók Statikája II. 2 EJz/L i x -EA/L ujx=1 EA -EA/L a rúdvégek egységnyi elmozdítása során ébredő rúdvégi erők és nyomatékok -6 EJz/L 2 -12 EJz/L 3 6 EJz/L 2 2 EJz/L -6 EJz/L 2 SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék EJz j EA/L 12 EJz/L 3 ujh=1 -6 EJz/L 2 EJz fjz=1 4 EJz/L -6 EJz/L 2 35

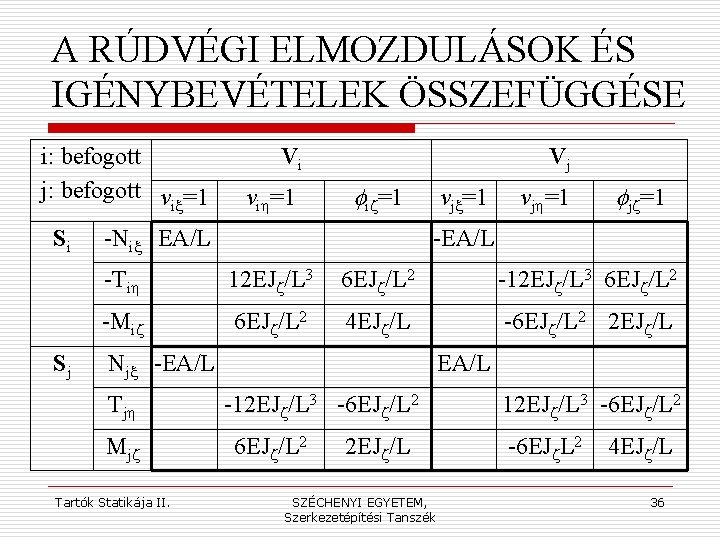
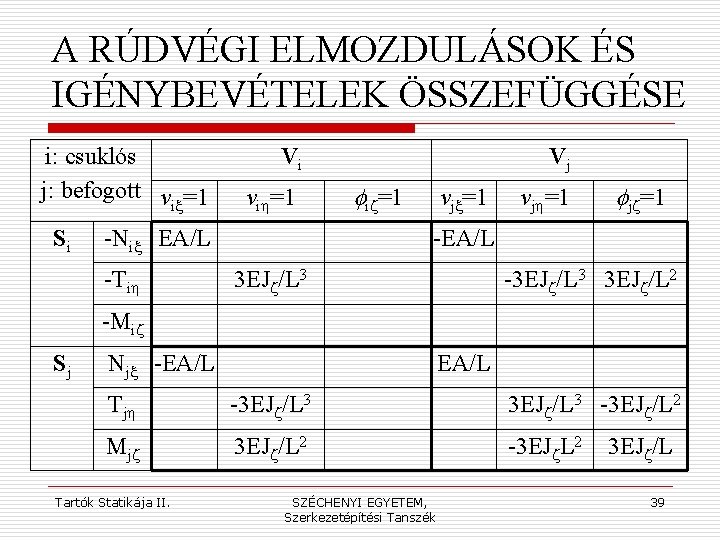
A RÚDVÉGI ELMOZDULÁSOK ÉS IGÉNYBEVÉTELEK ÖSSZEFÜGGÉSE i: befogott j: befogott v =1 ix Si Sj Vi vih=1 Vj fiz=1 -Nix EA/L vjx=1 vjh=1 fjz=1 -EA/L -Tih 12 EJz/L 3 6 EJz/L 2 -Miz 6 EJz/L 2 4 EJz/L -6 EJz/L 2 2 EJz/L Njx -EA/L Tjh Mjz Tartók Statikája II. EA/L -12 EJz/L 3 -6 EJz/L 2 2 EJz/L SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék 12 EJz/L 3 -6 EJz/L 2 -6 EJz. L 2 4 EJz/L 36

a mindkét végén befogott rúdelem merevségi mátrixa EGY SÍKBELI RÚDELEM MEREVSÉGI MÁTRIXA Tartók Statikája II. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék 37

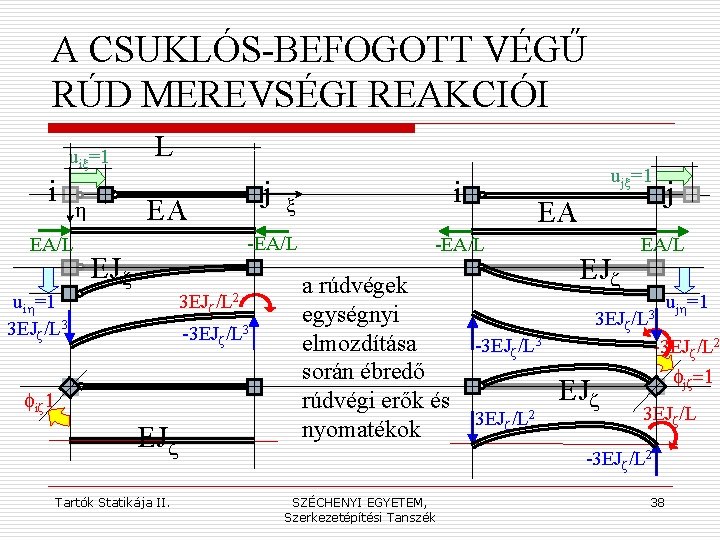
A CSUKLÓS-BEFOGOTT VÉGŰ RÚD MEREVSÉGI REAKCIÓI uix=1 i j EA h EA/L L EJz uih=1 3 EJz/L 3 3 EJz/L 2 -3 EJz/L 3 fiz 1 EJz Tartók Statikája II. i x -EA/L ujx=1 EA -EA/L a rúdvégek egységnyi elmozdítása során ébredő rúdvégi erők és nyomatékok j EJz EA/L 3 EJz/L 3 -3 EJz/L 3 3 EJz/L 2 -3 EJz/L 2 EJz fjz=1 3 EJz/L -3 EJz/L 2 SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék ujh=1 38

A RÚDVÉGI ELMOZDULÁSOK ÉS IGÉNYBEVÉTELEK ÖSSZEFÜGGÉSE i: csuklós j: befogott v =1 ix Si Vi vih=1 -Nix EA/L -Tih Vj fiz=1 vjx=1 vjh=1 fjz=1 -EA/L -3 EJz/L 3 3 EJz/L 2 3 EJz/L 3 -Miz Sj Njx -EA/L Tjh -3 EJz/L 3 -3 EJz/L 2 Mjz 3 EJz/L 2 -3 EJz. L 2 Tartók Statikája II. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék 3 EJz/L 39

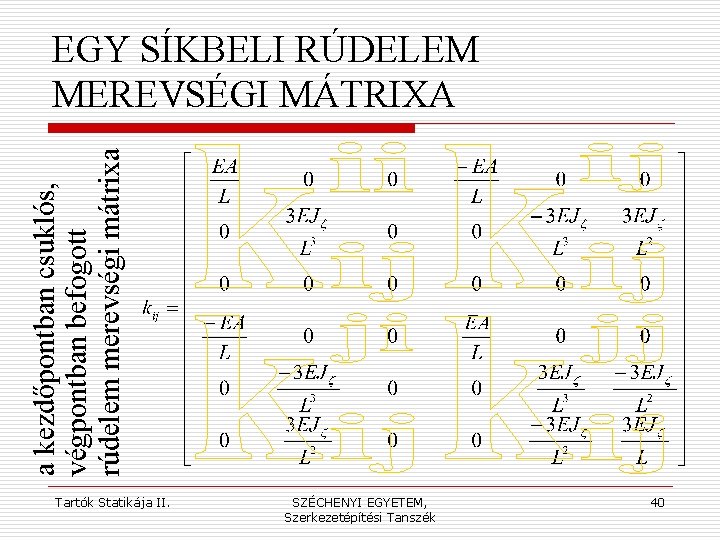
a kezdőpontban csuklós, végpontban befogott rúdelem merevségi mátrixa EGY SÍKBELI RÚDELEM MEREVSÉGI MÁTRIXA Tartók Statikája II. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék 40

A BEFOGOTT-CSUKLÓS VÉGŰ RÚD MEREVSÉGI REAKCIÓI uix=1 i j EA h EA/L L -EA/L EJz uih=1 3 EJz/L 2 3 EJz/L 3 -3 EJz/L 3 fiz 1 3 EJz/L 2 3 EJz/L EJz Tartók Statikája II. -3 EJz/L 2 i x -EA/L ujx=1 EA j EA/L EJz a rúdvégek -3 EJz/L 2 ujh=1 3 egységnyi 3 EJz/L -3 EJz/L 3 elmozdítása során ébredő fjz=1 rúdvégi erők és EJ z nyomatékok SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék 41

A RÚDVÉGI ELMOZDULÁSOK ÉS IGÉNYBEVÉTELEK ÖSSZEFÜGGÉSE i: befogott j: csuklós v =1 ix Si Sj Vi vih=1 Vj fiz=1 -Nix EA/L vjx=1 vjh=1 -EA/L -Tih 3 EJz/L 3 3 EJz/L 2 -3 EJz/L 3 -Miz 3 EJz/L 2 3 EJz/L -3 EJz/L 2 Njx -EA/L Tjh fjz=1 EA/L -3 EJz/L 3 -3 EJz/L 2 3 EJz/L 3 Mjz Tartók Statikája II. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék 42

a kezdőpontban befogott, végpontban csuklós rúdelem merevségi mátrixa EGY SÍKBELI RÚDELEM MEREVSÉGI MÁTRIXA Tartók Statikája II. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék 43

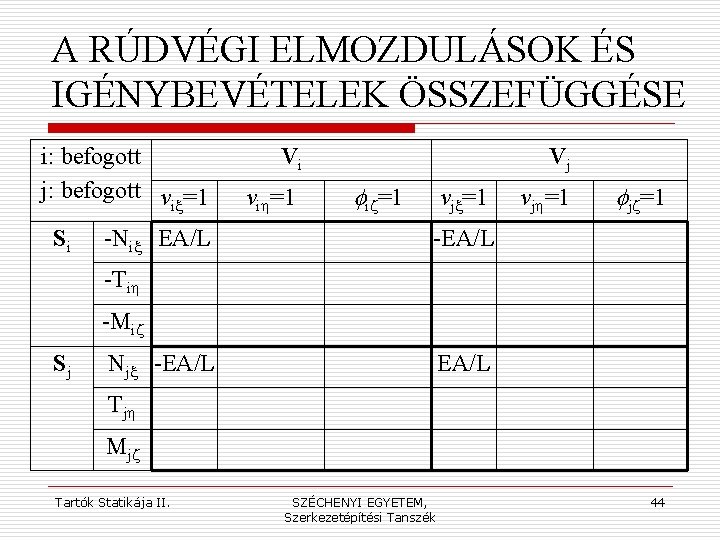
A RÚDVÉGI ELMOZDULÁSOK ÉS IGÉNYBEVÉTELEK ÖSSZEFÜGGÉSE i: befogott j: befogott v =1 ix Si -Nix EA/L Vi vih=1 Vj fiz=1 vjx=1 vjh=1 fjz=1 -EA/L -Tih -Miz Sj Njx -EA/L Tjh Mjz Tartók Statikája II. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék 44

a mindkét végén csuklós rúdelem merevségi mátrixa EGY SÍKBELI RÚDELEM MEREVSÉGI MÁTRIXA Tartók Statikája II. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék 45

A SZERKEZET MEREVSÉGI MÁTRIXA A rúdelem merevségi (hiper)mátrixa (amit a rúdvégi elmozdítások és erők szerint négy al-mátrixból (blokkból) állítottunk össze) a rúd saját, lokális koordinátarendszerében készült. A csomópontok egyensúlyi vizsgálatát viszont csak a globális koordinátarendszerben végezhetjük el. Ehhez a rúd a saját rendszerben készült merevségi mátrixot transzformálni kell, mégpedig kétszeresen: o a valóságos csomóponti elmoz- o a rúdvégek elmozdulásaiból szárdulások (az ezekből ébredő erő- mazó erők viszont a lokális rendket neveztük merevségeknek) szerben értelmezettek, ugyanakglobális irányúak, tehát a rúd sa- kor a csomópontok egyensúlyáját, lokális rendszerében ezeknek hoz a rudakról a csomópontokra csak a megfelelő vetülete fejt ki ható globális irányú erőkompoelmozdító hatást; nensekre van szükségünk. Tartók Statikája II. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék 46

A SZERKEZET MEREVSÉGI MÁTRIXA Az egy rúdelemre érvényes globális koordinátákon értelmezett merevségi mátrix (a lokális koordinátákon előállított merevségi mátrixhoz hasonlóan) négy blokkból áll, amelyek az i-j rúdvégek elmozdulásaiból az i-j rúdvégeken ébredő, most már globális irányú, tehát a többi rúdról adódó erőkkel skalárisan összevonható erőket adják meg. A blokkok felső indexelése a „hely-ok” konvenciót tükrözi. Tartók Statikája II. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék 47

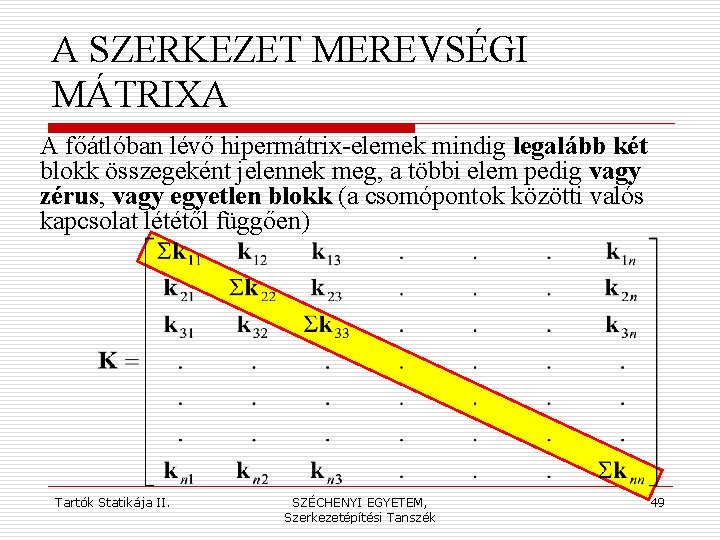
A SZERKEZET MEREVSÉGI MÁTRIXA A globális koordinátarendszerben rudanként értelmezett merevségimátrix blokkokból állíthatjuk elő a teljes szerkezet merevségi mátrixát, amelynek elemei (ill. blokkjai) az oszlopokhoz tartozó egységnyi elmozdulások (csomóponti elmozdulás-csoportok) hatására ébredő csomóponti válasz-dinámokat (dinámcsoportokat) jelenítik meg. A főátlóban a hely és az ok azonos, tehát itt a csomópontba befutó rudak számával megegyező számú rudankénti (globális koordináta irányú) merevségi-mátrix blokk összege adja a teljes merevségi mátrix elemet (blokkot). A többi (hiper)mátrixelem esetében a hely és az ok nem azonos, tehát a vizsgált helyen (csomópontban) ébredő hatás egy másik csomóponti elmozdulás okán keletkezik. Minthogy azonban két pont között csak egy rúd helyezkedhet el, ezek az elemek zéruselemek (ha az illető pontpár között nincs rúd), vagy egyetlen blokkból állnak (ha az illető pontpár között van rúd). Tartók Statikája II. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék 48

A SZERKEZET MEREVSÉGI MÁTRIXA A főátlóban lévő hipermátrix-elemek mindig legalább két blokk összegeként jelennek meg, a többi elem pedig vagy zérus, vagy egyetlen blokk (a csomópontok közötti valós kapcsolat lététől függően) Tartók Statikája II. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék 49

A SZERKEZET MEREVSÉGI MÁTRIXA A szerkezet előbbiekben bemutatott teljes merevségi hipermátrixában egy elem a rudanként előállított és a globális koordinátarendszerbe transzformált merevségi mátrix egy-egy blokkja (vagy blokk-összege), azaz mérete síkbeli tartó esetén 3× 3, térbeli szerkezet esetén 6× 6. A teljes szerkezet merevségi mátrixának mérete (rendje) tehát az elmozdulóképes csomópontok számának és a blokk elemszámának szorzataként állítható elő. (Természetesen a fenti számítás során nem tekintettük a rúdelemeket nyújthatatlannak, de a nyírási deformáció figyelembevételétől eltekintettünk. ) Tartók Statikája II. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék 50

A MEGOLDÁSVEKTOR ELŐÁLLÍTÁSA Az elmozdulásmentesnek feltételezett csomópontokra összegzett erők és nyomatékok szolgáltatják a csomóponti kiegyensúlyozatlan dinámok vektorát, azaz a tehervektort. o A csomópontok egységnyi elmozdulásaira adott szerkezeti válaszok alapján előállított merevségi mátrix adja az együtthatómátrixot. o Ezek ismeretében a mátrixegyenlet felírható és (megfelelő matematikai segédapparátus felhasználásával meg is oldható. o A megoldásvektor elemei az egyensúlyi állapothoz tartozó csomóponti elmozdulás-összetevők lesznek. o Tartók Statikája II. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék 51

A RÚDIGÉNYBEVÉTELEK ELŐÁLLÍTÁSA A csomóponti elmozdulás-összetevők ismeretében a rudak egyedi merevségi mátrixai segítségével meghatározhatók a rúdvégi erők-nyomatékok, és az ezeknek megfelelő igénybevételi függvények. Ezekhez hozzáadva a rúd saját erő- és kinematikai terheléséből adódó igénybevételeket megkapjuk a rúdelemnek, mint a határozatlan tartó egy szerkezeti elemének igénybevételi függvényeit. Tartók Statikája II. SZÉCHENYI EGYETEM, Szerkezetépítési Tanszék 52