MTODOS ESTATSTICOS E NUMRICOS UNIDADE 2 MEDIDAS DE

MÉTODOS ESTATÍSTICOS E NUMÉRICOS UNIDADE 2 MEDIDAS DE CENTRALIZACIÓN E POSICIÓN ÍNDICE IES Isidro Parga Pondal. Departamento de matemáticas

Conceptos 1. Parámetros de centralización: media, mediana e moda. 2. Parámetros de dispersión: rango, varianza, desviación típica. 3. Utilización conxunta de media e desviación típica. 4. Medidas de posición non central: cuartís, decís, percentís.

1. Parámetros de Centralización Este tipo de parámetros proporciónannos uns valores en torno ós que se centran os datos da distribución. Os principais son: Ø Media aritmética Ø Mediana Ø Moda

1. Parámetros de Centralización Veremos tamén: – – – media aritmética ponderada media a. Recortada media a. truncada ou Winsorizada, media cuadrática media xeométrica media harmónica.

1. Parámetros de Centralización. Tipos de media. Ø Media aritmética A media aritmética dunha variable estatística é o cociente entre a suma de todos os valores de dita variable e o número destes. Fórmula para datos agrupados nunha táboa estatística: xi = valor da variable ou marca de clase fi = frecuencia absoluta N = nº de datos

1. Parámetros de Centralización. Tipos de media. Ø Media aritmética ponderada: Emprégase para calcular o promedio duns valores cando estes teñen diferentes ponderacións ou pesos. Se unha variable estatística toma valores x 1, x 2, …, xn con pesos w 1, w 2, …, wn respectivamente defínese a media aritmética ponderada como:

1. Parámetros de Centralización. Tipos de media. Ø Media recortada R(p) Se temos unha serie de n datos ordenados, X 1, X 2, …, Xn, defínese a media recortada nunha porcentaxe p como a media aritmética deses datos onde se suprimen en ambos os extremos os correspondentes á porcentaxe p. Se suprimimos a datos por ambos extremos, teremos que a media recortada ó p% é:

1. Parámetros de Centralización. Tipos de media. Ø Media truncada ou Winsorizada W(p): Se temos unha serie de n datos ordenados, X 1, X 2, …, Xn, defínese a media truncada ou Winsorizada nunha porcentaxe p como a media aritmética deses datos onde se substitúen en ambos os extremos os datos correspondentes á porcentaxe p polo máis preto dese extremo.

1. Parámetros de Centralización. Tipos de media. Ø Media cuadrática Emprégase cando a variable toma valores positivos e negativos e non queremos que a medida de tendencia central reflicta os efectos do signo. É moi práctica cando traballamos con erros na medida dunha magnitude. Desígnase por C e a súa expresión para datos agrupados é: xi = valor da variable ou marca de clase fi = frecuencia absoluta N = nº de datos

1. Parámetros de Centralización. Tipos de media. ØMedia Xeométrica: Utilízase cando calculamos números índices sintéticos (combinan unha grande cantidade de prezos e producións, como o IPC). Non se pode usar cando hai valores negativos. Desígnase por G, e a súa expresión para datos agrupados é: xi = valor da variable ou marca de clase fi = frecuencia absoluta N = nº de datos

1. Parámetros de Centralización. Tipos de media. ØMedia Harmónica: É a inversa da media aritmética dos inversos dos valores da variable. É útil na comparación de velocidades promedio sobre varias distancias e na resolución de problemas estatísticos de transporte. Designase por H, e a súa fórmula para datos agrupados é: xi = valor da variable ou marca de clase fi = frecuencia absoluta N = nº de datos

1. Parámetros de Centralización. Tipos de media. Exemplo (media aritmética-media aritmética ponderada) Un alumno obtivo en tres exames as seguintes notas: 4 -5 -6. A nota media, se as tres tivesen a mesma importancia sería: En cambio, se o profesor lle dá ás notas dos exames distintas ponderacións, por exemplo: 3 -2 -1 respectivamente, a nota media ponderada sería agora:

1. Parámetros de Centralización. Tipos de media. Exemplo (media aritmética-media harmónica) AB=120 km. A B B velocidade media=30 Km/h A velocidade media=60 Km/h Acha a velocidade media da viaxe completa: A velocidade media da viaxe sería: Este promedio correspóndese coa media harmónica: Se se considerara a media aritmética das velocidades, obteríamos: Que é incorrecto!!!

1. Parámetros de Centralización. Tipos de media. Exemplo: Dada a serie estatística: 1 - 4 - 6 - 6 - 8 - 8 - 10 - 12 - 14 - 30, imos achar a media recortada ao 10% e a media winsorizada ao 10%. MEDIA RECORTADA ao 10%: o 10% de 10 é 1 e eliminamos 1 dato por cada extremo. Calculamos a media aritmética dos 8 datos restantes: 1 4 6 6 8 8 10 12 14 30 MEDIA WINSORIZADA ao 10%: substituímos os datos extremos polos datos máis próximos a eles, e calculamos a media da serie: 4 4 6 6 8 8 10 12 14 14 Obsérvase que estes valores difiren bastante da media aritmética: debido a que hai un valor atípico: 30

1. Parámetros de Centralización. Media aritmética. Exemplo variable discreta Nunha poboación de 25 familias observouse a variable número de coches que ten a familia, e obtivéronse os seguintes datos: 012310111432211121321 Xi fi xi fi 0 2 0 1 12 12 2 7 14 3 3 9 4 1 4 N=25 39

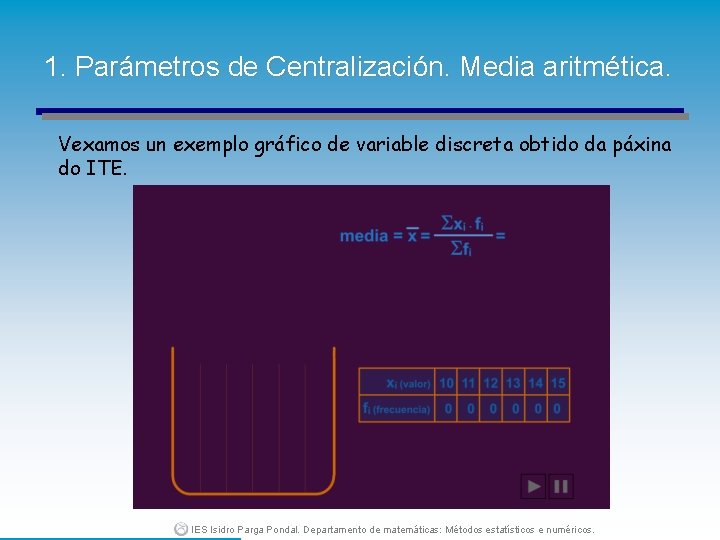
1. Parámetros de Centralización. Media aritmética. Vexamos un exemplo gráfico de variable discreta obtido da páxina do ITE. IES Isidro Parga Pondal. Departamento de matemáticas: Métodos estatísticos e numéricos.

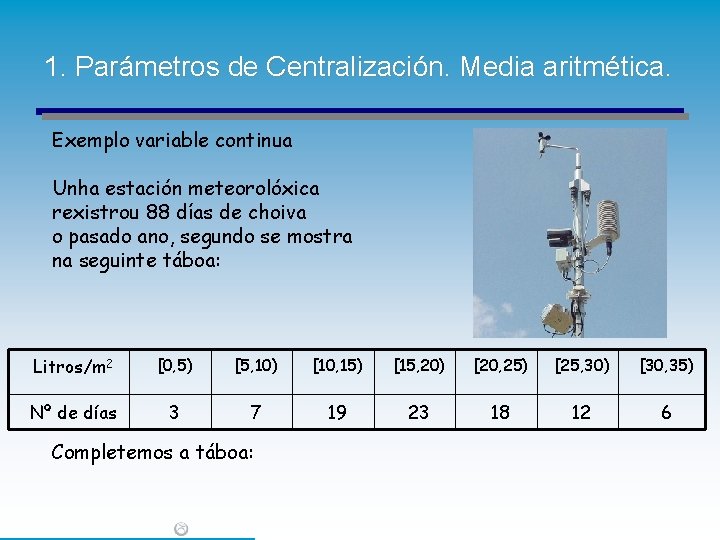
1. Parámetros de Centralización. Media aritmética. Exemplo variable continua Unha estación meteorolóxica rexistrou 88 días de choiva o pasado ano, segundo se mostra na seguinte táboa: Litros/m 2 [0, 5) [5, 10) [10, 15) [15, 20) [20, 25) [25, 30) [30, 35) Nº de días 3 7 19 23 18 12 6 Completemos a táboa:

1. Parámetros de Centralización. Media aritmética. IES Isidro Parga Pondal. Departamento de matemáticas: Métodos estatísticos e numéricos.

1. Parámetros de Centralización. Media aritmética. Litros/m 2 Marcas (xi) fi xi fi [0, 5) 2, 5 3 7, 5 [5, 10) 7, 5 7 52, 5 [10, 15) 12, 5 19 237, 5 [15, 20) 17, 5 23 402, 5 [20, 25) 22, 5 18 405 [25, 30) 27, 5 12 330 [30, 35) 32, 5 6 195 N=88 1630

1. -Parámetros de centralización: Mediana. A mediana Me dunha variable estatística é o valor de dita variable tal que o número de valores menores ca el é igual ó número de valores maiores ca el. Ou dito doutro xeito, é o valor tal que, ordenados os valores en orde crecente ou decrecente ocupa a posición central.

1. Parámetros de Centralización. Mediana. • Cálculo da mediana nas variables discretas: Se N é impar e os datos son simples a Mediana é o valor que ocupa o lugar (N+1)/2. Exemplo: 1, 4, 6, 7, 8, 10, 13, 16, 20, 24, 25, 27, 30 N=13 ocupa a posición central Me=13 Se N é par e os datos son simples hai dous valores centrais e a mediana será a media aritmética dos valores que ocupan os postos N/2 e N/2 + 1. Exemplo: 1, 4, 6, 7, 8, 10, 13, 16, 20, 24, 25, 27 N=12 ocupan as posicións centrais

1. Parámetros de Centralización. Mediana. • Cálculo da mediana nas variables discretas: Se os datos están tabulados nunha táboa de frecuencias, a mediana é o primeiro valor da variable estatística no que a frecuencia absoluta acumulada supere a metade dos datos. Se a metade dos datos coincide con algunha frecuencia absoluta acumulada , a mediana sería a media aritmética dese valor e o seguinte na táboa.

1. Parámetros de Centralización. Mediana • Cálculo da mediana nas variables continuas (ou para datos agrupados): Intervalo mediano ou clase mediana [Li-1, Li]: O primeiro no que a frecuencia absoluta acumulada supere a metade dos datos Mediana: Li-1=límite inferior da clase mediana Fi-1=frecuencia absoluta acumulada da clase anterior a mediana. fi=frecuencia absoluta da clase mediana N=nº de datos ei=lonxitude das clases ou intervalos

1. Parámetros de Centralización. Mediana. Exemplo variable discreta Voltamos ao exemplo de nº de coches por familia: -Completamos a táboa calculando as Fi N=25 impar (N+1)/2 = 26/2= 13 - Observamos cal é a primeira frecuencia absoluta acumulada que supera este valor e correspóndese co xi = 1. Por tanto, mediana=1 xi fi Fi 0 2 2 1 1 2 1 4 2 7 2 1 3 3 2 4 4 1 2 5 2 5

1. Parámetros de Centralización. Mediana. Exemplo variable continua Voltando ao exemplo da estación meterolóxica: O intervalo mediano é [15, 20) A mediana calcúlase: Li-1=15 Fi-1=29 fi=23 ei=5 Litros/m 2 Marca s (xi) fi Fi [0, 5) 2, 5 3 3 [5, 10) 7, 5 7 10 [10, 15) 12, 5 19 29 [15, 20) 17, 5 23 52 [20, 25) 22, 5 18 70 [25, 30) 27, 5 12 82 [30, 35) 32, 5 6 88 N=88

1. -Parámetros de centralización. Moda A moda dunha variable estatística, Mo , é o valor (ou valores) de dita variable que ten maior frecuencia absoluta. • Cálculo da moda nas variables discretas: O valor , ou valores, da variable estatística no que a frecuencia absoluta sexa maior.

1. Parámetros de Centralización. Moda • Cálculo da moda nas Variables continuas (ou para datos agrupados): – – Intervalo modal ou clase modal [Li-1, Li]: O intervalo no que a frecuencia absoluta sexa maior. Moda: ü ü Li-1=límite inferior da clase modal fi, fi-1, fi+1=frecuencia absoluta da clase modal, anterior e posterior D 1 =fi -fi-1 D 2 = fi –fi+1 ei=lonxitude das clases ou intervalos

1. Parámetros de Centralización. Moda. Exemplo 1 (variable discreta): Voltamos ao exemplo de nº de coches por familia: O valor da variable estatística no que a frecuencia absoluta é maior correspóndese co xi = 1. Por tanto, moda=1 xi fi Fi 0 2 2 1 12 14 2 7 21 3 3 24 4 1 25 25

1. Parámetros de Centralización. Moda. Exemplo 2 (variable continua): Litros/m 2 fi Voltando ao exemplo da estación meterolóxica: Marcas (xi) [0, 5) 2, 5 3 [5, 10) 7, 5 7 [10, 15) 12, 5 19 [15, 20) 17, 5 23 [20, 25) 22, 5 18 [25, 30) 27, 5 12 [30, 35) 32, 5 6 O intervalo modal é [15, 20) A mediana calcúlase: Li-1=15 D 1=fi-fi-1=23 -19=4 D 2=fi-fi+1=23 -18=5 ei=5 N=88

2. Parámetros de dispersión: A parte das medidas de centralización, é necesario coñecer en que medida os datos numéricos están ou non agrupados ó redor dos valores centrais. A isto é o que chaman dispersión e os parámetros que miden estas desviacións respecto da media chámanse parámetros de dispersión. Os máis importantes son: • Rango • Desviación media • Varianza • Desviación Típica

2. Parámetros de dispersión Rango O percorrido ou rango dunha distribución é a diferenza entre o maior e o menor valor da variable estatística. Desviación media A desviación media dunha variable estatística é a media aritmética dos valores absolutos das desviacións respecto á media. xi= Valor da variable ou marca de clase fi=Frecuencia absoluta N=Nº de datos Media aritmética

2. Parámetros de dispersión Varianza A varianza dunha variable estatística é a media aritmética dos cadrados das desviacións respecto á media. xi= Valor da variable ou marca de clase N=Nº de datos fi=Frecuencia absoluta Media aritmética Desviación Típica A desviación típica é a raíz cadrada positiva da varianza.

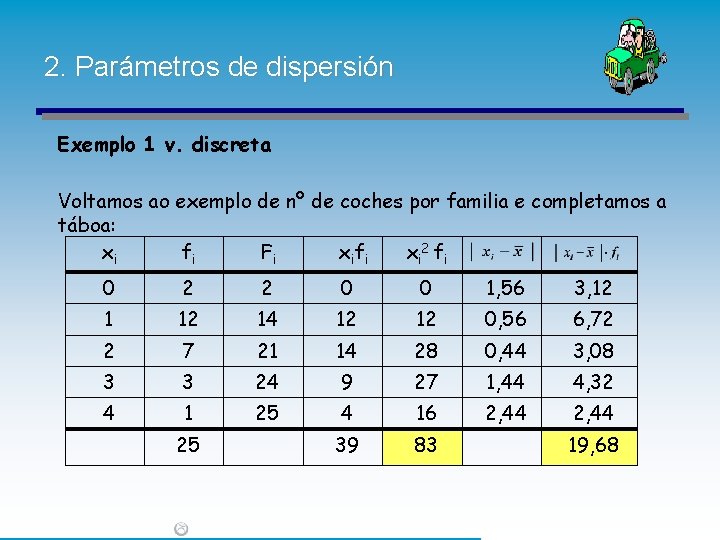
2. Parámetros de dispersión Exemplo 1 v. discreta Voltamos ao exemplo de nº de coches por familia e completamos a táboa: xi fi Fi xi fi xi 2 fi 0 2 2 0 0 1, 56 3, 12 14 12 12 0, 56 6, 72 2 7 21 14 28 0, 44 3, 08 3 3 24 9 27 1, 44 4, 32 4 1 25 4 16 2, 44 39 83 25 19, 68

2. Parámetros de dispersión Rango = 4 -0 = 4 Desviación media Varianza Desviación típica

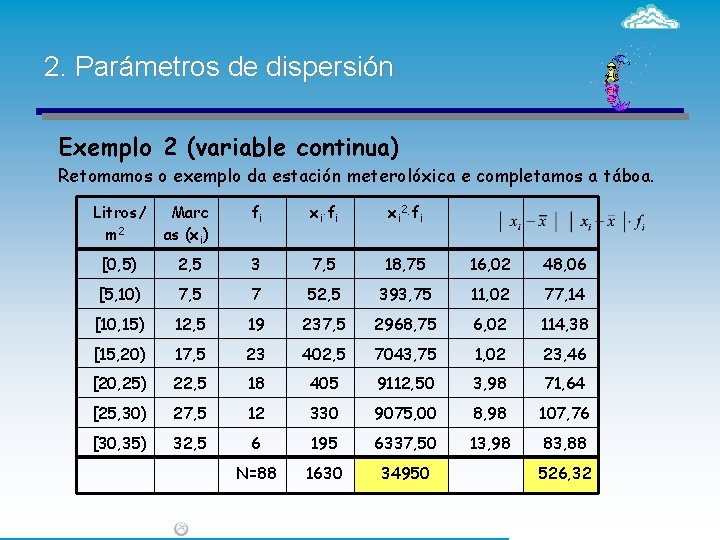
2. Parámetros de dispersión Exemplo 2 (variable continua) Retomamos o exemplo da estación meterolóxica e completamos a táboa. Litros/ m 2 Marc as (xi) fi xi 2 fi [0, 5) 2, 5 3 7, 5 18, 75 16, 02 48, 06 [5, 10) 7, 5 7 52, 5 393, 75 11, 02 77, 14 [10, 15) 12, 5 19 237, 5 2968, 75 6, 02 114, 38 [15, 20) 17, 5 23 402, 5 7043, 75 1, 02 23, 46 [20, 25) 22, 5 18 405 9112, 50 3, 98 71, 64 [25, 30) 27, 5 12 330 9075, 00 8, 98 107, 76 [30, 35) 32, 5 6 195 6337, 50 13, 98 83, 88 N=88 1630 34950 526, 32

2. Parámetros de dispersión Desviación media Varianza Desviación típica

3. Utilización conxunta de media e desviación típica. En distribucións cunha soa moda e bastante simétricas verifícase: 1. No intervalo atópase o 68% dos datos. 2. No intervalo atópase o 95% dos datos. 3. No intervalo atópase o 99% dos datos.

3. Utilización conxunta da media e a desviación típica. Exemplo Comparación media e desviación típica: coa mesma media, cal interesa ou é máis rendible? Ver Exemplo

4. Medidas de posición non central: As medidas de posición non central permiten coñecer outros puntos característicos da distribución que non son os valores centrais. Entre as medidas de posición non central máis importantes están os cuantís que son aqueles valores da variable, que ordenados de menor a maior, dividen a distribución en partes, de tal xeito que cada unha delas contén o mesmo número de frecuencias. Os tipos máis importantes de cuantís son: – Os cuartís, que dividen a distribución en catro partes; – Os decís, que dividen a distribución en dez partes; – Os percentís, que dividen a distribución en cen partes.

4. - Medidas de posición non centrais: Cuartís. Ordenados os datos en orde crecente, os cuartís Q 1, Q 2, Q 3 son os valores da variable estatística tales que a cuarta parte dos datos teñen valores inferiores a Q 1, a metade dos datos teñen valores inferiores a Q 2, e as tres cuartas partes teñen valores inferiores a Q 3. A mediana coincide con Q 2.

4. Medidas de posición. Cuartís Cálculo dos cuartis nas variables discretas: Q 1 calcúlase buscando o primeiro valor da variable no que a frecuencia absoluta acumulada supere a cuarta parte dos datos. Q 3 calcúlase buscando o primeiro valor da variable no que a frecuencia absoluta acumulada supere as tres cuartas partes dos datos.

4. Medidas de posición. Cuartís Cálculo dos cuartís nas variables continuas (ou datos agrupados): Primeiro localízanse os intervalos que conteñen os cuartís, [Li-1, Li], da mesma maneira que na variable discreta, e depois aplícase a fórmula: Li-1 = límite inferior da clase que contén o cuartil N = Nº de datos fi = Frecuencia absoluta da clase que contén o cuartil Fi-1 =frecuencia absoluta acumulada da clase anterior a que contén o cuartil. ei = lonxitude do intervalo que contén cuartil

4. - Medidas de posición non centrais: Deciles Son 9 valores da variable tales que, ordenados de maneira crecente, dividen a distribución estatística en 10 partes. Cada unha de elas contén a décima parte das observacións. Represéntanse por D 1, D 2, …, D 9. D 5 =Me

4. Medidas de posición. Deciles. Cálculo dos deciles Variable discreta: Se son datos simples, calcúlanse as frecuencias absolutas acumuladas e o decil Dk será o primeiro valor da variable cuxa frecuencia absoluta acumulada exceda a K. N/10 K=1, …, 9. Variable continua (ou datos agrupados): Calcúlase o intervalo correspondente polo procedemento anterior, [Li-1, Li], e aplícase a fórmula: K=1, 2, …, 9

4. - Medidas de posición non centrais: Percentís: Son 99 valores da variable tales que, ordenados de maneira crecente, dividen a distribución estatística en 100 partes. Cada unha delas contén a centésima parte das observacións. Representanse coa letra P. É o percentil i-ésimo, onde a i toma valores do 1 ó 99. O i% da mostra son valores menores ca el e o 100 -i% restante son maiores. P 50=Q 2=Me P 25=Q 1 P 75=Q 3

4. Medidas de posición. Percentís. Cálculo dos percentís: Variable discreta: Se son datos simples, calcúlanse as frecuencias absolutas acumuladas e o percentil Pk será o primeiro valor da variable cuxa frecuencia absoluta acumulada exceda a K. N/100 K=1, …, 99. Variable continua (ou datos agrupados): Calcúlase o intervalo correspondente polo procedemento anterior, [Li-1, Li], e aplícase a fórmula: K=1, 2, …, 99

4. Medidas de posición. Cuantís. Exemplo variable discreta Táboa dunha serie de datos referidos ó talle dun grupo de alumnos: Ver exemplo Neste exemplo só veñen calculados os cuartís: Q 1= 1, 22 cm (primeiro valor cuxa frecuencia absoluta supera o 25%) Q 2= 1, 26 cm (primeiro valor cuxa frecuencia absoluta supera o 50%) Q 3= 1, 28 cm (primeiro valor cuxa frecuencia absoluta supera o 75%)

4. Medidas de posición. Cuantís. Do mesmo modo calcúlanse os decís: D 1 será o primeiro valor cuxa frecuencia absoluta acumulada supere o 10% dos datos, o D 2 será o correspondente ao primeiro que supere o 20%, … Por exemplo: D 1=1, 22 D 5=1, 26 D 7= 1, 28 Do mesmo xeito calculariamos os percentís: Pi será o primeiro valor cuxa frecuencia absoluta acumulada supere o i% dos datos, así, se queremos coñecer o valor do P 35, observamos as frecuencias absolutas acumuladas, e o primeiro que supera este valor é: P 35= 1, 23 Outros: P 71= 1, 28 P 13= 1, 21

4. Medidas de posición. Cuantís. Exemplo variable continua Ver exemplo E clica no punto 4: “Exemplos de cálculo”

4. Medidas de posición. Cuantís. Calcular cuartís gráficamente. Nota: exemplo tomado do banco de imaxes do ITE. IES Isidro Parga Pondal. Departamento de matemáticas: Métodos estatísticos e numéricos.