MTH 426 Introduction to Measure Theory By Dr

MTH 426 Introduction to Measure Theory By Dr. Saqib Hussain 1

MTH 426 Lecture # 32 Review 2

Set A set is any well-defined list, collection, or class of objects. Examples: 3
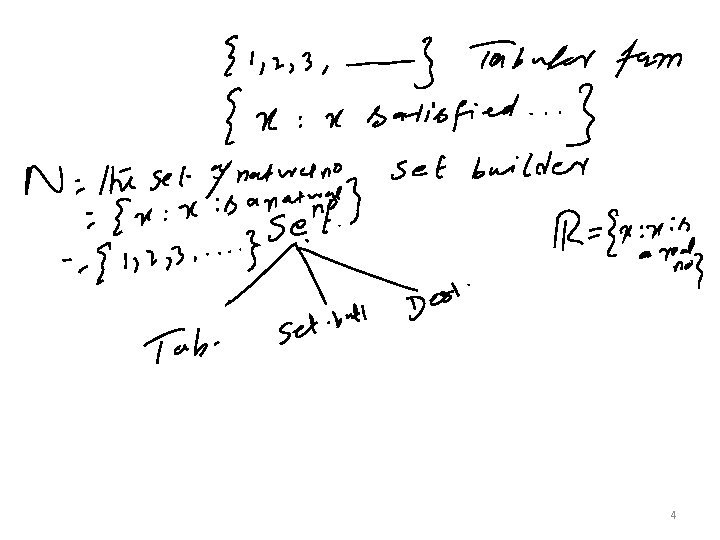
4
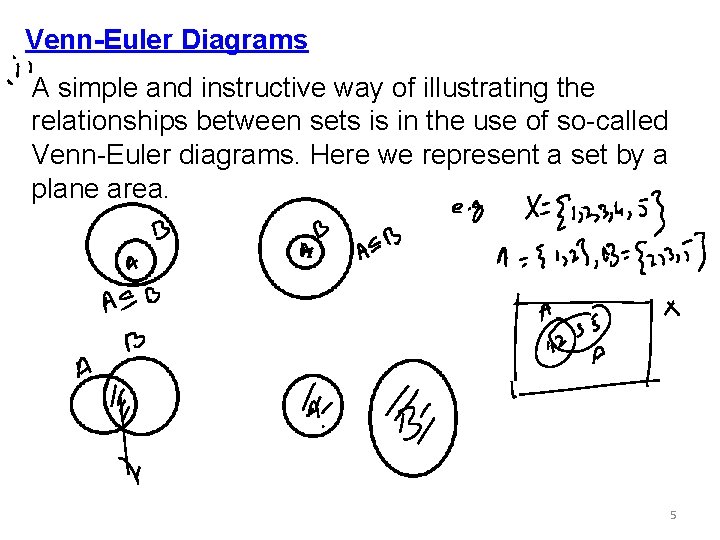
Venn-Euler Diagrams A simple and instructive way of illustrating the relationships between sets is in the use of so-called Venn-Euler diagrams. Here we represent a set by a plane area, 5
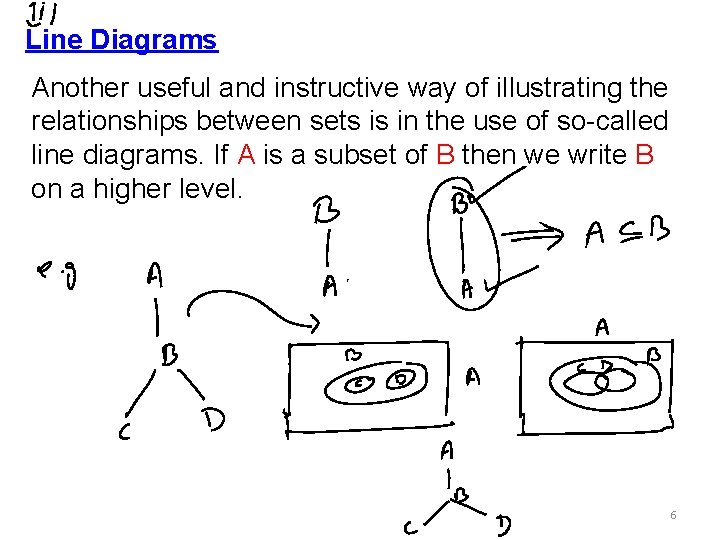
Line Diagrams Another useful and instructive way of illustrating the relationships between sets is in the use of so-called line diagrams. If A is a subset of B then we write B on a higher level. 6

Function Suppose that to each element in a set A there is assigned, by some manner or the other a unique element of a set B. We call such assignment a function. If we let f denote these assignments, then we write f: A->B 7

Relations A relation R consists of the following • a set A • a set B • An open sentence P(x, y) in which P(a, b) is true or false. We call R a relation from A to B and denote it by R=(A, B, P(a, b)) Notations: If P(a, b) is true we write a. Rb and if P(a, b) is false then we write a. Rb 8

Equivalence Relation A relation R in A is called an equivalence relation if a) R is reflexive b) R is symmetric c) R is transitive 9

Equivalent Sets Set A is equivalent to set B if there exists a function f: A->B which is both one-one and onto. Example: Let A={1, 2, 3} and B={a, b, c}. Then A B. 10

Infinite Set A set is said to be an infinite set if it is equivalent to a proper subset of itself. Example: The set of real number is an infinite set. 11

Denumerable sets Set D is said to be denumerable if it is equivalent to the set of natural number N. 12

Countable set A set is said to be countable if it is either finite or denumerable. Examples: 13

Cardinal Number Cardinality of finite and infinite sets 14

Properties 15

Exponent of cardinal numbers: 16

Continuum Hypothesis: Remark 17

Partial order relation: A relation R on a set X is said to be partial order relation if it is • reflexive, • anti-symmetric • transitive. 18

Total order relation: A partial order on a set X is said to be total order if for a, b in X either a precedes b or b precedes a. 19

Definitions: 20

Similar Sets: 21

Ordinal Numbers: Cardinal number of a well ordered set is called its ordinal number. 22

Ring of sets: Algebra of sets: 23

Definitions: 24

Measure: 25

Outer measure: 26
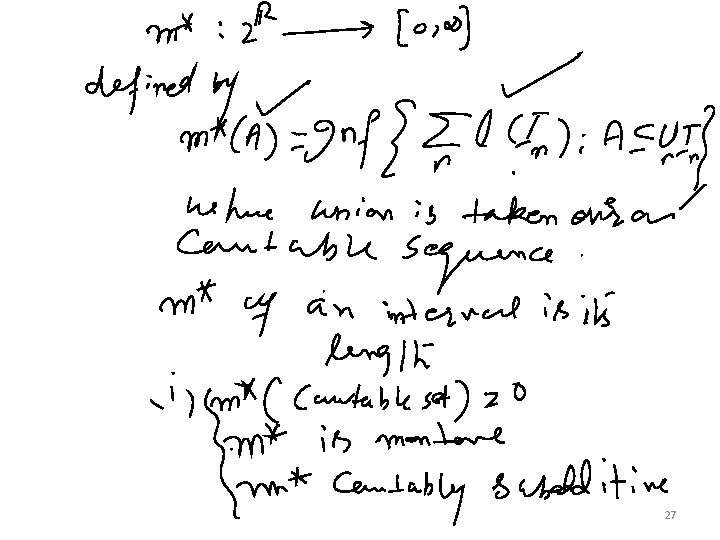
27
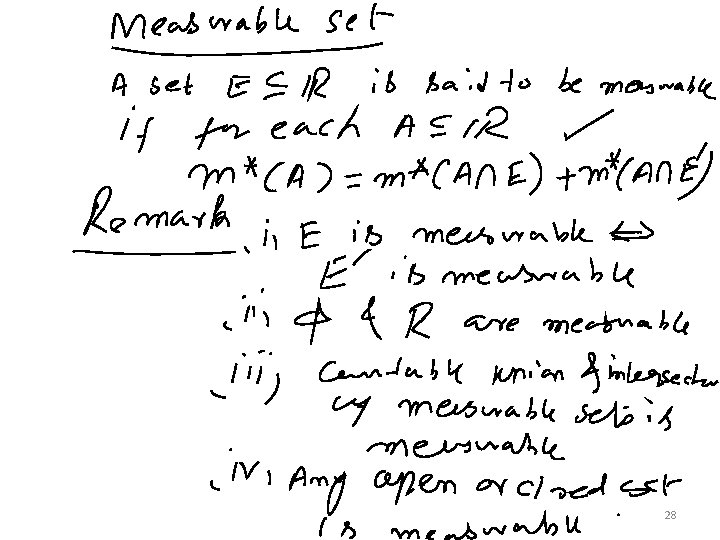
28
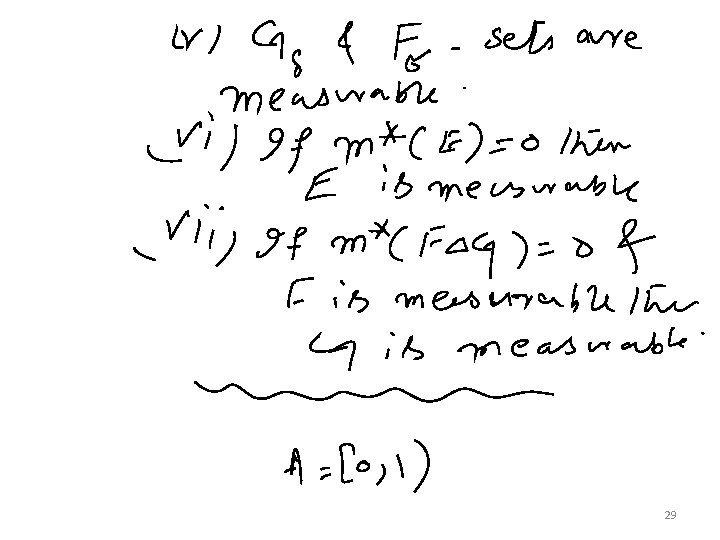
29
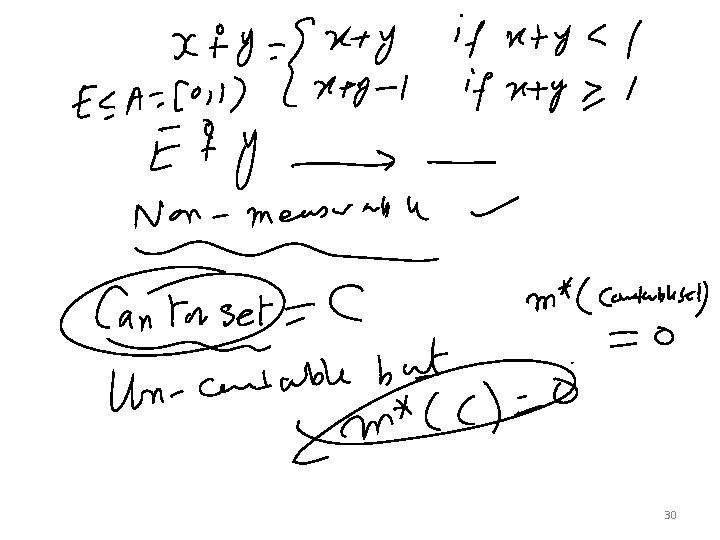
30
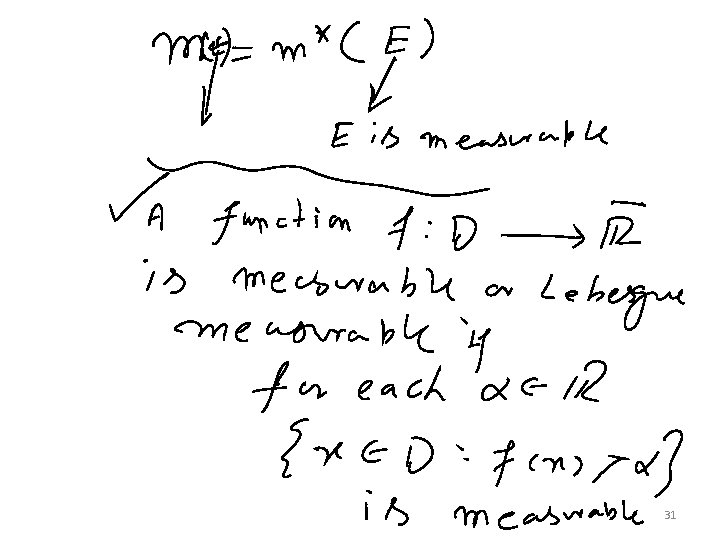
31

References: 1. Set Theory and Related Topics by Seymour Lipschutz. 2. Elements of Set Theory by Herbert B. Enderton 32
- Slides: 32