MTH 209 Week 3 Thir d Due for

MTH 209 Week 3 Thir d

Due for this week… § § § Homework 3 (on My. Math. Lab – via the Materials Link) The fifth night after class at 11: 59 pm. Read Chapter 6. 6, 8. 4 and 11. 1 -11. 5 Do the My. Math. Lab Self-Check for week 3. Learning team hardest problem assignment. Complete the Week 3 study plan after submitting week 3 homework. Participate in the Chat Discussions in the OLS Copyright © 2009 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2

Section 7. 1 Introduction to Rational Expressions Copyright © 2013, 2009, and 2005 Pearson Education, Inc.

Objectives • Basic Concepts • Simplifying Rational Expressions • Applications

Basic Concepts Rational expressions can be written as quotients (fractions) of two polynomials. Examples include:

Example If possible, evaluate each expression for the given value of the variable. a. b. c. Solution a. b. c. Try Q 7, 11, 13, 17 pg. 427

Example Try Q 25, 27, 31, 33 pg. 428 Find all values of the variable for which each expression is undefined. a. b. c. Solution a. Undefined when x 2 = 0 or when x = 0. b. Undefined when w – 4 = 0 or when w = 4. c. Undefined when w 2 – 4 = 0 or when w = 2.

Example Try Q 39, 43 pg. 428 Simplify each fraction by applying the basic principle of fractions. a. b. c. Solution a. The GCF of 9 and 15 is 3. b. The GCF of 20 and 28 is 4. c. The GCF of 45 and 135 is 45.

Example Simplify each expression. a. b. c. Solution a. c. b.

Example Try Q 51, 55, 61, 79 pg. 428 Simplify each expression. a. b. Solution a. b.

Example Try Q 105 pg. 429 Suppose that n balls, numbered 1 to n, are placed in a container and two balls have the winning number. a. What is the probability of drawing the winning ball at random? b. Calculate this probability for n = 100, 1000 and 10, 000. c. What happens to the probability of drawing the winning ball as the number of balls increases? Solution a. There are 2 chances of drawing the winning ball.

Example (cont) Try Q 105 pg. 429 b. Calculate this probability for n = 100, 1000 and 10, 000. c. What happens to the probability of drawing the winning ball as the number of balls increases? The probability decreases.

Section 7. 2 Multiplication and Division of Rational Expressions Copyright © 2013, 2009, and 2005 Pearson Education, Inc.

Objectives • Review of Multiplication and Division of Fractions • Multiplication of Rational Expressions • Division of Rational Expressions

Example Try Q 5, 7, 9 pg. 435 Multiply and simplify your answers to lowest terms. a. b. c. Solution a. b. c.

Example Try Q 13, 15, 17 pg. 435 Divide and simplify your answers to lowest terms. a. b. c. Solution a. c. b.

Example Multiply and simplify to lowest terms. Leave your answers in factored form. a. b. Solution a. b.

Example Try Q 29, 31, 45 pg. 435 Multiply and simplify to lowest terms. Leave your answer in factored form. Solution

Example Try Q 49, 57, 65 pg. 435 Divide and simplify to lowest terms. a. b. Solution a. b.

Section 7. 3 Addition and Subtraction with Like Denominators Copyright © 2013, 2009, and 2005 Pearson Education, Inc.

Objectives • Review of Addition and Subtraction of Fractions • Rational Expressions Having Like Denominators

Example Simplify each expression to lowest terms. a. b. Solution a. b.

Example Try Q 7, 9, 11, 13 pg. 442 Simplify each expression to lowest terms. a. b. Solution a. b.

SUMS OF RATIONAL EXPRESSIONS To add two rational expressions having like denominators, add their numerators. Keep the same denominator. C is nonzero

Example Try Q 19, 25, 33, 35 pg. 442 Add and simplify to lowest terms. a. b. Solution a. b.

Example Try Q 51, 53, 55 pg. 443 Add and simplify to lowest terms. a. b. Solution a. b.

DIFFERENCES OF RATIONAL EXPRESSIONS To subtract two rational expressions having like denominators, subtract their numerators. Keep the same denominator. C is nonzero

Example Try Q 21, 27, 67 pg. 442 -3 Subtract and simplify to lowest terms. a. b. Solution a. b.

Example Try Q 31, 59 pg. 442 -3 Subtract and simplify to lowest terms. Solution

Section 7. 4 Addition and Subtraction with Unlike Denominators Copyright © 2013, 2009, and 2005 Pearson Education, Inc.

Objectives • Finding Least Common Multiples • Review of Fractions Having Unlike Denominators • Rational Expressions Having Unlike Denominators

FINDING THE LEAST COMMON MULTIPLE The least common multiple (LCM) of two or more polynomials can be found as follows. Step 1: Factor each polynomial completely. Step 2: List each factor the greatest number of times that it occurs in either factorization. Step 3: Find the product of this list of factors. The result is the LCM.

Example Find the least common multiple of each pair of expressions. a. 6 x, 9 x 4 b. x 2 + 7 x + 12, x 2 + 8 x + 16 Solution Step 1: Factor each polynomial completely. 6 x = 3 ∙ 2 ∙ x 9 x 4 = 3 ∙ x ∙ x ∙ x Step 2: List each factor the greatest number of times. 3∙ 3∙ 2∙x∙x Step 3: The LCM is 18 x 4.

Example (cont)Try Q 15, 19, 27, 29 pg. 451 b. x 2 + 7 x + 12, x 2 + 8 x + 16 Step 1: Factor each polynomial completely. x 2 + 7 x + 12 = (x + 3)(x + 4) x 2 + 8 x + 16 = (x+ 4)(x + 4) Step 2: List each factor the greatest number of times. (x + 3), (x + 4), and (x + 4) Step 3: The LCM is (x + 3)(x + 4)2.

Example Try Q 45, 47 pg. 452 Simplify each expression. a. b. Solution a. The LCD is the LCM, 42. b. The LCD is 60.

Example Try Q 53, 65, 71 pg. 452 Find each sum and leave your answer in factored form. a. b. Solution a. The LCD is x 2. b.

Example Simply the expression. Write your answer in lowest terms and leave it in factored form. Solution The LCD is x(x + 7).

Example Try Q 63, 77, 79, 81 pg. 452 Simplify the expression. Write your answer in lowest terms and leave it in factored form. Solution

Example Add Try Q 101 pg. 453 and then find the reciprocal of the result. Solution The LCD is RS. The reciprocal is

Section 7. 6 Rational Equations and Formulas Copyright © 2013, 2009, and 2005 Pearson Education, Inc.

Objectives • Solving Rational Equations • Rational Expressions and Equations • Graphical and Numerical Solutions • Solving a Formula for a Variable • Applications

Rational Equations If an equation contains one or more rational expressions, it is called a rational equation.

Example Try Q 9, 15, 31, 41 pg. 473 Solve each equation. a. b. Solution a. b. The solutions are The solution is

Example Determine whether you are given an expression or an equation. If it is an expression, simplify it and then evaluate it for x = 4. If it is an equation, solve it. a. b. Solution a. There is an equal sign, so it is an equation. The answer checks. The solution is − 4.

Example (cont) b. There is no equals sign, so it is an expression. The common denominator is x – 2, so we can add the numerators. When x = 4, the expression evaluates 4 + 5 = 9. Try Q 49, 55 pg. 473

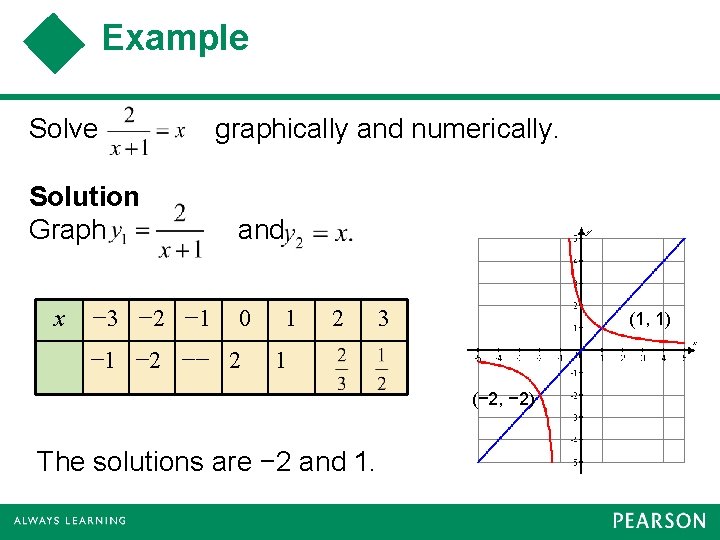
Example Solve Solution Graph x − 3 − 2 − 1 graphically and numerically. and 0 − 1 − 2 −− 2 1 2 3 (1, 1) 1 (− 2, − 2) The solutions are − 2 and 1.

Example (cont) Solve Try Q 75 pg. 474 graphically and numerically. Solution Numerical Solution x − 3 − 2 − 1 − 2 −− 0 2 1 1 2 3 − 2 − 1 0 1 2 3 The solutions are − 2 and 1.

Example Solve the equation for the specified variable. Solution

Example Solve the equation for the specified variable. Solution

Example Try Q 89, 91, 97 pg. 474 Solve the equation for the specified variable. Solution

Example Try Q 102 pg. 474 A pump can fill a swimming pool ¾ full in 6 hours, another can fill the pool ¾ full in 9 hours. How long would it take the pumps to fill the pool ¾ full, working together? Solution The two pumps can fill the pool ¾ full in hours.

Section 7. 7 Proportions and Variation Copyright © 2013, 2009, and 2005 Pearson Education, Inc.

Objectives • Proportions • Direct Variation • Inverse Variation • Analyzing Data • Joint Variation

Proportions A proportion is a statement (equation) that two ratios (fractions) are equal. The following property is a convenient way to solve proportions: is equivalent to provided b ≠ 0 and d ≠ 0.

Example Try Q 65 pg. 488 On an elliptical machine, Francis can burn 370 calories in 25 minutes. If he increases his work time to 30 minutes, how many calories will he burn? Solution Let x be the equivalent amount of calories. Thus, in 30 minutes, Francis will burn 444 calories.

Example Try Q 56 pg. 488 A 6 -foot tall person casts a shadow that is 8 -foot long. If a nearby tree casts a 32 -foot long shadow, estimate the height of the tree. Solution 6 ft h The triangles are similar because 8 ft 32 ft the measures of its corresponding angles are equal. Therefore corresponding sides are proportional. The tree is 24 feet tall.

Example Try Q 33 pg. 487 Let y be directly proportional to x, or vary directly with x. Suppose y = 9 when x = 6. Find y when x = 13. Solution Step 1 The general equation is y = kx. Step 2 Substitute 9 for y and 6 for x in y = kx. Solve for k. Step 3 Replace k with 9/6 in the equation y = 9 x/6. Step 4 To find y, let x = 13.

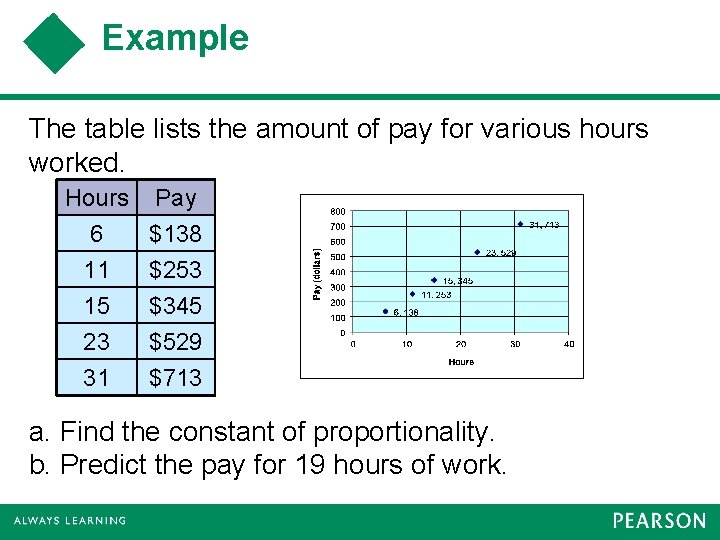
Example The table lists the amount of pay for various hours worked. Hours Pay 6 $138 11 $253 15 $345 23 31 $529 $713 a. Find the constant of proportionality. b. Predict the pay for 19 hours of work.

Example (cont) Try Q 73 pg. 488 The slope of the line equals the proportionality, k. If we use the first and last data points (6, 138) and (31, 713), the slope is The amount of pay per hour is $23. The graph of the line y = 23 x, models the given graph. To find the pay for 19 hours, substitute 19 for x. y = 23 x, y = 23(19) 19 hours of work would pay $437. 00 y = 437

Example Try Q 39 pg. 487 Let y be inversely proportional to x, or vary inversely with x. Suppose y = 6 when x = 4. Find y when x = 8. Solution Step 1 The general equation is y = k/x. Step 2 Substitute 6 for y and 4 for x in Solve for k. Step 3 Replace k with 24 in the equation y = k/x. Step 4 To find y, let x = 8.

Example Try Q 51 a, 53 a, 55 a pg. 487 -488 Determine whether the data in each table represent direct variation, inverse variation, or neither. For direct and inverse variation, find the equation. Neither the product xy nor the ratio y/x a. x 3 7 9 12 b. c. y 12 28 32 48 x y 5 12 10 6 12 5 15 4 x y 8 48 11 66 14 84 21 126 are constant in the data in the table. Therefore there is neither direct variation nor indirect variation in this table. As x increases, y decreases. Because xy = 60 for each data point, the equation y = 60/x models the data. This represents an inverse variation. The equation y = 6 x models the data. The data represents direct variation.

JOINT VARIATION Let x, y, and z denote three quantities. Then z varies jointly with x and y if there is a nonzero number k such that

Example Try Q 83 pg. 488 The strength S of a rectangular beam varies jointly as its width w and the square of its thickness t. If a beam 5 inches wide and 2 inches thick supports 280 pounds, how much can a similar beam 4 inches wide and 3 inches thick support? Solution The strength of the beam is modeled by S = kwt 2.

Example (cont) Try Q 83 pg. 488 Thus S = 14 wt 2 models the strength of this type of beam. When w = 4 and t = 3, the beam can support S = 14 ∙ 32= 504 pounds

Section 10. 1 Radical Expressions and Functions Copyright © 2013, 2009, and 2005 Pearson Education, Inc.

Objectives • Radical Notation • The Square Root Function • The Cube Root Function

Radical Notation Every positive number a has two square roots, one positive and one negative. Recall that the positive square root is called the principal square root. The symbol is called the radical sign. The expression under the radical sign is called the radicand, and an expression containing a radical sign is called a radical expression. Examples of radical expressions:

Example Try Q 15, 17, 19, 21 pg. 641 Evaluate each square root. a. b. c.

Example Approximate Solution Try Q 39 pg. 641 to the nearest thousandth.

Example Try Q 23, 25, 27, 41 pg. 641 Evaluate the cube root. a. b. c.

Example Try Q 33, 35, 37 pg. 641 Find each root, if possible. a. b. c. Solution a. b. c. An even root of a negative number is not a real number.

Example Try Q 45, 49, 51 pg. 641 Write each expression in terms of an absolute value. a. Solution a. b. c. b. c.

Example Try Q 61, 63 pg. 641 If possible, evaluate f(1) and f( 2) for each f(x). a. b. Solution a. b.

Example Try Q 75, 89 pg. 642 Calculate the hang time for a ball that is kicked 75 feet into the air. Does the hang time double when a ball is kicked twice as high? Use the formula Solution The hang time is The hang times is less than double.

Example Try Q 75, 89 pg. 641 Find the domain of each function. Write your answer in interval notation. a. b. Solution Solve 3 – 4 x 0. The domain is b. Regardless of the value of x; the expression is always positive. The function is defined for all real numbers, and it domain is

Section 10. 2 Rational Exponents Copyright © 2013, 2009, and 2005 Pearson Education, Inc.

Objectives • Basic Concepts • Properties of Rational Exponents

Example Try Q 37, 54, 59, 63 pg. 650 Write each expression in radical notation. Then evaluate the expression and round to the nearest hundredth when appropriate. a. Solution a. c. b. c. b.

Example Write each expression in radical notation. Evaluate the expression by hand when possible. a. b. Solution a. b.

Example Try Q 47, 51 pg. 650 Write each expression in radical notation. Evaluate the expression by hand when possible. a. b. Solution a. Take the fourth root of Take the fifth root of 14 b. 81 and then cube it. and then fourth it. Cannot be evaluated by hand.

Example Try Q 53, 55 pg. 650 Write each expression in radical notation and then evaluate. a. b. Solution a. b.

Example Try Q 53, 55 pg. 650 Use rational exponents to write each radical expression. a. b. c. d.

Example Write each expression using rational exponents and simplify. Write the answer with a positive exponent. Assume that all variables are positive numbers. a. b.

Example (cont) Try Q 77, 83, 91, 97 pg. 650 Write each expression using rational exponents and simplify. Write the answer with a positive exponent. Assume that all variables are positive numbers. c. d.

Example Try Q 85, 89, 95 pg. 650 Write each expression with positive rational exponents and simplify, if possible. a. b. Solution a. b.

Section 10. 3 Simplifying Radical Expressions Copyright © 2013, 2009, and 2005 Pearson Education, Inc.

Objectives • Product Rule for Radical Expressions • Quotient Rule for Radical Expressions

Product Rule for Radicals Consider the following example: Note: the product rule only works when the radicals have the same index.

Example Try Q 13, 15, 21 pg. 659 Multiply each radical expression. a. b. c.

Example Try Q 23, 51, 57, 61 pg. 659 -60 Multiply each radical expression. a. b. c.

Example Try Q 73, 75, 77, 79 pg. 660 Simplify each expression. a. b. c.

Example Try Q 45, 89, 91 pg. 660 Simplify each expression. Assume that all variables are positive. a. b. c.

Example Try Q 101, 103, 107 pg. 660 Simplify each expression. a. b.

Quotient Rule Consider the following examples of dividing radical expressions:

Example Try Q 25, 27, 29 pg. 659 Simplify each radical expression. Assume that all variables are positive. a. b.

Example Try Q 33, 39, 41 pg. 659 Simplify each radical expression. Assume that all variables are positive. a. b.

Example Try Q 95, 97 pg. 660 Simplify the radical expression. Assume that all variables are positive.

Example Simplify the expression. Solution

Example Try Q 63, 67 pg. 660 Simplify the expression. Solution

End of week 3 § § § You again have the answers to those problems not assigned Practice is SOOO important in this course. Work as much as you can with My. Math. Lab, the materials in the text, and on my Webpage. Do everything you can scrape time up for, first the hardest topics then the easiest. You are building a skill like typing, skiing, playing a game, solving puzzles.